IEWT和FSK在齒輪與滾動軸承故障診斷中的應用
向 玲, 高雪媛, 張力佳, 李媛媛
(華北電力大學(保定)機械工程系 保定,071003)
IEWT和FSK在齒輪與滾動軸承故障診斷中的應用
向 玲, 高雪媛, 張力佳, 李媛媛
(華北電力大學(保定)機械工程系 保定,071003)
改進的經(jīng)驗小波變換方法(improved empirical wavelet transform,簡稱IEWT)是一種新的自適應性信號處理方法,將這種方法和快速譜峭度(fast spectral kurtosis,簡稱FSK)相結合,進行齒輪與滾動軸承的故障診斷。首先,采用IEWT對信號進行分解,篩選出故障特征最為明顯的2個分量并重構信號;其次,對重構信號進行快速譜峭度濾波;最后,對濾波后的信號進行包絡譜分析,提取出信號的故障特征。分析齒輪斷齒及滾動軸承故障信號,與直接包絡譜和基于EMD經(jīng)驗模態(tài)分解(empirical mode decomposition,簡稱EMD)方法的FSK濾波包絡譜分析方法相比可知,采用IEWT處理后再進行FSK濾波的信號進行包絡譜分析更具有區(qū)分性,可有效識別齒輪和滾動軸承的故障特征。
經(jīng)驗小波分解; 快速譜峭度濾波; 包絡譜分析; 故障診斷
引 言
齒輪和滾動軸承的故障信號均為非平穩(wěn)調(diào)制信號。共振解調(diào)技術[1]是目前最常用的齒輪、軸承故障診斷方法,該方法需要先對信號進行帶通濾波,再進行包絡譜分析。由于帶通濾波器的中心頻率選擇困難,且對分析結果影響較大,其應用受到了限制。峭度能夠敏銳地反映出瞬態(tài)沖擊成分,可作為選擇帶通濾波器中心頻率的衡量標準,但是峭度無法在強噪聲信號中檢測到瞬態(tài)沖擊成分,譜峭度[2-3]可以適應強噪聲環(huán)境,但其估計值只在平穩(wěn)狀態(tài)下是穩(wěn)定的。Antoni[4]為了解決這些問題提出快速譜峭度濾波方法,通過計算故障信號中每個頻段的譜峭度值,可以迅速找到譜峭度值最大時所對應的頻率和頻率分辨率,以此作為濾波器的中心頻率和帶寬,雖然在強噪聲環(huán)境中效果有所改善,結果仍不理想。蔣超等[5]利用EEMD和快速譜峭度,提出了一種敏感IMF選取方法。蔡艷平等[6]提出的方法解決了包絡譜分析中主觀性給結果帶來的影響,但是EMD方法仍存在諸多問題,如過包絡、欠包絡、模態(tài)混疊和端點效應等[7-9]。Gilles[10]提出一種對信號傅里葉頻譜進行自適應地劃分濾波的信號處理方法,即經(jīng)驗小波變換(empirical wavelet transform,簡稱EWT),濾波后可以得到一組單分量,該信號處理方法的計算速度快,模態(tài)混疊和端點效應減弱。為了進一步抑制模態(tài)混疊效應產(chǎn)生的負面影響,Gilles等[11]提出了EWT方法中窗函數(shù)邊界線選擇的優(yōu)化方法,但僅將該方法應用于腦電波及地震信號,并未應用到齒輪及軸承故障診斷的研究領域中。在以上研究基礎上,筆者提出一種基于IEWT和FSK濾波的診斷方法,將其應用到齒輪與滾動軸承故障實例,并與直接包絡譜和基于EMD方法的FSK濾波包絡譜分析方法進行對比。
1 改進的EWT
經(jīng)驗小波變換是一種自適應的信號處理方法。首先,規(guī)定規(guī)范化的信號傅里葉頻譜的頻率范圍為[0,π],假設將傅里葉頻譜分成N個部分,并且以ωn表示相鄰兩個區(qū)域的分界點,共需要確定N+1條分界線,其中0和π分別為第1條和最后一條分界線,那么,還需要確定其余N-1條分界線,以相鄰兩個連續(xù)極大值的中點為分界線所在點[9]。于是,最終得到傅里葉頻譜分界點為

(1≤n≤N-1;ω0=0;ωN=π)
(1)
當傅里葉頻譜中的兩個分量簡單易分時,將兩個連續(xù)極大值的中點作為分界點十分簡單有效,但是當連續(xù)的兩個分量分別為緊支撐和寬支撐時,該種方法就會失效,導致分界線落在支撐較寬的分量內(nèi)部,產(chǎn)生模態(tài)混疊。Gilles[10]提出了避免該種情況出現(xiàn)的最簡單的方法,即找到兩個連續(xù)極大值之間的極小值,以該點作為兩個連續(xù)分量的分界線。如果以Ωn表示ωn-1和ωn之間的局部極小值,則
ωn=argminΩn
(1≤n≤N-1;ω0=0;ωN=π)
(2)
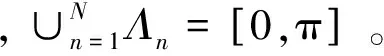
圖1 分界線示意圖Fig.1 Dividing line diagram
對分割區(qū)間Λn加小波窗,按照Meyer小波的構造方法,得到經(jīng)驗尺度函數(shù)和經(jīng)驗小波函數(shù)[10]為
F1,t(ψn)(ω)=
(3)
F1,t(φ1)(ω)=
(4)
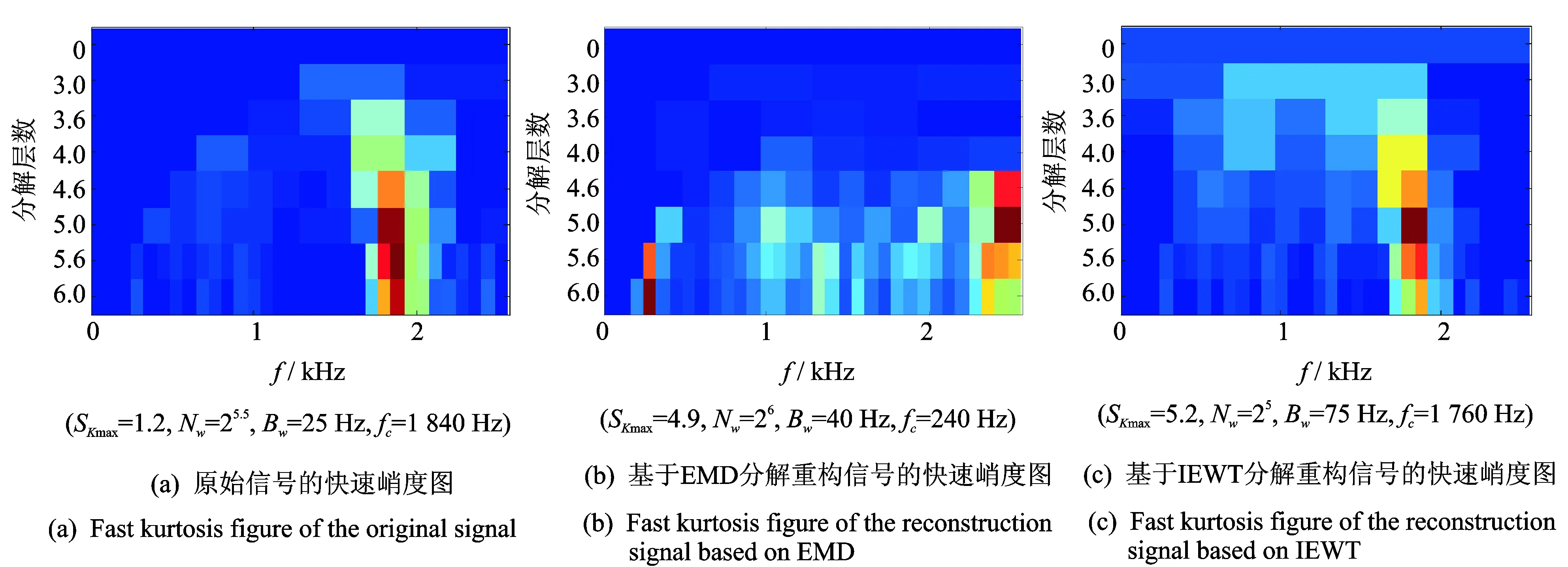
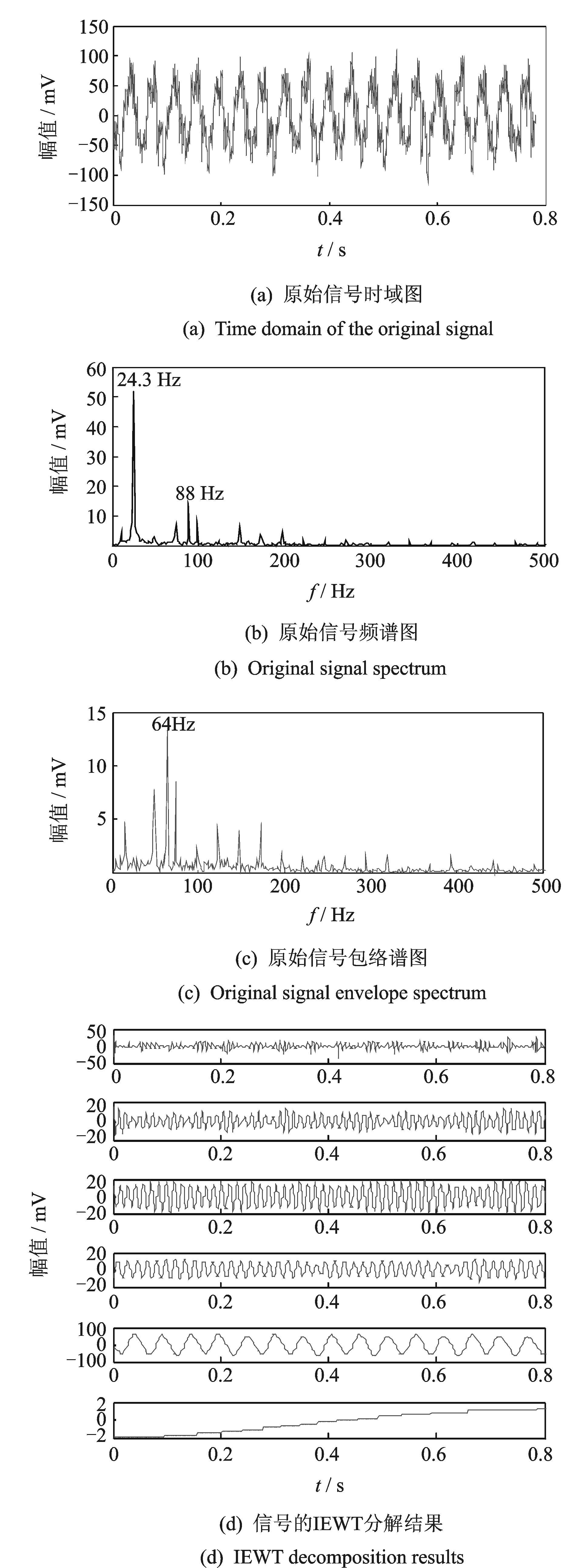
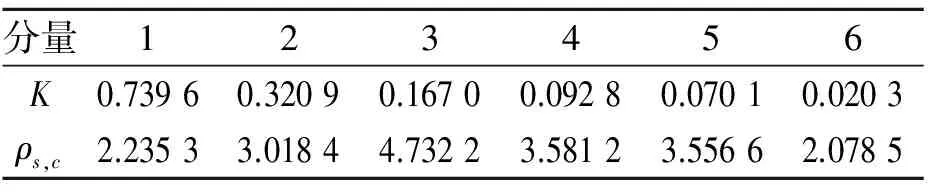
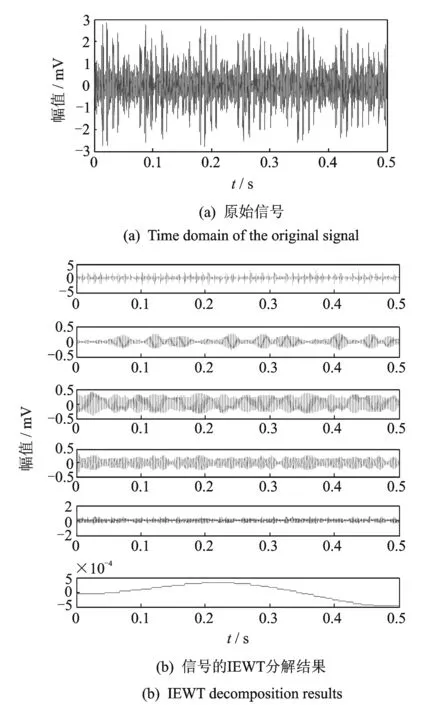
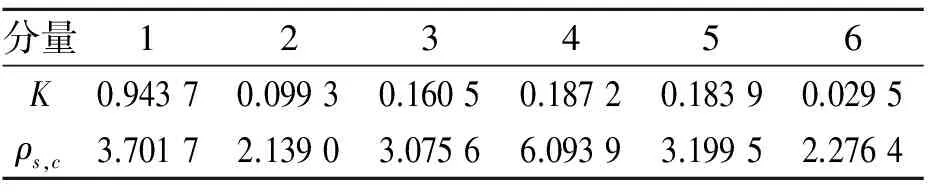
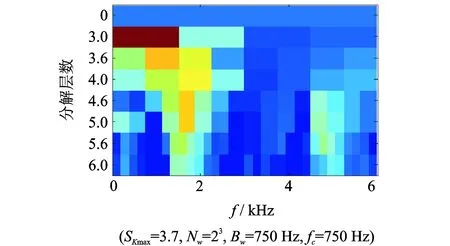
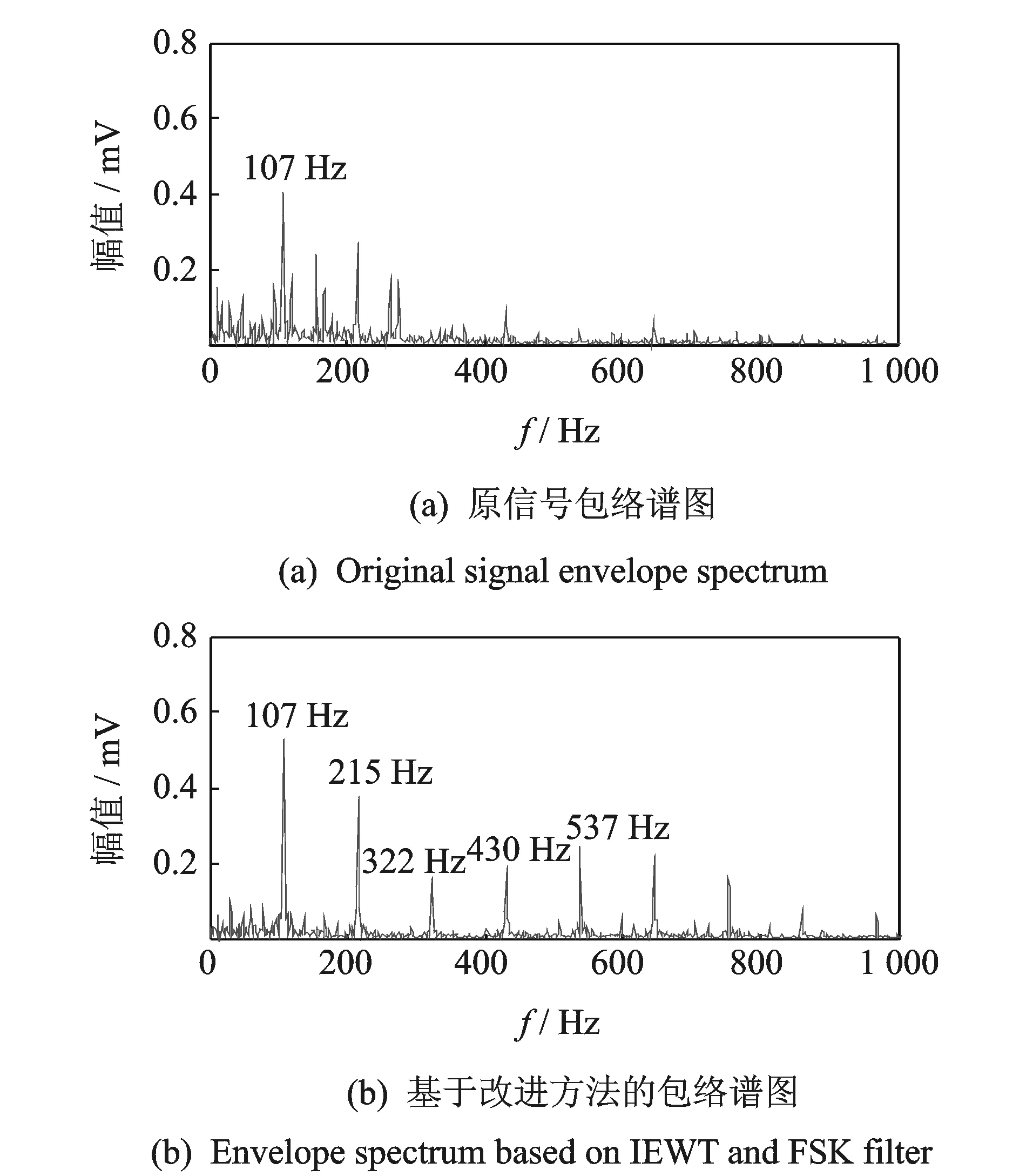
其中:γ 由經(jīng)驗小波函數(shù)內(nèi)積計算得到的細節(jié)系數(shù)以及由經(jīng)驗尺度函數(shù)的內(nèi)積計算得到的近似系數(shù)[11]分別為 (5) (6) 對信號進行重構,則重構信號[11]可以表示為 (7) 對于非平穩(wěn)信號,如何選擇最優(yōu)頻率和頻率分辨率是關鍵問題,為了解決該問題,并達到快速計算譜峭度的目的,文獻[12]提出快速峭度圖方法。該方法將信號按照每層2n個頻段進行分解,然后計算每層每個頻段的譜峭度值,譜峭度估計值是頻率f和頻率分辨率Δf的函數(shù),通過計算時頻圖上每個頻率成分的譜峭度值從而得到譜峭度值最大時對應的f和Δf,即最優(yōu)帶通濾波器中心頻率以及帶寬,其中Δf≈fs·2/Nω[13]。快速譜峭度圖如圖2所示,其橫坐標為頻率值f,縱坐標為分解層數(shù)n,圖中頻段顏色越深代表譜峭度值越大,可以方便確定譜峭度值最大時所對應的f和Δf的最優(yōu)組合。 圖2 斷齒故障快速峭度圖Fig.2 Fast kurtosis figure of broken teeth failure 譜峭度法在齒輪和軸承故障診斷應用中獲得了一定的成果,但無法適應高噪聲環(huán)境。胡愛軍等[14]提出基于集合經(jīng)驗模態(tài)分解(ensemble empirical mode decomposition,簡稱EEMD)與譜峭度準則的包絡譜分析方法,用峭度最大準則選取IMF分量進行包絡譜分解,提取出軸承故障的特征信息。蘇文勝等[15]提出基于相關系數(shù)和譜峭度準則的EMD降噪方法對信號進行預處理,更好地診斷出滾動軸承早期故障。利用上述文獻中提出的采用相關系數(shù)和譜峭度準則剔除無關分量方法,采用基于互相關系數(shù)和峭度準則的IEWT來對信號進行預處理,突出高頻共振成分,減少噪聲。基于IEWT和FSK濾波的具體診斷流程如下: 1) 對信號進行IEWT分解; 2) 計算分解后各分量的峭度值和相關系數(shù),篩選出相關系數(shù)和峭度值最大的分量重構信號; 3) 利用快速譜峭度圖方法計算得到帶通濾波器的最優(yōu)中心頻率和帶寬,然后對濾波后的信號進行包絡譜分析,以確定故障特征頻率。 QPZZ-II旋轉機械振動故障模擬實驗平臺如圖3所示,可快速模擬旋轉機械多種故障狀態(tài)。齒輪傳動比為75∶55。 圖3 QPZZ-II模擬實驗平臺Fig.3 QPZZ-II simulation experiment platform 在輸入軸的大齒輪上加工出斷齒故障,將加速度傳感器安裝在齒輪箱箱體上。其中,輸入軸轉速為1 500 r/min,斷齒故障頻率與軸的轉頻相同為25 Hz,采樣頻率為5 120 Hz。圖4給出了原信號的時域圖、頻域圖、包絡譜圖及經(jīng)IEWT分解后各分量的時域波形圖。 圖4 斷齒故障信號分析Fig.4 The signal analysis for broken teeth fault 在圖4中,斷齒故障信號的時域波形雖然有明顯的沖擊成分,但難以分辨出具體特征;頻譜圖中能看到旋轉頻率,但不存在倍頻成分等故障特征頻率;包絡譜圖中,頻率成分混亂,無法判斷齒輪發(fā)生何種故障。由式(8)和式(9)計算齒輪斷齒故障信號經(jīng)EMD和IEWT分解后各分量的峭度值和相關系數(shù),結果如表1、表2所示。 峭度值 (8) 相關系數(shù) ρs,cj=max[Rs,cj(τ)]/max[Rs(τ)] (9) 其中:x為振動信號;μ為信號x的均值;δ為信號x的標準差;Rs,cj(τ)為各分量與原始信號的互相關;Rs(τ)為原始信號的自相關。 表1EMD各分量相關系數(shù)K及峭度值ρs,c Tab.1ThecorrelationcoefficientandkurtosisvalueofeachcomponentofEMD 分量123456K0.73960.32090.16700.09280.07010.0203ρs,c2.23533.01844.73223.58123.55662.0785 表2IEWT各分量相關系數(shù)K及峭度值ρs,c Tab.2ThecorrelationcoefficientandkurtosisvalueofeachcomponentofIEWT 分量123456K0.33010.14560.23510.15920.89020.0295ρs,c3.77861.86051.65891.81011.55711.7786 由表1可知,齒輪斷齒故障信號經(jīng)EMD分解所得結果中,分量1和分量3的互相關系數(shù)和峭度值最大,沖擊特性最明顯,取這2個分量重構信號。同理,根據(jù)表2中IEWT分解結果,取分量1和分量5進行信號重構。對原信號、基于EMD方法和基于IEWT方法的重構信號進行快速譜峭度分析,得到如圖2所示的快速譜峭度圖。對比圖2各譜峭度圖可知:對于原始信號、基于EMD重構信號及基于IEWT重構信號,三者的最大譜峭度值分別為1.2,4.9和5.2,譜峭度值最大時對應的分解層數(shù)分別為5.5,6和5,濾波器中心頻率和帶寬組合分別為[1 840,25],[240,40],[1 760,75]Hz。為了突出特征頻率,分別以上述3組中心頻率和帶寬構造的濾波器對信號進行濾波,對濾波后的信號進行包絡譜分析。圖5為上述3種信號經(jīng)濾波后的包絡譜圖。 由圖5可知,原始信號包絡譜中,頻率成分混亂,不能分辨出故障特征頻率;基于EMD和快速譜峭度濾波的包絡譜分析結果中,雖然出現(xiàn)了少量的倍頻成分,但是噪聲干擾嚴重;基于IEWT和快速譜峭度濾波的包絡譜分析結果中,噪聲得到了有效抑制,故障特征頻率明顯,25,49,74和99 Hz幅值都比較突出,分別對應故障信號的轉頻及其倍頻成分,由此可以判斷該齒輪發(fā)生了故障。 軸承外圈故障信號為凱斯西儲大學軸承數(shù)據(jù)。實驗所選用軸承為SKF6205深溝球軸承,布置單點外圈故障,故障直徑為0.178 mm。其中,驅(qū)動電機轉速為1 797 r/min,采樣頻率設置為12 kHz。軸承節(jié)圓直徑為39 mm,滾動體直徑為7.9 mm,壓力角α=0°,由式(10)可計算得到軸承外圈故障頻率為107 Hz (10) 其中:d為滾動體直徑;D為軸承的節(jié)圓直徑;α為接觸角;N為滾動體個數(shù);fr為軸的轉頻。 原信號和經(jīng)IEWT分解后各分量的時域波形如圖6所示。 圖6 軸承外圈故障信號分析Fig.6 The signal analysis for outer ring fault of bearing 計算軸承外圈故障信號經(jīng)IEWT分解后各分量的峭度值和相關系數(shù),結果如表3所示。 表3各分量相關系數(shù)K及峭度值ρs,c Tab.3Thecorrelationcoefficientandkurtosisvalueofeachcomponent 分量123456K0.94370.09930.16050.18720.18390.0295ρs,c3.70172.13903.07566.09393.19952.2764 由表3可知,分量1和分量4的互相關系數(shù)及譜峭度值最大,故取這2個分量對信號進行重構。對重構的信號進行快速譜峭度分析,得到如圖7所示的快速譜峭度圖。 圖7 軸承外圈故障快速峭度圖Fig.7 Fast kurtosis figure of bearing outer ring fault 由圖7可知,重構信號的最大譜峭度值為3.7,譜峭度值最大時所對應的分解層數(shù)為3,濾波器中心頻率和帶寬組合為[750,750]Hz。以該中心頻率和帶寬構造濾波器,對信號進行濾波,再對濾波后的信號進行包絡譜分析,得到如圖8所示的原始信號包絡譜及基于IEWT和FSK濾波的信號包絡譜。 圖8 外圈故障信號包絡譜圖Fig.8 The signal envelope spectrum for outer ring fault 圖8(a)為對原始信號直接進行包絡譜分析的結果,圖中顯示故障特征頻率107 Hz明顯,但故障頻率倍頻成分的幅值較低,不易分辨。基于IEWT和FSK濾波的包絡譜分析結果中,30,107,215,322和430 Hz等頻率成分的幅值都比較突出,分別對應故障信號的轉頻、故障頻率及故障頻率的2倍頻、3倍頻及4倍頻,故障特征明顯,由此可以判斷該故障為滾動軸承外圈故障。 提出基于IEWT降噪和快速譜峭度FSK濾波的包絡譜分析方法,將IEWT方法代替?zhèn)鹘y(tǒng)的EMD方法,對信號進行分解重構,克服了EMD方法產(chǎn)生的模態(tài)混疊和端點效應,降噪效果更加突出。將該方法應用到斷齒齒輪故障和滾動軸承外圈故障的實驗模擬數(shù)據(jù)中,并對IEWT方法和EMD方法的診斷性能進行比較,結果表明,IEWT降噪和FSK濾波的包絡譜分析方法得到的包絡譜圖故障特征更加明顯,證明了該方法的有效性。 [1] 王平, 廖明夫. 滾動軸承故障診斷的自適應共振解調(diào)技術[J]. 航空動力學報, 2005,20(4):606-612. Wang Ping, Liao Mingfu. Adaptive demodulated resonance technique for the rolling bearing fault diagnosis[J]. Journal of Aerospace Power, 2005, 20(4):606-612. (in Chinese) [2] Dwyer R F. Detection of non-Gaussian signals by frequency domen Kurtosis estimation[C]∥Acoustics Speech and Signal Processing, IEEE International Conference on ICASSP.Boston:IEEE, 1983:607-610. [3] Antoni J, Randall R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines[J]. Systems and Signal Processing, 2006, 20(2):308-331. [4] Antoni J. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007, 21(1):108-124. [5] 蔣超, 劉樹林, 姜銳紅,等. 基于快速譜峭度圖的EEMD內(nèi)稟模態(tài)分量選取方法[J]. 振動、測試與診斷, 2015(6):1173-1178. Jiang Chao, Liu Shulin, Jiang Ruihong, et al. Feature extraction method of intrinsic mode function in EEMD based on fast kurtogram in machinery fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2015(6):1173-1178. (in Chinese) [6] 蔡艷平, 李艾華, 石林鎖, 等. 基于EMD與譜峭度的滾動軸承故障檢測改進包絡譜分析[J]. 振動與沖擊, 2011, 30(2):167-172,191. Cai Yanping, Li Aihua, Shi Linsuo, et al. Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock, 2011, 30(2): 167-172,191.(in Chinese) [7] Loh C H, Wu T C, Huang N E. Application of the empirical mode decomposition-Hilbert spectrum method to identify near-fault ground-motion characteristics and structural responses[J]. Bulletin of the Seismological Society of America, 2001, 91 (5): 1339-1357. [8] 孟宗, 顧海燕, 李姍姍. 基于神經(jīng)網(wǎng)絡集成的B樣條經(jīng)驗模態(tài)分解端點效應抑制方法[J]. 機械工程學報, 2013, 49(9):106-112. Meng Zong, Gu Haiyan, Li Shanshan. Restraining method for end effect of B-spline empirical mode decomposition based on neural network ensemble[J]. Journal of Mechanical Engineering, 2013,49 (9):106-112. (in Chinese) [9] 陳浩, 郭軍海, 齊巍. 基于經(jīng)驗小波變換的目標加速度估計算法[J]. 北京航空航天大學學報, 2014, 41(1):14-19. Chen Hao, Guo Junhai, Qi Wei. Estimation of target′s acceleration based on empirical wavelet transform[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 41(1):14-19. (in Chinese) [10] Gilles J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16):3999-4010. [11] Gilles J, Tran G, Osher S. 2D empirical transforms.wavelets, ridgelets and curvelets revisited[J]. Siam Journal on Imaging Sciences, 2014, 7(7):157-186. [12] Francis A, Muruganantham C. An adaptive denoising method using empirical wavelet transform[J]. International Journal of Computer Applications, 2015, 117(21):18-20. [13] 彭暢, 柏林, 謝小亮. 基于EEMD、度量因子和快速峭度圖的滾動軸承故障診斷方法[J]. 振動與沖擊, 2012, 20(31):143-146. Peng Chang, Bo Lin, Xie Xiaoliang. Fault diagnosis method of rolling element bearings based on EEMD, measure-factor and fast kurtogram[J]. Journal of Vibration and Shock, 2012, 20(31):143-146. (in Chinese) [14] 胡愛軍, 馬萬里, 唐貴基. 基于集成經(jīng)驗模態(tài)分解和峭度準則的滾動軸承故障特征提取方法[J]. 中國電機工程學報, 2012, 32(11):106-111,153. Hu Aijun, Ma Wanli, Tang Guiji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]. Proceedings of the CSEE, 2012, 32(11):106-111,153. (in Chinese) [15] 蘇文勝, 王奉濤, 張志新,等. EMD降噪和譜峭度法在滾動軸承早期故障診斷中的應用[J]. 振動與沖擊, 2010, 29(3):18-21,201. Su Wensheng, Wang Fengtao, Zhang Zhixin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock, 2010, 29(3):18-21,201. (in Chinese) 10.16450/j.cnki.issn.1004-6801.2017.06.028 國家自然科學基金資助項目(51675178,51475164) 2016-01-27; 2016-05-23 TH165.3; TN911.7 向玲,女,1971年4月生,博士、教授。主要研究方向為非線性動力學和故障診斷。曾發(fā)表《HHT方法在轉子振動故障診斷中的應用》(《中國電機工程學報》2007年第27卷第35期)等論文。 E-mail:ncepuxl@163.com2 快速譜峭度圖
3 故障診斷流程
4 試驗信號診斷方法對比
4.1 齒輪斷齒故障

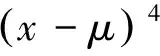

4.2 軸承外圈故障
5 結束語


