基于隱馬爾可夫模型的電力系統(tǒng)連鎖故障預(yù)測(cè)
丁巖,郭和強(qiáng),王利利,李秋燕,孫義豪,關(guān)朝杰
(1.國(guó)網(wǎng)河南省電力公司經(jīng)濟(jì)技術(shù)研究院,河南鄭州 450001;2.天津天大求實(shí)電力新技術(shù)股份有限公司,天津 300001)
基于隱馬爾可夫模型的電力系統(tǒng)連鎖故障預(yù)測(cè)
丁巖1,郭和強(qiáng)2,王利利1,李秋燕1,孫義豪1,關(guān)朝杰1
(1.國(guó)網(wǎng)河南省電力公司經(jīng)濟(jì)技術(shù)研究院,河南鄭州 450001;2.天津天大求實(shí)電力新技術(shù)股份有限公司,天津 300001)
在國(guó)民經(jīng)濟(jì)中,電力的地位異常重要,社會(huì)的發(fā)展以及電網(wǎng)的擴(kuò)大都離不開(kāi)供電的可靠性。然而,操作不當(dāng)、電網(wǎng)結(jié)構(gòu)不合理、短路(或斷路)等故障以及其他外界因素的干擾,都可能導(dǎo)致電力系統(tǒng)事故,甚至發(fā)生大面積停電[1]。因此,對(duì)電力系統(tǒng)連鎖故障的預(yù)測(cè)和診斷有助于電力系統(tǒng)可靠性的提高以及停電損失的減少[2]。一旦發(fā)生電力系統(tǒng)大事故或者大面積停電,將會(huì)給經(jīng)濟(jì)帶來(lái)重大損失,甚至給社會(huì)帶來(lái)難以預(yù)想的重大影響[3]。
隨著科技的迅速發(fā)展,電路的集成度越來(lái)越高,因此電力系統(tǒng)具有更加復(fù)雜的結(jié)構(gòu)。電力系統(tǒng)中任何一級(jí)發(fā)生故障,都會(huì)產(chǎn)生很大的影響,特別是連鎖故障的發(fā)生,影響程度會(huì)更大。雖然我們無(wú)法避免單個(gè)元件發(fā)生故障,但是,可以通過(guò)各種預(yù)測(cè)和技術(shù)手段,將連鎖故障降低到最低。目前,在國(guó)外關(guān)于連鎖故障預(yù)測(cè)的相關(guān)研究已經(jīng)很多,例如蒙特卡羅抽樣法、隨機(jī)模擬法或N-1判據(jù)等方法[4-5]。面對(duì)連鎖故障或多重故障等較難處理的情況,可以采用N-1判據(jù)法來(lái)處理;對(duì)于不確定事件,可以基于蒙特卡羅抽樣的隨機(jī)模擬來(lái)預(yù)測(cè)初始故障。
在連鎖故障預(yù)測(cè)的研究領(lǐng)域中,解決故障預(yù)測(cè)主要包括兩種方法:一是基于人工智能的方法,二是基于復(fù)雜網(wǎng)絡(luò)理論的方法。人工智能方法又可以分為不同的模型,例如OPA模型、CASCADE模型以及隱藏故障模型等,這種方法的特點(diǎn)是對(duì)電力系統(tǒng)的演化過(guò)程較為簡(jiǎn)潔,但是人工智能的故障預(yù)測(cè)還存在著不足,如果某條線路停止對(duì)狀態(tài)更新,那么這種方法對(duì)潮流等方面的模擬將會(huì)脫離實(shí)際電力系統(tǒng)的運(yùn)行狀態(tài)。隨著網(wǎng)絡(luò)理論復(fù)雜程度的不斷增加,小世界模型實(shí)現(xiàn)了對(duì)復(fù)雜網(wǎng)絡(luò)理論的連鎖故障預(yù)測(cè),這種模型主要是從網(wǎng)絡(luò)結(jié)構(gòu)角度來(lái)研究,分析當(dāng)電力網(wǎng)絡(luò)遭受各種不同攻擊時(shí),電網(wǎng)所能承受的最大限度。此外,如果電力網(wǎng)絡(luò)被攻擊,這種攻擊可能會(huì)造成連鎖故障等問(wèn)題。在連鎖故障預(yù)測(cè)方面,問(wèn)題比較復(fù)雜,常常存在著隱藏狀態(tài),為了能夠清晰地將觀測(cè)狀態(tài)與隱藏狀態(tài)的對(duì)應(yīng)關(guān)系描述出來(lái),可采用隱馬爾可夫模型。
1 隱馬爾可夫模型的基本理論
1.1 馬爾可夫鏈
在狀態(tài)空間和時(shí)間參數(shù)均為離散的條件下,馬爾可夫過(guò)程也可以稱(chēng)為馬爾可夫鏈。在馬爾可夫過(guò)程中,隨機(jī)過(guò)程的將來(lái)狀態(tài)只是與當(dāng)前狀態(tài)有關(guān),而與過(guò)去狀態(tài)無(wú)關(guān)。在數(shù)學(xué)領(lǐng)域中,馬爾可夫鏈的定義如下:
假設(shè),存在一個(gè)隨機(jī)過(guò)程X(t),t∈T,對(duì)于S1,S2,…,SN等N個(gè)互不相同的狀態(tài),其中n=1,2,…,n∈R,X(t)在t時(shí)刻可能的狀態(tài)一定是N個(gè)互不相同的狀態(tài)中的一個(gè),且X(t)只在t1,t2,…,tn個(gè)可列個(gè)時(shí)刻(即時(shí)間參數(shù)為離散的)發(fā)生狀態(tài)轉(zhuǎn)移。
馬爾可夫鏈描述了隨機(jī)過(guò)程在時(shí)間參數(shù)為離散值的條件下,隨機(jī)過(guò)程X(t)在不同時(shí)刻所對(duì)應(yīng)狀態(tài)可能發(fā)生的概率。隨機(jī)狀態(tài)發(fā)生概率如下:
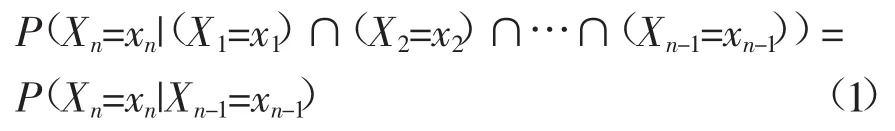
其中,將來(lái)狀態(tài)(t=n時(shí)刻)的隨機(jī)變量值Xn僅僅和當(dāng)前狀態(tài)(t=n-1時(shí)刻)的隨機(jī)變量的取值Xn-1有關(guān)。狀態(tài)i到狀態(tài)j的一步轉(zhuǎn)移概率的表達(dá)式如下:
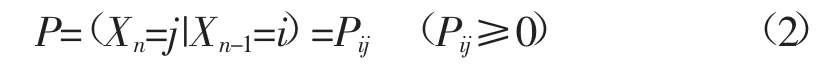
其中,當(dāng)狀態(tài)i屬于離散空間B時(shí),有:

馬爾可夫鏈具有平穩(wěn)性、周期性、互通性、普遍性以及常返性等特征。在理想情況下,每一個(gè)可以觀測(cè)到的實(shí)際存在的事件,都可以嚴(yán)格地對(duì)應(yīng)馬爾可夫鏈中的一個(gè)狀態(tài)。利用馬爾可夫鏈的性質(zhì),在不同的領(lǐng)域中,對(duì)不同事件的發(fā)生概率進(jìn)行比較分析,從而可為未來(lái)的良好發(fā)展提供有力的決策依據(jù)。
1.2 隱馬爾可夫模型的基本概念
與理想的馬爾可夫鏈的條件不同,在實(shí)際分析時(shí),存在著一些無(wú)法被觀測(cè)到的確切狀態(tài),將這些無(wú)法觀測(cè)的狀態(tài)看作另一隨機(jī)過(guò)程,因此,隱馬爾可夫模型(HMM)是一個(gè)雙重隨機(jī)過(guò)程。
隱馬爾可夫模型的雙重隨機(jī)過(guò)程可以簡(jiǎn)單地分為馬爾可夫鏈和觀測(cè)過(guò)程[6]。作為第一個(gè)隨機(jī)過(guò)程,馬爾可夫鏈描述不同狀態(tài)之間的轉(zhuǎn)化過(guò)程,該隨機(jī)過(guò)程通常用轉(zhuǎn)移概率矩陣來(lái)描述。而作為隱馬爾可夫模型的第二個(gè)隨機(jī)過(guò)程,觀測(cè)過(guò)程主要是描述狀態(tài)序列與觀測(cè)序列之間的關(guān)系,該隨機(jī)過(guò)程通常用觀察值概率矩陣描述。
在隱馬爾可夫模型中,狀態(tài)除了具有不確定性以外,甚至還會(huì)有隱藏性。只有通過(guò)服從一定規(guī)律的隨機(jī)觀測(cè)狀態(tài),才能將這些不確定的、隱藏的內(nèi)在狀態(tài)體現(xiàn)出來(lái)。因此,從觀測(cè)者的角度而言,只能看到觀測(cè)值,這是因?yàn)殡[馬爾可夫模型中每個(gè)時(shí)刻的觀測(cè)值與狀態(tài)不具備一一對(duì)應(yīng)的映射關(guān)系,而是利用一組概率分布來(lái)聯(lián)系觀測(cè)到的事件與狀態(tài)。基于馬爾可夫鏈,增加另一隨機(jī)過(guò)程來(lái)描述隱藏狀態(tài)的存在及其特性,該模型稱(chēng)之為隱馬爾可夫模型。隱馬爾可夫模型的原理示意如圖1所示。

圖1 隱馬爾可夫模型的原理圖Fig.1 Schematic diagram of the hidden Markov model
圖1中,π為初始概率分布,τ為狀態(tài)空間維數(shù),Τ為觀測(cè)空間維數(shù)。作為馬爾可夫模型的擴(kuò)展,隱馬爾可夫模型主要由5組參數(shù)決定,分別是模型的狀態(tài)數(shù)目N,模型每個(gè)狀態(tài)對(duì)應(yīng)的觀測(cè)特征數(shù)目M,狀態(tài)轉(zhuǎn)移概率分布A,觀測(cè)特征在各個(gè)狀態(tài)的觀測(cè)概率分布B以及初始化狀態(tài)概率分布π。因此,一個(gè)隱馬爾可夫模型可以記作λ=(N,M,π,A,B),簡(jiǎn)寫(xiě)為λ=(π,A,B)[7],典型的隱馬爾可夫模型如圖2所示。

圖2 典型的隱馬爾可夫模型Fig.2 Typical hidden Markov model
對(duì)參數(shù)N,隱馬爾可夫模型的實(shí)際物理狀態(tài)是無(wú)法直接觀測(cè)到的,只能通過(guò)觀測(cè)值序列對(duì) 該物理狀態(tài)進(jìn)行估計(jì)。在隱馬爾可夫模型中,已知觀測(cè)序列中各種可能隱藏狀態(tài)序列可以利用觀測(cè)序列和觀測(cè)值概率進(jìn)行推測(cè)。當(dāng)然,不同觀測(cè)序列的出現(xiàn)概率也可以由觀測(cè)序列和觀測(cè)值概率推測(cè)出來(lái)。隱馬爾可夫模型的隱藏狀態(tài)序列具有隨機(jī)性和馬爾可夫性,隱藏狀態(tài)也可能對(duì)應(yīng)著多個(gè)觀測(cè)值概率。
在隱馬爾可夫模型中,需要統(tǒng)計(jì)每個(gè)狀態(tài)對(duì)應(yīng)的觀測(cè)特征數(shù)目。而觀測(cè)特征添加了物理系統(tǒng)的輸出,在任一時(shí)刻,都可能觀測(cè)到系統(tǒng)的多種特征,這些特征可以用集合的方式表示,即V={v1,v2,…,vM}。在某一段時(shí)間內(nèi),利用上述的觀測(cè)特征,便可以得到一組觀測(cè)序列,記作O={O1,O2,…,OT},其中ot對(duì)應(yīng)著t時(shí)刻的集合V中的某一觀測(cè)值對(duì)象[7]。
狀態(tài)轉(zhuǎn)移概率分布的表達(dá)式如公式(4)所示:

其中,
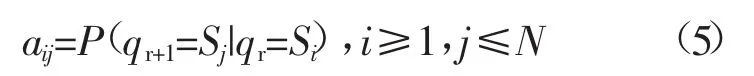
初始概率分布π的表達(dá)式如下:

其中,

1.3 隱馬爾可夫模型解決的問(wèn)題及其相應(yīng)算法
隱馬爾可夫模型主要解決的基本問(wèn)題包括解碼、評(píng)估和學(xué)習(xí)等3個(gè)[8-9]。首先,用一些算法(如Viterbi算法)進(jìn)行解碼。解碼過(guò)程就是根據(jù)已知的模型以及實(shí)驗(yàn)得到的觀測(cè)序列,通過(guò)求解找出這組序列中發(fā)生最大概率的狀態(tài)。然后,利用前向-后向算法進(jìn)行問(wèn)題評(píng)估,即通過(guò)已知模型和觀測(cè)序列求出該序列在模型下出現(xiàn)的概率。最后,利用Baum-Welch算法對(duì)大量的觀測(cè)序列進(jìn)行訓(xùn)練,從而得到一組模型參數(shù)。
隱馬爾可夫模型中三大算法(前向-后向算法、Viterbi算法和Baum-Welch算法)之間的關(guān)系[10]如圖3所示。
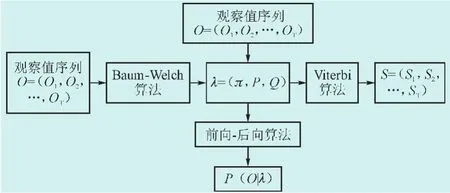
圖3 隱馬爾可夫模型中三大算法關(guān)系圖Fig.3 Analysis of three algorithms in hidden Markov model
1.3.1 前向-后向算法
為解決評(píng)估問(wèn)題,作為一種高效算法,前向-后向算法用來(lái)求解P(O|λ)的值。在解決概率推理問(wèn)題的方法中,這是一種最為常用的方法。直觀來(lái)看,該算法大致分為兩個(gè)部分,即前向、后向。
在前向算法中,首先需要定義前向變量,如:
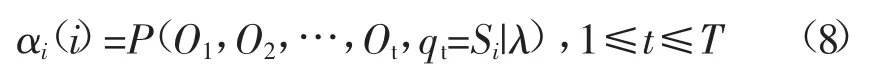
然后,將前向變量進(jìn)行初始化,之后依次是遞歸和終結(jié)。遞歸指的是針對(duì)每個(gè)時(shí)刻和每個(gè)狀態(tài)的順序來(lái)建立兩個(gè)前向變量t時(shí)刻與t+1時(shí)刻之間的關(guān)系,從而得到任一時(shí)刻前向變量值。這種前向算法的優(yōu)點(diǎn)在于復(fù)雜度小,它將N(N+1)(T-1)+N次乘法簡(jiǎn)化為N(N-1)(T-1)次加法,這種算法可以看作是一種典型的格型結(jié)構(gòu)。
后向算法與前向算法相似,也是一種典型的格型結(jié)構(gòu),其主要步驟依次為:定義后向變量,初始化,遞歸,終結(jié)。在后向算法中,其計(jì)算量略大于前向算法,大約在N2T量級(jí)。在實(shí)際應(yīng)用中,后向算法所求出的值通常接近于零,因此,在計(jì)算過(guò)程中常常利用歸一化和對(duì)數(shù)形式求解。
1.3.2 Viterbi算法
Viterbi算法主要是用來(lái)解決當(dāng)觀察值序列和模型給定時(shí),在最佳的意義上確定一個(gè)狀態(tài)序列。例如,已知給定的觀察值序列和模型分別為O=(O1,O2,…,Ot)和λ=(π,A,B),確定狀態(tài)序列Q=(q1,q2,…,qt)。在不同情況下,“最佳”的定義也有所不同,而本文中的“最佳”指的是最大的狀態(tài)序列Q=(q1,q2,…,qt)。
在Viterbi算法中,求解最佳狀態(tài)序列的主要步驟與前向-后向算法相類(lèi)似,求解過(guò)程如下:初始化,遞歸,終結(jié)和求得狀態(tài)序列。初始化過(guò)程中,可以根據(jù)變量定義得到初始化條件。當(dāng)時(shí)間達(dá)到最大時(shí),Viterbi算法終止,與此同時(shí)解得P*的極大值。
從求解過(guò)程不難看出,Viterbi算法也是一種典型的格型結(jié)構(gòu)。它與前向-后向算法的主要區(qū)別在于Viterbi算法是求解以前狀態(tài)的最大值,而前向-后向算法主要是利用求和過(guò)程。因此,實(shí)際應(yīng)用時(shí),通常是利用Viterbi算法求解P*。
1.3.3 Baum-Welch算法
Baum-Welch算法,即期望修正法,廣泛應(yīng)用于解決學(xué)習(xí)問(wèn)題。Baum-Welch算法的基本原理是利用迭代更新來(lái)得到模型參數(shù)的局部最優(yōu)解[8]。首先對(duì)隱馬爾可夫模型中的各參數(shù)π、A、B,即λ=(π,A,B),進(jìn)行參數(shù)重估,得到新的參數(shù)模型,然后對(duì)隱馬爾可夫模型進(jìn)行迭代更新,最后得到模型參數(shù)的局部最優(yōu)解。
Baum-Welch算法的求解過(guò)程也與前兩種算法類(lèi)似,主要步驟依次為:初始化,更新模型參數(shù)、終止。所謂的初始化就是根據(jù)變量的定義給定模型參數(shù)λ=(π,A,B),得到初始條件。在進(jìn)行參數(shù)重估之前,還需要定義兩個(gè)參數(shù)ζt(i,j)和γt(i)。其中ζt(i,j)表示t時(shí)刻為Si,t+1時(shí)刻為Sj的概率;γt(i)表示,在已知觀測(cè)序列的條件下,t時(shí)刻的狀態(tài)為Si的概率。利用公式對(duì)上述兩個(gè)參數(shù)ζt(i,j)和γt(i)進(jìn)行計(jì)算,并將隱馬爾可夫模型中的參數(shù)進(jìn)行重新估計(jì),從而得到新的隱馬爾可夫模型參數(shù)λ′=(π′,A′,B′)。重復(fù)迭代計(jì)算Q(λ,λ′),直到滿足迭代次數(shù)或連續(xù)兩次概率的增量比設(shè)定值小。
1.4 隱馬爾可夫模型的分類(lèi)
隱馬爾可夫模型的許多特性都可以用來(lái)解決現(xiàn)實(shí)生活中的許多實(shí)際問(wèn)題,其分類(lèi)可以有多種。從處理的數(shù)據(jù)類(lèi)型角度來(lái)看,隱馬爾可夫模型可以分為離散型和連續(xù)型。在現(xiàn)實(shí)生活中,許多實(shí)際的物理量都是連續(xù)的,也可認(rèn)為這需要處理的數(shù)據(jù)也是連續(xù)的,例如語(yǔ)音信號(hào)識(shí)別,股票幾個(gè)時(shí)間序列預(yù)測(cè),人臉識(shí)別和人體運(yùn)動(dòng)識(shí)別等。當(dāng)然,在現(xiàn)實(shí)世界中,也有少數(shù)數(shù)據(jù)是離散的,因此觀測(cè)值屬于離散量,故稱(chēng)為離散型馬爾可夫模型。
根據(jù)馬爾可夫模型實(shí)現(xiàn)方式,又可分為遍歷型馬爾可夫模型、自回歸馬爾可夫模型、輸入輸出馬爾可夫模型、因子馬爾可夫模型和耦合馬爾可夫模型[10]。其中,耦合隱馬爾可夫模型是指將傳統(tǒng)隱馬爾可夫模型中的單條馬爾可夫鏈擴(kuò)展為多條馬爾可夫鏈。耦合隱馬爾可夫模型中,雖然各馬爾可夫鏈在時(shí)間上可能發(fā)生交叉的情況,但是每條馬爾可夫鏈自身是相對(duì)獨(dú)立的,生成的觀察序列也是互不影響的。實(shí)際上,可以將耦合隱馬爾可夫模型看作在多個(gè)隱馬爾可夫序列之間引入耦合條件概率從而得到多馬爾可夫模型[10]。
2 隱馬爾可夫模型在電力系統(tǒng)連鎖故障預(yù)測(cè)中的應(yīng)用
在電力系統(tǒng)中,如果某一級(jí)線路發(fā)生故障,將會(huì)引起下一級(jí)的故障。如果能夠及時(shí)的將單一的故障清除,將不會(huì)導(dǎo)致整個(gè)系統(tǒng)的崩潰。然而,在某段時(shí)間內(nèi),如果大量元件因?yàn)楫a(chǎn)生過(guò)載保護(hù)動(dòng)作而停止工作,那么,電力系統(tǒng)將會(huì)快速的進(jìn)入崩潰狀態(tài)。因此,將會(huì)出現(xiàn)大面積的停電,給經(jīng)濟(jì)帶來(lái)巨大的損失。利用隱馬爾可夫模型,對(duì)電力系統(tǒng)中的安全隱患進(jìn)行預(yù)測(cè),大大降低了電力系統(tǒng)事故甚至大面積停電等發(fā)生的概率。此外,實(shí)驗(yàn)證明,利用隱馬爾可夫模型對(duì)電力系統(tǒng)進(jìn)行連鎖故障預(yù)測(cè),其準(zhǔn)確率通常在97.5%左右[11]。
2.1 基于馬爾可夫模型連鎖故障預(yù)測(cè)的流程
在利用馬爾可夫模型進(jìn)行電力系統(tǒng)連鎖故障預(yù)測(cè)的過(guò)程中,首先需要選擇一條故障路線并判斷該故障路線的故障原因,該故障原因可定義為故障i。然后任一選取一條路徑n作為研究對(duì)象,計(jì)算線路n發(fā)生初始故障的概率P。通過(guò)一系列的條件判斷后,計(jì)算線路n的綜合狀態(tài)轉(zhuǎn)移概率。然后,將該計(jì)算結(jié)果代入馬爾可夫鏈的預(yù)測(cè)模型中,從而計(jì)算線路的故障概率。通過(guò)計(jì)算比較,選出故障概率值最大的線路作為當(dāng)前線路的下一級(jí)故障線路,并對(duì)整個(gè)電力系統(tǒng)進(jìn)行脆弱性分析。重復(fù)上述的預(yù)測(cè)過(guò)程,對(duì)電路系統(tǒng)的故障預(yù)測(cè)進(jìn)行逐級(jí)分析。
通過(guò)比較逐級(jí)掃描前一級(jí)線路切除后其他線路發(fā)生故障的概率值,選出最大概率值所對(duì)應(yīng)的線路,利用這種方式,對(duì)每條路徑的發(fā)生故障的概率進(jìn)行綜合評(píng)價(jià),針對(duì)不同故障概率值,提前采取相關(guān)的應(yīng)對(duì)措施,從而減少電力系統(tǒng)連鎖故障的發(fā)生。
2.2 實(shí)例分析
在電力系統(tǒng)中,因潮流轉(zhuǎn)移而引發(fā)的線路過(guò)載是發(fā)生連鎖故障的主要原因。此外,由于保護(hù)或斷路器的錯(cuò)誤動(dòng)作以及系統(tǒng)硬件失效等其他小概率事件,系統(tǒng)狀態(tài)也會(huì)加速惡化,最終導(dǎo)致電力系統(tǒng)崩潰,發(fā)生大面積停電事故。
為更好地預(yù)測(cè)電力系統(tǒng)故障,需要對(duì)由潮流轉(zhuǎn)移導(dǎo)致的狀態(tài)轉(zhuǎn)移概率進(jìn)行分析和計(jì)算。系統(tǒng)的運(yùn)行狀態(tài)不同,潮流轉(zhuǎn)移引起的狀態(tài)轉(zhuǎn)移概率也會(huì)有所不同。
以IEEE 10機(jī)39節(jié)點(diǎn)的系統(tǒng)為例,利用隱馬爾可夫模型對(duì)電力系統(tǒng)故障進(jìn)行預(yù)測(cè),IEEE 10機(jī)39節(jié)點(diǎn)系統(tǒng)如圖4所示。
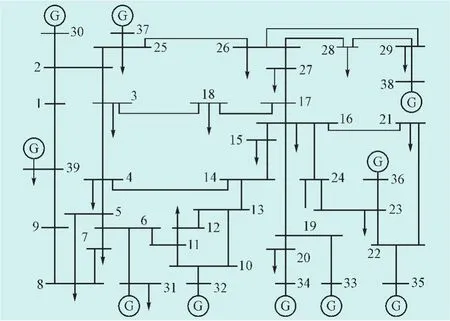
圖4 IEEE 10機(jī)39節(jié)點(diǎn)系統(tǒng)Fig.4 IEEE 10 machine 39 node system
如果該系統(tǒng)發(fā)生m級(jí)電路故障,根據(jù)馬爾可夫模型連鎖故障預(yù)測(cè)的流程,不難算出故障線路以外的綜合狀態(tài)轉(zhuǎn)移概率。如果上一級(jí)在同一線上發(fā)生故障,該線路成為下一級(jí)連鎖故障的可能性將會(huì)受轉(zhuǎn)移概率的影響。一般來(lái)講,轉(zhuǎn)移概率的值越大,該線路越容易成為下一級(jí)的故障線路。因此,通過(guò)對(duì)發(fā)生故障以外的線路的綜合狀態(tài)轉(zhuǎn)移概率進(jìn)行比較,選出概率值最大的那一條作為次級(jí)連鎖故障。
為計(jì)算圖4中發(fā)生故障時(shí)綜合狀態(tài)轉(zhuǎn)移概率(Pm_k),我們做出如下假設(shè):
1)故障級(jí)數(shù)m=8;
2)將m=2級(jí)故障作為前一級(jí)故障可能性最大的兩條路線;
3)出于某些原因,線路13-14發(fā)生故障。
當(dāng)m=8時(shí),線路4-14和線路3-4的綜合狀態(tài)轉(zhuǎn)移概率分別為0.702 5和0.862 4;當(dāng)m=7時(shí),線路15-16和線路29-38的綜合狀態(tài)轉(zhuǎn)移概率分別為0.843 4和0.983 1;當(dāng)m=6時(shí),線路22-23和線路16-19的綜合狀態(tài)轉(zhuǎn)移概率分別為0.683和0.905 8。
由此可見(jiàn),不同的故障路徑所對(duì)應(yīng)的系統(tǒng)脆弱性指標(biāo)值有所不同。電力系統(tǒng)脆弱性指標(biāo)是對(duì)系統(tǒng)承受干擾或故障的能力的描述,主要包括:負(fù)荷損失指標(biāo)、輸電能力下降指標(biāo)、最大聯(lián)通與比率指標(biāo)。以系統(tǒng)脆弱性指標(biāo)作為輔助依據(jù),有利于運(yùn)行人員對(duì)可能發(fā)生的連鎖故障進(jìn)行整體上的掌控。當(dāng)然,在實(shí)際應(yīng)用中,發(fā)生故障的線路不一定是故障概率值最大的路徑。因此,在對(duì)實(shí)際電力系統(tǒng)進(jìn)行連鎖故障預(yù)測(cè)時(shí),還需考慮其他故障概率較大路徑的影響。
3 結(jié)論
電力系統(tǒng)的連鎖故障將會(huì)導(dǎo)致大面積停電事故,給人們的生活帶來(lái)很多不便。為了能夠清晰地將故障觀測(cè)狀態(tài)與隱藏狀態(tài)的對(duì)應(yīng)關(guān)系描述出來(lái),通過(guò)建立隱馬爾可夫模型,能夠有效地預(yù)測(cè)下一級(jí)故障的發(fā)生概率。本文對(duì)隱馬爾可夫模型的基本理論和模型構(gòu)建進(jìn)行了總結(jié)和分析,通過(guò)工程實(shí)例,進(jìn)一步分析了基于隱馬爾可夫模型進(jìn)行電力系統(tǒng)連鎖故障預(yù)測(cè)需要考慮的因素,并得出如下結(jié)論:
1)在電力系統(tǒng)中,連鎖故障之間的每一級(jí)都是相互影響的,每級(jí)之間都存在著某種對(duì)應(yīng)關(guān)系。因此,為了能準(zhǔn)確地預(yù)測(cè)出次級(jí)發(fā)生故障的概率,需要充分地考慮前后級(jí)故障之間的狀態(tài)轉(zhuǎn)移關(guān)系。
2)利用隱馬爾可夫模型對(duì)電力系統(tǒng)進(jìn)行連鎖故障預(yù)測(cè),能夠準(zhǔn)確地計(jì)算出狀態(tài)轉(zhuǎn)移概率和斷路器異常動(dòng)作概率,從而逐級(jí)預(yù)測(cè)故障的發(fā)生。
3)對(duì)于電力系統(tǒng)中各模塊的退化狀態(tài),隱馬爾可夫模型可以準(zhǔn)確的識(shí)別出來(lái),有效地預(yù)測(cè)連鎖故障發(fā)生概率。例如在實(shí)例分析中,當(dāng)線路13-14發(fā)生故障退出運(yùn)行后,通過(guò)對(duì)各級(jí)的綜合狀態(tài)轉(zhuǎn)移概率來(lái)預(yù)測(cè)下級(jí)發(fā)生故障的可能性,從而有效地控制連鎖故障的發(fā)生。
[1]程林,劉滿君,易俊,等.基于運(yùn)行可靠性模型的連鎖故障模擬及薄弱環(huán)節(jié)分析 [J].電網(wǎng)技術(shù).2016,40(5):1488-1494.CHENG Lin,LIU Manjun,YI Jun,et al.Fuzzy-chain simulation and weak link analysis based on operational reliability model[J].Power System Technology,2016,40(5):1488-1494.
[2]吳文可.電力系統(tǒng)故障診斷模型與事故處理輔助決策方法[D].廣州:華南理工大學(xué),2013.
[3]程林,劉滿君,何劍,等.基于馬爾可夫過(guò)程的電力系統(tǒng)連鎖故障解析模型及概率計(jì)算方法[J].電網(wǎng)技術(shù),2017,41(1):130-136.CHENG Lin,LIU Manjun,HE Jian,et al.An analytical model and probability calculation method for cascading failures in power system[J].Power System Technology,2017,41(1):130-136.
[4]吳文可,文福拴,薛禹勝,等.基于馬爾可夫鏈的電力系統(tǒng)連鎖故障預(yù)測(cè) [J].電力系統(tǒng)自動(dòng)化,2013,37(5):29-37.WU Wenke,WEN Fushuan,XUE Yusheng,et al.A Markov chain based model for forecasting power system cascading failures[J].Automation of Electric Power Systems 2013,37(5):29-37.
[5]張樺.配電系統(tǒng)可靠性預(yù)測(cè)模型及其算法研究 [D].重慶:重慶大學(xué),2016.
[6]夏麗莎.基于隱馬爾可夫模型的故障診斷及相關(guān)算法研究[D].武漢:華中科技大學(xué),2014.
[7]田沿平,葉曉慧,金川,等.耦合隱馬爾可夫在模擬電路故障預(yù)測(cè)中的應(yīng)用[J].電子測(cè)量技術(shù),2014,37(10):135-138.TIAN Yanping,YE Xiaohui,JIN Chuan,et al.Application of coupled hidden Markov model in analog circuit fault prediction[J].Electronic Measurement Technology,2014,37(10):135-138.
[8]劉韜.基于隱馬爾可夫模型與信息融合的設(shè)備故障診斷與性能退化評(píng)估研究[D].上海:上海交通大學(xué),2014.
[9]胡為,高雷,傅莉.基于最優(yōu)階次HMM的電機(jī)故障診斷方法研究[J].儀器儀表學(xué)報(bào),2013,34(3):524-530.HU Wei, GAO Lei, FU Li.Research on motor fault detection method based on optimal order hidden Markov model[J].Chinese Journal of Scientific Instrument,2013,34(3):524-530.
[10]龍百元.基于層次分析法和隱馬爾可夫模型的風(fēng)險(xiǎn)評(píng)估方法研究[D].長(zhǎng)沙:湖南大學(xué),2007.
[11]柳楠.基于隱馬爾可夫模型的航空機(jī)械系統(tǒng)故障診斷算法設(shè)計(jì)[J].現(xiàn)代工業(yè)經(jīng)濟(jì)和信息化,2016,6(5):44-45.LIU Nan.The design of aviation mechanical system fault diagnosis algorithm based on hidden Markov model[J].Modern Industrial Economy and Information Technology,2016,6(5):44-45.
Power System Cascading Failure Prediction Based on Hidden Markov Model
DING Yan1,GUO Heqiang2,WANG Lili1,LI Qiuyan1,SUN Yihao1,GUAN Chaojie1
(1.State Grid Henan Economic Research Institute,Zhengzhou 450001,Henan,China;2.Tianjin Tianda Qiushi Electric Power High Technology Co.,Ltd.,Tianjin 300001,China)
In recent years,the power system is gradually developing toward a complex,integrated and intelligent system.Cascading failures of power systems will result in blackouts in large areas and brings a lot of inconvenience to people′s lives.Therefore,prediction of cascading failures is getting more and more important in the field of power systems.However,because of complexity of the network,correlation between faults and uncertainty of the power system,the existing fault prediction methods are not applicable any more.To this end,this paper presents a cascading failure prediction method based on Markoff model.Using the hidden Markov model to predict the fault of the power system,it is possible to accurately calculate the state transition probability or the abnormal probability of the circuit breaker,so as to predict occurrence of the fault step by step.The hidden Markov model can identify the degradation state of each module in power systems,and effectively predict the probability of cascading failures.
power system;cascading failure;hidden Markov;faultprediction
近年來(lái)電力系統(tǒng)逐漸向復(fù)雜化、集成化和智能化的方向發(fā)展。電力系統(tǒng)的連鎖故障將會(huì)導(dǎo)致大面積停電事故,給人們的生活帶來(lái)很多不便。因此,在電力系統(tǒng)領(lǐng)域,對(duì)連鎖故障的預(yù)測(cè)地位日益凸顯。然而,網(wǎng)絡(luò)的復(fù)雜性、故障間的關(guān)聯(lián)性和系統(tǒng)的不確定性使得現(xiàn)有的故障預(yù)測(cè)方法并不適用。因此,提出基于隱馬爾可夫模型對(duì)電力系統(tǒng)連鎖故障進(jìn)行預(yù)測(cè)。該模型能夠準(zhǔn)確地計(jì)算出狀態(tài)轉(zhuǎn)移概率或斷路器異常動(dòng)作概率,從而逐級(jí)預(yù)測(cè)故障的發(fā)生。對(duì)于電力系統(tǒng)中各模塊的退化狀態(tài),隱馬爾可夫模型可以準(zhǔn)確地識(shí)別出來(lái),有效地預(yù)測(cè)連鎖故障發(fā)生概率。
電力系統(tǒng);連鎖故障;隱馬爾可夫;故障預(yù)測(cè)
1674-3814(2017)09-0093-06
TM76
A
國(guó)家自然科學(xué)基金資助項(xiàng)目(51190103);國(guó)家電網(wǎng)公司科技資助項(xiàng)目(5217L0150005)。
Project Supported by the National Natural Science Foundation of China(51190103);the Science and Technology Program of State Grid Corporation of China(5217L0150005).
2016-10-25。
丁 巖(1988—),男,工程師,本科學(xué)歷,研究方向:電力系統(tǒng)規(guī)劃設(shè)計(jì)。
(編輯 李沈)

