如何研究雙變量的最值問(wèn)題

楊 帆

(江蘇省海門(mén)中學(xué) 226100)

如何研究雙變量的最值問(wèn)題

楊 帆

(江蘇省海門(mén)中學(xué) 226100)

本文就雙變量的最值問(wèn)題，分類(lèi)舉例加以說(shuō)明，由此歸納出一般的解題原則.

雙變量；最值問(wèn)題；范圍

近幾年的高考或者大市級(jí)的高考模擬卷中都考到雙變量的最值或者取值范圍問(wèn)題，而這類(lèi)問(wèn)題學(xué)生在處理的時(shí)候往往比較棘手，短時(shí)間內(nèi)找不到合適的方法，在考試的時(shí)候浪費(fèi)了很多的時(shí)間，走了很多彎路.本文主要針對(duì)這類(lèi)問(wèn)題利用三個(gè)主要例題及其相應(yīng)的變式題目，進(jìn)行一下探索和方法的總結(jié).有這些方法的思考和意識(shí)，希望能為學(xué)生思路的打開(kāi)起到作用.

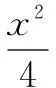
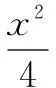
所以令f(t)=-12t2-2t+12,t∈[-1,1]，

評(píng)析這道題求目標(biāo)函數(shù)3x2-2y的最值，看似其里面有兩個(gè)變量的，其實(shí)有條件的方程約束，本質(zhì)上為單變量的最值問(wèn)題，因此首先想到消元，采用代入消元法.

變題1 條件不變，問(wèn)題改為：求3x-2y的最值.

變題2 條件不變，問(wèn)題改為：求3x2-2xy的最值.

解析在這道題中，目標(biāo)函數(shù)的幾何意義顯然不容易發(fā)現(xiàn)，所以采用三角消元比較合適，但是三角消元也是具有一定的局限性，對(duì)條件中關(guān)于雙變量的方程的結(jié)構(gòu)要求較特殊.

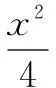
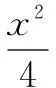
評(píng)析這道題目的特點(diǎn)是：目標(biāo)函數(shù)代入消元不好處理，目標(biāo)函數(shù)沒(méi)有明顯的幾何意義，條件的形式不好用三角替換.在這種情況下，雖然條件是關(guān)于雙變量的方程，本質(zhì)上問(wèn)題中含有一個(gè)變量，但是難點(diǎn)就在于如何將二元化為一元，這時(shí)我們常用的技巧就是：能不能將條件中的方程用參數(shù)方程表示(觀察是否能因式分解)達(dá)到消元目的；觀察目標(biāo)函數(shù)的結(jié)構(gòu)是否具有某種特點(diǎn)，進(jìn)行相關(guān)配湊，整體換元到達(dá)消元目的；將目標(biāo)函數(shù)令為t，反過(guò)來(lái)表示代入條件方程，轉(zhuǎn)化為方程有解問(wèn)題(本質(zhì)上換主元)，將t視作參數(shù)，達(dá)到研究t的取值范圍的目的.

通過(guò)以上幾個(gè)題目我們發(fā)現(xiàn)實(shí)際上這類(lèi)在方程約束下的雙變量最值問(wèn)題，本質(zhì)上難點(diǎn)就在于如何將二元化為一元，我們?cè)诮鉀Q問(wèn)題時(shí)應(yīng)該想到以下幾種方法：①代入消元；②三角消元；③目標(biāo)函數(shù)的幾何意義；④條件方程轉(zhuǎn)化為參數(shù)方程；⑤整體換元；⑥令目標(biāo)函數(shù)為t回代條件方程轉(zhuǎn)化為方程有解問(wèn)題.當(dāng)然以上幾種方法解題時(shí)都要注意變量的范圍.

剛剛這類(lèi)問(wèn)題是方程約束下的雙變量最值問(wèn)題，其實(shí)還有一類(lèi)題目雖然雙變量在條件中有方程的約束，但不是求某個(gè)目標(biāo)函數(shù)的取值范圍，而是個(gè)固定的值.這類(lèi)雙變量問(wèn)題中，不能用以上幾個(gè)方法，我們?cè)撊绾嗡伎迹旅嫖襾?lái)看一道題.

法二：在法一中得到了：s+t-2=ln(st)即s+t-2=lns+lnt,整理一下得到：s-lns+t-lnt=2.由法一中研究的f(x)=lnx-x+1得：s-lns≥1,t-lnt≥1，所以要使得s-lns+t-lnt=2，只能s=1,t=1，所以xy=1.

總之，我們?cè)谘芯侩p變量問(wèn)題的過(guò)程，應(yīng)該站在由多元化一元，由雜亂化統(tǒng)一的角度去思考，去嘗試.

[1] 陳慶洪.淺析高考數(shù)學(xué)中的最值問(wèn)題[J]. 福建中學(xué)數(shù)學(xué),2012(01).

[2] 司麥領(lǐng).函數(shù)應(yīng)用題中的最值問(wèn)題選解[J]. 中學(xué)生數(shù)理化(高中版·學(xué)研版),2011(05).

[3] 康小峰.高考應(yīng)用性題型解析及求解策略[J]. 中學(xué)數(shù)學(xué)雜志,2011(01).

G632

A

1008-0333(2017)31-0020-03

2017-07-01

楊帆(1985.03-)，男，江蘇省南通人，本科，中級(jí)職稱(chēng)，從事高中數(shù)學(xué)教學(xué)與研究.

楊惠民]