基于對比度增強抑制灰度的改進優化準則法

許小奎 郭寶峰 金 淼

燕山大學先進鍛壓成形技術與科學教育部重點實驗室，秦皇島，066004

基于對比度增強抑制灰度的改進優化準則法

許小奎 郭寶峰 金 淼

燕山大學先進鍛壓成形技術與科學教育部重點實驗室，秦皇島，066004

為了抑制變密度法拓撲優化結果中的灰度單元，基于對比度增強策略，提出了兩種形式的對比度增強算子，引入到優化準則法迭代計算中，對優化準則法進行了改進。對比度增強算子能夠拉大單元灰度差別，驅動中間密度向兩極進行分化，最終使優化收斂于0/1材料分布狀態。采用典型數值算例對該方法進行了驗證，計算結果表明，該方法能夠得到拓撲結構清晰的優化結果。

拓撲優化；對比度增強；灰度單元；優化準則法

0 引言

在機械結構設計中，結構拓撲優化為初期結構的選型提供了一種高效的技術手段，能夠幫助設計者設計出創新型可靠產品。結構拓撲優化主要研究結構所用材料的最優分布問題，是當前結構優化設計領域中最具挑戰性和經濟效益的研究方向之一。

在連續體結構的拓撲優化研究中，變密度法[1]自被提出以來，因其求解效率高、易于實施等特點，得到了廣泛的應用。基于有限元技術的變密度法在求解結構拓撲優化問題時，會不可避免地出現棋盤格問題[2]，為此，應用變密度法的拓撲優化求解中大多采取了基于圖像處理的過濾技術[3-4]。過濾技術解決了棋盤格問題，但卻在結構的邊緣區域又形成了灰度單元，使得結構邊緣擴散而不清晰，影響了結果的后續提取與加工，為直接工程化應用帶來了困難。

為了解決灰度單元問題，研究人員提出了許多方法。早期一般采用簡單后處理方法，如閾值控制法等，其結果一般不再滿足約束條件。密度過濾結合Heaviside函數的方法包括Heaviside過濾[5]、改進Heaviside過濾[6]和體積保持的Heaviside過濾方法[7]，可以得到清晰的優化結果，但其優化需要較多的迭代步數，優化效率較低。基于形態學的方法[6]同樣需要較多的迭代步數。BORRVALL等[8]采用增加約束的方法但會使優化求解過程變得復雜。GROENWOLD等[9]對優化準則進行了修改，將單元密度向單極進行壓縮，實現了灰度單元的抑制。張志飛等[10]采用過濾與不過濾交替實施的優化方法，但存在棋盤格再次出現的可能。陳垂福等[11]提出了一種變過濾半徑的敏度過濾方法，但失去了過濾半徑控制最小尺寸的特點。還有一些其他的方法，如非線性擴散技術[12]、雙邊濾波方法[13]等，對過濾方法進行了修改，但都需要經驗來確定合適的調節參數，從而優化得到理想的結果。

本文采用圖像處理中的對比度增強技術，實現對灰度單元的抑制。對比度增強技術主要是通過擴大圖像灰度差別、增強灰度對比的方法，使圖像特征得到加強。本文構造了兩種形式的對比度增強算子，將其引入到優化準則法(optimality criteria,OC)迭代計算中，使單元密度向兩極分化，以得到邊緣清晰的優化結果。該方法不需要添加附加約束條件，僅對優化準則進行了修改，實施過程簡便。同時，借助OC法求解，使得優化具有較高的求解效率。

1 連續體結構拓撲優化

1.1 優化模型

基于變密度法建立優化模型，體積約束條件下求結構最小柔度的優化問題可以表示為

(1)

式中，ρ為相對密度(即設計變量)；C為結構柔度；K和U分別為結構總剛度矩陣和總位移矩陣；ke和ue分別為單元剛度矩陣和單元位移矩陣；ρe為單元相對密度；Ve為單元體積；V*為目標體積；n為結構中單元總數。

變密度法中對中間密度的材料屬性進行了描述，本文采用改進的SIMP(solid isotropic microstructures with penalization)對材料屬性進行描述，單元的彈性模量表示為

(2)

式中，E0為實體單元的彈性模量；Emin為空洞單元的彈性模量，為了防止剛度矩陣奇異，通常設置為大于0的值；p為懲罰系數。

柔度和體積的敏度分別為

(3)

(4)

式中，ke0為單位彈性模量的單元剛度矩陣。

1.2 基于OC法的問題求解

通過OC法進行優化求解時，迭代公式可以表達為

(5)

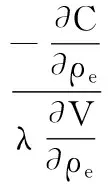
(6)

式中，m和η分別為移動極限和阻尼系數，是保證迭代穩定和收斂的控制參數，本文中取m=0.2，η=0.5；λ為拉格朗日乘子，在每次迭代中根據體積約束條件采用二分法對其進行求解。

直接采用式(5)進行迭代求解，會出現棋盤格問題，需要進行過濾處理。

1.3 過濾處理

過濾處理方法如圖1所示，對于任意單元e，以其中心為圓心，以半徑rmin作圓，圓形區域Ωe是單元e的過濾影響范圍。敏度的過濾處理表達式為

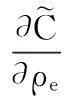
(7)

Hi=rmin-d(i,e)

(8)

i=1,2,…，Ne

其中，Ne為過濾范圍內單元的數量；Hi為距離權重；d(i,e)為過濾范圍內單元i和中心單元e的距離。為防止ρe為0時用作分母，ρe取為max(ρe,10-3)。

圖1 網格過濾示意圖Fig.1 The filtering scheme

將過濾之后的柔度敏度(式(7))替代迭代公式(式(5))中的柔度敏度，可以有效消除棋盤格問題，但由于過濾方法均化作用的影響，又使得結構的邊緣區域出現大量灰度單元，邊緣擴散而不清晰。圖2所示是應用過濾處理的優化結果，結構邊緣模糊且呈現為斜坡型邊緣，其剖切平面如圖3a所示，而理想的結構邊緣應是階躍型邊緣(圖3b)。結構邊緣的剖切平面是沿結構邊緣的法向進行剖切所得到的平面。過濾半徑rmin越大，優化結果中的灰度單元就會越多，斜坡越緩。

圖2 過濾優化結果Fig.2 The result with filtering treatment

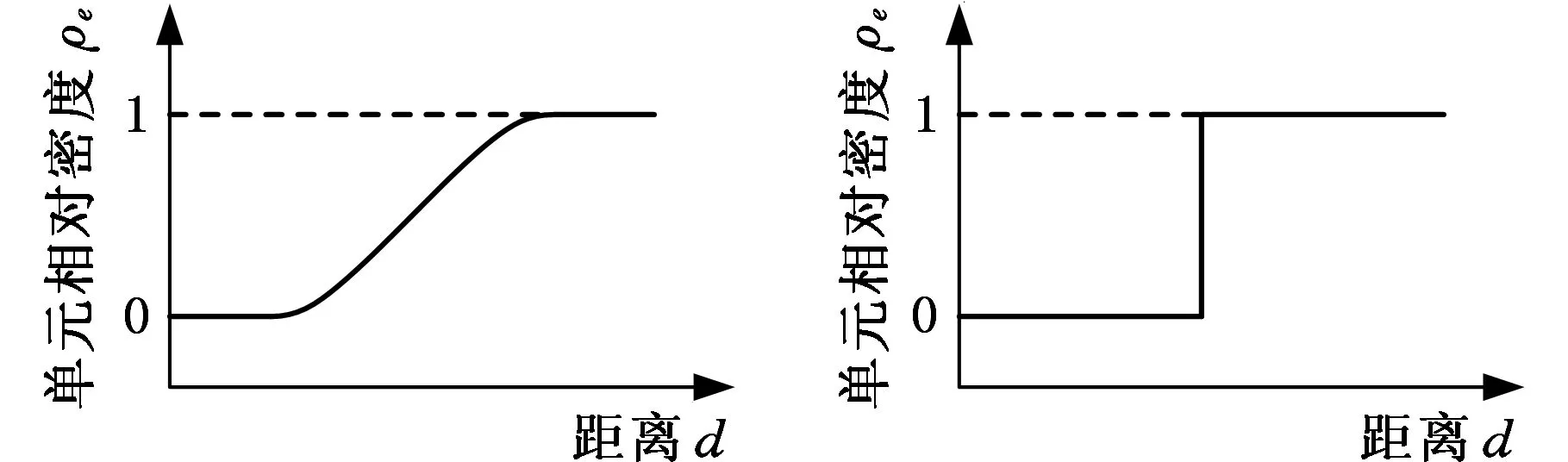
(a)斜坡型邊緣 (b)階躍型邊緣圖3 結構邊緣剖切平面圖Fig.3 The sectional drawing of structure edge

2 基于對比度增強的改進優化準則法

對比度增強是一種通過改變灰度值來改變圖元的對比度，從而改善圖像質量的圖像處理方法。通常根據需求將原有的灰度值通過函數變換進行重新映射，達到增強圖像特征的目的。

下面借助對比度增強方法，實現抑制拓撲優化結果中的灰度單元、增強結構的邊緣特征的目的，進而得到理想階躍型的結構邊緣。在實施過程中，構造了對比度增強算子，在過濾處理之后，將其引入到準則迭代計算中，對準則迭代中的相對密度進行修改，表達式為

(9)

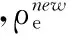
由于優化準則法采用二分法求解拉格朗日乘子以使結果滿足體積約束，故應用修改之后的迭代公式進行優化求解能夠保證體積約束條件得到滿足。

對比度增強算子應起到抑制中間密度，使單元密度兩極分化，增強邊緣的作用。為此，本文提出了兩種分段線性變換的對比度增強算子，如圖4所示。分段線性變換的優點是可以拉伸感興趣的灰度區間，抑制不感興趣的灰度級，使得細節特征得到突出。

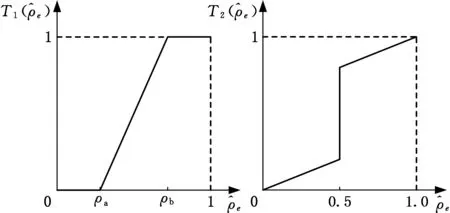
(a)算子1 (b)算子2圖4 對比度增強算子Fig.4 The contrast enhancement operator

算子1的表達式為

(10)

式中，c1為斜率控制參數，c1≥1。

如圖4a所示，算子1將低密度邊緣[0,ρa]調整為0、將高密度邊緣[ρb, 1]調整為1、將中間密度范圍(ρa,ρb)線性拉伸到(0,1)，即算子1通過截取一定范圍內的中間密度并拉伸至整個密度范圍，以提高單元密度對比度，達到增強邊緣的目的。隨著c1的增大，對比度增大越明顯，當c1→∞時，算子1退化為閾值函數。

算子2的表達式為

(11)

式中，c2為斜率控制參數，0≤c2≤1。

如圖4b所示，算子2將[0,0.5)內的密度向下進行壓縮，將[0.5,1]內的密度向上進行壓縮，增大了兩個區間密度之間的差異，因而能夠達到增強邊緣的目的。隨著c2的減小，對比度增大越明顯，當c2→0時，算子2退化為閾值函數。

在拓撲優化計算過程中，對比度增強算子的參數大小應當選擇合適，以保證迭代過程穩定快速收斂。迭代計算的初期，是主體框架的成形期，大的對比度增強算子會引起對單元密度改變過多從而導致刪除單元過多，進而影響隨后的最優結果的搜索，因此，應該采用較小的對比度增強效果或不采用增強效果。在迭代計算的后期，拓撲結果演變緩慢且變化幅度較小，此時應采用較大的對比度增強效果，使迭代快速收斂。

根據上述思路，設計對比度增強算子的參數取值。對于大多數結構的優化計算，當設計變量的最大變化量小于0.07時，形成了拓撲結構的主體框架，此時的迭代步數記為k(c<0.07)。在拓撲結構的主體框架形成過程中，不對單元密度進行對比度增強處理。當主體框架形成之后，采用逐步增強的對比度增強算子進行優化求解。

在實施過程中，設定c1的變化表達式為

(12)

c2的變化表達式為

(13)

式中，k為迭代次數；Δ1和Δ2為變化幅度。

c1和c2的變化曲線如圖5所示。在迭代步數達到k(c<0.07)以前，c1和c2都保持不變；在迭代步數k(c<0.07)以后，c1逐漸增大，c2逐漸減小，Δ1和Δ2分別控制c1和c2變化的幅度。在本文優化算例中取Δ1=0.03，Δ2=0.02。

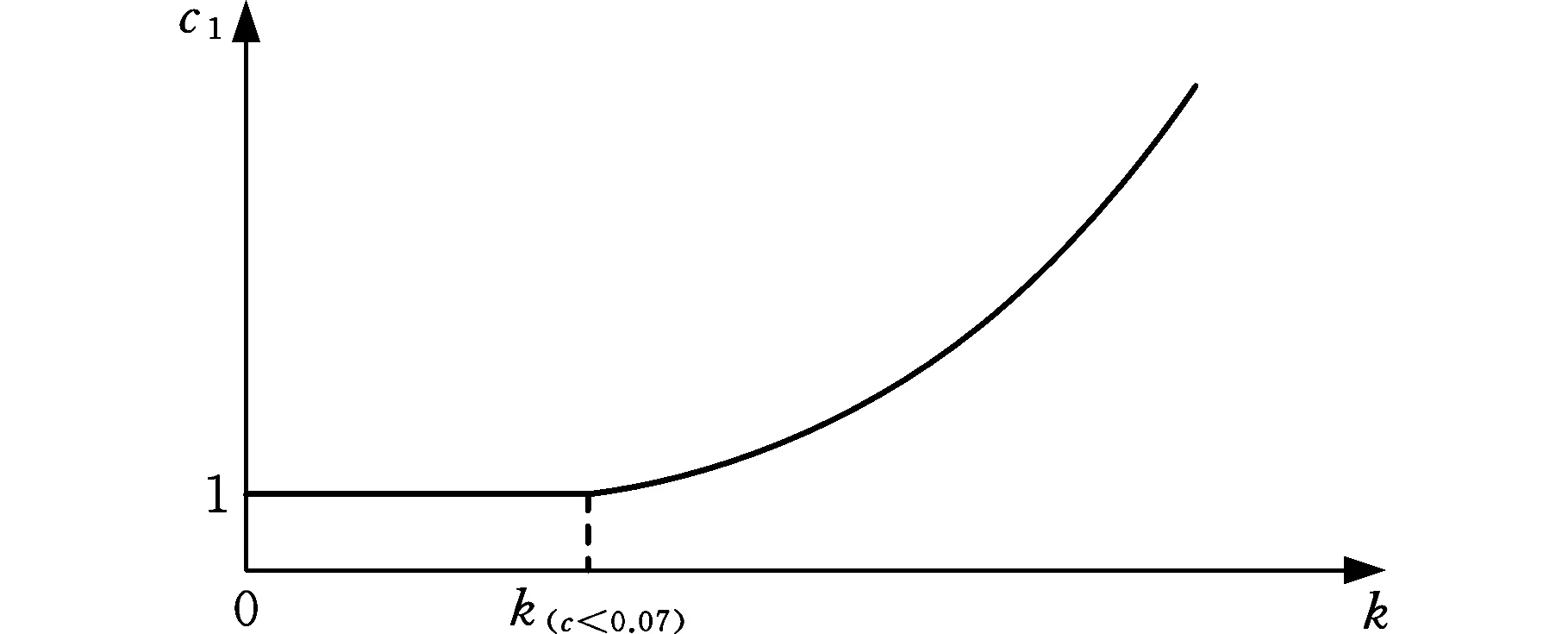
(a)c1

(b)c2圖5 c1和c2的變化曲線Fig.5 The varying curves of c1 and c2

為了保證迭代過程的穩定，還應該保持每次迭代中單元密度的變化在移動極限內。

本文采用的兩種對比度增強算子驅動中間密度向兩極進行分化，與文獻[5]中的向單極進行壓縮相比，更有利于優化得到最優拓撲結構。

3 算例與分析

采用下面典型的連續體結構拓撲優化數值算例對本文方法進行驗證。算例中的結構均采用四邊形單元進行離散，設材料的彈性模量E0=1，Emin=10-9，泊松比為0.3，懲罰因子p為3。優化迭代終止的判定條件為max|ρ(k+1)-ρ(k)|≤0.01。

為了衡量優化結果中灰度單元的比例，采用灰度單元占比δ進行描述，表達式為

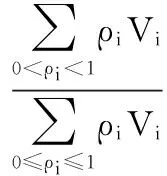
(14)

δ的值越大，表示存在的灰度單元越多。當結果中的所有單元都是灰度單元時，δ為1；當結果中的單元密度非0即1時，δ為0。

算例1 圖6所示為一個懸臂梁，設計域大小為100 mm×50 mm，厚度為1 mm。左側固定，右側中間作用豎直向下的載荷F，大小為1 N。設計域離散為100×50個單元，設計域體積的50%作為目標體積，過濾半徑取為3.5 mm。算例1的優化結果構型如圖7所示，圖7a為應用OC方法優化的結果，圖7b、圖7c分別為引入對比度增強算子1、2的優化結果，圖7d為采用文獻[5]中方法的優化結果。圖8所示為優化結構邊緣的剖切平面密度變化圖，剖切線的位置如圖7a和圖7b中黑線所示。各優化結果的柔度、灰度占比和迭代次數如表1所示。

圖6 算例1設計域及邊界條件Fig.6 Design domain and boundary conditions of example 1

(a)OC方法 (b)算子1

(c)算子2 (d)文獻[5]圖7 算例1的拓撲優化結果Fig.7 The topology results for example 1

圖8 優化結構邊緣剖切平面圖Fig.8 The sectional drawing of structure edge for topology results

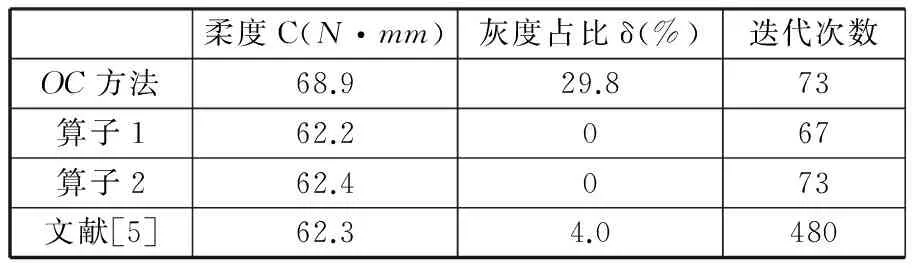
柔度C(N·mm)灰度占比δ(%)迭代次數OC方法68.929.873算子162.2067算子262.4073文獻[5]62.34.0480

由圖7可以看出，應用對比度增強算子的兩種方法抑制了灰度單元的出現，得到了拓撲結構清晰的優化結果。由圖8可以看出，與OC方法相比，應用對比度增強算子之后，得到了階躍型的結構邊緣。由表1可知，本文方法與OC方法相比，優化結果的柔度值更小，優化效果得到了提升；與文獻[5]中的灰度單元抑制方法相比，所得結果的灰度單元占比更小，優化結果更接近于0/1分布狀態，并且在優化求解效率方面占有明顯優勢。

算例2 圖9所示為一個簡支梁，尺寸為240 mm×60 mm，厚度為1 mm。上端面中間作用豎直向下的載荷F，大小為1 N。設計域體積的50%作為目標體積。鑒于是對稱結構，選用右側1/2模型進行優化計算，模型離散的數目為120×60。優化計算中采用了兩種過濾半徑進行過濾處理。圖10為優化結果的拓撲構型，其中圖10a、圖10c、圖10e采用的過濾半徑是2.5 mm，分別為OC方法、引入算子1和算子2的優化結果；圖10b、圖10d、圖10f采用的過濾半徑是4.5 mm，分別為OC方法、引入算子1和算子2的優化結果。各優化結果的柔度、灰度占比和迭代次數如表2所示。

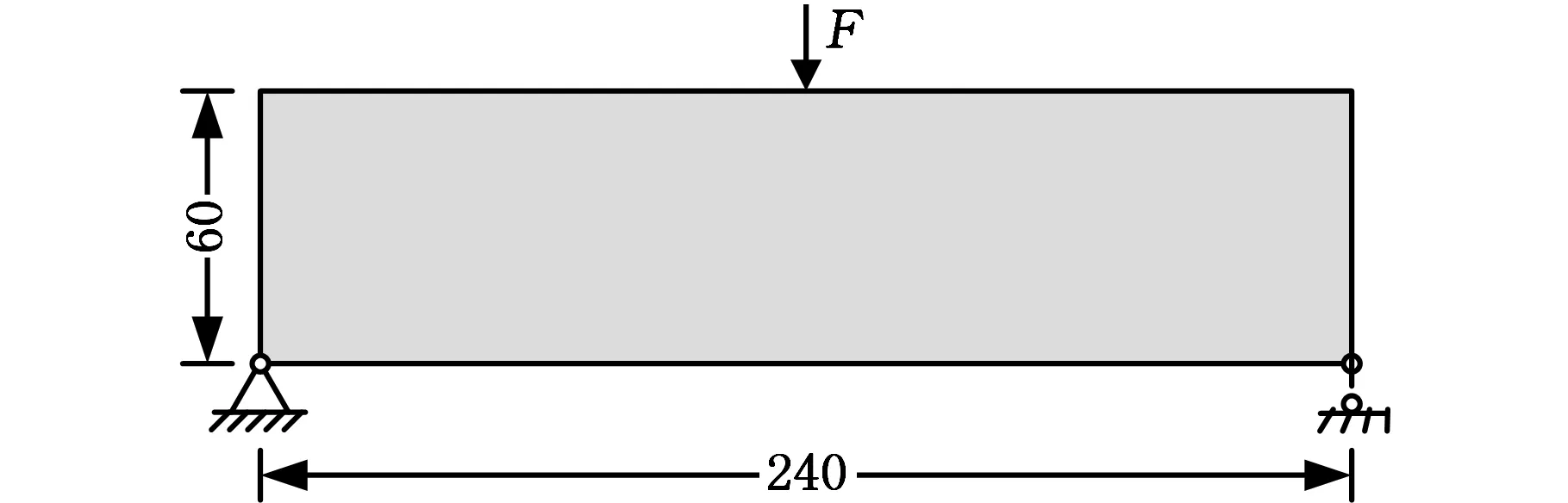
圖9 算例2設計域及邊界條件Fig.9 Design domain and boundary conditions of example 2

(a)OC方法(rmin=2.5 mm)(b)OC方法(rmin=4.5 mm)

(c)算子1(rmin=2.5 mm)(d)算子1(rmin=4.5 mm)

(e)算子2(rmin=2.5 mm)(f)算子2(rmin=4.5 mm) 圖10 算例2的拓撲優化結果Fig.10 The topology results for example 2

柔度C(N·mm)灰度占比δ(%)迭代次數圖10a81.922.5264圖10b86.429.861圖10c77.20.087圖10d78.00.068圖10e77.40.082圖10f78.20.078

由圖10可以看出，基于不同的過濾半徑，應用本文方法，都得到了結構邊緣清晰的優化結果，所得結果的拓撲形式與采用OC方法的一致，過濾半徑越大，所得結果中最小結構尺寸越大。該方法保持了過濾半徑控制優化結果中結構最小尺寸的優點。從表2中可以看出，在灰度方面，增大過濾半徑，會使OC法結果中的灰度增大，對本文方法沒有影響；在柔度方面，增大過濾半徑，會使優化結果的柔度值增大。

上述算例的結果顯示，所提出的兩種對比度增強算子得到的拓撲形態結果基本一致。這主要是因為對比度增強算子在拓撲結構主體框架形成之后才開始發揮作用，對比度增強算子對優化結果的拓撲形式幾乎不產生影響，主要作用是消除灰度單元、增強結構邊緣。算子1是逐步將靠近0-1兩極的密度進行增強，算子2是將中間密度向0-1兩極進行壓縮。在優化進程中，算子1穩步減少中間密度，在拓撲結構復雜的情況下往往能表現出更好的穩定性。

4 結論

本文提出了兩種形式的對比度增強算子，對優化準則法進行了修改，驅使中間密度向兩極分化，以抑制變密度法拓撲優化結果中灰度單元的出現。典型數值算例的計算結果顯示，該方法消除了過濾處理導致的邊緣擴散，得到了拓撲結構清晰的優化結果。

[1] BENDS?E M P. Optimal Shape Design as a Material Distribution Problem[J]. Structural Optimization, 1989, 1(4): 193-202.

[2] SIGMUND O, PETERSSON J. Numerical Instabilities in Topology Optimization: a Survey on Procedures Dealing with Checkerboards, Mesh-dependencies and Local Minima[J]. Structural Optimization, 1998, 16(1): 68-75.

[3] SIGMUND O. Design of Material Structures Using Topology Optimization[D]. Lyngby: Technical University of Denmark, 1994.

[4] BRUNS T E, TORTORELLI D A. Topology Optimization of Non-linear Elastic Structures and Compliant Mechanisms[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(26/27): 3443-3459.

[5] GUEST J K, PRéVOST J H, BELYTSCHKO T. Achieving Minimum Length Scale in Topology Optimization Using Nodal Design Variables and Projection Functions[J]. International Journal for Numerical Methods in Engineering, 2004, 61(2):238-254.

[6] SIGMUND O. Morphology-based Black and White Filters for Topology Optimization[J]. Structural and Multidisciplinary Optimization, 2007, 33(4): 401-424.

[7] XU S L, CAI Y W, CHENG G D. Volume Preserving Nonlinear Density Filter Based on Heaviside Functions[J]. Structural and Multidisciplinary Optimization, 2010, 41(4): 495-505.

[8] BORRVALL T, PERTERSSON J. Topology Optimization Using Regularized Intermediate Density Control[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(37/38): 4911-4928.

[9] GROENWOLD A A, ETMAN L F P. A Simple Heuristic for Gray-scale Suppression in Optimality Criterion-based Topology Optimization[J]. Structural and Multidisciplinary Optimization, 2009, 39(2): 217-225.

[10] 張志飛, 徐偉, 徐中明, 等. 抑制拓撲優化中灰度單元的雙重SIMP方法[J]. 農業機械學報, 2015, 46(11): 405-410.

ZHANG Zhifei, XU Wei, XU Zhongming, et al. Double-SIMP Method for Gray-scale Elements Suppression in Topology Optimization[J]. Transactions of The Chinese Society of Agricultural Machinery, 2015, 46(11): 405-410.

[11] 陳垂福, 楊曉翔. 一種考慮密度補償的變過濾半徑敏度過濾方法[J]. 中國機械工程, 2017, 28(6): 669-675.

CHEN Chuifu, YANG Xiaoxiang. Variable Filter Radius Sensitivity Filtering Method Considering Density Compensation[J]. China Mechanical Engineering, 2017, 28(6): 669-675.

[12] WANG M Y, ZHOU S, DING H. Nonlinear Diffusions in Topology Optimization[J]. Structural and Multidisciplinary Optimization, 2004, 28(4): 262-276.

[13] WANG M Y, WANG S. Bilateral Filtering for Structural Topology Optimization[J]. International Journal for Numerical Methods in Engineering, 2005, 63(13): 1911-1938.

AModifiedOptimalityCriterionMethodBasedonContrastEnhancementforGrayScaleSuppression

XU Xiaokui GUO Baofeng JIN Miao

Key Laboratory of Advanced Forging & Stamping Technology and Science,Yanshan University, Qinhuangdao,Hebei,066004

In order to suppress gray scale elements in density-based topology optimization, two kinds of contrast enhancement operators were proposed based on contrast enhancement strategy and introduced into the iterative calculation to modify the optimality criteria method. The contrast enhancement operator might enlarge the gray scale differences of the elements, drive the intermediate densities to the two ends of the range, and finally make the results convergence to the 0/1 material distribution. The effects of the proposed method were investigated with classical numerical examples. The results show that the optimization results with crisp boundaries are obtained by applying the proposed method.

topology optimization; contrast enhancement; gray element; optimality criteria method

2017-08-21

國家自然科學基金資助項目(51575474)；河北省自然科學基金資助項目(E2015203220)

TH122

10.3969/j.issn.1004-132X.2017.24.008

(編輯王艷麗)

許小奎，男，1990年生。燕山大學機械工程學院博士研究生。主要研究方向為成型設備結構分析與優化設計。郭寶峰(通信作者)，男，1958年生。燕山大學機械工程學院教授、博士研究生導師。E-mail: guobaofengysu@126.com。金淼，男，1968年生。燕山大學機械工程學院教授、博士研究生導師。