相似中的數學思想

文 /吳勝奎

相似中的數學思想

文 /吳勝奎

數學思想是數學知識的精髓.數學方法是數學思想的具體體現，是學習和運用數學知識解決問題的工具.現把相似中常見的數學思想歸納總結如下.

一、化歸與轉化思想

例 1如圖1，已知直線PT與⊙O相切于點T，直線PO與⊙O相交于A，B兩點．求證：PT2=PA·PB.

圖1

證明：連接OT，AT.

∵PT是⊙O的切線，∴PT⊥OT，

∴∠PTO=90°，∴∠PTA+∠OTA=90°，

∵AB是直徑，

∴∠ATB=90°，∴∠TAB+∠B=90°，

∵OT=OA，∴∠OAT=∠OTA，∴∠PTA=∠B，

在△PTA和△PBT中，

∵∠P=∠P，∠PTA=∠B，∴△PTA∽△PBT，

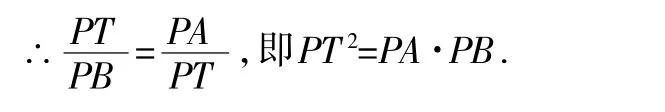
溫馨小提示：把證明線段成比例轉化為證明兩個三角形相似.這是處理比例線段最常見的方法.

二、分類討論思想

例 2 在△ABC中，AB=6，AC=5，點D在邊AB上，且AD=2，點E在邊AC上，當AE= 時，以A、D、E為頂點的三角形與△ABC相似．

溫馨小提示：分類要注意：一是正確選擇分類標準；二是分類要科學，既不重復又不遺漏.

三、方程和函數思想

例3一塊材料的形狀是銳角三角形ABC，邊BC=120mm，高AD=80mm，把它加工成正方形零件如圖2，使正方形的一邊在BC上，其余兩個頂點分別在AB，AC上．

（1）求證：△AEF∽△ABC；

（2）求這個正方形零件的邊長；

（3）如果把它加工成矩形零件，如圖3，問這個矩形的最大面積是多少？

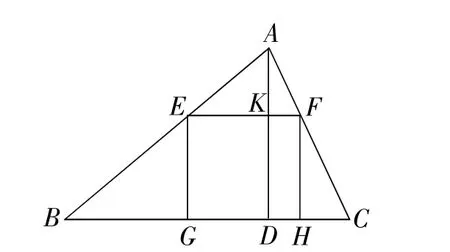
圖2

圖3

解：（1）∵四邊形EGHF為矩形，∴BC∥EF，

∴△AEF∽△ABC.

（2）設正方形零件的邊長為xmm，則KD=EF=x，AK=80-x，

∵△AEF∽△ABC，

答：正方形零件的邊長為48mm．

（3）如圖3，設EF=x，EG=y，∵△AEF∽△ABC，

當x=60時，此時矩形的面積最大，最大面積為2400mm2．

溫馨小提示：利用相似三角形的知識，構造出方程或函數，通過解方程或利用二次函數的性質求解.

王二喜