考慮不確定性故障的節點綜合脆弱性評估

李凌波，李華強，王羽佳，王蘭

（四川大學電氣信息學院，成都610065）

0 引 言

隨著電網各區域互聯日益加強，電力系統運行中發生的某些局部故障，可能會引發連鎖故障，進而擴大其范圍和程度，最后導致系統失穩、電網解列等重大事故，給系統帶來巨大經濟損失［1］。為實現電力系統的安全穩定運行，需對系統中重要的薄弱環節進行準確的定位，即對電力系統進行脆弱性分析。

目前，電力系統脆弱性研究主要分為狀態脆弱性和結構脆弱性兩方面［2］。狀態脆弱性基于運行參數篩選出運行狀態差的薄弱環節，主要研究方法有風險分析法、能量函數法［3-4］等；結構脆弱性基于網絡拓撲篩選出結構上比較重要的環節，主要研究方法有復雜網絡分析法等。文獻［5-6］基于風險理論，從脆弱源發生的概率及后果兩方面分析，將風險理論應用于電網的脆弱性評估中。其結合風險的脆弱性評估有效克服了確定性方法的不足，但沒有具體到節點的脆弱性風險評估。文獻［7］從節點的靜態能量角度出發，提出趨勢指標來篩選系統的脆弱節點。文獻［8］提出能量裕度指標并應用其對脆弱支路進行篩選。上述基于能量函數的脆弱性評估，是從裕度或靈敏度單一因素考慮的。實際上，狀態脆弱性應同時考慮裕度和靈敏度兩方面。

單一的脆弱性指標可從某個方面反映系統的脆弱性特征，不同的脆弱性指標可從不同的角度描繪系統的脆弱性。要準確、合理的篩選系統的脆弱節點，指標需滿足：（1）指標可以反映出系統在正常狀態下的脆弱節點；（2）指標可以反映出在故障擾動下，節點承受擾動沖擊的能力；（指標可以反映出節點在網絡中的重要程度。

本文基于節點的靜態能量函數模型，綜合考慮能量裕度和靈敏度建立節點狀態脆弱性因子用以反映指標要求（1）；考慮系統中事故的不確定性，應用風險理論計算節點承受故障沖擊的能力，本文以低電壓風險表示，并定義為脆弱性風險因子用以反映指標要求（2）；以電氣介數模型建立節點的結構脆弱性因子，用以反映指標要求（3）。綜合以上因素，建立節點的綜合脆弱性評估模型，全面準確的定位系統的薄弱節點。利用MATLAB軟件編程，應用于IEEE-30母線系統，通過無功補償的驗證，說明本文所提脆弱性評估方法的有效性。

1 節點狀態脆弱性

節點到達臨界能量的快慢不僅與能量裕度還與靈敏度因素有關。因此，節點狀態脆弱性從裕度和靈敏度兩方面來分析。

1.1 節點能量函數模型

電力系統中，節點i的靜態能量函數為［9］：

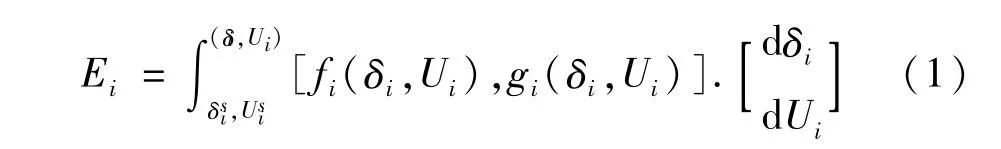
式中 fi（δi，Ui）、gi（δi，Ui）分別表示節點的有功、無功平衡方程，（δi，Ui）表示初始負荷水平下節點的電壓相角與幅值表示當前負荷水平下節點i的電壓相角與幅值。

1.2 節點能量靈敏度因子

分析節點能量與電壓之間的變化規律，節點的脆弱靈敏度因子定義如下：

α（i）為節點能量對電壓幅值的變化趨勢，可反映節點在不同運行狀態下的堅強程度。α（i）值越小，說明節點電壓水平惡化速度越快，其對負荷增長的耐受能力越弱，表現出更為明顯的脆弱性。

1.3 節點能量裕度因子

節點能量裕度定義如下：

式中 E、E0、Ecr分別表示節點能量的當前值、初始值與臨界值（系統崩潰點對應的能量值）。脆弱裕度越小，表明節點當前能量值與其臨界能量的距離越近。

1.4 節點狀態脆弱性指標

綜合考慮能量裕度與靈敏度，建立節點的狀態脆弱性評估指標：

狀態脆弱性指標越小，表明節點更易受外界擾動的影響，電壓更接近極限崩潰點，表現出更強的脆弱性。

2 節點脆弱性風險評估

考慮到不確定性故障對節點脆弱性評估的影響，本文在考慮故障因素時，基于風險來評估系節點的脆弱性。節點潛在的脆弱性通過電壓越限風險大小來表示。電壓越限風險越大，則節點越脆弱，更易由于電壓越限導致嚴重事故發生［10-11］。

2.1 基于運行可靠性的故障概率模型

線路停運概率模型隨系統運行狀態變化而變化。文章采用計及線路潮流的故障模型，確定時變運行狀態下元件的故障概率。

線路故障概率受線路潮流影響，線路潮流在正常范圍內時，線路的故障概率很低；當線路潮流增加時，輸電線路發熱量增加，逐漸失去機械強度，溫度持續上升，可能超過線路熱穩定極限，其故障概率大幅增加，故障概率模型如圖1所示［12］。

圖1 線路故障概率模型Fig.1 Probability model of line fault

（1）當支路的潮流在正常值范圍內時，線路的停運概率受潮流的影響很小，取線路的停運概率的長期統計平均值：

（2）當線路的潮流大于等于線路極限Lmax時，線路的停運概率為1：

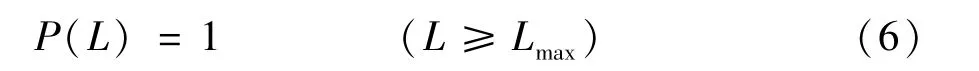
（3）當線路的潮流值在線路正常值與極限值之間時，線路因發熱而熔斷或者因保護裝置動作而被切除的概率隨線路的潮流的增加而增大，為簡化計算，用折線模型來表示：

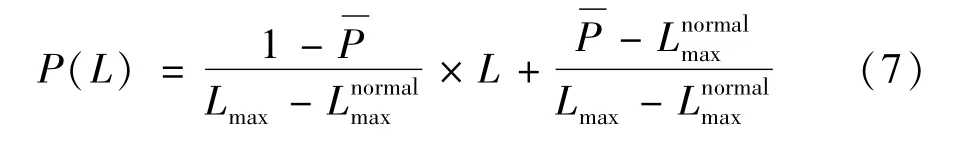
2.2 節點低電壓嚴重度函數

低電壓嚴重度呈偏小型分布，如圖2所示［13］。

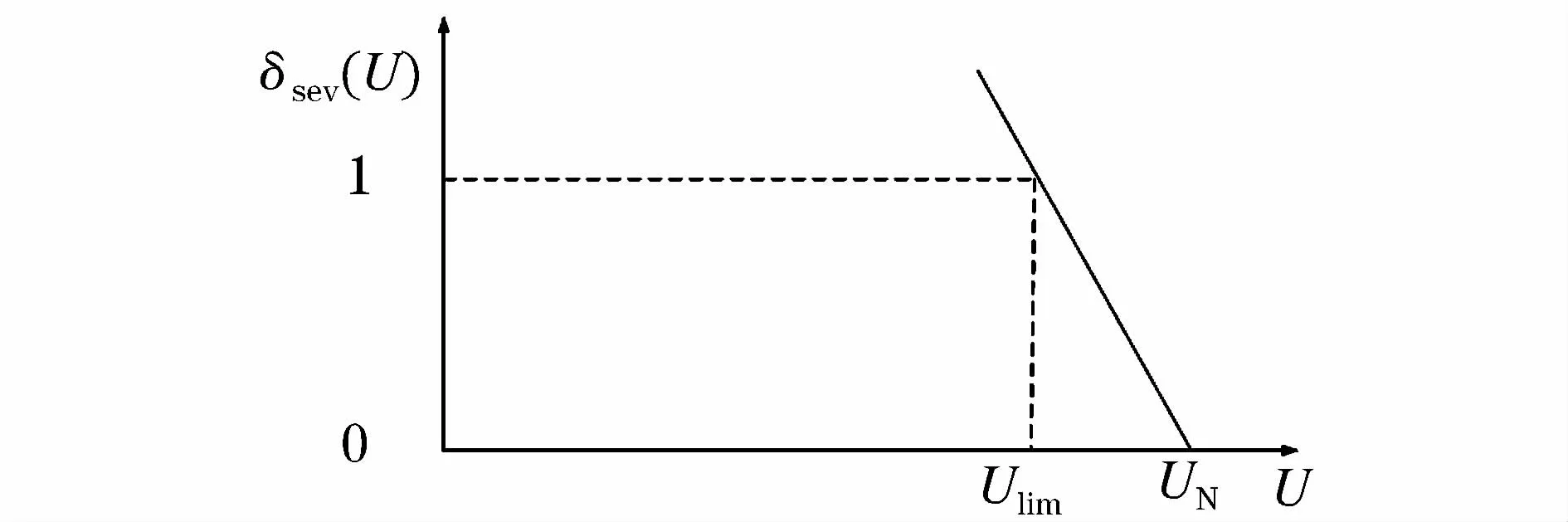
圖2 低電壓嚴重度函數Fig.2 Severity function of low voltage

對應節點i的低電壓嚴重度函數可表示如下：

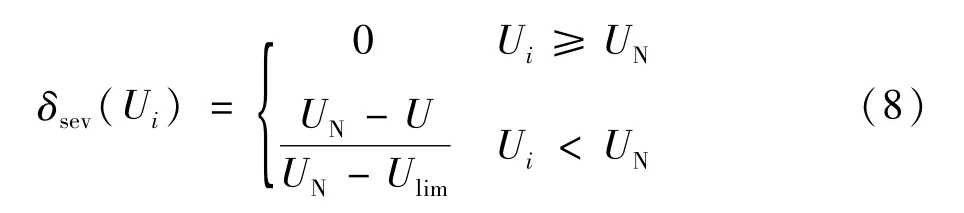
式中Ui為節點i當前的運行電壓；UN為節點電壓額定值；Ulim為設定的低電壓最大風險閾值，一般情況下可取為額定電壓的90%。

2.3 節點的脆弱性風險評估

風險可表示為所研究狀態出現的概率與其后果的乘積。第j個狀態下節點i的電壓越限風險，計算方法如下：

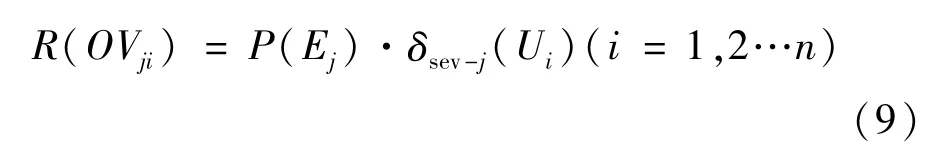
式中 n代表節點個數；P（Ej）表示狀態發生的概率；δsev－j表示j狀態下節點的低電壓嚴重度。

將所有不同狀態的R（OVji）累加，可以獲得在所有N－1事故下節點的電壓越限風險總值即節點i的脆弱性風險因子：

式中m代表事故的總數量。

R（OVi）越大，節點發生低電壓的風險越大，表示節點承受故障擾動的能力越弱，即節點潛在的風險越大，節點越脆弱。

3 節點結構脆弱性

在復雜網絡理論中，電氣介數可以描繪“發電機-負荷”之間潮流傳輸對節點的利用情況，體現節點在電力系統潮流傳輸中的重要程度。可用來表征由網絡拓撲所決定的節點結構脆弱性。

節點i的電氣介數定義如下［14］：

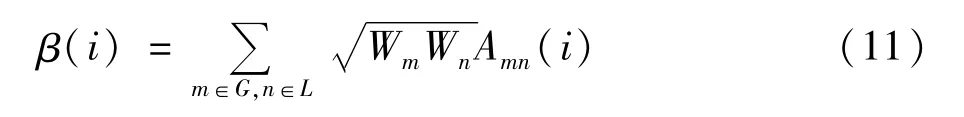
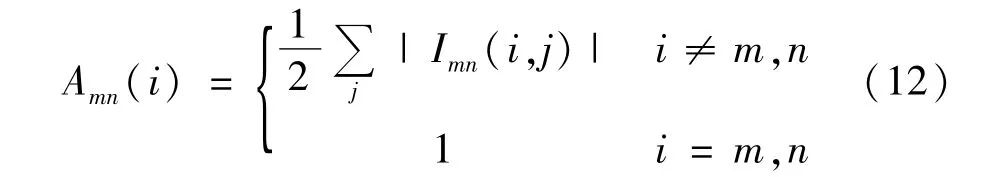
式中G、L依次代表電網中發電機、負荷節點集合；Wm表示發電機節點m的權重系數，一般取其實際出力或額定容量；Wn表示負荷節點n的權重系數，一般取其實際負荷量或峰值負荷；Amn表示在節點m、n間加單位電流后，此時節點i的電氣介數；Imn（i，j）表示向“發電機-負荷”節點對（m，n）之間加單位電流元后，線路i－j上的電流值；j表示與i直接相連的所有節點。

β（i）表示節點在電力系統潮流傳輸中的貢獻度。β（i）越大，節點在網絡拓撲中越重要，即節點的結構脆弱性越大。

4 節點綜合脆弱性

綜合考慮以上因素建立節點綜合脆弱性指標：

式中 λ（i）、R（OVi）、β（i）分別為節點狀態脆弱因子、脆弱風險因子和結構脆弱因子，ω1、ω2、ω3分別為其在節點脆弱性評估中所占的權重，且ω1＋ω2＋ω3＝1。

狀態脆弱因子可甄別從運行狀態來說比較脆弱的節點，脆弱性風險因子考慮了系統中不確定性故障對節點脆弱性評估的影響，結構脆弱因子可衡量節點在網絡拓撲中的重要度，即結構層面的脆弱性。本文所建立的節點綜合脆弱性指標旨在把三者結合起來，篩選出在系統中運行狀態差、受不確定性故障影響較大且在拓撲結構上比較活躍的脆弱節點，以便運行人員及時采取有效防控措施。

5 算例仿真

選用IEEE-30標準母線系統進行仿真分析，該系統包括6臺發電機、41條支路。利用牛頓-拉夫遜算法計算初始負荷下的電網潮流，運用連續潮流法計算不同負荷下的節點各脆弱因子指標。通過在不同脆弱性的節點處進行相同量的無功補償，對比分析系統狀態的改善效果，驗證所提評估方法的正確性。

5.1 節點的脆弱性分析

5.1.1 節點的狀態脆弱性分析

根據仿真分析，各節點的狀態脆弱因子如圖3所示。由圖可見，節點 14、13、15、16、29的狀態脆弱因子相對較小，說明從狀態上分析是比較脆弱的節點。分析仿真數據可以發現，節點14、13、15、16的能量靈敏度比較小，說明其電壓水平隨負荷水平的增加，弱化趨勢比較深；節點29的能量裕度比較小，在狀態脆弱性排序中也比較靠前。可見，所建立的綜合考慮能量靈敏度和裕度的狀態脆弱因子可以更全面的反映節點基于運行狀態的脆弱性。

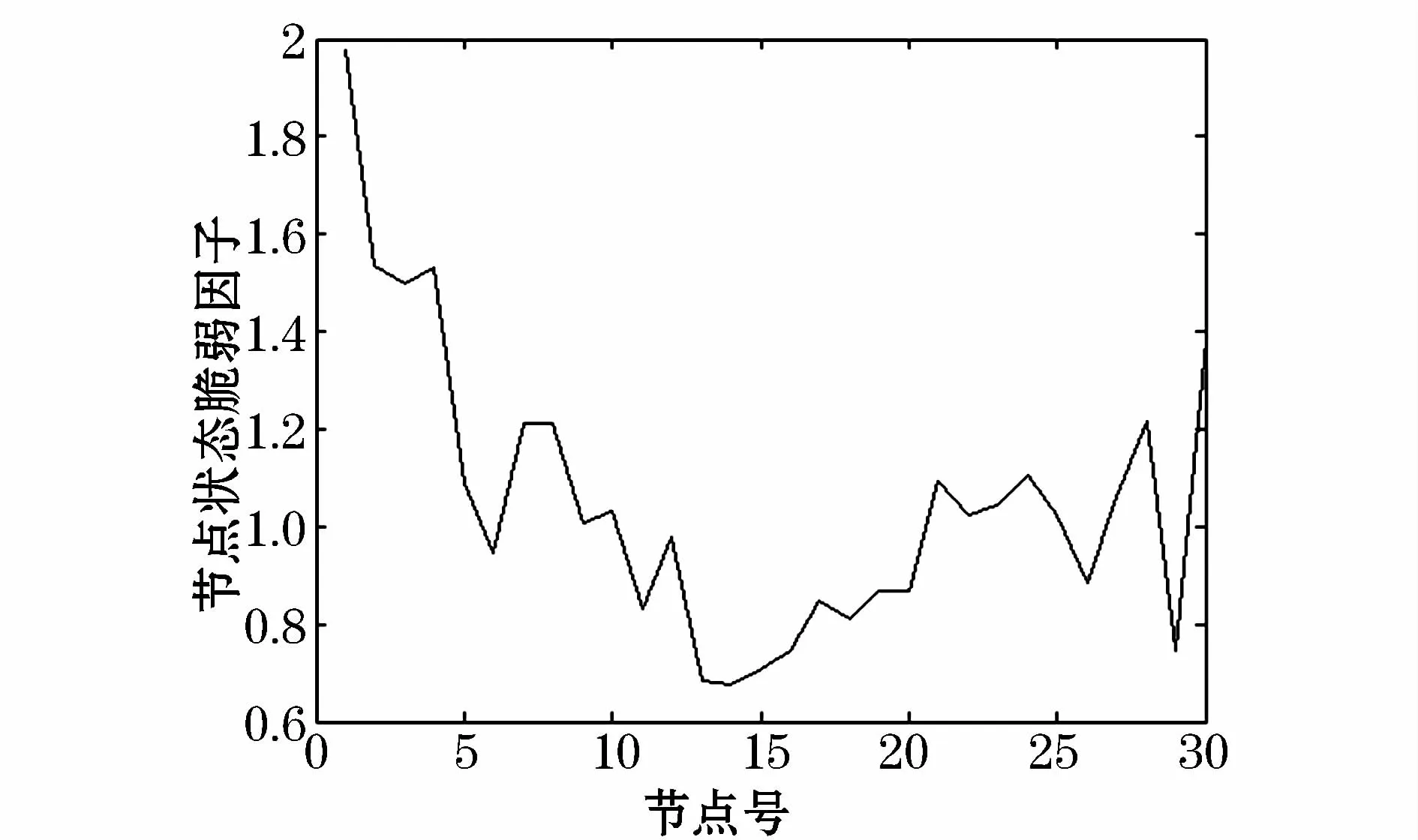
圖3 節點的狀態脆弱因子曲線Fig.3 Curve of node vulnerability factor

5.1.2 考慮不確定性故障的節點脆弱性風險分析

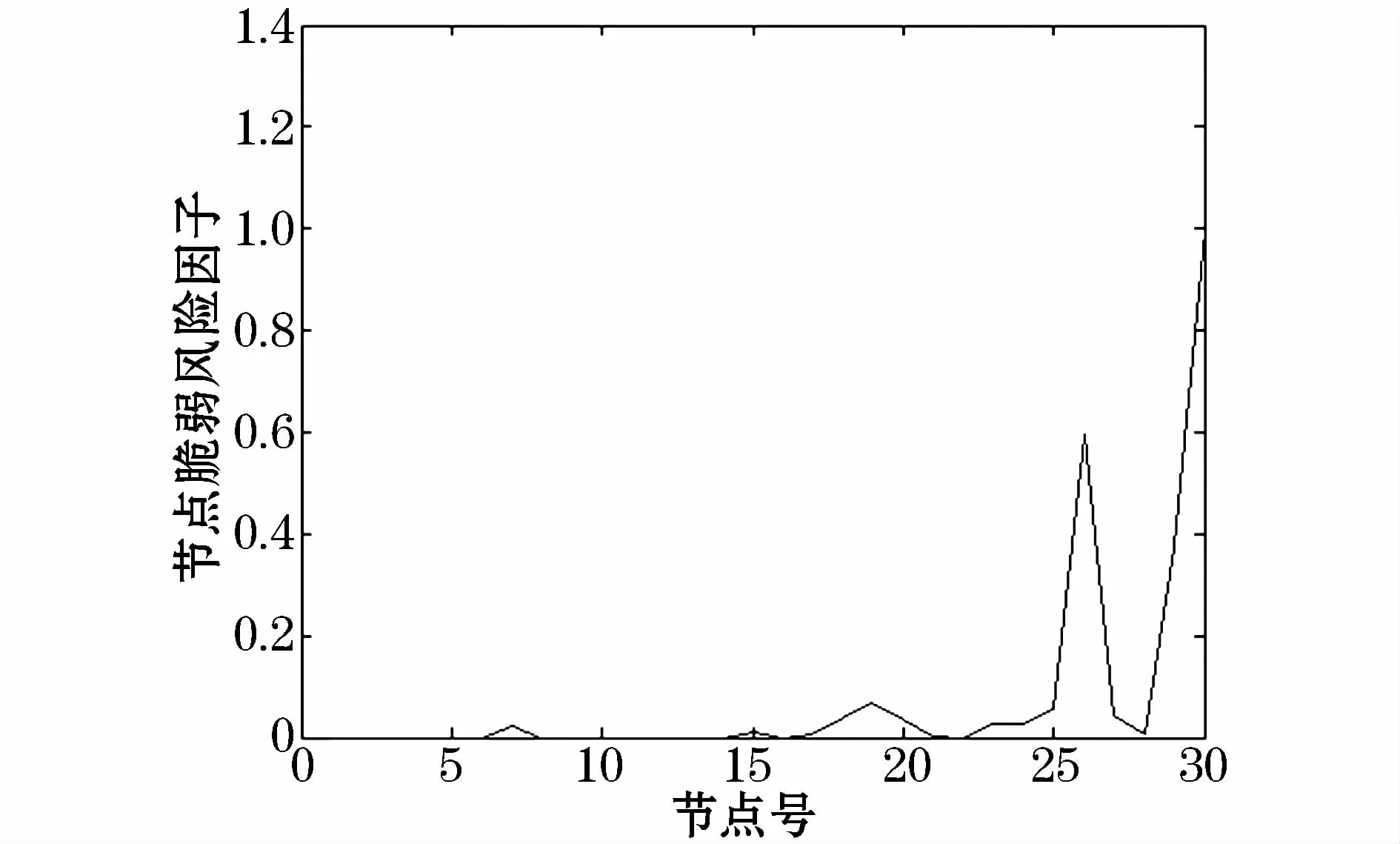
圖4 節點的脆弱性風險因子曲線Fig.4 Curve of node vulnerability risk factor

由圖可以看出，節點 30、26、29、19、25、的脆弱性風險因子相對較大，說明其受不確定性故障影響比較大，比較容易出現低電壓問題，即潛在的低電壓風險比較大。因此，不確定性故障擾動的影響也是脆弱節點篩選需考慮的因素之一。

5.1.3 基于電氣介數的節點結構脆弱性分析

電氣介數可以反映節點在網絡拓撲中的活躍程度即節點的重要度，基于電氣介數的結構脆弱因子仿真結果如圖5所示。

圖5 節點的結構脆弱因子曲線Fig.5 Curve of structure vulnerability factors of nodes

由仿真結果可以看出，節點6、4、10、2、12的結構脆弱因子相對較大，說明其在網絡拓撲結構中比較重要。通過分析IEEE-30系統的拓撲圖可以發現，節點6、4、12為發電機 1、2、5、8、13與系統聯絡即進行功率傳輸的關鍵節點；節點10居于網絡中央位置，連接六條支路，是功率輸送的關鍵節點；發電機節點2的有功出力最大，在系統中起著調壓與功率平衡的重要作用，因此其重要性也比較突出。

5.1.4 節點的綜合脆弱性分析

將狀態脆弱因子、脆弱性風險因子和結構脆弱因子有效結合，得到節點的綜合脆弱性評估指標，其不僅兼顧了節點的運行狀態、在系統中的重要程度，還考慮了系統的不確定性故障擾動對脆弱節點篩選的影響。取ω1＝ω2＝ω3＝1／3，節點的綜合脆弱性指標仿真結果如圖6所示。

圖6 節點的綜合脆弱性指標曲線Fig.6 Index curve of node comprehensive vulnerability

由圖可看出，節點6、15、29、30、26的綜合脆弱性指標相對較大，說明這些節點比較脆弱。由之前的各個脆弱因子分析可知，節點6的結構脆弱性因子比較大，即結構上比較重要；節點15、29屬于狀態脆弱性比較大的節點；節點30、26的脆弱性風險比較大。由此可見，本文構建的綜合脆弱性指標可以反映綜合考慮狀態、結構和不確定性故障影響因素下的脆弱節點。

5.2 與傳統方法對比

傳統方法中［9］，基于運行狀態和結構脆弱性構建了節點的綜合脆弱度指標，通過仿真分析篩選出比較脆弱的節點為 6、10、12、2、15，其中，6、10、12、2是結構脆弱性比較大的節點，15是狀態脆弱性比較大的節點。應用本文所建立的綜合脆弱性指標篩選出比較脆弱的節點為6、15、29、30、26，其中，6是結構脆弱性比較大的節點，15、29是狀態脆弱性比較大的節點，30、26是脆弱風險比較大的節點。可以發現兩個結果稍有不同，這是因為：

（1）在狀態脆弱性指標的構建上，不僅考慮了能量靈敏度因子還考慮了能量裕度的影響；

（2）在考慮狀態和結構脆弱性的基礎上，本文還考慮了不確定性因素的影響，即考慮故障的不確定性，節點發生低電壓的潛在風險比較大，那么節點同樣會比較脆弱。因此，應用本文的方法可以篩選出脆弱性風險比較大的節點30、26。

5.3 綜合脆弱性指標的驗證

為驗證本文所提綜合脆弱性評估方法的正確性和實用性，根據節點的綜合脆弱性排序結果，選擇具有代表性的三個節點：節點6（最脆弱）、節點19（相對堅強）、節點1（比較堅強），分別進行相同量的無功補償，然后對補償效果進行對比分析，結果見表1。

表1 補償前后節點1-10的綜合脆弱性指標Tab.1 Comprehensive vulnerability index of node 1-10 before and after compensation

通過對比分析可以看出，在節點6處進行無功補償效果是最好的，節點19居中，在節點1處補償的效果最不好。上述仿真結果說明，在所選擇的最脆弱的節點處進行無功補償對系統的改善是最佳的，驗證了所提節點綜合脆弱性評估方法的正確性和實用性。

6 結束語

與傳統脆弱性評估方法相比，改進如下：

（1）加入了能量裕度因子，對狀態脆弱指標進行改善，建立了綜合考慮能量靈敏度和裕度的狀態脆弱性指標；

（2）定義了節點的脆弱性風險因子指標以表示節點脆弱性受不確定性故障擾動的影響；

（3）綜合考慮節點的狀態脆弱性、脆弱性風險因子和結構重要度，建立了節點的綜合脆弱性評估模型，克服了傳統評估方法中沒有考慮系統不確定性故障因素的不足。

所提的節點脆弱性評估指標綜合考慮了狀態、不確定性故障和結構因素，評估結果更切合實際，可全面準確的定位系統的脆弱節點，為工程應用提供合理參考。