基于Copula理論和切片采樣技術(shù)結(jié)合拉丁超立方抽樣的概率潮流計算*

毛曉明，葉嘉俊，魏煥政，李牧星

（廣東工業(yè)大學(xué)自動化學(xué)院，廣州510006）

0 引 言

電力系統(tǒng)存在大量的隨機性因素，隨著風(fēng)、光等可再生能源發(fā)電大規(guī)模并網(wǎng)，不確定性因素進一步增加［1-3］。Borkowska于 1974年提出的概率潮流（Probabilistic Load Flow，PLF）分析方法通過計算節(jié)點電壓、線路功率及網(wǎng)損率的期望、方差、概率密度函數(shù)（Probability Density Function，PDF）及累積分布函數(shù)（Cumulative Distribution Function，CDF）等，掌握系統(tǒng)穩(wěn)態(tài)運行的概率統(tǒng)計特性［4］。

PLF計算方法有多種。其中，MCS方法雖有計算效率低等不足，但仍被認(rèn)為是最強大、最靈活和最準(zhǔn)確的PLF分析方法［5］。針對MCS的不足，人們將馬爾科夫過程（Markov Process，MP）引入到MCS中，形成了馬爾科夫鏈蒙特卡洛（Markov Chain Monte Carlo，MCMC）模擬法［6-7］。可是，廣泛用于構(gòu)建馬爾科夫鏈的Metropolis-Hastings算法和Gibbs算法也存在如下不足：（1）Metropolis-Hastings算法需先指定一個便于隨機數(shù)生成的“建議”分布函數(shù)，而給復(fù)雜的分布函數(shù)指定一個合適的“建議”分布函數(shù)是很困難的；（2）Gibbs算法需要先確定參數(shù)的滿條件分布，但滿條件分布復(fù)雜的變量無法直接采樣。這些缺點限制了MCMC方法的廣泛使用。

針對上述問題，文獻［8］將切片采樣（Slice Sampling，SS）技術(shù)［9］引入到電力系統(tǒng) PLF中，提高了傳統(tǒng)MCMC方法的計算精度及效率。本文在文獻［8］的基礎(chǔ)上，進一步引入Copula理論和拉丁超立方抽樣，以計及輸入變量間的相關(guān)性并提高計算效率，形成 CMCMCS-CI（Correlation Slice Sampling MCMC Simulation with Copula and Improved Latin Hypercube Sampling）算法。新方法采用Kendall秩相關(guān)系數(shù)度量隨機變量的相關(guān)程度，采用切片采樣的MCMC算法和Copula理論實現(xiàn)相關(guān)隨機變量初始樣本的采樣，采用改進的拉丁超立方采樣對初始樣本進行處理，降低樣本規(guī)模，在考慮隨機變量相關(guān)性的同時，進一步提高MCMC方法的計算效率。以改造后的IEEE-14節(jié)點測試系統(tǒng)為算例，驗證了所提方法的準(zhǔn)確性和有效性，在此基礎(chǔ)上研究風(fēng)、光出力相關(guān)性對電力系統(tǒng)概率潮流的影響。

1 Copula理論

通常由隨機變量的聯(lián)合分布可以方便地確定各自的邊緣分布，但由隨機變量的邊緣分布卻很難確定其聯(lián)合分布。Copula理論的提出和完善，一定程度上解決了這一問題［10］，本文采用該理論來建立潮流計算中隨機關(guān)聯(lián)性變量的概率分布模型。

1.1 Copula理論簡介

Copula理論認(rèn)為一個N維聯(lián)合分布函數(shù)可以分解為N個邊緣分布函數(shù)和一個連接Copula函數(shù)，且變量間的相關(guān)關(guān)系可由這個連接函數(shù)表示［11］。Nelsen于2006年給出了 Copula函數(shù)的嚴(yán)格定義［12］：Copula函數(shù)是將隨機向量X1，X2，…，XN的聯(lián)合分布函數(shù) F（x1，x2，…，xn）與各自邊緣分布函數(shù) FX1（x1），F(xiàn)X2（x2），…，F(xiàn)XN（xn）相連接的連接函數(shù)，即存在函數(shù)C（u1，u2，…，un）使：

Copula函數(shù)種類多樣［13］，其中阿基米德Copula函數(shù)具有優(yōu)良的性質(zhì)，已廣泛應(yīng)用于各個領(lǐng)域。

1.2 Copula函數(shù)的相關(guān)性測度

隨機變量間相關(guān)性度量的方法有很多，Kendall秩相關(guān)系數(shù)τ有諸多優(yōu)點［14］，本文選取Kendall秩相關(guān)系數(shù)。

設(shè)（x1，y1），（x2，y2）是二維隨機向量（X，Y）的 2個觀測值，如果（x1-x2）（y1-y2）＞0，則稱（x1，y1）和（x2，y2）是和諧的（concordant）；若（x1-x2）（y1-y2）＜0，則稱它們是不和諧的（discordant）。

設(shè)（X1，Y1），（X2，Y2）是相互獨立且與（X，Y）同分布的二維隨機向量，則Kendall秩相關(guān)系數(shù)τ定義為：

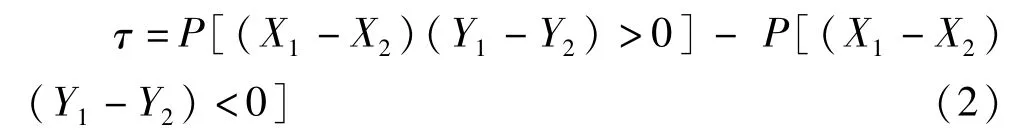
式中 P［（X1-X2）（Y1-Y2）＞0］、P［（X1-X2）（Y1-Y2）＜0］分別表示和諧及不和諧的概率。τ∈［-1，1］。τ∈［-1，0）、τ＝0和 τ∈（0，1］分別表示隨機變量負相關(guān)、不能確定相關(guān)關(guān)系及正相關(guān)。

Kendall秩相關(guān)系數(shù)τ可由Copula函數(shù)計算得到。例如，若隨機變量w1和 w2的 Copula函數(shù)為C（F1（w1），F(xiàn)2（w2）），則 τ可由下式得到［13］：

2 采樣算法

2.1 切片采樣算法

切片采樣是一種廣義的Gibbs采樣算法，在構(gòu)造可逆馬爾科夫轉(zhuǎn)移核時要先預(yù)定義一個恒定分布［15］。欲從集合Rn中抽取服從某個概率分布的變量x，且其概率密度函數(shù) g（x）與某一函數(shù) f（x）成正比，我們可以通過對g（x）曲線下方的（n+1）維空間隨機均勻采樣得到。

引入附加變量y，定義關(guān)于x和y的聯(lián)合分布，其中y在曲線 f（x）下的區(qū)域為 U＝｛（x，y）：0＜y＜f（x）｝，則（x，y）的聯(lián)合概率密度函數(shù) f（x，y）可以表示為［9］：

式中Z＝∫f（x）d x。變量x的邊緣密度函數(shù)為：

對（x，y）進行抽樣，然后消去附加變量y即得到變量x的樣本。具體迭代步驟為：

（1）從區(qū)間（0，f（x0））隨機均勻生成 y，其中 x0為給定的初值，切片S（由y來定義）對應(yīng)的橫軸x值的集合為｛x：f（x）＞y｝；

（2）確定以x0為擴張基點且覆蓋S絕大部分區(qū)間的采樣區(qū)間 I＝（L，R）；

（3）從區(qū)間I均勻隨機地生成新變量x1。

單變量切片采樣算法的示意圖如圖1所示。圖中由y確定的水平切片S被曲線f（x）分割成許多小切片 S1、S2、S3，且與 S對應(yīng)的橫軸 x值均滿足f（x）＞y；以x0為基點的樣本區(qū)間擴張到S外的區(qū)域前，寬度以w為步長持續(xù)增加，然后在擴張后的樣本區(qū)間I＝（L，R）均勻隨機地生成新變量 x1。

圖1 單變量概率密度函數(shù)的切片采樣算法實現(xiàn)示意圖Fig.1 Single-variable slice sampling by simulating a sample from the region under its density function

由于函數(shù)f（x）的起伏會把水平切片S切割成許多小切片，使區(qū)間I呈現(xiàn)多重邊界，且有些概率密度模型很復(fù)雜，因此如何確定采樣區(qū)間成為切片采樣最棘手的問題。

針對這種情況，Neal提出了“Stepping-out”和“Shrinkage”算法來確定區(qū)間I的邊界。首先，以x0為基點定義一寬度為w的微型水平區(qū)間I。然后以w為步長重復(fù)擴張區(qū)間I，直到該區(qū)間超出水平切片S的范圍，即 f（x）≤y。由于采樣區(qū)間 I＝（L，R）對應(yīng)的橫軸x值不一定全部滿足f（x）＞y，所以若新生成的隨機數(shù)x1位于切片S外部，則收縮區(qū)間I兩端，然后再次生成x1，重復(fù)此過程直到生成的x1滿足f（x1）＞y為止。隨著不滿足條件的隨機變量不斷被拒絕及區(qū)間I的收縮，符合條件的隨機數(shù)x1的生成概率逐漸增加。詳細步驟見文獻［9］。

通過與Gibbs算法類似的采樣方式（即：將每個變量的分布函數(shù)當(dāng)作條件性依賴于其它變量當(dāng)前值的單變量概率模型）對不同變量輪流依次采樣即可實現(xiàn)對多元分布概率模型的采樣。

將該算法應(yīng)用于PLF中，可改善采樣值在隨機變量分布中的覆蓋程度、提高樣本采樣效率，并顯著提高傳統(tǒng)MCMC方法的計算準(zhǔn)確度［8］。

2.2 改進的拉丁超立方采樣方法

傳統(tǒng)的拉丁超立方采樣（Latin hypercube sampling，LHS）［16］在對隨機變量 w進行采樣時，需要知道隨機變量的CDF表達式。但在很多情況下，w的CDF是未知或難以求取的，這就限制了LHS的應(yīng)用。針對這一不足，文獻［17］提出了一種基于離散數(shù)據(jù)的改進拉丁超立方采樣方法（ILHS），該方法只需依賴于隨機變量的CDF特性。

對于單個輸入隨機變量w1，在已知n個離散數(shù)據(jù) W1×n＝［w1，w2，…，wn］的情況下，W1×n中任意樣本發(fā)生的概率為1／n。如果將w1的邊際累積分布函數(shù)均勻地分割成N個互不重疊的區(qū)間，那么每個區(qū)間包含 n／N個離散數(shù)據(jù)，則樣本 W?1×N＝［w?1，w?2，…，w?N］（N≤n）可以通過下列步驟得到：

（1）將離散數(shù)據(jù)W1×n由小到大進行排序，得到向量 W′1×n＝［w′1，w′2，…，w′n］；

（2）將向量 W′1×n的第 i個元素 w′i賦值給向量W″1×N的第 k（k＝1，2，…，N）個元素 w″k，即 w″k＝w′i，其中i與k的關(guān)系如式（6）所示：

（3）對樣本 W″1×N＝［w″1，w″2，…，w″N］進行隨機排序，即可得到樣本 W?1×N＝［w?1，w?2，…，w?N］。

對于 m維輸入隨機變量向量 Wm×1＝［w1，w2，…，wm］T，在已知n組離散數(shù)據(jù) Wm×n＝［w1，w2，…，wm］T（wj＝［wj1，…，wjn］，j＝1，2，…，m）的情況下，可由下列步驟得到相應(yīng)的LHS樣本矩陣Wm×N：

（1）采用單變量的ILHS方法對輸入隨機變量w1的n個離散數(shù)據(jù)w1＝［w11，…，w1n］進行采樣，獲得樣本 w?1＝［w?11，w?12，…，w?1-N］；

（2）計算變量 w1的樣本 w?1的第 i（i＝1，2，…，N）個元素 w?1（i）在 w1＝［w11，…，w1n］的位置參數(shù)li，即 w?1（i）＝w1（li）；

（3）對于 Wm×1＝［w1，w2，…，wm］T的第 h（h＝2，…，m）個變量 wh，ILHS采樣得到的樣本為 w?h＝［w?h1，w?h2，…，w?hN］，其中 w?h的第 i個元素 w?h（i）為 wh＝［wh1，wh2，…，whN］的第 li個元素 w″h（li），即w?h（i）＝w″h（li）；

（4）重復(fù)步驟（3）即可得到所有隨機變量的LHS采樣樣本，從而得到隨機變量向量Wm×1的樣本矩陣W?m×N＝［w?1，w?2，…，w?m］T（w?i＝［w?i1，w?i2，…，w?iN］，i＝1，2，…，m）。

步驟（3）確保了樣本矩陣 W?m×N中隨機變量的相關(guān)性與Wm×n中隨機變量相關(guān)性的一致。

將ILHS應(yīng)用于SS生成的初始樣本中，在保證隨機變量相關(guān)性的同時，進一步減小PLF的計算樣本的規(guī)模，進一步提高MCMC方法的計算效率。

3 基于CMCMCS-CI采樣的概率潮流計算方法

生成滿足相關(guān)性及邊緣分布等要求的輸入隨機變量的樣本，是基于CMCMCS-CI采樣的概率潮流計算方法的關(guān)鍵。根據(jù)生成的樣本通過潮流方程式（7）計算得到系統(tǒng)節(jié)點電壓D及支路潮流H的值。

式中W節(jié)點注入功率向量；D為節(jié)點電壓狀態(tài)向量；H為支路輸出功率向量；f和g分別為節(jié)點功率和支路潮流方程。

具體步驟如下：

（1）輸入基礎(chǔ)數(shù)據(jù)，包括配電網(wǎng)結(jié)構(gòu)參數(shù)、節(jié)點注入功率 Wm×1＝［w1，w2，…，wm］T及采樣規(guī)模N等；

（2）根據(jù)節(jié)點注入功率Wm×1間的相關(guān)關(guān)系選擇合適的Copula函數(shù)描述其相關(guān)結(jié)構(gòu)；

（3）根據(jù)選擇的Copula函數(shù)采用切片采樣算法采樣得到注入功率 Wm×1初始樣本矩陣 Wm×n＝［w1，w2，…，wm］T（wj＝［wj1，…，wjn］，j＝1，2，…，m）；

（4）采用ILHS方法對初始樣本矩陣 Wm×n進行采樣獲得最終樣本矩陣 W?m×N＝［w?1，w?2，…，w?m］T（w?i＝［w?i1，w?i2，…，w?iN］，i＝1，2，…，m）；

（5）將N組節(jié)點注入功率Wm×1的采樣值分別帶入式（7）依次采用牛頓-拉夫遜算法進行N次確定性潮流計算，獲得N組節(jié)點電壓、支路潮流等輸出隨機變量的計算值；

（6）應(yīng)用統(tǒng)計學(xué)的方法統(tǒng)計節(jié)點電壓、支路潮流等輸出隨機變量的數(shù)字特征和概率分布。

4 考慮相關(guān)性的風(fēng)-光聯(lián)合出力模型

本文建立風(fēng)電場及光伏電站聯(lián)合出力模型，研究高比例風(fēng)、光并網(wǎng)對電力系統(tǒng)概率潮流的影響。

4.1 風(fēng)力發(fā)電出力概率模型

研究表明，世界上大部分地區(qū)風(fēng)速和風(fēng)電場有功輸出滿足線性關(guān)系［18］，即風(fēng)電場出力Pw的累積分布函數(shù)F（pw）和概率密度函數(shù)f（pw）可表示為：

式中風(fēng)電場風(fēng)速 v服從Weibull分布，且k、c分別代表Weibull分布的形狀參數(shù)和尺度參數(shù)；k1＝Pr／（vr-vci）；k2＝-k1vci；Pr、vci、vr分別表示風(fēng)電場的額定輸出功率、切入風(fēng)速和額定風(fēng)速。

4.2 光伏發(fā)電出力概率模型

據(jù)統(tǒng)計，世界上絕大部分地區(qū)的光伏輸出功率ppv的概率密度函數(shù) f（ppv）和累積分布函 F（ppv）數(shù)可表示為［2］：

式中Γ表示Gamma函數(shù)；α、β分別表示Beta分布的形狀參數(shù)；ppv、pmax分別表示光伏電站的實際和最大有功出力。

4.3 考慮相關(guān)性的風(fēng)-光電場聯(lián)合出力模型

本文關(guān)注的是風(fēng)、光電場出力特性對電力系統(tǒng)概率潮流的影響，故風(fēng)電場和光伏電站均采用等值集中模型，即風(fēng)電場等效額定出力為所有風(fēng)機出力總和；光伏電站額定出力為所有光伏電池出力總和。

考慮到相鄰地區(qū)的風(fēng)電和光伏出力存在一定的負相關(guān)特性，本文選取Frank Copula函數(shù)作為風(fēng)-光聯(lián)合出力概率分布的連接函數(shù)。Frank Copula函數(shù)的密度函數(shù)可表示為［13］：

式中θ為隨機變量u、v的相關(guān)參數(shù)且θ≠0；當(dāng)θ＞0時表示 u、v正相關(guān)；θ→0時表示 u、v趨于獨立；θ＜0時表示u、v負相關(guān)。

Kendall秩相關(guān)系數(shù)τ與Frank Copula函數(shù)相關(guān)參數(shù)θ的關(guān)系為：

由式（1）、式（12）可得風(fēng)電場和光伏電站有功出力的聯(lián)合概率密度函數(shù)為：

式中 F（pw）、f（pw）和 F（ppv）、f（ppv）分別為風(fēng)電場和光伏電站有功出力的分布函數(shù)和概率密度函數(shù)；相關(guān)參數(shù)θ可由式（13）求得。

在不同Kendall秩相關(guān)系數(shù)下，采用本文方法抽樣得到的100組風(fēng)電場和光伏電站出力的樣本數(shù)據(jù)如圖2所示。

圖2 不同秩相關(guān)系數(shù)下風(fēng)、光電場有功出力Fig.2 Active power outputs of wind and photovoltaic farmswith different rank correlation coefficients

5 算例

5.1 測試系統(tǒng)

本文以圖3所示改造后的IEEE-14節(jié)點測試系統(tǒng)為算例進行仿真分析。假設(shè)風(fēng)電場W接入到節(jié)點13，光伏電站PV接入到節(jié)點14。系統(tǒng)發(fā)電機總裝機容量為572.4 MW，新能源裝機容量為200 MW，占比34.9%。風(fēng)機裝機容量100 MW，風(fēng)速服從尺度參數(shù)為14.117 8、形狀參數(shù)為2.017 8的 Weibull分布，且風(fēng)機的切入、額定、切出風(fēng)速分別為3 m／s、16 m／s和25 m／s。光伏發(fā)電裝機容量為100 MW，有功出力服從形狀參數(shù)為2.06和2.50的Beta分布。假設(shè)風(fēng)電場及光伏電站均采用功率因數(shù)為1的恒功率因數(shù)控制方式，所有負荷服從期望為穩(wěn)態(tài)值、標(biāo)準(zhǔn)差為期望值15%的正態(tài)分布。

5.2 算法驗證

采用本文概率潮流計算方法對圖3所示系統(tǒng)進行概率潮流分析，并與基于切片采樣的MCMC法得到的結(jié)果進行比較，驗證本文所提方法的準(zhǔn)確性和有效性。其中CMCMCS-CI的采樣規(guī)模為1 000次；切片采樣規(guī)模分別為105次和103次，認(rèn)為采樣規(guī)模為105次時計算所得結(jié)果為準(zhǔn)確值。

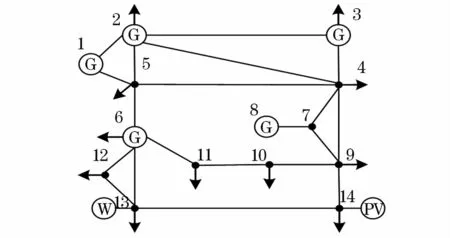
圖3 IEEE-14節(jié)點算例接線Fig.3 Diagram for IEEE 14-bus system

兩種方法所得節(jié)點14電壓幅值的期望μv、標(biāo)準(zhǔn)差σv，線路6-11有功功率期望μa、標(biāo)準(zhǔn)差σa，系統(tǒng)網(wǎng)損率期望μI、標(biāo)準(zhǔn)差σI如表1所示。

表1 IEEE-14節(jié)點系統(tǒng)概率潮流計算結(jié)果Tab.1 Probabilistic power flow results for IEEE 14-bus system

可見，采樣規(guī)模為103時，本文方法即可獲得較為準(zhǔn)確的結(jié)果，耗時304.67 s。而為得到準(zhǔn)確的結(jié)果，切片法需用時1 861.1 s。充分體現(xiàn)了改進的有效性和高效性。

5.3 風(fēng)電和光伏出力相關(guān)性對系統(tǒng)運行的影響

由于光伏電站晚上不出力而夜晚的風(fēng)速往往較大，因此地理上毗鄰的風(fēng)電場及光伏電站往往具有較強的負相關(guān)關(guān)系，但由于風(fēng)資源和光照等自然因素的隨機性，仍存在小部分時間呈現(xiàn)正相關(guān)性。而風(fēng)、光出力相關(guān)性會改變含風(fēng)-光發(fā)電系統(tǒng)出力的概率分布，進而影響電力系統(tǒng)潮流分布。目前，關(guān)于風(fēng)電光出力相關(guān)性對電力系統(tǒng)概率潮流影響的研究鮮有報道。本文將風(fēng)、光出力的Kendall秩相關(guān)系數(shù)τ分別設(shè)為 -0.9、-0.6、-0.3、τ→0、0.3、0.6和0.9，采用所提CMCMCS-CI概率潮流計算方法依次計算概率潮流，得到如下結(jié)果。

5.3.1 對節(jié)點電壓的影響

不同Kendall秩相關(guān)系數(shù)下，系統(tǒng)各節(jié)點電壓幅值和相角的期望值、標(biāo)準(zhǔn)差的變化曲線如圖4所示。風(fēng)、光的相關(guān)性對系統(tǒng)節(jié)點電壓幅值和相角的期望值影響較小，但對標(biāo)準(zhǔn)差影響較大，風(fēng)、光接入點最甚且標(biāo)準(zhǔn)差隨著τ的增大而增大。

不同Kendall秩相關(guān)系數(shù)下，節(jié)點14電壓幅值和相角的概率密度曲線和累積分布曲線分別如圖5所示。風(fēng)、光的相關(guān)性會影響系統(tǒng)節(jié)點電壓幅值和相角的概率分布，τ越大，風(fēng)、光出力變化的同步性越強，電壓幅值和相角的波動范圍越大，電壓越限的概率也越大。

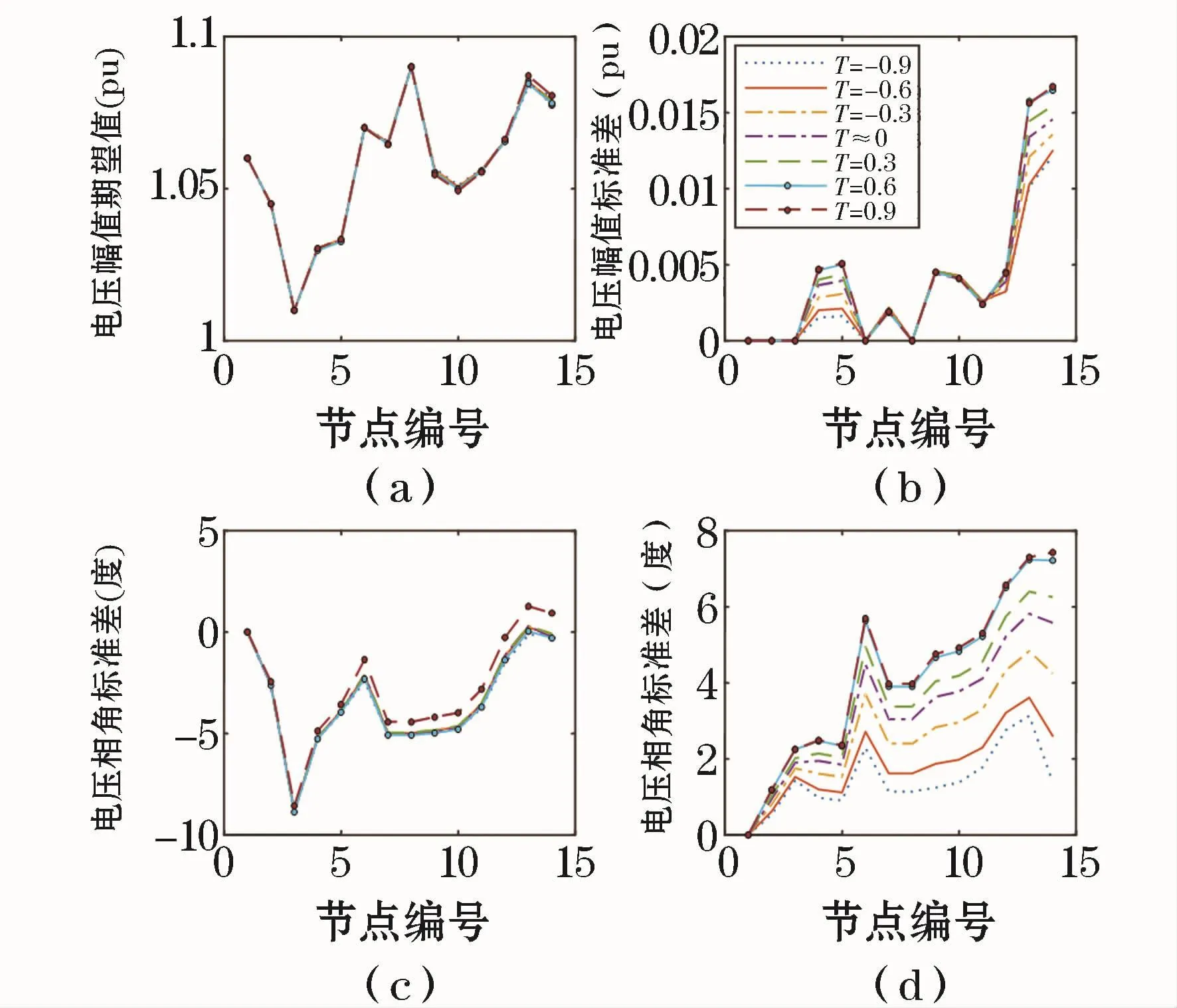
圖4 節(jié)點電壓幅值、相角的期望和標(biāo)準(zhǔn)差ig.4 Mean values and standard deviations of bus voltagemagnitudes and phase angle

圖5 節(jié)點14電壓幅值、相角的概率密度和累積分布曲線Fig.5 PDF and CDF of voltagemagnitude and phase angle at bus 14

5.3.2 對線路有功的影響

不同Kendall秩相關(guān)系數(shù)下，系統(tǒng)各線路傳輸有功的期望、標(biāo)準(zhǔn)差的變化曲線如圖6所示。線路有功的期望基本不受風(fēng)電和光伏出力相關(guān)性的影響，但其標(biāo)準(zhǔn)差受到較大的影響，風(fēng)、光電站之間的線路（線路13-14）有功功率標(biāo)準(zhǔn)差隨著τ的增加而減小，其它線路有功功率的標(biāo)準(zhǔn)差隨著τ的增大而增大。

不同Kendall秩相關(guān)系數(shù)下，線路6-11傳輸有功的概率密度曲線和累積分布曲線如圖7所示。風(fēng)、光的相關(guān)性同樣會影響線路傳輸有功的概率分布。隨著τ增大，風(fēng)、光出力變化的同步性增強，線路傳輸功率波動加劇，越限的概率也增加。

圖6 線路有功功率的期望和標(biāo)準(zhǔn)差Fig.6 Mean values and standard deviations of the active power in lines

圖7 線路6-11有功功率的概率密度曲線和累積分布曲線Fig.7 PDF and CDF of the active power in line 6-11

5.3.3 對網(wǎng)損率的影響

不同Kendall秩相關(guān)系數(shù)下，系統(tǒng)網(wǎng)損率的期望與標(biāo)準(zhǔn)差如表2所示。可見，τ增大時，系統(tǒng)網(wǎng)損率的期望μ和標(biāo)準(zhǔn)差σ都會增大。對期望的影響并不顯著，最大變化率為12.16%；對標(biāo)準(zhǔn)差影響較大，最大變化率達63.43%。

表2 網(wǎng)損率的期望值與標(biāo)準(zhǔn)差Tab.2 Mean and standard deviations of network loss rate

不同Kendall秩相關(guān)系數(shù)下，網(wǎng)損率的概率密度曲線和累積分布曲線如圖8所示，風(fēng)、光相關(guān)程度會影響系統(tǒng)網(wǎng)損率的概率分布。秩相關(guān)系數(shù)τ越大，系統(tǒng)網(wǎng)損率變小的概率越大，即風(fēng)、光互補有助于減小系統(tǒng)功率的損耗。因此，在電力系統(tǒng)分析中，如果低估或忽略風(fēng)電場和光伏電站出力的相關(guān)關(guān)系，將無法準(zhǔn)確得到系統(tǒng)網(wǎng)損率的概率分布。

圖8 系統(tǒng)網(wǎng)損率的概率密度曲線和累積分布曲線Fig.8 PDF and CDF of system network loss rate

6 結(jié)束語

本文提出一種基于Copula理論、切片采樣技術(shù)結(jié)合拉丁超立方抽樣的MCMC方法，應(yīng)用于高比例風(fēng)、光發(fā)電并網(wǎng)電力系統(tǒng)的概率潮流計算中。新方法能靈活處理輸入隨機變量的相關(guān)性，在保證精度的同時進一步提高了MCMC方法的計算效率。以改造后的IEEE-14節(jié)點系統(tǒng)為算例，驗證了方法的準(zhǔn)確性和有效性，并得到一些有實際意義的結(jié)論：

（1）風(fēng)電光伏間的相關(guān)關(guān)系會對概率潮流計算的輸出隨機變量（節(jié)點電壓、線路傳輸功率、網(wǎng)損率等）的期望值、標(biāo)準(zhǔn)差及概率分布產(chǎn)生一定影響，且對期望值的影響較小，對標(biāo)準(zhǔn)差及概率分布影響較大；

（2）隨著Kendall秩相關(guān)系數(shù)τ的增大，輸出隨機變量（節(jié)點電壓、線路傳輸功率、網(wǎng)損率等）的波動性隨之增強；

（3）考慮風(fēng)、光出力的相關(guān)性可以更準(zhǔn)確地評估風(fēng)、光并網(wǎng)對電力系統(tǒng)運行的影響，有助于風(fēng)電場和光伏電站的選址及電網(wǎng)規(guī)劃。