基于模糊聚類算法的油紙絕緣缺陷識別

王艷，徐祥海，侯偉宏，朱軍，高標，章潔菁

（國網浙江省電力公司杭州供電公司，杭州310016）

0 引 言

油浸紙絕緣結構是電力變壓器內絕緣系統的重要組成。該結構在變壓器中起支撐、絕緣和固定作用。在長期運行過程中受到電、熱、機械等多因素影響，導致絕緣性能下降。局部放電是油紙絕緣損傷的重要因素［1］。纖維紙因未充分浸漬形成氣穴、金屬導體突出部位電場強度增強或繞組連接處長時間過熱均會導致并加速局部放電發生。與IEC 60270［2］、GB／T 7345-2003［3］局部放電脈沖電流法相比，局部放電超高頻檢測具有檢測頻率高、信息量大、能夠有效避開低頻電磁干擾和適用于在線檢測等優點，它通過傳感電力設備內部局部放電所產生的超高頻電磁信號，實現抗干擾和局部放電的檢測與定位［4-7］。文獻［8］采用逐層最優小波去噪算法提取局部放電信號特征量，結果顯示去噪信號具有波形畸變率低和幅值誤差小的特點。通過小波包多尺度分析和網格維數提取變壓器典型放電模型產生局部放電超高頻信號特征量，并采用神經網絡對其進行識別［9-10］。

局部放電信號特征量能較好反映變壓器內部絕緣狀況。本文模擬變壓器內部絕緣缺陷，構造4種局部放電模型。采用對比不同小波層數和小波尺度尋求最優小波去噪效果。提取小波去噪前后局部放電超高頻信號特征量即小波能量和網格維數，組成綜合識別矩陣進行聚類及缺陷識別。采用模糊C-均值聚類算法對綜合向量進行聚類分析及識別。驗證了超高頻信號小波包多尺度能量參數和網格維數能有效表征四種局部放電模型特性以及模糊算法對油紙絕緣缺陷識別的適用性。為評估絕緣狀態、預測絕緣壽命打下堅實基礎。

1 油紙絕緣局部放電試驗

本文試驗回路根據標準GB 7354-2003，搭建在雙層屏蔽室內，局部放電超高頻測量系統及試驗接線示意圖，如圖1。其中：升壓變壓器由無暈試驗變壓器和自耦調壓器構成；保護電阻R起限流保護作用，阻值為7 kΩ，耐壓為50 kV；高壓耦合電容是1 000 pF，耐受電壓為60 kV；測量系統包括數字示波器（LeCory7200）、超高頻四階希爾伯特分形天線H［11］、電流傳感器 C、信號放大器、50Ω同軸電纜。脈沖電流傳感器通常在50 kHz至10 MHz頻帶內具有良好的測量線性度和幅頻特性。脈沖電流傳感器測量信號和希爾伯特分形天線分別經長5 m的同軸電纜連接示波器。試驗同時接收兩種傳感器C和H的信號。由于示波器的高通截止頻帶為1 GHz，因此試驗采樣率選為1 GHz。示波器的采樣率設置為1 GS／s，模擬帶寬為 1 GHz。

變壓器內部主要局部放電類型：油間隙放電；沿面放電；懸浮電位放電；油中氣泡放電；固體絕緣中的空氣間隙放電。本文針對變壓器絕緣內部放電形式和特點，利用變壓器專用纖維絕緣紙板和ABB礦物油構建局部放電試驗模型。構建4種油紙絕緣典型放電模型模擬典型絕緣缺陷：油中氣隙放電、電暈放電、楔形油隙放電和沿面放電。據標準CIGRE II采用黃銅電極和油紙絕緣模型搭建試驗模型系統，電極及各放電模型尺寸見圖2。氣隙放電模型在絕緣紙板預處理后制作。氣隙放電模型由上下兩層Φ 75 mm實心紙板和中間一層外徑Φ75 mm、內徑Φ 60 mm的環形紙板共同構成，為防止礦物油滲入氣隙模型，用環氧樹脂膠對其結合處進行密封后并用夾板加緊至模型投入使用。為防止電極接引線和高壓引線處發生電暈放電，高壓引線采用直徑為Φ10 mm的鋁管，電極螺帽為專門設計加工的球形螺帽；電極表面和邊緣均經過特殊處理盡可能消除電極表面尖角或毛刺的影響；局部放電試驗前先將一次篩選后的試樣在真空箱中經過90℃、2 h干燥處理，并對試樣進行室溫48 h真空充分浸油、祛氣以降低微水含量和氣泡對絕緣耐壓強度的影響；浸油后試樣的微水含量均值為0.8%，確保真實放電類型與放電模型一致。預處理后試樣進行二次篩選確保局部放電試驗四組共40個試樣形狀尺寸相同、紙板無損傷無異物。

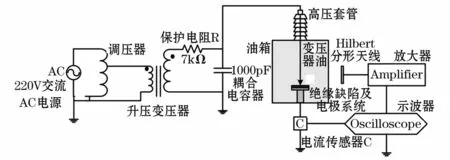
圖1 局部放電試驗系統Fig.1 PD experiment system

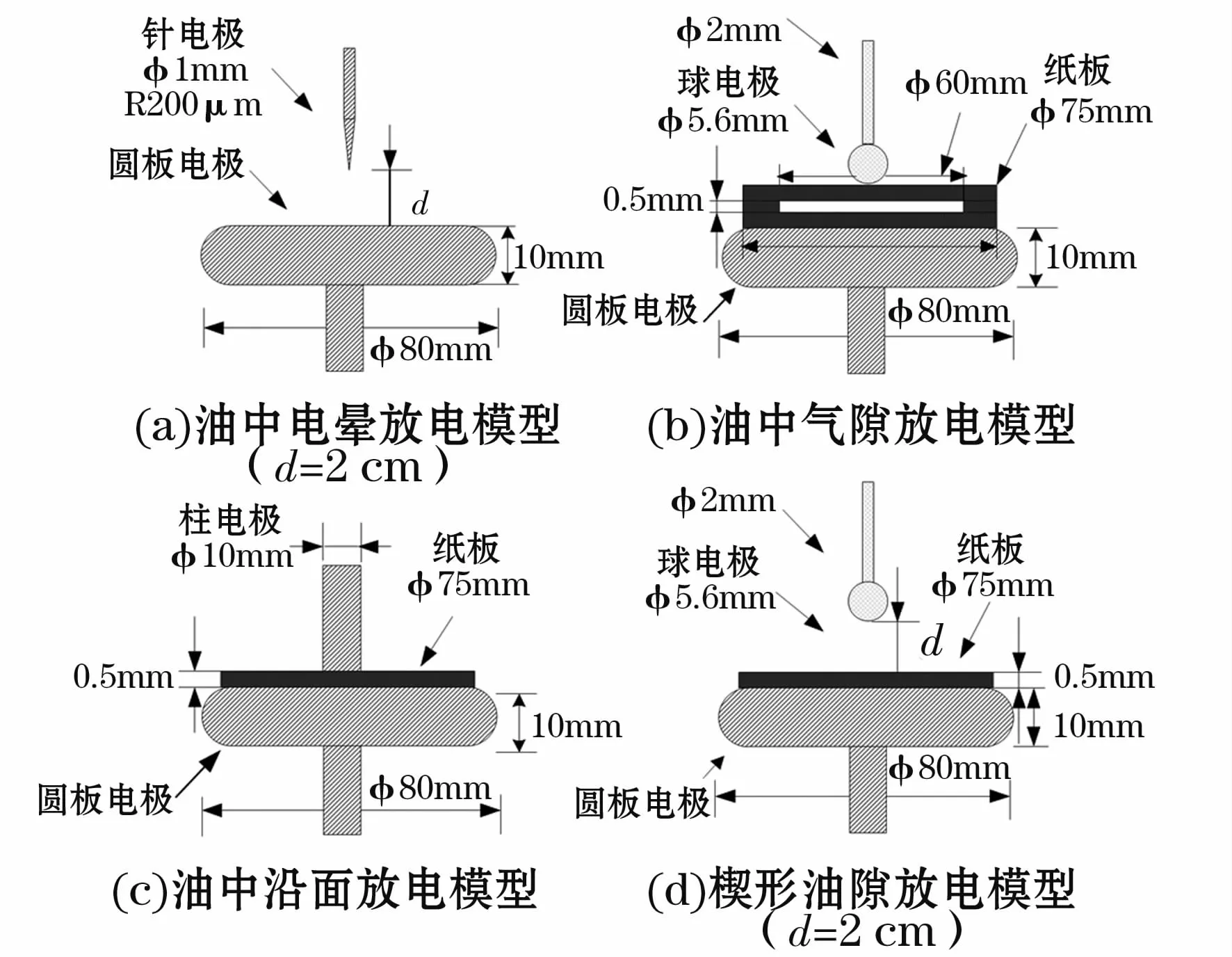
圖2 4種局部放電模型Fig.2 4 kinds of PD models

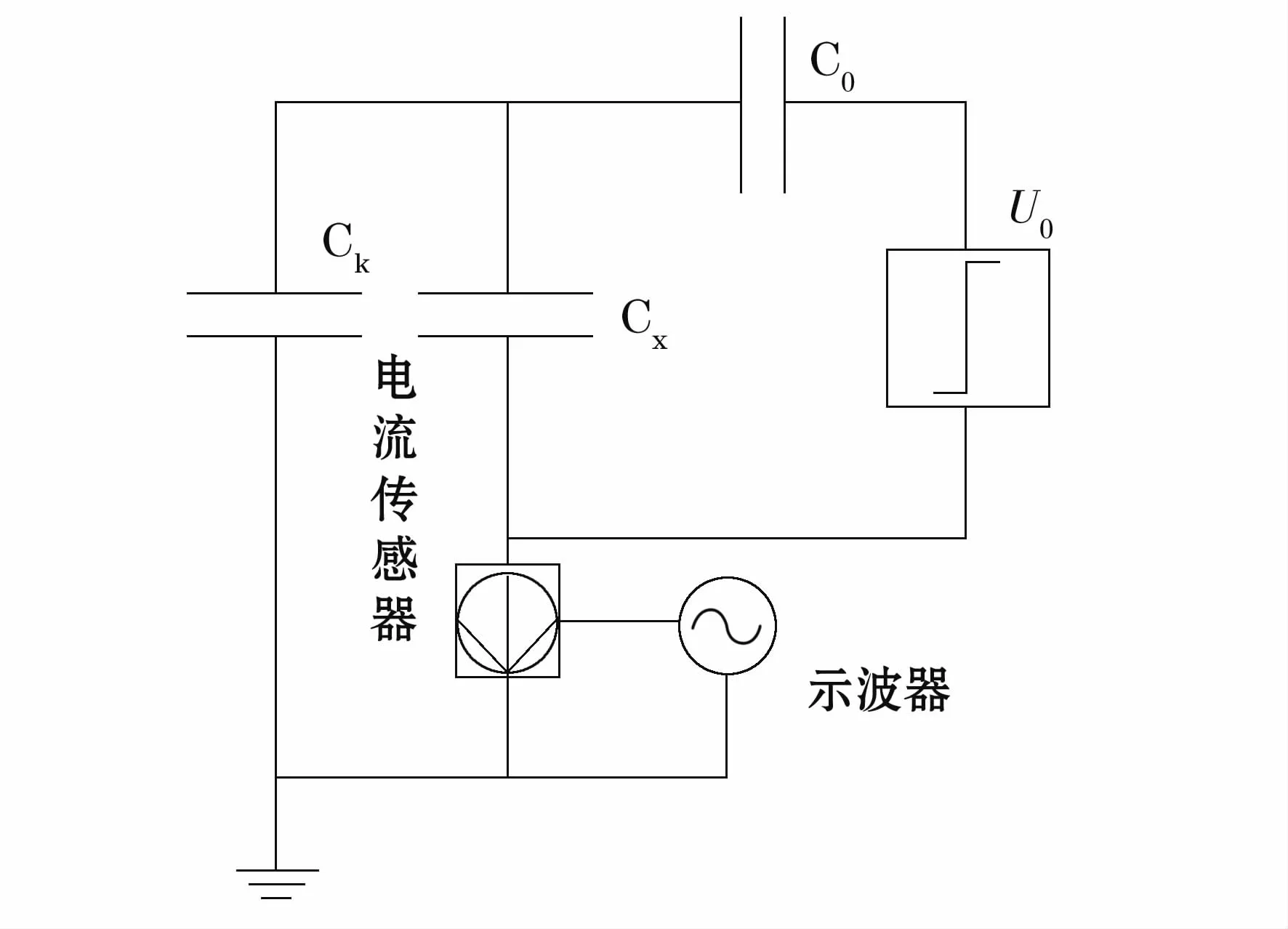
圖3 標定電路Fig.3 Calibration circuit

試驗采用逐步升壓法加速局部放電過程。試驗電壓采用樣品1.2倍的起始放電電壓，采樣電壓采用穩定放電時的試驗電壓。采樣電壓和采樣時間均因模型而異；試樣均在工頻條件下存儲局部放電三個電壓等級下150個單次放電波形。試驗中需調節調幅電路的放電倍數，因此在每組試驗結束后需按圖3所示接線校正試驗回路標定單位幅值的放電量，q0＝U0×C0其中U0是標定方波，C0是分度電容。

2 數據分析及處理

2.1 小波去噪

由于局部放電超高頻信號是一種奇異性較強的非平穩信號。采用小波變換提取白噪聲中局部放電脈沖信號比其它數字化濾波方法效果更好。為尋求最佳去噪結果，結合小波去噪僅去除白噪聲不影響幅值的特點，本文采用波形相似系數（NCC）［12-13］描述去噪前后波形間差別以確定最優小波層數和小波尺度。其定義為：

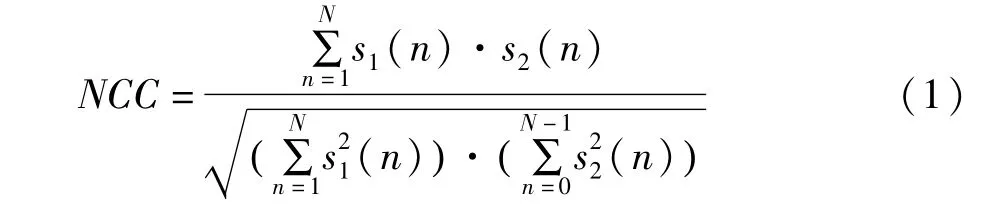
式中s1為原始放電波形；s2為小波去噪后放電波形。波形相似系數的取值范圍為［-1，1］，-1表示兩放電波形反向；0表示兩放電波形正交；1則表示兩放電完全相同［11］。

通過大量計算并統計NCC值選取各放電模型去噪小波層數和小波尺度最優值（選取范圍dept＝3～9，db＝1～10）。因數據量大本文僅列出11 kV下油中電暈放電一個單次波形的NCC值和三個電壓等級下4種放電模型的小波去噪參數最優選取值，詳見表1、表2所示。

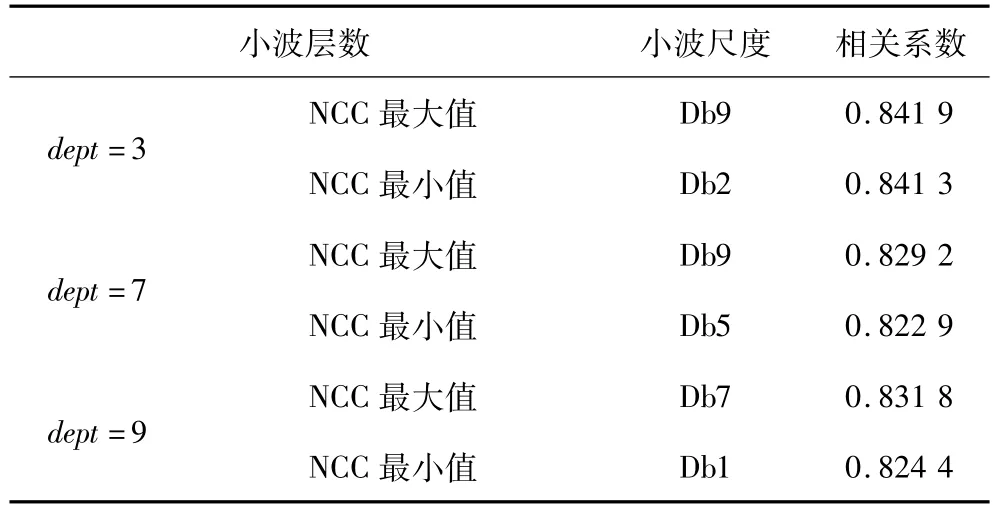
表1 11 kV下油中電暈放電一個單次放電波形的NCC值Tab.1 NCC of a single PD waveform for oil corona discharge under 11 kV

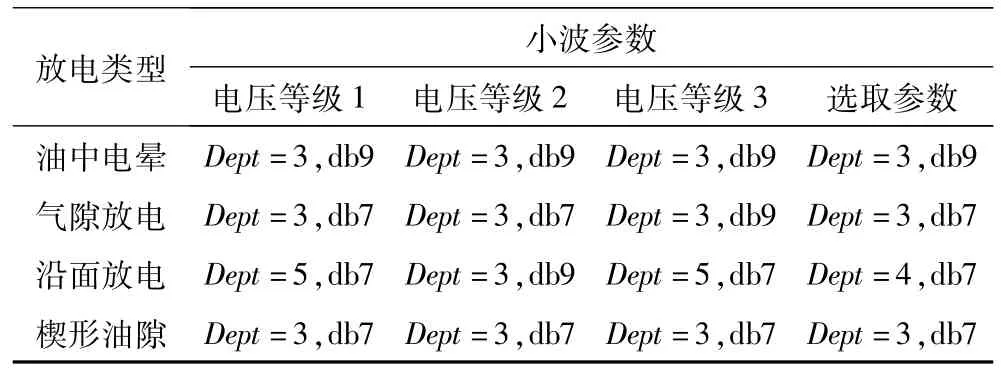
表2 各電壓等級下四種放電模型的最優小波去噪參數Tab.2 The optimum wavelet de-noising parameters of 4 kinds of PD models under different voltage levels

2.2 超高頻信號特征量提取

本文通過對小波去噪前后局部放電超高頻信號分別進行小波包多尺度變換，提取多尺度小波系數的網格維數和能量參數組成兩個綜合特征矩陣，反映各放電模型局部放電特征［13-14］。據表2參數對局放超高頻信號去噪后，將去噪前后局部放電超高頻信號分別進行多尺度小波包分解，采用改進差盒計數法［10］計算多尺度分解系數的網格維數。計算方法如下：

對二維分形曲線y＝f（x），用尺度為r的網格覆蓋分形曲線，所需網格數為Nr需滿足：

式中D為網格維數即分形曲線的分維數。改進DBC用一個網格狀柵格來覆蓋分形曲線，柵格的尺度定義為r。若第i個柵格內曲線段最小值與最大值分別為 fmin（i）和 fmax（i），覆蓋該曲線段的網格數 Nr可得。

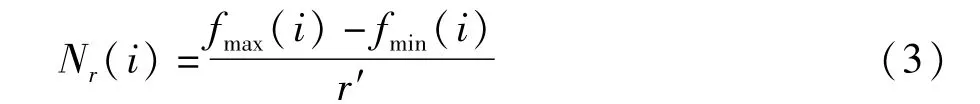
式中r′＝r／L；L為曲線的采樣點個數。則覆蓋全部分形曲線的網格數為：

計算出對應于不同尺度r的Nr，求出log（Nr）-log（r）擬合直線的斜率，其負數為分形曲線 y＝f（x）的網格維數。本文分形曲線為多尺度小波系數與小波系數個數的關系曲線。

其次，計算多尺度能量系數。方法如下：

假設被測信號 s＝｛si：i＝1，2，…，n｝經小波包分解后的全部系數為 c＝｛ci：i＝1，2，…，n｝，其總能量為：

任意分解空間的系數 ak＝｛akj：j＝1，2，…，n1｝的能量為：

則該分解空間的多尺度能量參數定義為：

信號N層小波包分解后的多尺度能量參數的向量為 E＝｛Ek：k＝1，2，…，2N｝且多尺度能量參數向量中各參數已歸一化；多尺度網格維數的向量為D＝｛Dk：k＝1，2，…，2N｝。二維曲線的網格維數在 （1，2）之間。則對多尺度網格維數向量中參數進行歸一化計算即求實際網格維數與1間差值。多尺度能量參數向量與網格維數向量構成局部放電超高頻信號的歸一化特征向量。參考小波去噪時小波尺度和小波層數的選取原則，經統計選取Dept＝4，db8時聚類效果和模型識別最優。表3為四層小波包分解多尺度特征參量與對應頻帶。

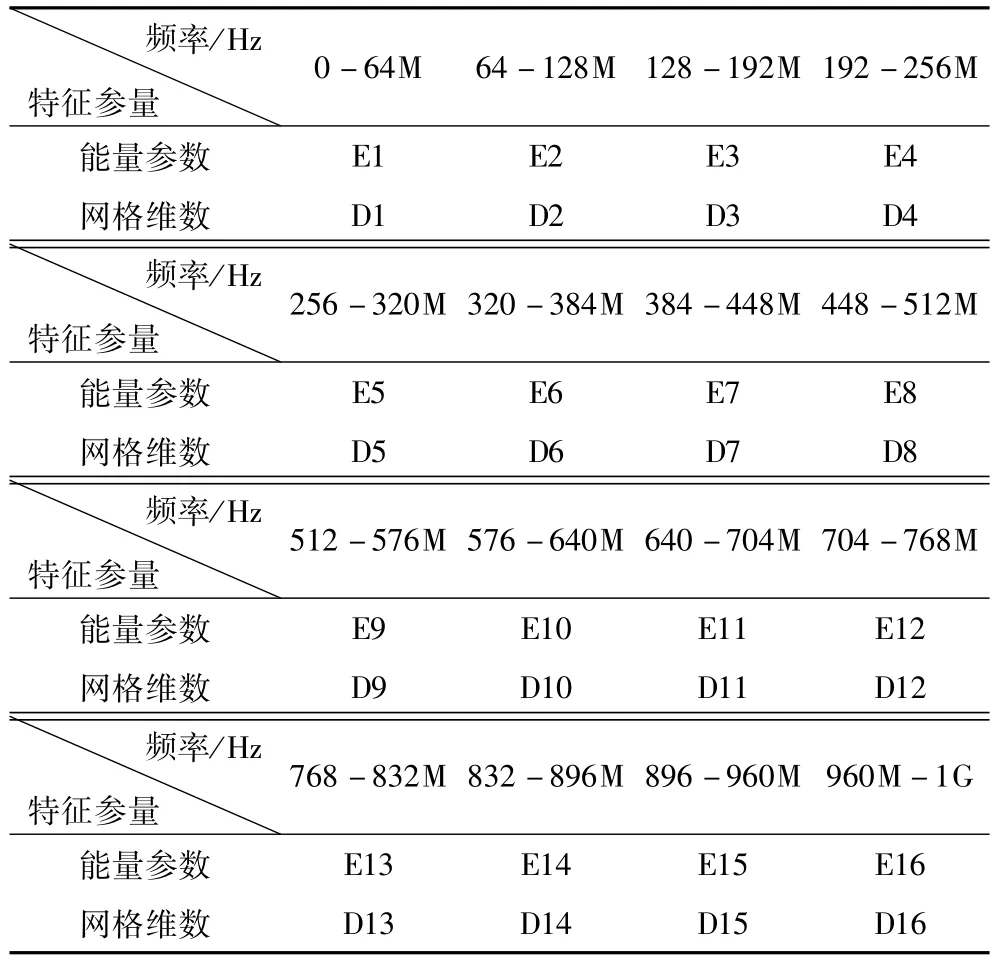
表3 局部放電超高頻信號四層小波包分解多尺度特征參量Tab.3 Multi-scale characteristic parameters of PD UHF signals using 4-layer wavelet packet decomposition

3 模糊C-均值聚類算法

為驗證超高頻特征參量能有效表征油紙絕緣4種放電類型，本文采用模糊C-均值聚類算法（Fuzzy C-Means algorithm，簡稱為 FCM）［15-17］，分別對局部放電樣本數據的32個特征量進行聚類分析及識別。

模糊C-均值聚類算法建立起樣本對類別的不確定性的描述。FCM算法的c個模糊組由n個數據的向量集 X＝｛x1，x2，…，xn｝組成，在非相似性指標的價值函數最小的前提下，計算每組的聚類中心。FCM聚類算法的目標函數為：

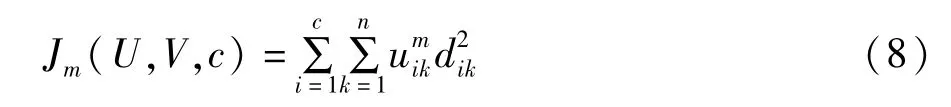
式中 V＝｛v1，v2，…，vc｝是聚類中心向量；U＝［uik］c＜n是隸屬度矩陣。對于任意 k（1≤k≤n），隸屬度矩陣需滿足以下條件：

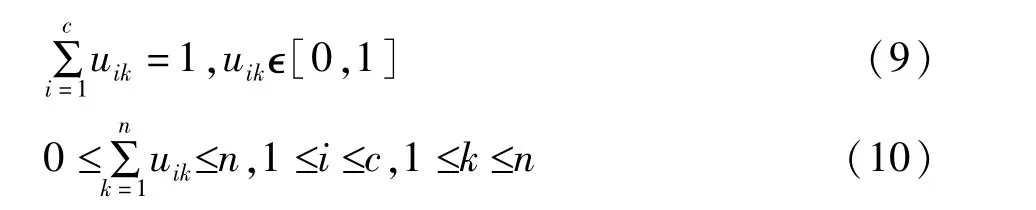
式（8）中，uik為 xk屬于第 i類的隸屬度；dik＝‖xk-vi‖2是樣本第i類中心向量vi與xk的歐幾里德距離；m是模糊度權重，取值區間為［1，∞），它影響模糊隸屬度矩陣的模糊度。FCM聚類算法步驟如下：

（1）選定需聚類個數 c（2≤c＜n），模糊度權重m，最大迭代次數 tmax和容許誤差 ε（0＜ε＜1），隨機產生初始化模糊隸屬度矩陣 U（0）＝［uik］c＜n；

（2）按照公式（11）計算 V（k）；

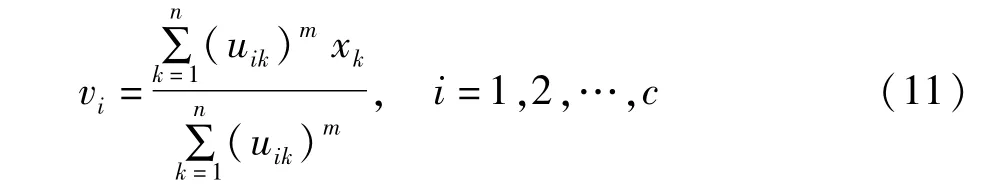
（3）按照式（12）修正模糊隸屬度矩陣即計算 U（k+1）；

（4）若滿足聚類終止條件‖U（k+1）-U（k）‖ ＜ε或迭代次數等于tmax，迭代計算結束，顯示識別結果和識別時間。否則，令k＝k+1，返回至第2步重復進行計算。

FCM算法通過迭代計算來修正聚類中心，使得誤差平方和目標函數最小。FCM算法采用拉格朗日乘數法，不依靠初始的聚類中心，是動態聚類算法。

4 識別結果分析

本文采用FCM算法對表征典型油紙絕緣缺陷的4種局部放電模型試樣超高頻樣本特征參量進行聚類和識別。特征參量矩陣由超高頻信號16個能量參數和16個網格維數組成。為驗證初始聚類中心對結果無影響，每次隨機選取聚類中心并連續進行聚類30次的條件下，比較FCM算法對4種放電模型超高頻特征參量的識別效果。參考文獻［12］FCM參數選取m＝2并在同參數下運行30次并獲取識別率。

由表4可知，對去噪前4種放電信號特征參量的識別平均值均高于65%，證明本文所采用的算法適用于該數據類型且FCM算法能正確識別4種局部放電類型；對比表4、表5去噪前后識別效果，識別率存在微小波動，各放電模型的識別率平均值均遠高于去噪前，充分表明小波去噪能夠有效提高正確識別率；小波包多尺度超高頻網格維數和能量參數能夠有效表征4種放電模型特性。

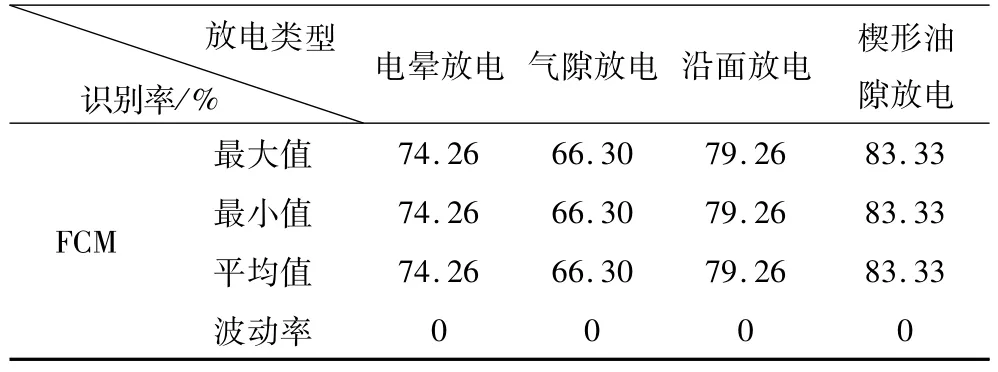
表4 去噪前信號特征參量識別率Tab.4 Recognition ratios of characteristic vectors before de-noising signals

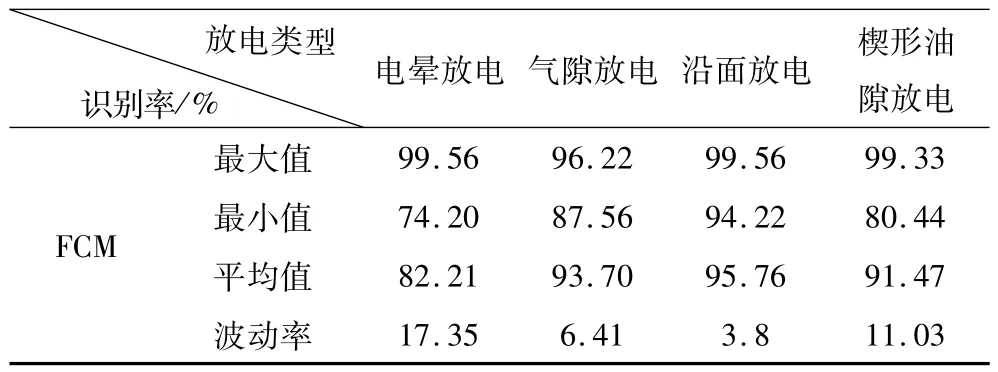
表5 去噪后信號特征參量識別率比較Tab.5 Recognition ratios comparison of characteristic vectors after de-noising signals

對比分析表5、表6可知，小波去噪后FCM算法的特性指標：正確識別率、最小識別率、識別穩定性和收斂性均明顯高于去噪前算法識別結果。小波去噪有效提高了FCM算法的識別率和識別穩定性。結合模糊聚類不需要訓練樣本和直接通過學習實現自動分類的特點綜合進行分析，小波去噪優化了FCM算法的對超高頻信號的識別和在線應用。

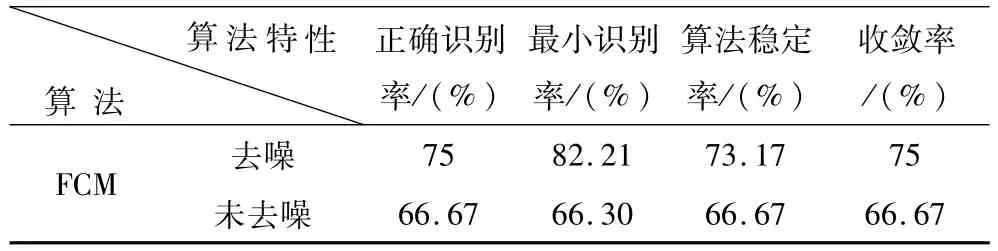
表6 去噪前后算法特性指標Tab.6 Characteristic indexes of both algorithms with and without de-noising

5 結束語

為有效識別電力變壓器油紙絕緣缺陷、評估絕緣狀態，結合局部放電信號能較好反映變壓器內部絕緣狀況的特點。本文通過引入小波算法對局部放電超高頻信號進行去噪的方法，研究FCM算法診斷油紙絕緣缺陷方法的適用性，得出以下結論：

（1）針對變壓器絕緣內部放電形式和特點，有效模擬變壓器油紙絕緣缺陷，確保試驗與放電模型的一致性，搭建4種典型油紙絕緣局部放電模型，并提取局放超高頻樣本數據；

（2）選取最優小波參量對超高頻信號進行去噪，分別提取去噪前后信號小波包多尺度16個能量參數和16個網格維數組成的兩個綜合識別矩陣；對比去噪前后識別結果表明，小波去噪能夠有效提高模糊聚類算法的正確識別率、最小識別率、識別穩定性、算法穩定性和收斂性；驗證了超高頻信號小波包多尺度能量參數和網格維數能有效表征四種局部放電模型特性；

（3）FCM算法通過迭代計算修正聚類中心，使誤差平方和目標函數達到最小。對比四種局部放電模型去噪前后特征參量識別結果。結果表明，模糊C-均值聚類算法能對局部放電超高頻未去噪信號進行有效分類，驗證了模糊算法對油紙絕緣缺陷識別的適用性。為局部放電超高頻信號特征參量有效應用于油紙絕緣系統狀態診斷提供依據，并為拓展變壓器壽命預測和狀態評估理論奠定基礎。