似曾相見曾相識(shí)，看似平淡需真功
——2017年全國(guó)卷解析幾何試題賞析

安徽 朱啟州

似曾相見曾相識(shí)，看似平淡需真功
——2017年全國(guó)卷解析幾何試題賞析

安徽 朱啟州

2017年全國(guó)卷解析幾何命題，以運(yùn)算求解能力為基礎(chǔ)，思維能力為核心，問(wèn)題設(shè)置側(cè)重體現(xiàn)對(duì)知識(shí)的理解和應(yīng)用，對(duì)考生邏輯思維的廣度和深度、運(yùn)算求解能力等有較高要求.整體上試題特點(diǎn)可用“似曾相見曾相識(shí)，看似平淡需真功”來(lái)概括.

一、合情推理總相宜

( )

綜上所述m∈(0,1]∪[9,+∞)，故選A.

【點(diǎn)撥】對(duì)于C上存在點(diǎn)M滿足∠AMB=120°，若用設(shè)而不求法，進(jìn)而轉(zhuǎn)化為任意性、存在性問(wèn)題來(lái)解決，就費(fèi)時(shí)費(fèi)力.特殊化、極端化等方法是解決選擇題常用方法.對(duì)本題來(lái)說(shuō)M位于短軸端點(diǎn)時(shí)，∠AMB最大；越近于長(zhǎng)軸端點(diǎn)，∠AMB越小，于是有橢圓C上存在點(diǎn)M滿足∠AMB=120°，只要∠AMB≥120°即可.這種解決問(wèn)題的方法主要運(yùn)用合情推理,在平時(shí)數(shù)學(xué)問(wèn)題解決中，我們往往自動(dòng)化式應(yīng)用這種思維方式，而不是有意識(shí)地使用罷了.因此，合情推理是發(fā)現(xiàn)與探尋解決數(shù)學(xué)問(wèn)題時(shí)首要的思考方式，具有普遍適用性.

二、看似容易需真功

面對(duì)選擇題，一般我們先通過(guò)對(duì)比篩選，在其中的兩個(gè)答案中選出正確答案而今年命題人不愿給我們這個(gè)機(jī)會(huì)，非要考考你的真本事.

【例2】(2017·全國(guó)卷Ⅰ理·10)已知F為拋物線C：y2=4x的焦點(diǎn)，過(guò)F作兩條互相垂直的直線l1，l2，直線l1與C交于A，B兩點(diǎn)，直線l2與C交于D，E兩點(diǎn)，則|AB|+|DE|的最小值為

( )

A．16 B．14

C．12 D．10

當(dāng)且僅當(dāng)k=±1時(shí)等號(hào)成立，|AB|+|CD|的最小值為16，故選A.

由解法一，知k2x2-2k2x-4x+k2=0,

≥4×(2+2)=16.

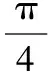
作準(zhǔn)線的垂線段AM，作x軸的垂線段AH，由拋物線的幾何性質(zhì)，

得|AF|=|AM|=|NH|=|NF|+|FH|=2+|AF|cosθ,

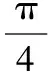
【評(píng)析】拋物線的焦半徑、焦點(diǎn)弦問(wèn)題，通常利用拋物線定義轉(zhuǎn)化為點(diǎn)到準(zhǔn)線的距離解決較方便；也可看作交點(diǎn)弦問(wèn)題，通過(guò)直線方程與圓錐曲線方程聯(lián)立，利用韋達(dá)定理求弦長(zhǎng)，這也是通法.而最值問(wèn)題通常要用函數(shù)方法或基本不等式來(lái)解決,都是通性通法.

三、縝思細(xì)算，顯智慧

2017全國(guó)卷數(shù)學(xué)解析幾何問(wèn)題，看似起點(diǎn)不高，似曾相識(shí)，但完整解決問(wèn)題并不容易.整體上看，與往年相比對(duì)學(xué)生運(yùn)算求解能力、思維能力要求明顯提高了.

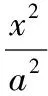
(Ⅰ)求C的方程；

(Ⅱ)設(shè)直線l不經(jīng)過(guò)P2點(diǎn)且與C相交于A，B兩點(diǎn).若直線P2A與直線P2B的斜率的和為-1，證明：l過(guò)定點(diǎn).

(Ⅱ)分析發(fā)現(xiàn)問(wèn)題應(yīng)是直線與圓錐曲線關(guān)系問(wèn)題，通常我們?cè)O(shè)l的方程，然后與曲線方程聯(lián)立，再應(yīng)用韋達(dá)定理解決.當(dāng)涉及直線斜率時(shí)，要注意考慮斜率是否存在.于是我們分兩種情況討論.

當(dāng)l的斜率存在時(shí)，設(shè)直線l的方程為y=kx+n(n≠1),A(x1,y1),B(x2,y2)，

得(1+4k2)x2+8knx+4n2-4=0,

又因?yàn)閚≠1,所以n=-2k-1,Δ=-64kgt;0,

只要klt;0即可.

于是直線l的方程為y=kx-2k-1,

即y=k(x-2)-1,

所以直線l過(guò)定點(diǎn)(2,-1).

安徽省淮北市杜集區(qū)教育局教研室)