商榷2017年高考題中表述欠嚴(yán)謹(jǐn)?shù)膸椎李}

北京 甘志國

商榷2017年高考題中表述欠嚴(yán)謹(jǐn)?shù)膸椎李}

北京 甘志國

一年一度的高考是考生、老師、家長、學(xué)校乃至全社會關(guān)注的重點話題．2017年的高考已塵埃落定，筆者作為一名高中數(shù)學(xué)老師，也抓緊時間認(rèn)真鉆研了本年度的高考數(shù)學(xué)真題(文理共計15套，其中上海、浙江文理同卷，江蘇文理除附加題外同卷)，發(fā)現(xiàn)了它們有試題常規(guī)、情景新穎、杜絕偏怪、難度在較大幅度的降低、文理相同題或姊妹題在增多等特點，這也與新課改的精神、教育乃培養(yǎng)人的活動、數(shù)學(xué)本來應(yīng)當(dāng)是人人能夠喜愛的美的科學(xué)合拍．

但筆者發(fā)現(xiàn)有少量高考題在表述上欠嚴(yán)謹(jǐn)：雖然原題不會太影響考生正確答題，但作為高考題的權(quán)威性及引用的廣泛性，還是要注意表述上的嚴(yán)謹(jǐn)．

筆者分別對2016、2015、2014年的高考題在表述上欠嚴(yán)謹(jǐn)之處也作了商榷.

(Ⅰ)求f(x)的導(dǎo)函數(shù)；

題2(2017·江蘇卷·20)已知函數(shù)f(x)=x3+ax2+bx+1(agt;0,b∈R)有極值，且導(dǎo)函數(shù)f′(x)的極值點是f(x)的零點.(極值點是指函數(shù)取極值時對應(yīng)的自變量的值)

(Ⅰ)求b關(guān)于a的函數(shù)關(guān)系式，并寫出定義域；

(Ⅱ)證明：b2gt;3a；

商榷普通高中課程標(biāo)準(zhǔn)實驗教科書《數(shù)學(xué)·選修2-2·A版》(人民教育出版社，2007年第2版)第9頁寫到：“當(dāng)x變化時，f′(x)便是x的一個函數(shù)，我們稱它為f(x)的導(dǎo)函數(shù)(derivative function)(簡稱導(dǎo)數(shù))”.既然教科書中已寫到“導(dǎo)函數(shù)簡稱導(dǎo)數(shù)”，數(shù)學(xué)表述應(yīng)以簡潔為標(biāo)準(zhǔn)，所以建議把題1中的“(Ⅰ)求f(x)的導(dǎo)函數(shù)”改為“(Ⅰ)求f(x)的導(dǎo)數(shù)”或“(Ⅰ)求f′(x)”；建議把題2中的“導(dǎo)函數(shù)f′(x)”改為“導(dǎo)數(shù)f′(x)”或“f′(x)”.

題3(1)(2017·天津卷文·2)設(shè)x∈R，則“2-x≥0”是“|x-1|≤1”的

( )

A.充分而不必要條件

B.必要而不充分條件

C.充要條件

D.既不充分也不必要條件

( )

A.充分而不必要條件

B.必要而不充分條件

C.充要條件

D.既不充分也不必要條件

(3)(2017·浙江卷·6)已知等差數(shù)列{an}的公差為d，前n項和為Sn，則“dgt;0”是“S4+S6gt;2S5”的

( )

A.充分不必要條件

B.必要不充分條件

C.充分必要條件

D.既不充分也不必要條件

(4)(2017·北京卷·理6，文7)設(shè)m，n為非零向量，則“存在負(fù)數(shù)λ，使得m=λn”是“m·nlt;0”的

( )

A.充分而不必要條件

B.必要而不充分條件

C.充分必要條件

D.既不充分也不必要條件

商榷普通高中課程標(biāo)準(zhǔn)實驗教科書《數(shù)學(xué)·選修2-1·A版》(人民教育出版社，2007年第2版)(下簡稱《選修2-1》)第11頁寫到：“……此時，我們說，p是q的充分必要條件，簡稱充要條件(sufficient and necessary condition)”.既然教科書中已寫到“充分必要條件簡稱充要條件”，數(shù)學(xué)表述應(yīng)以簡潔為標(biāo)準(zhǔn)，所以建議把本題第(3),(4)小題選項C中的“充分必要條件”均改為“充要條件”.建議把《選修2-1》第30頁第2(3)題末的“充分必要條件”也改為“充要條件”.

與《選修2-1》配套使用的《教師教學(xué)用書》(人民教育出版社，2007年第2版)第11頁給出的《選修2-1》第12頁第3題的答案是“(1)充分條件，或充分不必要條件；(2)充要條件；(3)既不是充分條件，也不是必要條件；(4)充分條件，或充分不必要條件.”所以建議把本題第(1),(2)，(4)小題選項A,B中的“而”字均去掉.

題4(2017·山東卷理·18)在心理學(xué)研究中，常采用對比試驗的方法評價不同心理暗示對人的影響，具體方法如下：將參加試驗的志愿者隨機分成兩組，一組接受甲種心理暗示，另一組接受乙種心理暗示，通過對比這兩組志愿者接受心理暗示后的結(jié)果來評價兩種心理暗示的作用，現(xiàn)有6名男志愿者A1，A2，A3，A4，A5，A6和4名女志愿者B1，B2，B3，B4，從中隨機抽取5人接受甲種心理暗示，另5人接受乙種心理暗示.

(Ⅰ)求接受甲種心理暗示的志愿者中包含A1但不包含B1的頻率.

(Ⅱ)用X表示接受乙種心理暗示的女志愿者人數(shù)，求X的分布列與數(shù)學(xué)期望EX.

商榷建議把題末的“EX”改為“E(X)”，這樣才與現(xiàn)行教材一致.

題5(2017·全國卷Ⅱ理·13)一批產(chǎn)品的二等品率為0.02，從這批產(chǎn)品中每次隨機取一件，有放回地抽取100次，X表示抽到的二等品件數(shù)，則DX=________．

解由題可得X～B(100，0.02)，所以DX=100×0.02×0.98=1.96.

商榷建議把題中的“DX”改為“D(X)”，這樣才與現(xiàn)行教材一致.

題6(2017·上海卷·15)已知a，b，c為實常數(shù)，數(shù)列{xn}的通項xn=an2+bn+c，n∈N*，則“存在k∈N*，使得x100+k,x200+k,x300+k成等差數(shù)列”的一個必要條件是

( )

A.a≥0 B.b≤0

C.c=0 D.a-2b+c=0

商榷建議把題中的“通項”改為“通項公式”，這樣才與現(xiàn)行教材一致.

普通高中課程標(biāo)準(zhǔn)實驗教科書《數(shù)學(xué)5·必修·A版》(人民教育出版社，2007年第3版)第29頁寫到“如果數(shù)列{an}的第n項與序號n之間的關(guān)系可以用一個式子來表示，那么這個公式叫做這個數(shù)列的通項公式.”

題7(2017·全國卷Ⅰ文·17)記Sn為等比數(shù)列{an}的前n項和.已知S2=2，S3=-6.

(Ⅰ)求{an}的通項公式；

(Ⅱ)求Sn，并判斷Sn+1，Sn，Sn+2是否成等差數(shù)列.

商榷題末的句號應(yīng)改為問號.

題8(2017·全國卷Ⅰ理·19)為了監(jiān)控某種零件的一條生產(chǎn)線的生產(chǎn)過程，檢驗員每天從該生產(chǎn)線上隨機抽取16個零件，并測量其尺寸(單位：cm)．根據(jù)長期生產(chǎn)經(jīng)驗，可以認(rèn)為這條生產(chǎn)線正常狀態(tài)下生產(chǎn)的零件的尺寸服從正態(tài)分布N(μ,σ2)．

(Ⅰ)假設(shè)生產(chǎn)狀態(tài)正常，記X表示一天內(nèi)抽取的16個零件中其尺寸在(μ-3σ,μ+3σ)之外的零件數(shù)，求P(X≥1)及X的數(shù)學(xué)期望；

(Ⅱ)一天內(nèi)抽檢零件中，如果出現(xiàn)了尺寸在(μ-3σ,μ+3σ)之外的零件，就認(rèn)為這條生產(chǎn)線在這一天的生產(chǎn)過程可能出現(xiàn)了異常情況，需對當(dāng)天的生產(chǎn)過程進行檢查．

(ⅰ)試說明上述監(jiān)控生產(chǎn)過程方法的合理性；

(ⅱ)下面是檢驗員在一天內(nèi)抽取的16個零件的尺寸：

9．9510．129．969．9610．019．929．9810．0410．269．9110．1310．029．2210．0410．059．95

附：若隨機變量Z服從正態(tài)分布N(μ,σ2)，則P(μ-3σlt;Zlt;μ+3σ)=0.997 4.

商榷普通高中課程標(biāo)準(zhǔn)實驗教科書《數(shù)學(xué)·選修2-3·A版》(人民教育出版社2009年第3版，2015年第2次印刷)第73頁給出的數(shù)據(jù)是

P(μ-σ≤X≤μ+σ)=0.682 6

P(μ-2σ≤X≤μ+2σ)=0.954 4

P(μ-3σ≤X≤μ+3σ)=0.997 4

而該書“2016年第3次印刷”時給出的數(shù)據(jù)是

P(μ-σ≤X≤μ+σ)=0.682 7

P(μ-2σ≤X≤μ+2σ)=0.954 5

P(μ-3σ≤X≤μ+3σ)=0.997 3

這次高考題中給出的數(shù)據(jù)又是“P(μ-3σ≤X≤μ+3σ)=0.997 4”.建議給出權(quán)威、統(tǒng)一的數(shù)據(jù).

題9(2017·北京卷文·15)已知等差數(shù)列{an}和等比數(shù)列{bn}滿足a1=b1=1,a2+a4=10,b2b4=a5．

(Ⅰ)求{an}的通項公式；

(Ⅱ)求和：b1+b3+b5+…+b2n-1．

解(Ⅰ)(過程略)an=2n-1.

(Ⅱ)設(shè)等比數(shù)列{bn}的公比為q，由題設(shè)可得

b2b4=b1q·b1q3=(q2)2=9，q2=±3.

①當(dāng)q2=3時，b2n-1=b1(q2)n-1=3n-1，

②當(dāng)q2=-3時，b2n-1=b1(q2)n-1=(-3)n-1，

評注該解法(在復(fù)數(shù)范圍內(nèi)求解)顯然不是出題者的初衷，但是目前的文科、理科高三學(xué)生都學(xué)習(xí)了復(fù)數(shù)，所以以上解法并無不妥.

解答題10時也會遇到這樣題9的情形.所以建議把題9及題10中的“等比數(shù)列”都改成“各項都是實數(shù)的等比數(shù)列”.

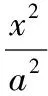
證明設(shè)P(x,y)(x≤-a)，

由x≤-a，可得|PF|的取值范圍是[c-a,+∞).

同理可證，|QF|的取值范圍是[c+a,+∞).

( )

A.1033B.1053C.1073D.1093

北京市豐臺二中)