解析幾何中的“多曲線問題”

安徽 羅春陽

解析幾何中的“多曲線問題”

安徽 羅春陽

解析幾何在高考中占有非常重要的位置，而對于圓錐曲線的考查則是解析幾何的核心問題、重點問題，也是難點問題.除小題外，圓錐曲線多處于次壓軸位置，綜合考查與圓錐曲線相關的幾何問題，主要可分為“單曲線問題”與“多曲線問題”，“單曲線問題”即只有一個圓錐曲線，綜合直線、三角形、四邊形等進行考查；而“多曲線問題”則是指問題中綜合了圓與圓錐曲線、圓錐曲線與圓錐曲線，再結合直線、三角形，四邊形等進行考查，幾何關系復雜程度高于“單曲線問題”.

一、直徑直線化

在圓與圓錐曲線問題中，常會有以橢圓上兩點連線的直線形成圓，可將直徑直線化，把問題化為直線與圓錐曲線相交，兩點滿足特定關系進行解題.

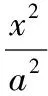
(Ⅰ)求橢圓E的離心率；

(Ⅱ)令橢圓E：x2+4y2=4b2，A(x1，y1)，B(x2，y2)，M(-2，1)為AB中點，

根據橢圓對稱性可知，AB⊥x軸時，不合題意，故舍去，

則可令直線AB為y=k(x+2)+1代入橢圓E的方程可得，

(1+4k2)x2+8k(2k+1)x+4(2k+1)2-4b2=0，

則x1x2=8-2b2，

解得b2=3，

【評析】本題問題主要集中在如何體現圓與橢圓交于直徑，而直徑的特征在于線段的長度與線段的中點.在解決過程中轉化成直線與橢圓交于兩點A，B，在令直線AB過程中要體現直線AB過圓心M(-2，1)這一條件.AB中點為M，且AB長度的直徑，通過聯立方程組利用韋達定理與弦長公式解決問題，當然作為中點弦問題，也可利用點差法.

(Ⅰ)求C1的方程；

(Ⅱ)橢圓C2過點P且與C1有相同的焦點，直線l過C2的右焦點且與C2交于A，B兩點.若以線段AB為直徑的圓過點P，求l的方程.

二、直線的側重對待與并列處理

問題中出現多條直線時，可通過直線與圓錐曲線相交，利用韋達定理為入手點，將個別直線作為重點直線處理，若多直線并列呈現多種形式，則處理方式相同.

【例3】(2017·合肥二模)如圖拋物線E：y2=2px(pgt;0)與圓O：x2+y2=8相交于A，B兩點，且點A橫坐標為2，過劣弧AB上動點P(x0，y0)作圓O的切線交拋物線E于C，D兩點，分別以C，D為切點作拋物線E的切線l1，l2，l1與l2交于M.

(Ⅰ)求p的值；

(Ⅱ)求動點M的軌跡方程.

【解析】(Ⅰ)p=1.

【評析】本題涉及直線、圓、拋物線的幾何位置關系，其中三條直線如何來處理是本題的關鍵，直線l與圓相切，與拋物線相交于C，D兩點，直接影響M的變化規律，故直線l是關鍵直線.直線l方程與拋物線方程聯立利用韋達定理，得出C，D點坐標關系，而C，D點的坐標關系則直接使得動點M的變化遵循一定的規律，進而得出M軌跡方程.另外P點在指定劣弧上運動，對最終的變化范圍給予了限制，為了更好地體現這一變化范圍，用P點坐標解出直線CD確為合理選擇.

【例4】(2012·湖南卷理·21)在直角坐標系xOy中，曲線C1上的點均在圓C2：(x-5)2+y2=9外，且對C1上任意一點M，M到直線x=-2的距離等于該點與圓C2上點的距離的最小值.

(Ⅰ)求曲線C1的方程；

(Ⅱ)設P(x0，y0)(y0≠±3)為圓C2外一點，過P作圓C2的兩條切線，分別與曲線C1相交于點A，B和C，D.證明：當P在直線x=-4上運動時，四點A，B，C，D的縱坐標之積為定值.

【解析】(Ⅰ)y2=20x.

(Ⅱ)令P(-4，y0)(y0≠±3)，則兩條切線斜率均存在，且不為零，

令過P點的圓C2：(x-5)2+y2=9的切線為

kx-y+y0+4k=0，

令兩切線PA，PB斜率分別為k1，k2，

令A(x1，y1)，B(x2，y2)，C(x3，y3)，D(x4，y4)，

得k1y-20y+20(y0+4k1)=0，

=6 400.

即為所求定值.

【評析】本題主要涉及兩個位置關系，直線與圓相切，直線與拋物線相交，因只有兩條直線，且并列存在，故思維線索比較明確，即先令好一條直線，直線與圓相切，得出一結論待應用，該直線與拋物線相交，形成交點，得到縱坐標乘積表達式，另外一條直線的情況，可類比直接寫出結論，簡化運算.再利用結論作為橋梁，可得四個點縱坐標乘積定值.

三、相切限制，相交解題

一條曲線的切線與另一條曲線相交，利用相切關系得到與直線相關的結論，利用相交關系聯立方程組結合相切關系，所得結論進行解題.

(Ⅰ)求橢圓的方程；

(Ⅱ)設P是E上的動點，且位于第一象限，E在點P處的切線l與C交于不同的兩點A，B，線段AB的中點為D.直線OD與過P且垂直于x軸的直線交于點M，求證：點M在定直線上.

【解析】(Ⅰ)x2+4y2=1.

令A(x1，y1)，B(x2，y2)，D(x0，y0)，

【評析】本題關鍵直線為過P點與拋物線相切的直線l，直線l與拋物線相切，與橢圓相交，或者說拋物線通過直線l對l與橢圓相交的相關幾何特征與規律產生影響，即通過P點令出切線，切線方程與橢圓聯立，形成方程組，利用韋達定理，得到坐標關系，再根據題意，利用坐標關系，將問題代數化，即可得到最終的幾何結論.

(Ⅰ)求橢圓的方程；

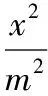
①若切線l垂直于x軸，則其方程為x=±2，

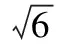
②若切線l不垂直于x軸，可設其方程為y=kx+b，

由Δ=0得b2=4k2+3.

令M(x1，y1)，N(x2，y2)，

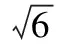
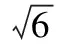
【評析】本題主要位置關系為“一切一交”，即直線l與一支橢圓相切，與另一支相交，最終立足點在于直線與橢圓相交，但直線l為另一橢圓切線，故直線的變化受到其影響，即小橢圓通過與直線l相切來影響和控制直線，而直線與大橢圓相交，完成了小橢圓通過切線作用于大橢圓進而影響其切線與大橢圓相交產生的弦長范圍.

安徽合肥肥西實驗高級中學)