合作學習與數學建模在常微分方程教學中的應用

苗春梅，張曉穎

(長春大學 理學院, 長春 130022)

合作學習與數學建模在常微分方程教學中的應用

苗春梅，張曉穎

(長春大學 理學院, 長春 130022)

常微分方程是高等院校數學類、信息與計算科學等專業的重要專業基礎課之一。如何使學生在學習過程中掌握常微分方程的思想方法、具備以常微分方程為理論工具解決實際問題的能力，是常微分方程教學與改革中必須要解決的問題。本文結合常微分方程課程的特質，探討合作學習模式與數學建模思想融入其教學過程的機理與方式，培養學生研究學習與創造學習的思維與能力。

常微分方程；合作學習；數學建模思想；教學改革

“高等教育面向21世紀教學內容和課程體系改革計劃”的目標是培養具有以創新精神和實踐能力為核心的綜合素質的高級人才。具有創新精神和實踐能力的人才必須掌握現代科學技術研究的方法和數學技術，而數學技術主要由數學分析技術、數學建模技術、數學軟件技術、數學實驗技術等組成[1]。

常微分方程源于對物體運動過程的數學研究，是一門應用性很強的學科，在物理、生物、機械工程等領域都有著廣泛的應用。比如，導彈彈道計算與飛機飛行中的穩定性研究，生物種群穩定性的研究等都歸為常微分方程模型[2]。就信息與計算科學專業而言，“常微分方程”是“數學分析”、“高等代數”和“解析幾何”的后繼課程，又是“數學建模”、“數值分析”等課程的先修課程，是從理論向應用過渡的紐帶課程。因此，如何在常微分方程課程的教學中突出其應用性與數學模型的思想，是其教學亟待解決的重要問題。長期以來，以理論推導與計算為主導的教學模式消解了常微分方程的實踐性，以至學生對其應用性缺乏認識。

基于此，本文提出“合作學習模式”與“數學建模思想”相結合的教學模式，引入開放性題，讓學生通過合作學習模式、應用數學建模思想解決問題，培養學生的創新能力、合作能力與研究能力。

1 合作學習與數學建模

1.1 合作學習模式

合作學習興起于20世紀70年代的美國，經過30多年的理論研究和實踐發展，合作學習已成為世界上許多國家普遍采用的教學理論與實踐策略，被認為是“當代教育理論、研究和實踐中影響最大和成果最多的領域之一”。

不同的學者對合作學習的有著各具特色的研究與推進。美國約翰霍布金斯大學的Slavin提出了“學生小組成就區分法”，“合作學習是指使學生在小組中從事學習活動，并依據他們整個小組的成績獲取獎勵或認可的課堂教學技術”[3]。美國明尼蘇達大學的約翰遜兄弟認為：“合作學習就是在教學中運用小組，使學生共同活動以最大程度地促進他們自己以及他人的學習。”[4]

20世紀80年代末、90年代初，我國學者開始關注合作學習的研究與應用。王坦認為：“合作學習是一種旨在促進學生在異質小組中互相合作，達到共同的學習目標，并以小組的總體成績為獎勵依據的教學策略體系。”[5]黃政杰認為：“合作學習是學生一起工作達成其共同的目標，此目標不但有利于己，也有利于其他人。合作學習采取小組學習方式，學生一起學習進而擴大自己和他人的學習。在合作學習中，所有成員式相互得力的，你的成功也就是我的成功，我的失敗也正是你的失敗，這是一種命運共同體的狀態，是屬于積極互賴的情景。”[6]

合作學習的課堂實施是合作學習理論在課堂教學中的應用與實踐，但是國內大部分的合作學習的課堂案例都是中小學課程教學，缺乏在大學課堂教學中的優秀案例。

1.2 合作學習與數學建模活動的關系

數學建模于20世紀六七十年代進入西方國家的大學，80年代初開始進入我國大學。數學建模活動是培養學生自學能力、合作能力、研究能力和創新能力的有效途徑，近年來受到數學教育者的廣泛關注。

合作學習，即“學生在小組中從事學習活動，并以他們小組的表現為依據獲得獎勵或認可的課堂教學技術”。在數學建模競賽活動中，合作學習主要體現在教師與學生的合作學習、學生與學生的合作學習兩個方面，即在教師的指導下，學生以小組為單位進行學習。因此，合作學習是數學建模活動重要的組織模式。

2 設置常微方程開放性題目

在常微分方程教材中，習題基本上是為了使學生理解和掌握數學結論而設計的。在這種情況下，學生在學習過程中往往容易產生以死記硬背代替主動參與、以機械方法代替智力活動的傾向。要改變這種情況，使學生的學習更多地體現以學生為主體的積極探究精神，適當增加開放題，讓學生以合作學習的方式，應用數學建模的思想解決問題是必要的。

2.1 開放題的設置原則

(1)問題導出理論、理論深化問題。常微分方程課程教學的開放題設置要與教材內容有機結合起來，而不是做成各自獨立的兩套系統。比如在講授一階和二階常微分方程內容時，設置相關的應用性開放題，使學生了解問題背景，能夠學以致用。另一方面，開放題的設置應與微分方程發展的主流相結合，使學生了解前沿問題的研究進展。這要求教師要對微分方程、動力系統和非線性科學領域的主流問題有所研究，從而滲透到起奠基性作用的常微分方程課程的教學中。

(2)針對實際能力、引導探索興趣。地方高等院校是一個基礎和能力有較大差異的學生群體，大約可以分成三類：A類，基礎和能力較強；B類，基礎和能力一般；C類，基礎和能力相對較弱。因此，常微分方程課程教學中開放題的設置，也要根據學生的能力和水平分層設置，不能“一刀切”。

2.2 開放題的解決方法

學生要以小組的形式進行合作學習，結合數學建模的思想，在老師的指導下解決問題。以下根據筆者的研究方向，選取常微分方程課程教學中的開放題，通過指導學生解決這兩類問題的過程，闡釋課程教學中開放題的解決方法。

(1)生物種群模型。生物種群模型的穩定性問題是筆者一直研究的課題，在常微分方程課程教學中引入相關的生物模型作為開放題，能夠使學生更好地掌握一階常微分方程理論、應用和前景。Logistic模型[7]

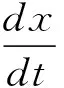
(2.1)

是一階非線性常微分方程，是生物學中最簡單的單種群模型，最早由比利時數學家Verhulst于1838年提出的描述種群增長過程的數學模型。1920年，美國人口學家Pearhe和Reed在研究美國人口問題時再次提出這個方程，稱之為Verhulst-pearl阻滯方程，后來被稱為Logistic模型。學生學習了一階常微分方程的基本理論之后能夠求解該方程。

首先，對學生進行分組。共7個人：3個A類學生，2個B類學生，2個C類學生。其次，提出問題，建立模型。由2個B類學生查閱資料，分析數據，建模。然后，解決問題。由2個C類學生根據所學的一階常微分方程理論求解。最后，分析問題。由3個A類學生做如下幾方面的工作：① 結合模型的建立和求解，分析問題，并提出修改和推廣建議。② 在老師的指導下，查閱該問題的研究進展和發展前景。③ 撰寫成文。

(2)振動問題。1831年，英國曼徹斯特的布勞頓橋上一隊士兵齊步通過的時候橋突然坍塌。1940年，美國華盛頓塔克馬大橋突然發生振動，振幅達到28英尺。振動是工程中常見現象，研究振動規律有著極其重要的意義。近些年，筆者關注經典的振動方程

mx″+kx′+hx=f(x).

(2.2)

的研究。根據我們的研究成果，在常微分方程課程教學中引入經典的振動方程(2.2)作為二階常微分方程理論的開放題，以使學生更好地掌握二階常微分方程理論、應用和前景。對學生進行分組解決開放問題(2.2)的過程和方法同問題(2.1).

3 結語

在常微分方程課程的教學中，通過設置諸如以上的應用性問題作為開放題目，組織學生分組合作進行研討，提出建模的基本思路，然后教師結合常微分方程的思想方法與學生進行深入研討，推進問題的解決。在這樣的學習過程中，一方面，教師能夠結合具體問題很好地具體向學生解釋常微分方程的基本理論，形成學生對常微分方程的系統認識與邏輯把握；另一方面，學生在互動中真正體會到合作的意義，在爭議與碰撞中表現了自己的創造性思考與團隊意識，形成了創新思考的內在動力和修正思想的自覺意識。同時，設置開放題應該注意以下兩個問題：一是避免流于形式，問題不要過大，要注重精細；二是教師要對開放題有一定的研究。

[1] 石永福，王立群. 現代數學技術及其影響 [J]. 西北師范大學學報(自然科學版)，2005(2)：94-97.

[2] JI.C.龐特里亞金.常微分方程 [M].林武忠，倪明康，譯.北京：高等教育出版社，2006.

[3] M.C. Wittrock. The cognitive movement in instruction [M]. Educational Psychology, 1978(71)：60-66.

[4] 大衛.W. 約翰遜，羅格.T. 約翰遜，卡爾. A.史密斯.合作學習的原理與技巧：在教與學中組建有效的團隊[M].劉春紅，譯.北京：機械工業出版社，2002.

[5] 王坦. 合作學習導論 [M]. 北京：教育科學出版社，1994.

[6] 黃政杰，林佩璇. 合作學習 [M].臺北：五南出版社，1996.

[7] 余愛華. Logistic模型的研究 [D]. 南京：南京林業大學，2003.

責任編輯：劉 琳

ApplicationofCooperativeLearningandMathematicalModelinginOrdinaryDifferentialEquationTeaching

MIAO Chunmei, ZHANG Xiaoying

(College of Science, Changchun University, Changchun 130022, China)

Ordinary differential equation is one of the important professional basic courses in mathematics as well as informational and calculative science in universities. It is a fundamental problem in teaching and reform to make students get the thinking methods of the ordinary differential equations and have the ability to solve practical problems by using ordinary differential equalities as theoretical tools. This paper, combining with the characteristics of ordinary differential equation course, discusses the mechanism and way of integrating the thought of cooperative learning and mathematical modeling into ordinary differential equation teaching, trying to cultivate the thinking and ability of students’ research learning and creative learning.

ordinary differential equation; cooperative learning; mathematical modeling thought; teaching reform

2017-04-06

吉林省教育科學規劃課題(GH170133)；吉林省高等教育學會2017年度高教科研課題(JGJX2017B28)

苗春梅(1977-)，女，遼寧大連人，副教授，博士，主要從事常微分方程理論研究。

G642

A

1009-3907(2017)10-0088-03