趙森烽-克勤概率的賭本分配研究與期望值定理
趙克勤,趙森烽
(1.諸暨市聯(lián)系數(shù)學(xué)研究所,浙江 諸暨 311811; 2. 浙江大學(xué) 非傳統(tǒng)安全與和平發(fā)展研究中心,浙江 杭州 310058)
趙森烽-克勤概率的賭本分配研究與期望值定理
趙克勤1,2,趙森烽1
(1.諸暨市聯(lián)系數(shù)學(xué)研究所,浙江 諸暨 311811; 2. 浙江大學(xué) 非傳統(tǒng)安全與和平發(fā)展研究中心,浙江 杭州 310058)
針對概率論發(fā)展史上合理分配賭本問題,把趙森烽-克勤概率用于合理分配賭本需要的最少賭博次數(shù)研究,結(jié)果發(fā)現(xiàn),該問題中基于經(jīng)典概率得出的數(shù)學(xué)期望不會在實際中出現(xiàn),實際中出現(xiàn)的是基于趙森烽-克勤概率的“數(shù)學(xué)期望”的兩個極端值。利用趙森烽-克勤概率能客觀地反映出給定規(guī)則下最少賭博次數(shù)與最多賭博次數(shù)時的賭博結(jié)果,同時刻畫出賭博輸贏的經(jīng)典期望值和實際值,從而為有針對性地制定或修改賭博策略和合理地分配賭本提供依據(jù),在此基礎(chǔ)上給出期望值不確定定理。文中以機器人服務(wù)收費為例說明該定理的現(xiàn)實意義。
賭本分配;數(shù)學(xué)期望;趙森烽-克勤概率(聯(lián)系概率);不確定性; 期望值定理
文獻[1-3]在集對分析(set pair analysis,SPA)理論指導(dǎo)下設(shè)計和分析了一系列新的隨機試驗[4-6],先后借助“白球+黑球”隨機試驗,向指定區(qū)域隨機投針試驗、擲分幣與擲骰子隨機試驗,說明隨機性是事物相互聯(lián)系的一個屬性,隨機事件成對存在。在此基礎(chǔ)上定義了把主事件發(fā)生的概率與伴隨事件發(fā)生的概率寫成聯(lián)系數(shù)形式的聯(lián)系概率 (connection probability, CP)(也稱“趙森烽-克勤概率” (Zhao Senfeng Keqin probability, ZKP));論證了無論是古典概型概率(classical probability, CP),幾何概型概率 (geometric probability, GP),還是頻率型概率 (frequency probability, FP)都可以轉(zhuǎn)化為趙森烽-克勤概率(ZKP),從而為概率理論的創(chuàng)新研究提供了一個新的起點。文獻[7]將趙森烽-克勤概率(ZKP)應(yīng)用到風(fēng)險決策研究得到了新的風(fēng)險決策模型,文獻[8]在前述工作基礎(chǔ)上把貝葉斯概率聯(lián)系數(shù)化,得到基于貝葉斯概型的趙森烽-克勤概率,探討了趙森烽-克勤概率與“智腦”的關(guān)系。
由于如何合理分配賭本問題在概率論的形成和發(fā)展過程中起著非常重要作用,同時也有著廣泛和重要的應(yīng)用背景,特別是涉及基于趙森烽-克勤概率數(shù)學(xué)期望的現(xiàn)實性與必要性認識和期望值不確定定理,等等,本文特予專題討論。
1 如何合理分配賭本
1.1 問題描述
現(xiàn)有概率論著作對如何合理分配賭本問題的描述有不同版本[9-12]。文獻[12] 對該問題的描述如下。1654年,法國有個叫De Mere的賭徒向法國數(shù)學(xué)家帕斯卡提出如下的分賭本問題:甲、乙兩位賭徒事先約定,用擲硬幣的方式進行賭博,誰先贏3次就得到全部賭本100法郎,當(dāng)甲贏了2次,乙只贏1次時,他們不愿意賭下去,問賭本應(yīng)該如何分配?
1.2 帕斯卡解法
這個問題在當(dāng)時引起不少人興趣。有人建議按已贏次數(shù)的比例分賭本,即甲得全部賭本的2/3,乙得賭本的1/3。但有人提出異議,認為這完全沒有考慮兩個人再賭下去每人贏的可能性問題,因為這樣不符合兩人事先約定的規(guī)則,那么還要再賭幾次才能解決這個問題?法國數(shù)學(xué)家帕斯卡研究后得出的結(jié)論是:在甲贏得2次,乙只贏1次的條件下,最多只需要再玩2次可以結(jié)束這場賭博游戲;再玩2次可能出現(xiàn)的結(jié)果有以下4種(見表1)。
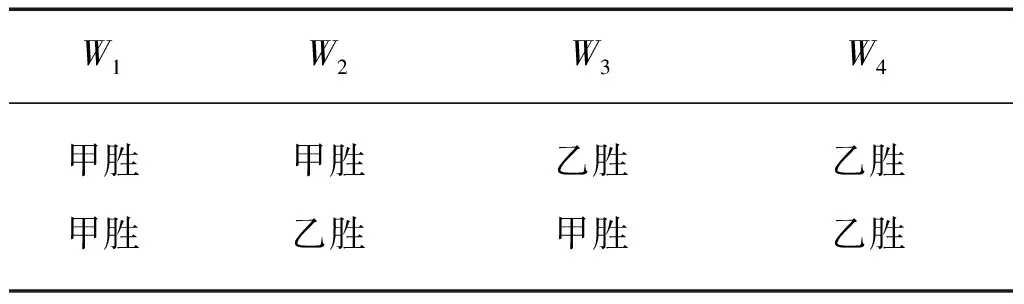
表1 游戲結(jié)果
其中前3種結(jié)果(W1,W2,W3)時甲贏得100法郎,只有當(dāng)W4發(fā)生時,甲得0法郎(即乙得100法郎),由于這4種結(jié)果是等可能的,因此在甲贏得2次,乙只贏1次的條件下,再賭下去甲得賭金X是一個隨機變量,其分布列見表2。

表 2 分布列
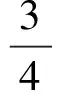
1.3 惠更斯解法
對于以上分賭本問題的帕斯卡解法,惠更斯在1657年的《賭博中的計算》一文中進一步提出一般解法,如果在u+v個等可能場合中某人有u種可能贏得a,有v種可能贏得b,則該人在u+v次賭博中可以贏得ua+vb,而每次平均可贏得
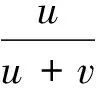

表3 X的概率分布
該人贏得的數(shù)學(xué)期望為
稱(2)式為分賭本問題的一般解法,也稱惠更斯解法。
分賭本問題的現(xiàn)實意義可以推廣為合伙投資辦廠、合作科研開發(fā)新產(chǎn)品等情況下的收益分配問題,例如,由甲、乙兩人合資經(jīng)營一個公司,一段時間后,甲乙兩人都改為單獨經(jīng)營公司或因其他原因終止合作,應(yīng)該如何分配經(jīng)營成果(如何分攤債務(wù))?
2 趙森烽-克勤概率(聯(lián)系概率)在分賭本中的應(yīng)用
2.1 趙森烽-克勤概率
趙森烽-克勤概率(聯(lián)系概率)是我們在文獻[1-3]中提出的一種新概率,其數(shù)學(xué)形式為
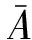
據(jù)此有

2.2 基于趙森烽-克勤概率的分賭本分析
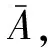
表4基于趙森烽-克勤概率的甲得賭金X的分布列
Table4AgetasweepstakescolumnofXdistributionbasedontheZhaosenfeng-Keqinprobability
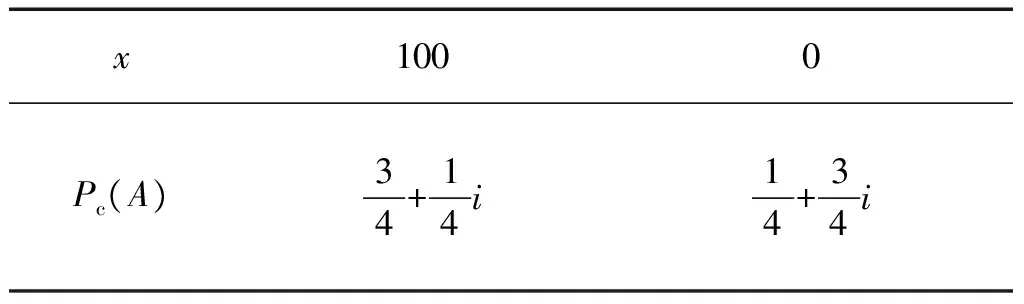
x1000Pc(A)34+14i14+34i
由表4算得甲期望得到的賭金為
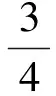
于是,問題轉(zhuǎn)化成75+25i中的i應(yīng)當(dāng)取何值的問題。結(jié)合題意和i在一般情況下的取值域[-1,1],得
當(dāng)i=1時,甲贏得賭本100法郎;
當(dāng)i=-1時,甲贏得賭本50法郎;
當(dāng)i=0時,甲贏得賭本75法朗,這是第1節(jié)中帕斯卡法的結(jié)果。
現(xiàn)在要問,在已玩3次基礎(chǔ)上最多再玩2次情況下甲有可能贏得100法郎或50法郎嗎?
我們注意到,帕斯卡在解決合理分配賭本問題時,是以最多只要再玩2次(共玩5次)就可以按約定的賭本規(guī)則結(jié)束這場賭博游戲來考慮這個問題的。這種考慮,自然地隱含著最少再玩1次(共玩4次)也有可能按約定的賭博規(guī)則結(jié)束這場賭博這樣一個問題。為此先來討論再玩1次的情況,當(dāng)甲已贏2次,乙只贏1次基礎(chǔ)上再玩1次,只有2種結(jié)果:
當(dāng)W1出現(xiàn)時,甲共贏了3次,這時甲得100法郎;當(dāng)W2出現(xiàn)時,甲、乙各贏2次,這時如果終止賭博,甲只能得50法郎,也就是不存在甲得75法郎這種情況(表5)。

表5 2種結(jié)果
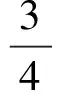
特別地,當(dāng)玩第4次時出現(xiàn)甲、乙各贏2次的局面時,甲、乙都明白,再玩1次(第5 次時),要么是甲贏(共贏3次),這時甲得100法郎,乙得0;要么是乙贏(共贏3次),這時乙得100法郎,甲得0。因此,如果甲、乙兩人都不愿冒風(fēng)險時,將選擇放棄再玩一次而終止賭博(共4次)。因此,從邏輯上說,在已玩3次基礎(chǔ)上最多再玩2次確實可按約定的規(guī)則結(jié)束賭博。但從實際出發(fā),也有可能在已玩3次基礎(chǔ)上再玩1次(共4次)就能按約定的規(guī)則結(jié)束賭博;也可以雙方協(xié)商修改規(guī)則后結(jié)束賭博,但這種情況不在本問題討論范圍內(nèi)。因此結(jié)論是:無論何種情況,甲都不可能得到75法郎。
以上分析結(jié)果表明:甲得期望賭本75法郎僅僅是一個經(jīng)典概率意義上的一個理論計算值,并不具有實際上可能出現(xiàn)的意義;具有實際出現(xiàn)意義的是50法郎或100法郎;甲在共玩3次已經(jīng)贏2次的條件下,繼續(xù)玩1次時(第4次),可能因共贏了3次得100法郎而按規(guī)則結(jié)束賭博,也可能因輸給乙而面臨再玩1次(第5次)得0法郎的風(fēng)險。
由于當(dāng)75+25i中的i=0時,75+25i=75,恰好是帕斯卡解法時甲得期望賭本,所以75+25i是一個既含有經(jīng)典期望值,又含有實際出現(xiàn)值的解集聯(lián)系數(shù)。
由此可見,以上討論的問題,表面上看是一個如何分賭本的問題,而其背后還隱藏著如何理解經(jīng)典數(shù)學(xué)期望含義和如何定義新的數(shù)學(xué)期望以及如何計算新的數(shù)學(xué)期望等問題,為此,本文在下面將給出基于趙森烽-克勤概率的數(shù)學(xué)期望定義和計算方法,并把其與經(jīng)典概率期望進行比較,討論這種新的數(shù)學(xué)期望性質(zhì),舉例說明其在實際問題中的應(yīng)用。
3 基于趙森烽-克勤概率的數(shù)學(xué)期望
3.1 數(shù)學(xué)期望
數(shù)學(xué)期望是概率論中一個極為重要的概念,文獻[10]中已指出數(shù)學(xué)期望的本質(zhì)是一種“均值”,因此被稱為“均值”更形象易懂,并分別從算術(shù)平均與加權(quán)平均2種情況說明如下。
1)算術(shù)平均
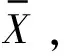
2)加權(quán)平均
如果這n個數(shù)中有相同的數(shù),不妨設(shè)其有nt個取值為xt(t=1,2,…,k),并將其列成表(見表6)。
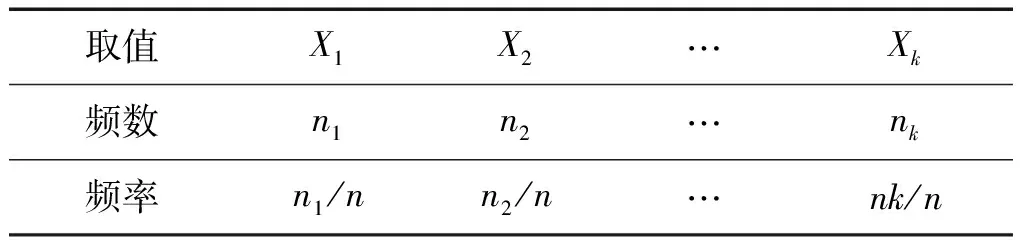
表6 Xt的頻率
這時,這n個數(shù)的“均值”為
由此得到經(jīng)典的數(shù)學(xué)期望定義如下。
定義1 設(shè)離散隨機變量X的分布列為
p(Xt)=P(X=Xt),t=1,2,…,n,…
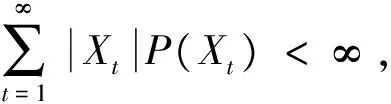
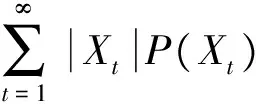
式(9)是基于隨機變量是離散型的數(shù)學(xué)期望定義。類似地,可得隨機變量是連續(xù)型時的數(shù)學(xué)期望定義, 只要將式(9)中的分布列P(Xt)改為密度函數(shù)P(X),同時把求和號改為求積號,為此有以下的定義2。
定義2 設(shè)連續(xù)隨機變量X的密度函數(shù)為p(x),如果
則稱

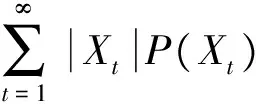
3.2 基于趙森烽-克勤概率的數(shù)學(xué)期望
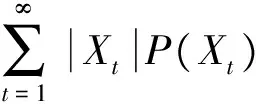
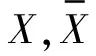
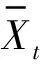
如果
則
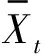
據(jù)此由式(12)得
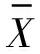
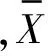
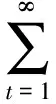
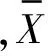
或
同理,當(dāng)式(11)成立時,對于連續(xù)隨機變量X,也同樣有式(16)成立。為節(jié)約篇幅,敘述從略。
此外要說明的是,式(16)所示的數(shù)學(xué)期望的完整意義是基于趙森烽-克勤概率的數(shù)學(xué)期望,但也可以稱為基于集對分析的聯(lián)系數(shù)學(xué)期望,在不至于引起混淆時也簡稱聯(lián)系數(shù)學(xué)期望或稱數(shù)學(xué)期望。
3.3 基于趙森烽-克勤概率的數(shù)學(xué)期望性質(zhì)
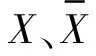
性質(zhì)1 若C是常數(shù),則
性質(zhì)2 對任意常數(shù)K,有
性質(zhì)3 對任意的兩個函數(shù)g1(x)、g2(x),有

據(jù)此聯(lián)系數(shù)學(xué)期望的性質(zhì)如下:
性質(zhì)4 若c,d是常數(shù)(c≠d,E(c)=c,E(d)=d),則有
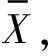
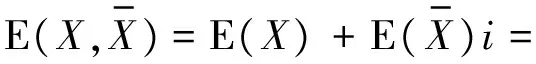

但要注意的是,由于式(21)把X的數(shù)學(xué)期望作為主事件對待,因此可以改寫成
由于隨機變量X在隨機試驗中取常數(shù)c,與此同時的事實是不出現(xiàn)性質(zhì)2。
4 數(shù)學(xué)期望值定理
基于以上討論,得到以下的數(shù)學(xué)期望值定理。
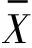
在把X作為主事件時,式(23)改寫為
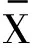
因為在式(23)~(25)中都含有隨機轉(zhuǎn)換器i,其值要根據(jù)不同情況才能確定,所以式(23)~(25)的值存在不確定性。因此,由式(23)~(25)所示的聯(lián)系數(shù)學(xué)期望值依然具有隨機性,本定理也因此稱為基于趙森烽-克勤概率的聯(lián)系數(shù)學(xué)期望不確定定理,簡稱期望值定理。
證明根據(jù)定義3中給出的基于趙森烽-克勤概率的聯(lián)系數(shù)學(xué)期望式(13)、(16)可知,式(13)和式(16)中的i是一個隨機轉(zhuǎn)換器,具有不確定性,因此式(13)和式(16)具有不確定性。
數(shù)學(xué)期望值定理從集對分析的角度說明了在隨機試驗中,不僅隨機事件成對存在,而且隨機事件的確定性與不確定性也成對存在,與之相應(yīng)的刻畫隨機事件出現(xiàn)可能性的數(shù)學(xué)期望的確定性與不確定性也成對存在。因此,在有關(guān)數(shù)學(xué)期望的眾多理論研究和實際問題的應(yīng)用中,對于數(shù)學(xué)期望的不確定性,依然需要遵循集對分析理論多年來所倡導(dǎo)的“客觀承認、系統(tǒng)描述、定量刻畫、具體分析”16字處置方針,看上去這是一種無奈之舉,但由于各種各樣的隨機事件說到底都是確定性與不確定性的對立統(tǒng)一,故唯如此,才能保證理論研究結(jié)果與實際情況的吻合[13-20]。
5 應(yīng)用
例1 計算合理分配賭本問題中甲能贏得的賭本數(shù)。
問題的描述見第1節(jié)。由1.3節(jié)介紹的惠更斯解法和式(2)知,甲的期望為
與此同時,乙的期望為
根據(jù)式(15)得
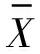
如果把甲的數(shù)學(xué)期望作為“主事件”,則可以參照式(16)把式(28)改寫成

顯然,式(29)用聯(lián)系數(shù)的形式把甲的數(shù)學(xué)期望與乙的數(shù)學(xué)期望聯(lián)系在同一個數(shù)學(xué)式中,規(guī)范地說,式(29)是甲的聯(lián)系數(shù)學(xué)期望,也簡約地稱為甲的數(shù)學(xué)期望。
根據(jù)題意把u=3,v=1,a=100,b=0代入式(29)和式(26)得
由于式(30)與式(31)相等,以下僅對式(31)計算分析。
當(dāng)i=-1時,得Ec(X)=75+25i=50
(32)
當(dāng)i=1時,得Ec(X)=75+25i=100
(33)
前面的2.2中已通過計算與分析證實甲可以期望實現(xiàn)的贏得賭本數(shù)為50法郎或100法郎,不可能期望實現(xiàn)的贏得賭本數(shù)為75法郎,為此令
解式(25)得i=0。也就是說,式(29)中的i取0沒有實際意義,但所對應(yīng)的聯(lián)系數(shù)學(xué)期望值75法郎恰恰是經(jīng)典概率意義下的數(shù)學(xué)期望值。
例2 機器人月租金期望。
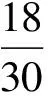
利用式(9)得
E(X)=3 000×(0.6+0.4i)+5 000×

于是問題轉(zhuǎn)化成如何確定其中的i值。
顯然max E(X)=5 000,min E(X)=3 000。于是,3 800+4 200i=5 000,解得i=0.285 7;3 800+4 200i=3 000, 解得i=-0.190 5。由此得i∈[-0.190 5,0.285 7],取i的平均值為0.238 1,代入式(35)得4 800元。這說明,該機器人服務(wù)公司通過適當(dāng)調(diào)度出租該機器人,可以期望得到月租金4 800元。與之相應(yīng)的出租天數(shù)x(為企業(yè)服務(wù)天數(shù))與y(為家庭服務(wù)天數(shù))只需解以下方程
解得,y=1天,x=29天。
6 結(jié)束語
本文從討論概率論發(fā)展史上如何合理分賭本問題入手,研究了數(shù)學(xué)期望的不確定性及其聯(lián)系數(shù)表達。雖然在概率論中早就指出數(shù)學(xué)期望是一種關(guān)于隨機變量的均值,但本文是首次給出數(shù)學(xué)期望不確定定理和這一定理的實際意義。由于經(jīng)典概率意義下的數(shù)學(xué)期望值在隨機試驗中可能出現(xiàn)也可能不出現(xiàn),而一些實際問題極需要針對可能出現(xiàn)的極大極小數(shù)學(xué)期望值作出決策,基于這一事實,我們提倡在有關(guān)隨機決策之類問題的研究中大膽地應(yīng)用本文給出的基于趙森烽-克勤概率的聯(lián)系數(shù)學(xué)期望,因為聯(lián)系數(shù)學(xué)期望不僅包含了經(jīng)典的數(shù)學(xué)期望值,還包含了可能出現(xiàn)的其他期望值,特別是,對各種可能出現(xiàn)的其他期望值的分析過程中,還在有意無意地引導(dǎo)人們?nèi)リP(guān)注和分析導(dǎo)致不同期望值出現(xiàn)的那些不確定性因素,這對于提高隨機決策的科學(xué)性與針對性至關(guān)重要。至于有關(guān)聯(lián)系數(shù)學(xué)期望的運算規(guī)則、聯(lián)系數(shù)學(xué)期望與隨機變量方差的關(guān)系、聯(lián)系數(shù)學(xué)期望與大數(shù)定律關(guān)系,等等問題,我們將在后續(xù)文章中討論。
[1]趙森烽,趙克勤.概率聯(lián)系數(shù)化的原理與聯(lián)系概率在概率推理中的應(yīng)用[J].智能系統(tǒng)學(xué)報, 2012, 7(3): 200-205.
ZHAO Senfeng, ZHAO Keqin. The principle of the probability of connection number and application in probabilistic reasoning[J]. CAAI transactions on intelligent systems, 2012, 7(3): 200-205.
[2]趙森烽,趙克勤.幾何概型的聯(lián)系概率與概率的補數(shù)定理[J].智能系統(tǒng)學(xué)報, 2013, 8(1): 11-15.
ZHAO Senfeng, ZHAO Keqin. Contact probability (complex probability) of geometry probability and probability of the complement number theorem[J]. CAAI transactions on intelligent systems, 2013, 8(1): 11-15.
[3]趙森烽,趙克勤. 基于頻率的趙森烽-克勤概率與隨機事件的轉(zhuǎn)化定理[J]. 智能系統(tǒng)學(xué)報, 2014, 9(1): 53-69.
ZHAO Senfeing, Zhao Keqin. Probability based on the frequency and random events transformation theorem[J]. CAAI transactions on intelligent systems, 2014,9(1):53-69.
[4]趙克勤.集對分析及其初步應(yīng)用[M].杭州:浙江科學(xué)技術(shù)出版社, 2000: 1-198.
[5]趙克勤, 宣愛理. 集對論——一種新的不確定性理論方法與應(yīng)用[J]. 系統(tǒng)工程, 1996, 14(1): 18-23.
Zhao Keqin, Xuan Aili. Set pair theory—a new theory method of non-define and its applications[J]. Systems engineering, 1996, 14(1): 18-23.
[6]趙克勤.集對分析的不確定性理論在AI中的應(yīng)用[J].智能系統(tǒng)學(xué)報, 2006, 1(2): 16-25.
ZHAO Keqin.The application of uncertainty systems theory of set pair analysis (SPA)in the artiartificial intelligence[J].CAAI transactions on intelligent systems, 2006,1(2):16-25.
[7]趙森烽,趙克勤. 聯(lián)系概率的由來及其在風(fēng)險決策中的應(yīng)用[J].數(shù)學(xué)的實踐與認識, 2013, 43(4): 165-171.
ZHAO Senfeng, ZHAO Keqin. The contact probability in risk decision-making medium application [J].Mathematics in practice and theory, 2013, 43(4): 165-171.
[8]趙克勤,趙森烽.貝葉斯概率向趙森烽-克勤概率的轉(zhuǎn)換與應(yīng)用[J].智能系統(tǒng)學(xué)報, 2015, 10(1): 51-61.
ZHAO Keqin, ZHAO Senfeng. Bayes probability transition to Zhao Senfeng-Keqin probability and its application[J]. CAAI transactions on intelligent systems, 2015, 10(1): 51-61.
[9]王梓坤.概率論基礎(chǔ)及其應(yīng)用[M].北京:科學(xué)出版社, 1979: 1-218.
[10]趙秀恒,米立民.概率論與數(shù)理統(tǒng)計[M].北京:高等教育出版社, 2008: 53-55.
[11]孫榮恒.趣味隨機問題[M].北京:科學(xué)出版社, 2009: 18-19.
[12]茆詩松,程依明,濮曉龍.概率論與數(shù)理統(tǒng)計教程[M].北京:高等教育出版社, 2011: 77-85.
[13]趙克勤.集對分析與熵的研究[J].浙江大學(xué)學(xué)報: 社科版, 1992, 38(2): 65-72.
ZHAO Keqin. Set pair analysis and entropy research[J].Journal of Zhejiang university: social science edition, 1992, 38(2): 65-72.
[14]趙克勤.集對分析及其初步應(yīng)用[J].大自然探索, 1994, 13(1): 67-72.
ZHAO Keqin. Set pair analysis and its preliminary application[J].Exploration of nature, 1994, 13(1): 67-72.
[15]趙克勤.集對分析對不確定性的描述和處理[J].信息與控制, 1995, 24(3): 162-166.
ZHAO Keqin. Disposal and discription of uncertainties based on the Set pair analysis[J].Information and control, 1995, 24(3): 162-166.
[16]趙克勤.試論集對分析與概率論的關(guān)系[C]//中南模糊系統(tǒng)與數(shù)學(xué)論文集. 長沙: 湖南科技出版社, 1995: 253.
[17]趙克勤.二元聯(lián)系數(shù)A+Bi的理論基礎(chǔ)與基本算法及在人工智能中的應(yīng)用[J].智能系統(tǒng)學(xué)報,2008, 3(6): 476-486.
ZHAO Keqin. Thetheoretical basis and basic algorithm of binary connectionA+Biand its application in AI[J].CAAI transactions on intelligent systems, 2008, 3(6): 476-
486.
[18]趙克勤,趙森烽.奇妙的聯(lián)系數(shù)[M].北京:知識產(chǎn)權(quán)出版社, 2014: 1-206.
[19]劉秀梅,趙克勤.區(qū)間數(shù)決策集對分析[M].北京:科學(xué)出版社, 2014: 1-214.
[20]蔣云良,趙克勤,劉以安,等.信息處理集對分析[M].北京:清華大學(xué)出版社, 2015: 1-228.

趙克勤,男,1950年生,研究員,主要研究方向為信息處理、集對分析、聯(lián)系數(shù)學(xué)、聯(lián)系科學(xué)。浙江大學(xué)非傳統(tǒng)安全與和平發(fā)展中心集對分析研究所所長,原中國人工智能學(xué)會第5、6、7三屆學(xué)會理事,人工智能基礎(chǔ)專業(yè)委員會副主任,集對分析聯(lián)系數(shù)學(xué)專業(yè)籌備委員會主任;1989年提出集對分析(聯(lián)系數(shù)學(xué)),發(fā)表學(xué)術(shù)論文100余篇,出版專著3部。

趙森烽,男,1993年生,碩士研究生,主要研究方向為信息處理、集對分析聯(lián)系數(shù)學(xué)。發(fā)表學(xué)術(shù)論文6篇。
DistributionofgamblingcapitalandexpectationvaluetheoremforZhaoSenfeng-Keqinprobability
ZHAO Keqin1,2, ZHAO Senfeng1
(1. Zhuji Institute of Connection Mathematics, Zhuji 311811, China; 2.Center for Non-traditional Security and Peaceful Development Studies, Zhejiang University, Hangzhou 310058, China)
With respect to the reasonable distribution of gambling capital in the developmental history of probability theory, Zhao Senfeng-Keqin probability has been used to investigate the minimum number of gambling times necessary for the rational allocation of the minimum amount of gambling capital. Results have shown that the mathematical expectation for this problem, based on classical probability, failed to occur in practice. What appeared instead are two extreme values of “mathematical expectation” based on the Zhao Senfeng-Keqin probability, which can objectively reflect the gambling results within the smallest and largest number of gambling times for a given rule. In addition, it describes both the classic expectation value and the actual value, thereby providing a basis for formulating or amending specific gambling tactics and the reasonable allocation of gambling capital. The result is an uncertainty theorem for the expectation value. In this paper, we illustrate the practical significance of this theorem by giving an example of service charging on a robot.
distribution of gambling capital; mathematical expectation; Zhao Senfeng-Keqin probability (contact probability); uncertainty; expectation value theorem
10.11992/tis.201604020
http://kns.cnki.net/kcms/detail/23.1538.TP.20170626.1739.006.html
TP18
A
1673-4785(2017)05-0608-08
中文引用格式:趙克勤,趙森烽.趙森烽-克勤概率的賭本分配研究與期望值定理J.智能系統(tǒng)學(xué)報, 2017, 12(5): 608-615.
英文引用格式:ZHAOKeqin,ZHAOSenfeng.DistributionofgamblingcapitalandexpectationvaluetheoremforZhaoSenfeng-KeqinprobabilityJ.CAAItransactionsonintelligentsystems, 2017, 12(5): 608-615.
2016-04-18. < class="emphasis_bold">網(wǎng)絡(luò)出版日期
日期:2017-06-26.
國家社科基金重大項目(12amp;ZD099).
趙克勤. E-mail:spacnm@163.com.

