“幾何畫板”可以這樣玩

文︳李超貴

“幾何畫板”可以這樣玩

文︳李超貴

幾何畫板作為一款簡單易學的數學軟件，體型小巧卻功能強大，可以為數學教學創設一個“做數學”的環境，開展數學實驗，打造探究課堂，因而受到廣大數學教師的青睞。筆者作為一名幾何畫板的忠實粉絲，也積累了一些使用心得，現略舉一二。

一、開展數學實驗，打造探究課堂

我們為了獲得某種數學結論、檢驗某個數學猜想、解決某類實際問題時，可以利用幾何畫板的構造、計算、度量等功能創設“做數學”的環境，引導學生的數學思維積極參與，開展數學實驗，打造探究課堂。

如對“兩個三角形中有五個元素分別相等，那么這兩個三角形一定全等嗎？”這個問題的探究，可以設計實驗探究活動——

探究1.請構造出一對三角形，它們有五個元素分別相等，但這兩個三角形卻不全等；

探究2.這樣的三角形有多少對？能否找到一般性的構造方法？

根據兩個三角形全等的判定定理，這五個元素只可能是三個角、兩條邊，否則一定是全等的。問題的關鍵是我們可否構造出相應的反例。很顯然，圖1所示的一對三角形有五個元素分別相等，但它們不全等。

為了進一步探究這類三角形，我們可以在幾何畫板中搭建如下實驗平臺：

第一步，新建參數 k，a（k＞0，a＞0），初始值k=1.200（注意調節參數屬性，使數值精確度為千分之一，參數的鍵盤調節幅度為0.001），a=2.00；

第二步，計算 ka，k2a，k3a，并分別畫出長為 a，ka，k2a，k3a的四條線段；

第三步，畫線段AB=a，分別以A，B為圓心，以k2a和ka為半徑畫圓，記其中一個交點為C，再畫線段DE=ka，分別以D，E為圓心，以k3a和k2a為半徑畫圓，記其中一個交點為F（如圖2所示）；

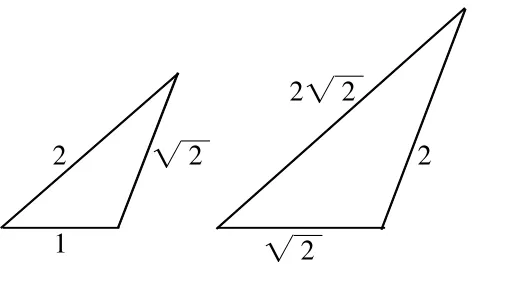
圖1

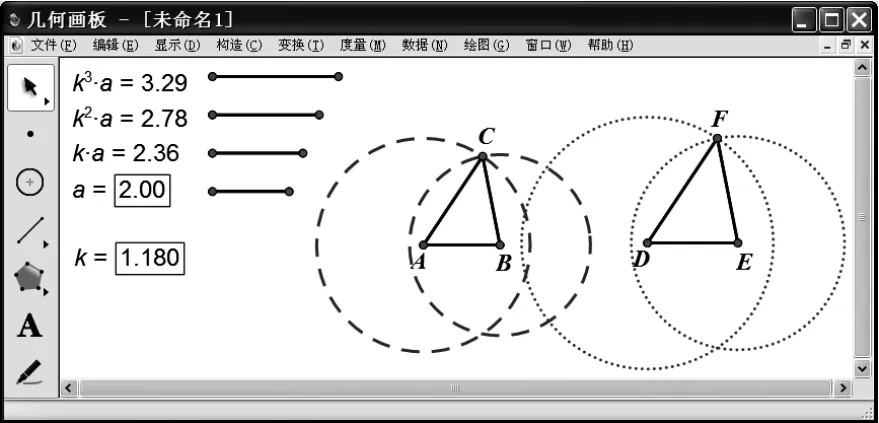
圖2

第四步，改變參數a，k的值，觀察圖形的變化。

通過觀察實驗現象，我們可以發現分別以a，ka，k2a和 ka，k2a，k3a為邊的兩個三角形是符合條件的，它們是一對相似三角形，k是它們的相似比，用這種方法可以構造出無數多組這樣的三角形。

那么，是否對于任意的參數a，k都可以構造出滿足條件的一對三角形呢？通過實驗我們會發現，當一對三角形構造出來后，僅改變a的值，只是改變一對三角形的大小。但當參數a固定，參數k變化到某個范圍之外時，三角形并不存在（如圖3、圖 4所示）。

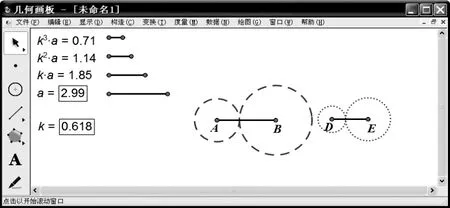
圖3

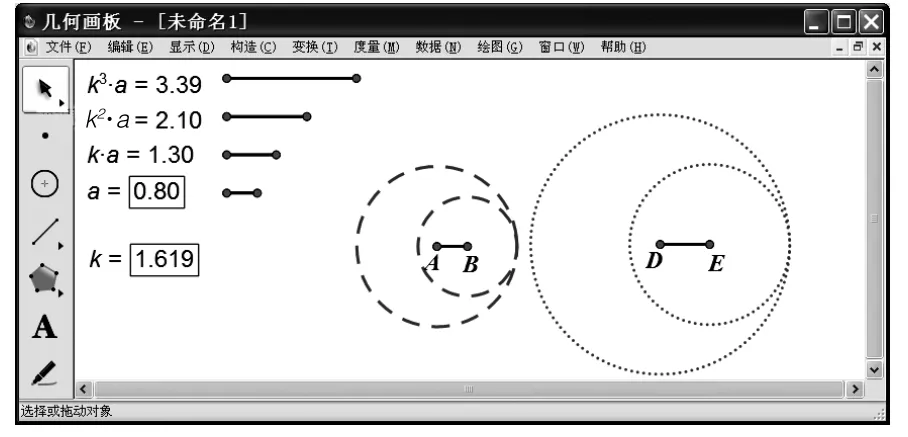
圖4

通過對實驗現象的進一步思考，我們發現分別以 a，ka，k2a和 ka，k2a，k3a 為邊構造三角形還需要滿足三角形三邊的一個基本關系，那就是“三角形任意兩邊之和大于第三邊”。由此我們不難得到

二、輔助問題解決，促進命題創新

一些數學問題看起來可能很棘手，找不到解決的突破口，但利用幾何畫板先做一些定性的分析，往往會打開思路，甚至會有一些出人意料的發現。再通過定量計算或設計，就可以達到命題創新的目的。

如長沙市2017年中考試卷中有這樣一道選擇題：如圖5，將正方形ABCD折疊，使頂點A與CD邊上的一點H重合（H不與端點C，D重合），折痕交AD于點E，交BC于點F，邊AB折疊后與邊BC交于點G，設正方形 ABCD的周長為 m，的值為（ ）。

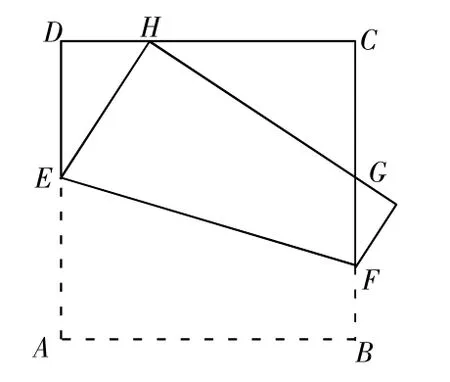
圖5

本題若要通過計算手段找到△CHG的周長與正方形ABCD的周長間的關系并不簡單，但如果用測量等實驗手段找到答案并不困難。在幾何畫板中，選擇正方形ABCD邊CD上的動點H，構造出題中圖形，測量出△CHG的周長值，再拖動點H，發現測量值不改變，說明△CHG的周長并不隨點H位置的變化而變化。再測量出正方形ABCD的周長，并計算△CHG的周長與正方形ABCD的周長的比，結果為0.5（如圖6所示）。

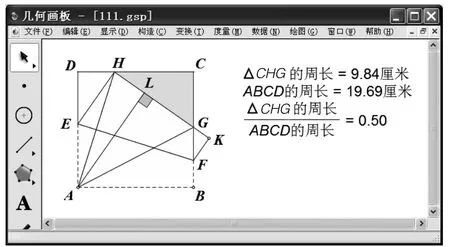
圖6

實際上，過點A作AL⊥GH于點L，容易證得 Rt△ADHRt△ALH，Rt△ABGRt△ALG，于是DH=LH，BG=LG，這說明△CHG的周長等于BC+CD，恰好就是正方形ABCD的周長的一半。

在上面的問題中，△CHG的周長是一個不變量，由 Rt△ADHRt△ALH，Rt△ABGRt△ALG不難發現∠GAH的大小也是一個不變量（45°）。當然也有許多量隨著H點位置的變化而變化，如四邊形EFKH的面積，那么它的變化有什么規律呢？利用幾何畫板可以做進一步探索。

如圖7所示，先度量出DH的距離x，四邊形EFKH 的面積 S，依次選擇 x，S，在“繪圖”菜單中繪制點 P（x，S），再選擇點 H，在“構造”菜單中選擇“軌跡”，得到一個S關于x的函數圖像，直觀反映出四邊形EFKH的面積S隨H點位置變化的規律。分析圖像特征，可以斷定這是一個二次函數的圖像。類似地，我們還可以研究四邊形EFKH的周長、△AGH的面積，等等。

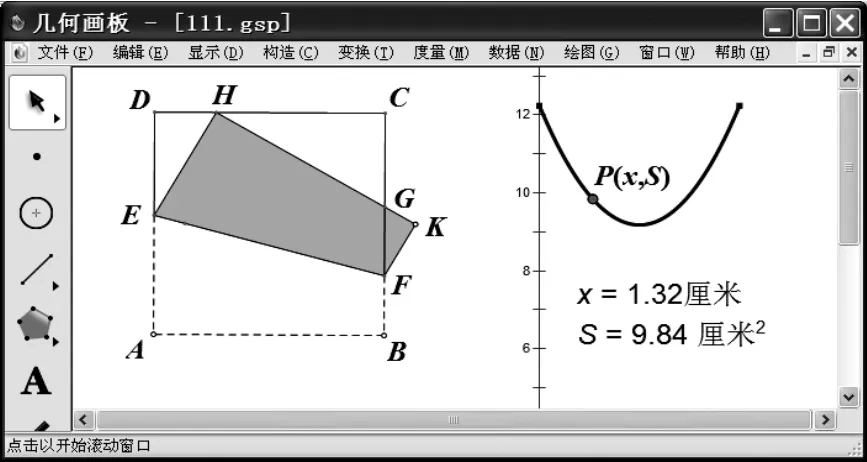
圖7

通過上面的實驗探究、定性分析，接下來做一些定量計算，我們可以設計一組新的問題：

如圖8所示，現有一張邊長為4的正方形紙片ABCD，點H為正方形CD邊上的一點（不與點 C、點 D重合），將正方形紙片折疊，使點A落在H處，點B落在K處，折痕為EF，連接AH。

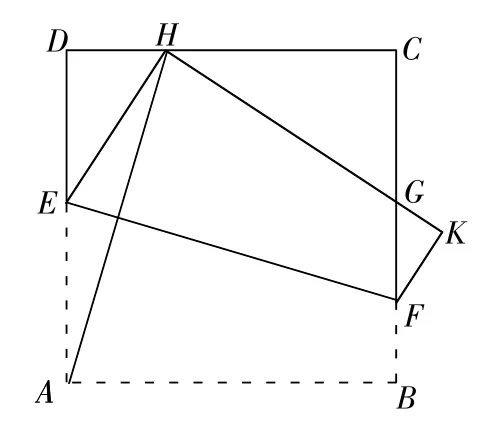
圖8

（1）求證：∠AHD=∠AEF；

（2）求證：△CHG的周長為定值；

（3）設DH的長為x，四邊形EFKH的面積為S，求出S與x的函數關系式，試問S是否存在最小值？若存在，求出這個最小值；若不存在，請說明理由。

（4）當點H移動時，設△DEH的周長為L1，△KGF的周長為L2，判斷L1+L2是否為定值，為什么？

（5）設DH的長為x，△DEH的面積為S1，△KGF的面積為S2，S0=S1+S2，求出S0與x的函數關系式，試問S0是否存在最大值？若存在，求出這個最大值；若不存在，請說明理由。

有了前面的實驗手段作定性分析，再通過合情推理、定量計算，解決上面這組問題并不困難，讀者不妨嘗試一下，或許還有更多的發現。

幾何畫板是我們數學老師的好幫手，只要我們細心琢磨，還會玩出更多的花樣。特別是我們把它當作一個數學實驗的平臺的時候，它的魅力會激發我們獲得更多的發現與創造。

（作者單位：長沙市雨花區教育科學研究所）