柔性欠驅動機械臂動力學耦合分析

劉建英 王效岳 宮金良

山東理工大學機械工程學院，淄博,255049

柔性欠驅動機械臂動力學耦合分析

劉建英 王效岳 宮金良

山東理工大學機械工程學院，淄博,255049

為建立柔性3R欠驅動機械臂的動力學方程，采用Euler-Bernoulli梁模型并添加經迭代計算的邊界條件，對柔性機械臂進行了動力學耦合與仿真分析。在對柔性機械臂進行模態分析的基礎上，將柔性機械臂視為包含邊界條件的懸臂梁和簡支-自由梁模型，采用假設模態法建立柔性3R欠驅動機械臂的動力學模型。仿真結果證明：添加經迭代計算的邊界條件的柔性梁模型能更好地反映自由關節的加速度耦合情況。最后對柔性欠驅動機械臂與剛性欠驅動機械臂進行關節耦合指標分析，結果表明柔性欠驅動機械臂的自由關節包含更復雜的耦合情況，對柔性機械臂彈性振動的控制是對柔性欠驅動機械臂控制的關鍵。

欠驅動；柔性機械臂；彈性變形；耦合分析

0 引言

近年來機器人及其應用已成為研究焦點，成果也越來越多[1-3]。柔性欠驅動機器人兼具柔性機器人與欠驅動機器人的優點，其質量小、負載大、耗能低、結構緊湊、運動靈活且具有豐富的動力學特性等[4-5]。常用的柔性機器人的建模方法有假設模態法[6-7]和有限元法[8]。假設模態法建立的動力學方程含有較少的廣義變量，因此常用于柔性機械系統的動力學建模與控制。

柔性欠驅動機械系統不同于剛性欠驅動機械系統，其大范圍轉動與機械臂的彈性變形相互耦合[9]，運動的不確定性大，因此有必要建立更符合實際情況的動力學模型。由于柔性機械臂兩端的受力情況較復雜，理想的懸臂梁或者簡支梁模型與其真實變形相差較大，因此會影響假設模態法建模的精確性。本文使用的歐拉梁模型依據ADAMS對實物模型的分析結果，計算出合適的柔性梁的邊界條件，提高了動力學模型的精度。

對欠驅動機械系統的動力學耦合分析，揭示了自由關節的運動本質[10]。耦合分析結果一方面可以指導機械系統的結構設計，選取合適的關節作為自由關節和驅動關節;另一方面對于冗余自由度的機械系統，選擇耦合度高的關節驅動，達到相同任務，可以減少能量消耗。因此，對柔性欠驅動機械系統進行動力學耦合分析是很有意義的。本文針對柔性3R欠驅動機械臂，對比分析了在考慮和不考慮機械臂彈性變形的情況下，自由關節的單關節和全局耦合指標。

1 柔性機械臂的動力學建模

1.1柔性機械臂的變形描述與離散

將柔性機械臂作為剛柔耦合構件進行分析，柔性機械臂簡化為兩端剛體和中間柔性梁。平面柔性3R欠機械臂的抽象模型如圖1所示。

圖1 柔性3R欠驅動機械臂模型Fig.1 Flexible 3R underactuated manipulator model

圖1中第一個柔性機械臂，半徑為a1的圓柱形剛體表示連接電機和柔性桿的固定座。第二個柔性臂的驅動電機和編碼器視為半徑為b1的圓柱剛體，添加在第一個柔性臂的末端。機械臂末端機械手的質量視為半徑為b3的圓柱形剛體,添加在第三個柔性臂末端。三個柔性機械臂簡化為相同的兩端剛體和中間柔性桿模型，如圖2所示。

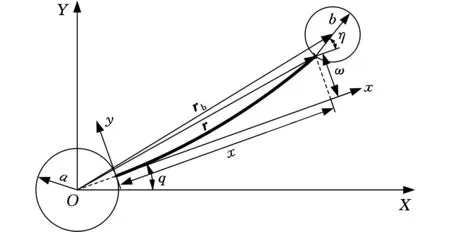
圖2 柔性機械臂的變形描述Fig.2 Deformation description of flexible manipulator

圖2中，OXY為慣性坐標系，ω為柔性梁的橫向彎曲變形量。r為柔性梁質點矢徑，rb為柔性機械臂末端剛體矢徑，q為關節轉角，則柔性梁上某一點的位置向量

R1=A1r1=A1[a1+xω]

(1)

柔性梁末端剛體中心的位置向量

Rb1=A1rb1=A1[a1+l1+b1cosη1ω1+b1cosη1]

(2)

其中，l表示柔性梁的長度，下標1、2、3對應三個柔性機械臂。

A1為第一個柔性臂所在的牽連坐標系到慣性坐標系下的變換矩陣，即

式中，θ1為固定在第一個柔性臂上的牽連坐標系與慣性坐標系的夾角。

在假設柔性梁小變形的條件下，柔性梁橫向變形引起的轉角η滿足條件：

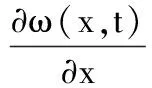
tanη=cosη=ω′ sinη=0

式中，ω′為柔性梁的變形量對柔性梁長度x的求導；t為時間。

由此可得

Rb1=A1rb1=A1[a1+l1+b1η1ω1+b1η1]

(3)

θ1=q1θ2=q1+q2+ω1′

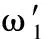
用假設模態法對柔性梁進行離散[11]，即

ω(x,t)=Φ(x)σ(t)

(4)

其中，Φ(x)為橫向振動模態函數行向量，模態函數由梁的邊界條件決定；σ(t)為橫向振動模態坐標列向量，模態坐標由梁的初始條件決定；φ1、φ2、φ3為柔性梁橫向振動的前三階模態函數，δ1、δ2、δ3為柔性梁橫向振動的前三階模態坐標。

對柔性機械臂進行模態分析，根據不同邊界條件對柔性梁模態振動的影響規律，選定對應Euler-Bernoulli梁的邊界條件。利用模態分析的前兩階數據進行迭代計算，得到邊界條件的具體值。

對柔性梁的邊界條件進行優化：對于第一、第二個柔性機械臂，柔性機械臂前一關節是驅動關節，因此將機械臂的柔性部分視為包含邊界條件的懸臂梁。模態分析結果與理想的懸臂梁模型進行比較，第一階模態頻率明顯減小，二階及更高階模態頻率增大。根據邊界條件對懸臂梁的影響規律，選用包含末端集中質量和扭轉彈簧的懸臂梁模型。對于前五階模態頻率，含有邊界條件的Euler-Bernoulli梁模型的模態計算結果與模態分析結果可以保持在較小誤差范圍內，所以此模型比理想懸臂梁模型更能表現柔性臂的變形。

對于第三個柔性機械臂，因為它的前一關節是自由關節，所以將機械臂的柔性部分視為包含邊界條件的簡支-自由梁模型。分析過程同上，最終選用簡支端含有轉動慣性元件和扭轉彈簧，自由端含有集中質量的簡支-自由梁模型。對于前五階模態，此模型的模態計算結果與分析結果的誤差可以保持在較小范圍內，所以此模型比理想的簡支-自由梁模型更能表現柔性臂的變形。添加經迭代計算邊界條件的柔性梁模型，下文稱之為優化后的柔性梁模型。

柔性梁上質點在笛卡兒坐標系下的矢量為

R1=Ar1R2=A1rb1+A2r2

R3=A1rb1+A2rb2+A3r3

柔性梁末端在慣性坐標系下的矢量為

Rb1=A1rb1Rb2=A1rb1+A2rb2

Rb3=A1rb1+A2rb2+A3rb3

本文柔性3R欠機械臂參數為：三個柔性梁的長度、高度、厚度和密度相同，li=0.22 m；hli=0.03 m；dli=0.004 m；ρli=2800 kg/m3；三個柔性機械臂中心剛體半徑、高度與密度相同，ai=0.03 m；hai=0.03 m；ρai=2800 kg/m3；三個柔性機械臂末端剛體半徑、高度與質量相同，bi=0.03 m；hbi=0.03 m；mbi=1.2 kg；其中，i=1,2,3。

三個柔性梁的模態頻率特征值數據見表1、表2。

表1 柔性梁模態頻率

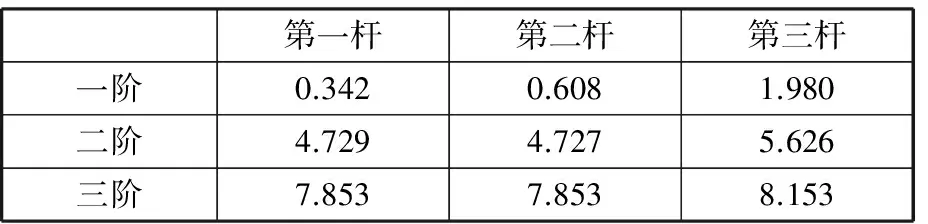
表2 柔性梁特征值

1.23R柔性欠驅動系統的動能和勢能

第i個柔性機械臂的的動能

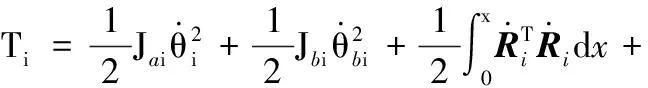
(5)

式中，Jai為第i個柔性機械臂的轉動慣量。

柔性機械臂的勢能為柔性梁的彎曲勢能，即

(6)

1.33R柔性機械臂的動力學方程

將計算出的動能和勢能代入拉格朗日方程中，有

(7)

L=T1+T2+T3-V1-V2-V3

式中，Q為系統的廣義外力。

系統的廣義變量

(8)

其中，qi為第i個機械臂與前一個機械臂延長線的夾角,i=1,2,3。(σ1，σ2，σ3)T是三維列向量。

求解后得到動力學方程的矩陣形式為

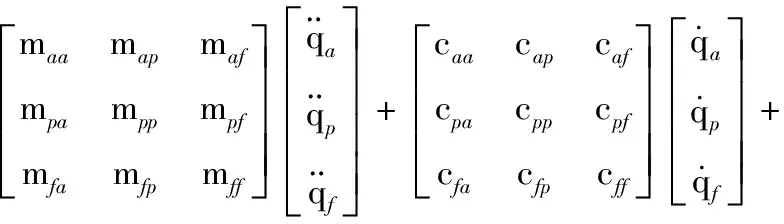
(9)

其中，qa為驅動關節；qp為自由關節；qf為彈性廣義變量。式(9)等號左邊第一項為質量矩陣對應的慣性力；第二項為廣義速度的二次矩陣，其中元素為c，包含離心力、哥式力；第三項為剛度矩陣，其中元素為k，對應保守力；第四項為機械臂彈性變形產生的慣性力矩陣， 包含Qa，Qp，Qf；等號右邊為廣義外力，τa為主動關節的驅動力；τp為自由關節的驅動力，且τp=0；τf為彈性廣義坐標對應的廣義力。

2 柔性欠驅動機械臂的耦合分析與仿真

2.1關節耦合指標分析

欠驅動系統自由關節運動的本質是主動關節通過運動耦合間接驅動其轉動。對系統進行動力學耦合分析，可以揭示欠驅動系統的運動規律。對于柔性欠驅動機械系統，由于機械臂存在彈性變形，在其運動過程中機械臂的彈性變形和大范圍轉動之間又存在耦合關系，柔性欠驅動機械系統運動的耦合程度復雜，所以對柔性欠驅動機械系統的耦合分析也更加必要。

(10)

其中，Dc表示主動、被動關節加速度關系，ζi為Dc的奇異值，則自由關節的耦合指標為[12]

(11)

為了得到不同位型下柔性機械臂的耦合指數，令q1=0。圖3是柔性機械臂關節速度為零時，三關節的耦合曲面。

圖3 速度為0時三個關節耦合指數Fig.3 Coupling index of three joints at zero speed

圖3中，三個曲面從上到下依次為第三關節、第二關節、第一關節的耦合指數。當關節角速度為零時，柔性機械臂無彈性變形，柔性機械臂的耦合指數與剛性機械臂相同。

由圖3及表3數據可知，顯然第三關節為自由關節時，系統耦合值較大。因此柔性3R欠驅動機械臂采用第三關節為自由關節更合理，自由關節更容易被運動耦合驅動。

表3 速度為0時三個關節的耦合指標參數

圖4所示為使用優化后的柔性梁模型計算的第三關節耦合指數受速度影響曲面。由圖4可知，速度較低時，耦合指數隨關節變化較小。當速度增大時,自由關節的耦合指數隨關節角度改變呈階躍性變化，在一定范圍內速度越大,耦合值的階躍現象越明顯。因為當關節轉速變大時，柔性機械臂的彈性變形增大，彈性變形使得耦合指數變化變得不規則,因此柔性欠驅動機械臂的耦合運動規律比剛性欠驅動機械臂更復雜。

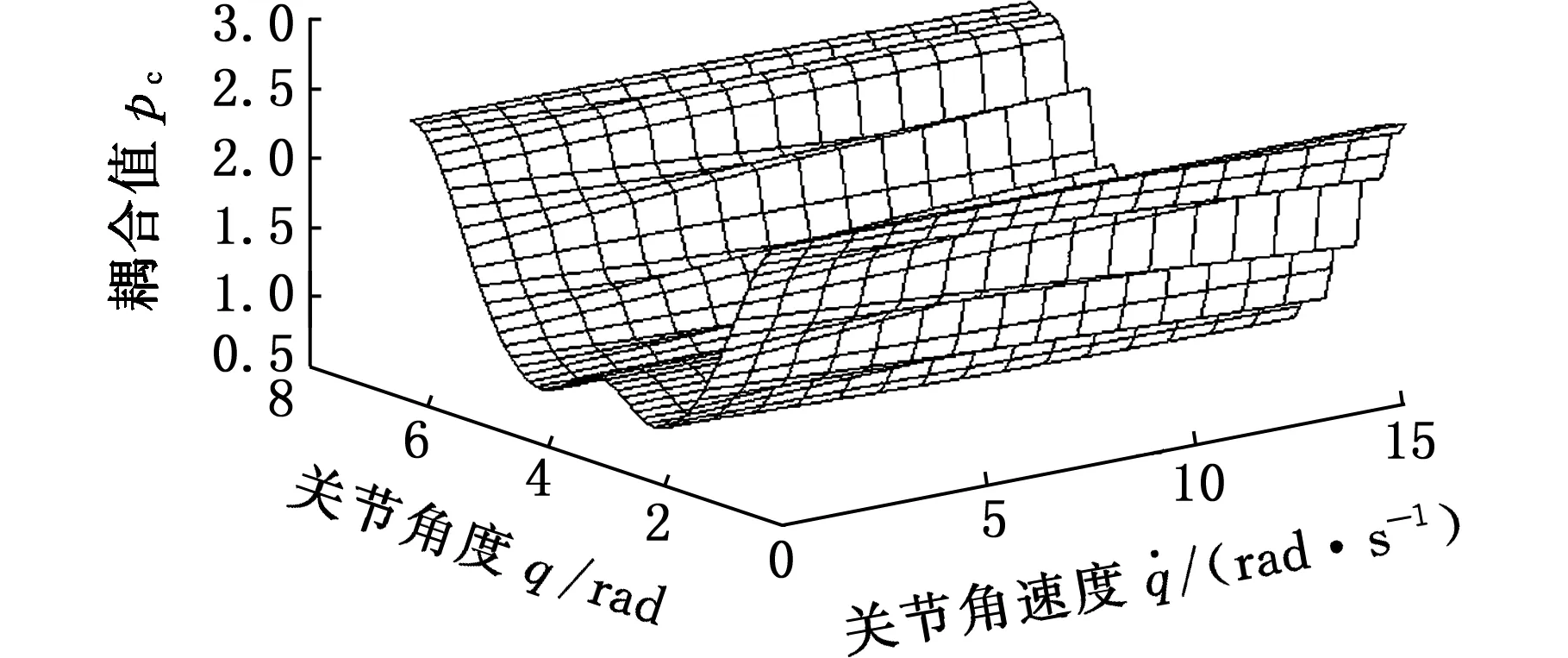
圖4 優化后的第三關節耦合指數曲面Fig.4 The third joint coupling index surface optimization

圖5 未優化的第三關節耦合指數曲面Fig.5 The third joint coupling index surface without optimization

圖5為使用未優化的柔性梁模型計算的第三關節耦合指數受速度影響曲面。由圖5可知，當關節角速度增大時，耦合指數幾乎不變。這說明使用未優化的柔性梁模型進行關節耦合分析，不能很好地體現彈性變形對耦合指數的影響。

2.2柔性欠驅動機械臂仿真

在不考慮動力學方程中速度二次型項的情況下，自由關節的運動由主動關節的加速度耦合驅動，因此，分別對剛性和柔性欠驅動機械臂的自由關節進行加速度仿真，可體現出彈性變形對加速度耦合的影響。

根據圖1的抽象模型，建立柔性機械臂的ADAMS模型，如圖6所示。

圖6 柔性機械臂的ADAMS模型Fig.6 ADAMS model of flexible manipulator

根據上文描述，三個柔性機械臂的ADAMS模型相同。柔性梁在ANSYS中劃分單元，并生成包含模態數據的中間文件，將中間文件導入到ADAMS中，完成建模。在三個關節處添加轉動副，在第一、第二個關節處添加驅動力矩，大小為0.5sintN·m。相同條件下建立剛性欠驅動機械臂模型。圖7、圖8為被動關節的角速度和角加速度仿真結果對比。

圖7 自由關節的角速度Fig.7 Angular velocity of free joints

圖8 自由關節的角加速度Fig.8 Angular acceleration of free joints

由圖7、圖8可知，時間大于4 s后，自由關節的角速度的幅值變大，柔性機械臂和剛性機械臂的角速度和角加速度差距變大。

由圖4可知，當關節角速度增大時，柔性機械臂的彈性變形對自由關節的耦合指標影響較大。而關節耦合指標反映的是關節之間加速度耦合程度，所以關節耦合指標的變化會同時影響自由關節的角速度和角加速度。

與剛性欠驅動機械臂相比，柔性欠驅動機械臂的最大特點是彈性變形影響了自由關節的耦合值指標。因為彈性變形對耦合指標的影響明顯，故不能忽略。從而證明了當Euler-Bernoulli模型添加了經迭代計算后的邊界條件，其耦合指數計算結果能更好地反映ADAMS的仿真結果。

3 機械臂的耦合指標對比分析

3.1單關節耦合指標對比分析

考慮自由關節分別與單個主動關節之間的耦合關系,將式(10)寫成：

(12)

則有

pci,j=|Dci,j|j=1,2

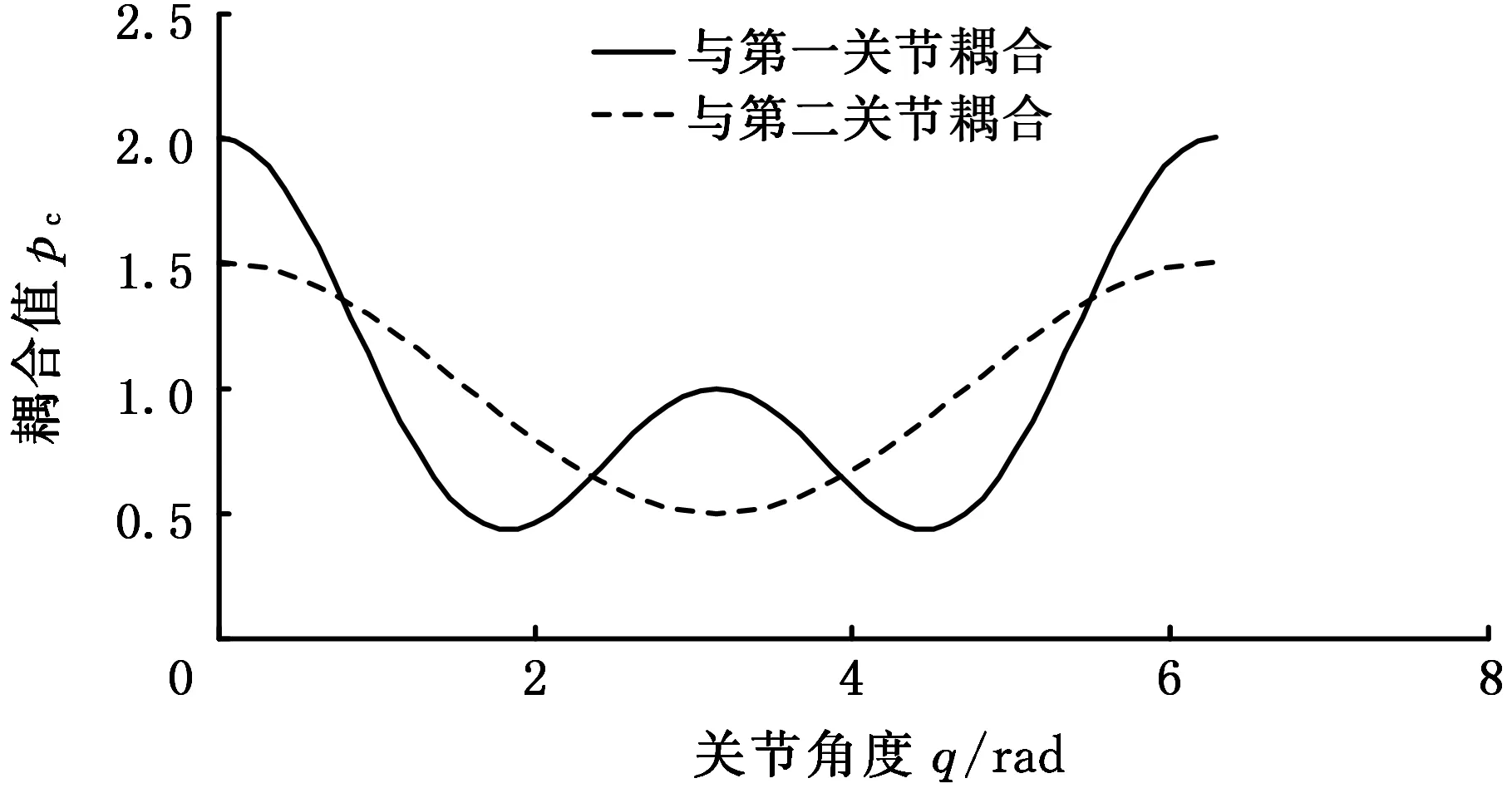
圖9 速度為0時第三關節單關節耦合曲線Fig.9 Single joint coupling curve of the third joint at zero speed

關節最大值最小值平均值方差12．0050．4361．0160．51521．5030．4971．0080．358

從運動耦合角度分析，最大耦合值表示在一定位姿時主動關節的角加速度對自由關節的角加速度的影響最大，自由關節最容易被驅動;最小耦合值表示在一定的位姿時主動關節的角加速度對自由關節的影響最小，自由關節最不容易被驅動。

圖9直觀地表達了單關節耦合指數變化趨勢。關節角度在0、π、2π附近區間，與第一關節的耦合值較大，其他區間與第二關節的耦合值較大。在耦合值較大的區域內，選擇此主動關節驅動自由關節，可增加整個欠驅動機械臂的運行效率，同時可有效節省能量。由此，單關節耦合指標分析結果可作為欠驅動機械臂控制策略的指導。

與上述相同條件下，圖10、表5分別為第一、第二關節轉動速度為15 rad/s時，第三關節的單關節耦合曲線及耦合參數。

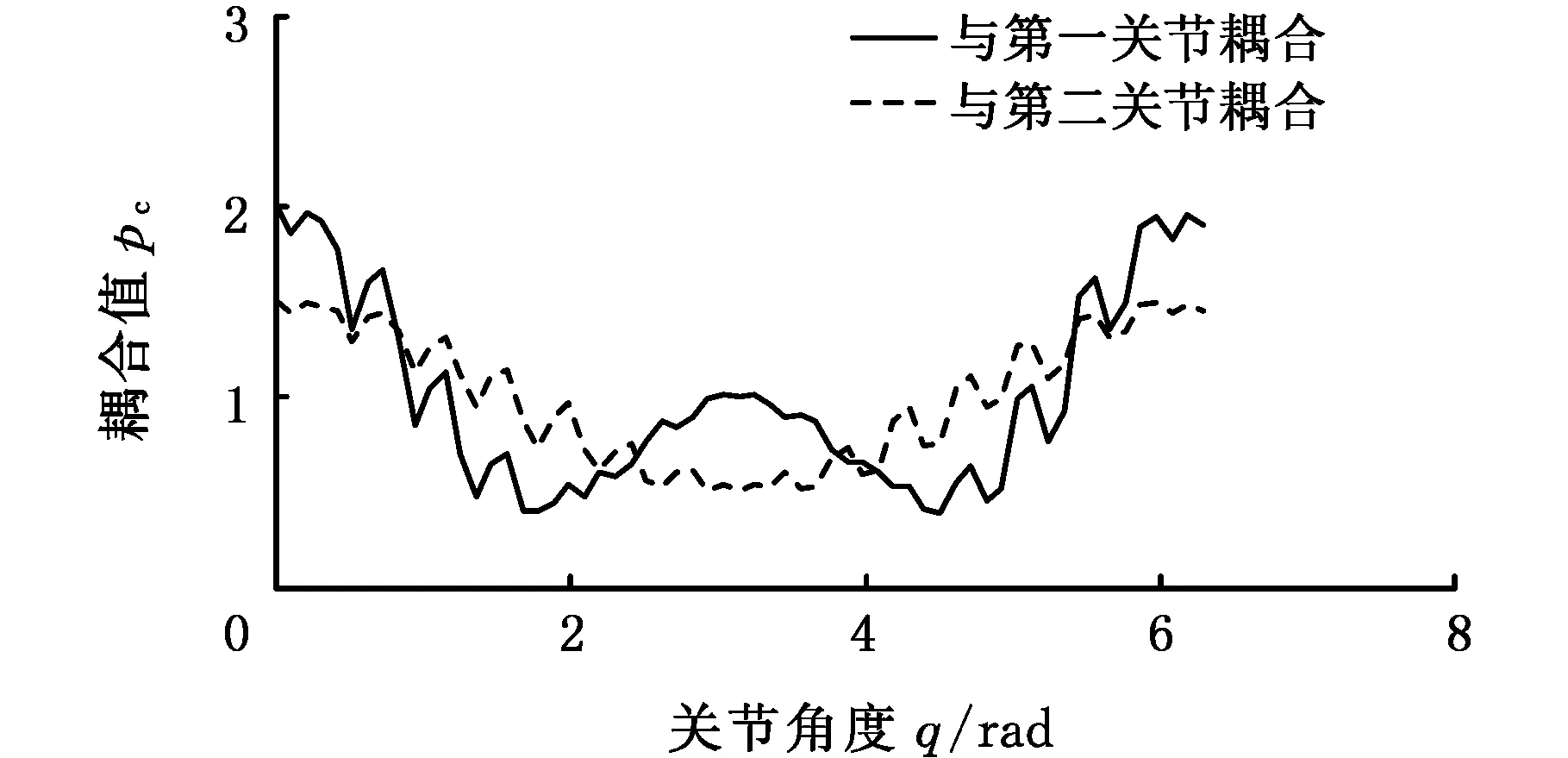
圖10 速度為15 rad/s時第三關節單關節耦合曲線Fig.10 Single joint coupling curve of the third joint at 15 rad/s speed 表5 速度為15 rad/s時第三關節單關節耦合參數

關節最大值最小值平均值方差12．0050．3911．0170．50421．5030．5081．0080．346

由圖9、圖10對比可知，當關節轉動速度為15 rad/s時，機械臂的彈性變形對耦合值影響明顯，但總體趨勢不變。表4、表5對應的耦合參數也相近。

3.2全局耦合指標對比分析

全局耦合指標用于分析關節運動空間內所有點的耦合關系：

(13)

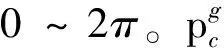
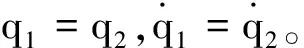
表6 速度為0時第三關節全局耦合參數

表7 速度為15 rad/s時第三關節全局耦合參數

由表6、表7對比可知，柔性機械臂的彈性變形對自由關節的全局耦合指數影響很小。在整個運動空間條件下，第三關節與第一關節的耦合值大于第三關節與第二關節的耦合值，這與表4、表5結果相符。由此證明全局耦合指標的合理性。

由以上分析結果可知，柔性欠驅動機械臂相對于剛性欠驅動機械臂，關節耦合參數相近。對于柔性欠驅動機械臂，主要問題在于運動過程中的彈性變形，在實際運動過程中則表現為彈性振動。對柔性欠驅動機械臂運動控制的關鍵在于對其彈性振動的控制，因此柔性欠驅動機械臂的控制比剛性欠驅動機械臂的控制困難得多。

4 結論

對不同速度下的柔性欠驅動機械臂自由關節的耦合指數計算與仿真結果同時表明，添加了經迭代計算邊界條件的Euler-Bernoulli梁模型能更好地表現柔性機械臂彈性變形對耦合指數的影響。柔性欠驅動機械臂和剛性機械臂運動過程中，運動參數產生差異的原因在于柔性機械臂的彈性變形引起的關節耦合指數的變化。最后，對自由關節的單關節耦合指標和全局耦合指標進行計算，得到柔性機械臂的彈性變形對關節耦合指數的影響規律。柔性欠驅動機械臂相對于剛性欠驅動機械臂，具有更復雜的耦合特性，對柔性欠驅動機械臂的控制關鍵在于控制其彈性振動。

[1] 日本機器人學會.機器人科技:技術變革與未來圖景[M]. 許郁文, 曹茹蘋, 蔣智揚,等譯.北京：人民郵電出版社, 2015: 1-40.

Japan Robot Association. Japanese Robotics Society: Technological Change and the Future Picture [M]. XU Yuwen, CAO Ruping, JIANG Zhiyang, et al trans. Beijing:People’s Posts and Telecommunications Press, 2015: 1-40.

[2] DEIMEL R, BROCK O. A Novel Type of Compliant and Underactuated Robotic Hand for Dexterous Grasping[J]. International Journal of Robotics Research, 2015, 35(1):161-185.

[3] 陳懇, 付成龍. 仿人機器人理論與技術[M]. 北京：清華大學出版社, 2010: 1-30.

CHEN Ken, FU Chenglong. Theory and Technology of Humanoid Robot[M]. Beijing:Tsinghua University Press, 2010: 1-30.

[4] 何廣平, 陸震, 王鳳翔,等. 柔性欠驅動機械臂的內共振現象及應用[J]. 北京航空航天大學學報, 2005, 31(8):913-916.

HE Guangping, LU Zhen, WANG Fengxiang, et al. Internal Resonance Property of Flexible Under-actuated Manipulators[J]. Journal of Beihang University, 2005, 31(8):913-916.

[5] 陳煒, 余躍慶, 張緒平,等. 欠驅動柔性機器人動力學建模及仿真[J]. 中國機械工程, 2006, 17(9):931-936.

CHEN Wei, YU Yueqing, ZHANG Xuping, et al. Dynamic Modeling and Simulation of Underactuated Flexible Robot [J]. China Mechanical Engineering, 2006, 17(9):931-936.

[6] 方建士, 章定國. 旋轉懸臂梁的剛柔耦合動力學建模與頻率分析[J]. 計算力學學報, 2012, 29(3):333-339.

FANG Jianshi, ZHANG Dingguo. Rigid-flexible Coupling Dynamic Modeling and Frequency Analysis of a Rotating Cantilever Beam[J]. Chinese Journal of Computational Mechanics, 2012, 29(3):333-339.

[7] 陳思佳. 剛-柔耦合問題與空間多桿柔性機械臂的動力學建模理論研究[D]. 南京：南京理工大學, 2012.

CHEN Sijia. Researches on the Rigid-Flexible Coupling Problem and the Dynamic Modeling Theory of Multi-link Spatial Flexible Manipulator Arms[D]. Nanjing:Nanjing University of Science and Technology. 2012.

[8] 范紀華, 章定國. 基于變形場不同離散方法的柔性機器人動力學建模與仿真[J]. 力學學報, 2016, 48(4): 843-856.

FAN Jihua, ZHANG Dingguo. Dynamic Modeling and Simulation of Flexible Robot Based on Different Discretization Methods[J]. Journal of Mechanics, 2016, 48(4): 843-856.

[9] 楊輝. 剛-柔耦合動力學系統的建模理論與實驗研究[D]. 上海：上海交通大學, 2002.

YANG Hui. Study on Dynamic Modeling Theory and Experiments for Rigid-Flexible Coupling Systems[D]. Shanghai: Shanghai Jiao Tong University, 2002.

[10] BERGERMAN M, LEE C, XU Y. Dynamic Coupling of Underactuated Manipulators[C]// Proceedings of the 4th IEEE Conference on Control Applications. Albany, 1995:500-505.

[11] RAO S S, 著.機械振動[M].李欣業, 張明路, 譯.4版.北京：清華大學出版社, 2009：431-446.

RAO S S. Mechanical Vibration[M]. LI Xinye, ZHANG Minglu, trans. 4th ed. Beijing: Tsinghua University Press, 2009:431-446.

[12] BERGERMAN M, LEE C, XU Y. A Dynamic Coupling Index for Underactuated Manipulators[J]. Journal of Robotic Systems, 1995, 12(10):693-707.

[13] GOSSELINC M, ANGELES J. A Global Performance Index for the Kinematic Optimization of Robotic Manipulators[J]. Journal of Mechanical Design, 1991, 113(3):220-226.

(編輯王旻玥)

DynamicsCouplingAnalysisofFlexibleUnderactuatedManipulators

LIU Jianying WANG Xiaoyue GONG Jinliang

School of Mechanical Engineering,Shandong University of Technology,Zibo,Shandong,255049

To establish flexible 3R underactuated manipulator dynamics equations, Euler-Bernoulli beam model was used with boundary conditions of iterative computations, the flexible robotic arm was coupled with the dynamics simulation. Based on the flexible manipulator modal analyses, the flexible manipulator was regarded as cantilever arm and simply supported free beam model with boundary conditions. A dynamics model of flexible 3R underactuated manipulators was established by assumed mode method. Simulation results show that the addition of boundary conditions for the iterative calculations of the flexible beam model may get a better reflection of the coupling accelerations of freedom joints. Finally, the coupling underactuated indices of flexible and rigid underactuated manipulators were analyzed. The results reveal that the flexible manipulator joints contain more complex coupling situations. The key to control underactuated flexible manipulators is to control the elastic vibrations of flexible manipulators.

underactuated; flexible manipulator; elastic deformation; coupling analysis

TP24

10.3969/j.issn.1004-132X.2017.22.013

2016-09-28

國家自然科學基金資助項目(61303006)；山東省優秀中青年科學家科研獎勵基金資助項目(BS2012ZZ009)