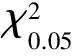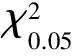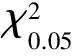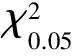全樣本場合下兩參數Birnbaum-Saunders疲勞壽命分布的統計分析
徐曉嶺,王蓉華,顧蓓青*
(1. 上海對外經貿大學 統計與信息學院,上海 201620; 2. 上海師范大學 數理學院,上海 200234)
全樣本場合下兩參數Birnbaum-Saunders疲勞壽命分布的統計分析
徐曉嶺1,王蓉華2,顧蓓青1*
(1. 上海對外經貿大學 統計與信息學院,上海 201620; 2. 上海師范大學 數理學院,上海 200234)
通過對數變換給出了求兩參數Birnbaum-Saunders(BS)疲勞壽命分布BS(α,β)在全樣本場合下參數的對數矩估計,并通過大量Monte-Carlo模擬比較了各種點估計方法的精度.基于對數變換通過一階泰勒展開,將兩參數BS疲勞壽命分布BS(α,β)近似看作兩參數對數正態分布,由此得到了2個參數α,β的近似區間估計,通過Monte-Carlo模擬發現,所給出的近似方法比原有方法更精確.最后通過若干實例說明了方法的可行性.
兩參數Birnbaum-Saunders疲勞壽命分布;形狀參數;刻度參數;點估計;近似區間估計
Birnbaum-Saunders疲勞壽命分布是概率物理方法中的一個重要失效模型,該模型是BIRNBANUM和SAUDERS[1]于1969年在研究主因裂紋擴展導致材料失效過程中推導而來,主要應用于疲勞失效研究,它比常用壽命分布如Weibull分布等更適合描述某些由疲勞引起失效的產品壽命失效規律.
設T服從兩參數Birnbaum-Saunders疲勞壽命分布BS(α,β),其分布函數與密度函數分別為:
其中,α>0為形狀參數,β>0為刻度參數(或者稱為尺度參數),φ(x),Φ(x)分別為標準正態分布的密度函數與分布函數,即

關于兩參數Birnbaum-Saunders疲勞壽命分布BS(α,β)的統計分析方法已有眾多研究[1-29].需要指出的是,2014年BALAKRISHNAN等[28]證明了在定數截尾和定時截尾下兩參數BS分布參數的MLE存在且唯一,這一結果說明當形狀參數α>2時,文獻[4]關于似然函數有多個極值點這一看法是不正確的.關于兩參數BS分布刻度參數的區間估計通常采用文獻[19-20]所提出的2種方法,徐曉嶺等[29]通過Monte-Carlo模擬說明這2種方法可能無法得到參數β的區間估計.
論文通過對數變換給出了求兩參數BS疲勞壽命分布BS(α,β)在全樣本場合下參數的對數矩估計.基于對數變換通過一階泰勒展開,將兩參數BS疲勞壽命分布BS(α,β)近似看作兩參數對數正態分布,由此得到了2個參數α,β的近似區間估計,通過Monte-Carlo模擬發現,本文的近似方法比原有方法更精確.最后通過若干實例說明方法的可行性.
1 參數點估計的綜合比較分析
1.1方法1:參數點估計的新方法——對數矩估計
設T1,T2,…,Tn為來自Birnbaum-Saunders疲勞壽命分布總體T~BS(α,β)的一個容量為n的簡單隨機樣本,其樣本觀察值為t1,t2,…,tn.



若k為奇數時,E(Zk)=0;若k為偶數時,

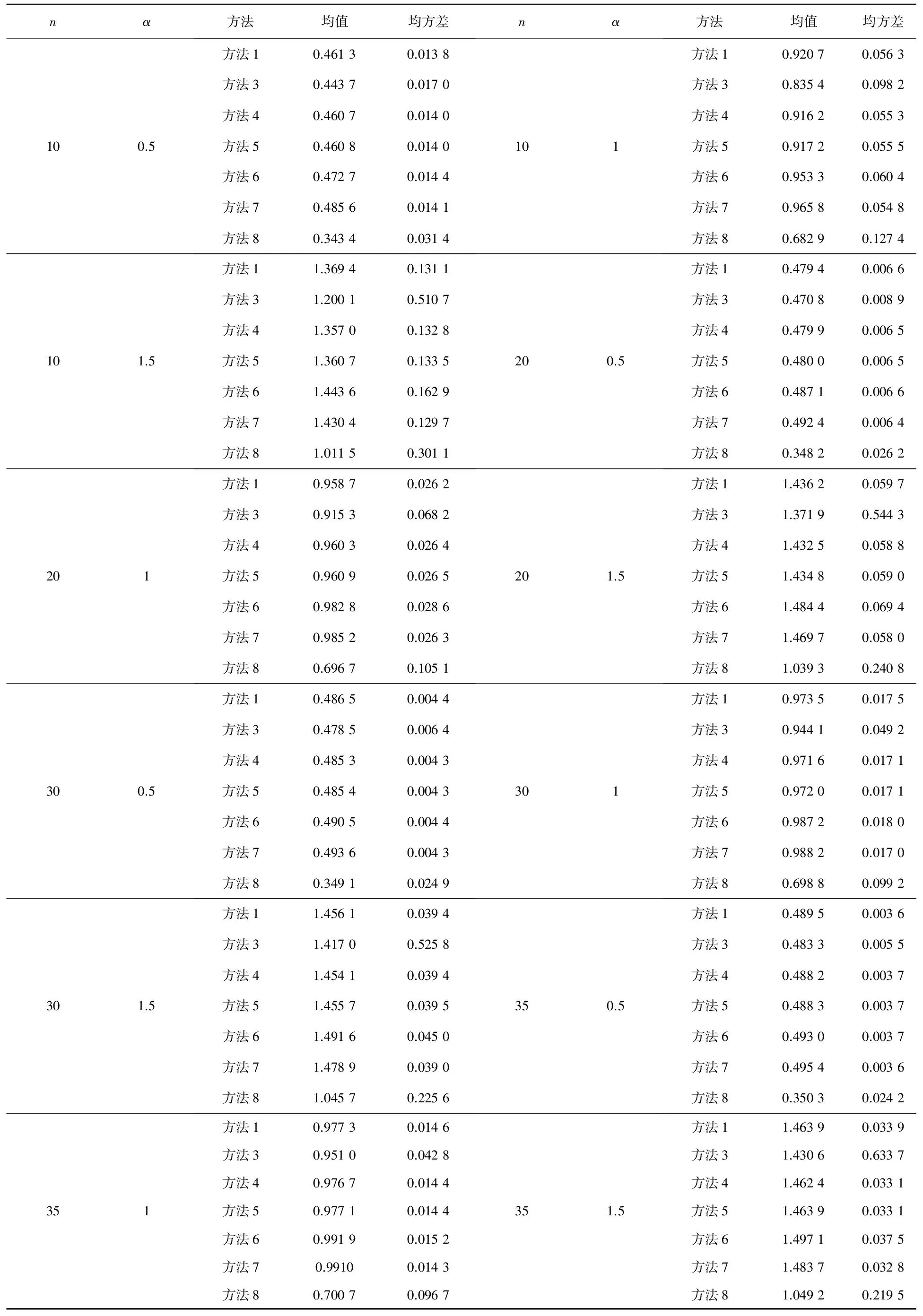
Y的分布函數FY(y)和密度函數fY(y)分別為: 對-∞ E(Y)=μ+2E(Z)=μ, E(Y2)=μ2+4E(Z2)= 引理1[30]設X1,X2,…,Xn是來自總體X的容量為n的一個簡單隨機樣本,記E(X)=μ,D(X)=σ2<+∞,該總體X的4階中心矩v4=E(X-EX)4有限,若函數h(x)的四階導數存在且有界,則有 證明Y=2Z+μ,E(Y)=μ,Y-E(Y)=2Z, 則Y的一至四階中心矩為: v1=E[Y-E(Y)]=0, v2=E[Y-E(Y)]2=4E(Z2)= v3=E[Y-E(Y)]3=8E(Z3)=0, v4=E[Y-E(Y)]4=16E(Z4)= 令函數h(x)=ex,h(x)的任意階導數任為ex,則 易證上述方程有唯一正實根. 1.2 方法2: 參數的極大似然估計[2, 14] 似然函數為: L(α,β)= 化簡得僅含參數β的超越方程: 需要指出的是,極大似然估計需要解非線性方程組,且計算較為復雜. 1.3 方法3: 矩估計 作簡單運算,可得BS(α,β)分布的如下特征. 引理2[14]設隨機變量T~BS(α,β),則 (1)T-1~BS(α,β-1); 化簡得僅含參數α的超越方程: 6α4+8α2+4=cα4+4cα2+4c, 即 (c-6)α4+4(c-2)α2+4(c-1)=0, Δ=16(c-2)2-16(c-6)(c-1)= 16(3c-2)>0, 又 (c-2)2-(3c-2)=c2-7c+6= (c-1)(c-6). 要使方法3的矩估計存在,則樣本數據應滿足: 1 表1 10 000次模擬中滿足c≥6的次數 Table 1 The number that satisfies c≥6 in 10 000 times of simulations 1.4 方法4: 矩估計 從中可解得參數β,α的矩估計分別為: 1.5 方法5: 逆矩估計 文獻[15]給出了參數的逆矩估計如下: 1.6 方法6: 分位數估計 設T1,T2,…,Tn為來自Birnbaum-Saunders疲勞壽命分布總體T~BS(α,β)的一個容量為n的簡單隨機樣本,其次序統計量記為T(1)≤T(2)≤…≤T(n). 進而參數α的點估計可取為 1.7 方法7: 回歸估計 文獻[21]利用回歸分析模型,給出了如下參數的最小二乘估計: 1.8 方法8: 回歸估計 由于 則 進而, 1.9 方法9: 回歸估計 由于 1.10 參數點估計的模擬及比較分析 比較上述9種點估計方法,方法2由于涉及復雜的超越方程求解,在此不推薦使用. 下面通過10 000次Monte-Carlo模擬比較方法1、方法3~方法9的β點估計的精度.給定樣本容量n=10,20,30,35,參數α=0.5,1,1.5,β=1,通過10 000次模擬得參數β的估計均值與均方差(其中方法3都滿足1 (1) 固定n,隨著α的增大,參數β估計的均值與真值的偏差增大,均方誤差也增大; (2) 固定參數α的真值,參數β的估計隨著n的增加變精確; (3) 方法1,4,5中參數β估計的無偏性較為明顯,同時其均方誤差也較小,相對而言,方法4的均方誤差更小,方法5與方法1均方誤差很接近. 下面通過10 000次Monte-Carlo模擬,比較方法1、方法3~方法8(方法9與方法8同)的α點估計的精度.給定樣本容量n=10,20,30,35,參數α=0.5,1,1.5,β=1,通過10 000次模擬得參數α的估計均值與均方差(其中方法3都滿足1 (1) 固定α,隨著n的增大,參數α估計的均方誤差在減少,即估計變精確; (2) 方法1、方法4~方法7的均方誤差相差不大,考慮到其均值,使用方法6或方法7更合理. 首先,給出利用對數正態分布求參數的區間估計方法(記為方法2),進而通過Monte-Carlo模擬與文獻[20-21]的方法(記為方法1)比較分析(在方法1能得到刻度參數β的區間估計的前提下). 記參數μ=lnβ,令Y=lnT,Yi=lnTi,i=1,2,…,n,則Y1,Y2,…,Yn為來自分布函數為 的一個容量為n的簡單隨機樣本,其次序觀察值記為y1,y2,…,yn. 表2 方法1、方法3~方法9參數β估計的Monte-Carlo模擬比較 Table 2 Comparisons on estimation methods 1, 3, 4,…, 9 of parameter β by Monte-Carlo simulations 表3 參數α估計方法的Monte-Carlo模擬比較 Table 3 Comparisons on estimation methods of parameter α by Monte-Carlo simulations 此時, 進而參數β的置信水平1-γ的近似區間估計為 參數α的置信水平1-γ的近似區間估計為 下面通過10 000次Monte-Carlo模擬,比較方法1、方法2關于參數α,β的區間估計的優劣.給定樣本容量n=5,10,15,參數α=0.5,1,1.5,β=1,置信水平1-γ=0.90,通過10 000次模擬(方法1中的參數β的區間估計都存在)得參數α,β區間估計的平均下限、平均上限、平均長度,以及區間估計包含參數真值的次數,結果列于表4.可知方法1、方法2所得的區間估計包含參數的真值次數都大于9 000;方法2所得的區間估計的平均長度較方法1要短.可知方法2比方法1更優. 表4 參數區間估計的模擬比較 Table 4 Simulation comparisons of interval estimations of parameters 表5 例1的參數點估計 Table 5 Point estimations of parameters in example 1 例1[14]數據來自BJERKEDAL(1960), 也被GUPTAETAL(1997)分析過.數據表示幾內亞豬注射不同劑量結核桿菌的生存時間.幾內亞豬對結核桿菌的敏感性比人類更高,首先關注在相同籠子里用相同養殖法養殖的豬.對于文中的養殖方法,有如下72個觀測值: 12,15,22,24,24,32,32,33,34,38,38,43,44,48,52,53,54,54,55,56,57,58,58,59,60,60,60,60,61,62,63,65,65,67,68,70,70,72,73,75,76,76,81,83,84,85,87,91,95,96,98,99,109,110,121,127,129,131,143,146,146,175,175,211,233,258,258,263,297,341,341,376. 經計算得:c=1.651 2,d=0.063 1. 取置信水平為0.90, 利用區間估計方法1、方法2得參數β,α的置信水平為0.90的區間估計,如表6如示. 表6 例1的參數區間估計 Table 6 Interval estimations of parameters in example 1 例2[7]本實例中的數據集為6061-T6鋁合金的疲勞壽命.鋁合金的切取位置應平行于軋制方向,振蕩頻率為18 Hz.該數據集包括101個觀測值,最大應力為31 000 Pa.數據如下: 70, 90, 96, 97, 99,100,103,104,104,105,107,108,108,108,109,109,112,112,113,114,114,114,116,119,120,120,120,121,121,123,124,124,124,124,124,128,128,129,129,130,130,130,131,131,131,131,131,132,132,132,133,134,134,134,134,134,136,136,137,138,138,138,139,139,141,141,142,142,142,142,142,142,144,144,145,146,148,148,149,151,151,152,155,156,157,157,157,157,158,159,162,163,163,164,166,166,168,170,174,196,212. 經計算得:c=1.027 7,d=0.003 6. 表7 例2的參數點估計 Table 7 Point estimations of parameters in example 2 表8 文獻[7]中參數的其他幾種點估計 Table 8 Other point estimations of parameters in reference[7] 文獻[7]還給出了其他幾種估計: 取置信水平為0.90, 取置信水平為0.95, 利用區間估計方法1、方法2得參數β,α的置信水平為0.90,0.95時的區間估計,如表9如示. 表9 例2的參數區間估計 Table 9 Interval estimations of parameters in example 2 例3[31]對于空氣污染物濃度,假定數據不相關且相互獨立,因此,一晝夜或循環趨勢分析是無必要的.這一假設得到了很多學者(包括GOKHALE和KHARE等)的支持.例如,環境數據有時以均值作為指標,因此空間-時間依賴性不復存在.以下數據對應的是1973年5~9月紐約每日的臭氧濃度(由紐約州環境保護部提供): 41,36, 12,18,28,23,19, 8, 7,16,11,14,18,14,34,6,30,1,11,4,32,23,45,115,37,29,71,39,23,21,37,20,12,13,49,32,64,40,77,97,97,85,10, 27,7,48,35,61,79,63,16,108,20,52,82,50,64,59,39,9,16,78,35,66,122,89,110,44,65,22,59,23,31,44,21,9,45,168,73,76,118,84,85, 96,78,91,47,32,20,23,21,24,44,21,28,9,13,46,18,13,24,16,23, 36,7,14,30,14,18,20,11,135,80,28,73,13. 表10 例3的參數點估計 Table 10 Point estimations of parameters in example 3 經計算得:c=1.607 8,d=0.092 8. 取置信水平為0.90, 利用區間估計方法1、方法2得參數β,α的置信水平為0.90時的區間估計,如表11如示. 表11 例3的參數區間估計 Table 11 Interval estimations of parameters in example 3 例4[32](1) 第1個實例是有關洪水峰值的超過數,含1958~1984年共72個超過數,四舍五入到小數點后1位,數據如下: 1.7,2.2,14.4,1.1,0.4,20.6,5.3,0.7,1.9,13.0,12.0,9.3,1.4,18.7,8.5,25.5,11.6,14.1,22.1,1.1,2.5,14.4,1.7,37.6,0.6,2.2,39.0,0.3,15.0,11.0,7.3,22.9,1.7,0.1,1.1,0.6,9.0,1.7,7.0,20.1,0.4,2.8,14.1,9.9,10.4,10.7,30.0,3.6,5.6,30.8,13.3,4.2,25.5,3.4,11.9,21.5,27.6,36.4,2.7,64.0,1.5,2.5,27.4,1.0,27.1,20.2,16.8,5.3,9.7,27.5,2.5,27.0. 經計算得:c=2.001 2,d=0.247 5. 表12 例4第1個實例的參數點估計 Table 12 Point estimations of parameters in the first case of example 4 取置信水平為0.90, 利用區間估計的方法1、方法2得參數β,α的置信水平為0.90時的區間估計,如表13如示. 表13 例4第1個實例的參數區間估計 Table 13 Interval estimations of parameters in the first case of example 4 (2) 第2個實例是有關50個工業設備的使用期,時間為零時進行壽命測試,數據如下: 0.1,0.2,1,1,1,1,1,2,3,6,7,11,12,18,18,18,18,18,21,32,36,40,45,46,47,50,55,60,63,63,67,67,67,67,72,75,79,82,82,83,84,84,84,85,85,85,85,85,86,86. 經計算得:c=1.506 2,d=0.382. 取置信水平為0.90, 利用區間估計方法1、方法2得參數β,α的置信水平為0.90時的區間估計,如表15如示. 表14 例4第2個實例的參數點估計 Table 14 Point estimations of parameters in the second case of example 4 表15 例4第2個實例的參數區間估計 Table 15 Interval estimations of parameters in the second case of example 4 [1] BIRNBAUM Z W, SAUNDERS S C. A new family of life distribution[J].JournalofAppliedProbability, 1969, 6(2): 319-327. [2] DESMOND A F. Stochastic models of failure in random environments[J].CanadianJournalofStatistics, 1985, 13(3): 171-183. [3] DESMOND A F. On the relationship between two fatigue-life models[J].IEEETransactionsonReliability, 1986, 35(2): 167-169. [4] BIRNBAUM Z W, SAUNDERS S C. Estimation for a family of life distributions with applications to fatigue[J].JournalofAppliedProbability, 1969, 6(2): 328-347. [5] ENGELHARDT M, BAIN L J, WRIGHT F T. Inferences on the parameters of the Birnbaum Saunders fatigue life distribution based on maximum likelihood estimation[J].Technometrics, 1981, 23(3): 251-256. [6] RIECK J R, NEDELMAN J R. A log-linear model for the Birnbaum Saunders distribution[J].Techanometrics, 1991, 33(1): 51-60. [7] NG H K T, KUNDU D, BALAKRISHNAN N. Modified moment estimation for the two-parameter Birnbaum-Saunders distribution[J].ComputationalStatisticsandDataAnalysis, 2003, 43(3): 283-298. [8] DUPUIS D J, MILLS J E. Robust estimation of the Birnbaum-Saunders distribution[J].IEEETransactionsonReliability, 1998, 47(1): 88-95. [9] CHANG D S, TANG L C. Reliability bounds and critical time for the Birnbaum-Saunders distribution[J].IEEETransactionsonReliability, 1993, 42(3): 464-469. [10] RIECK J R. Parametric estimation for the Birnbaum-Saunders distribution based on symmetrically censored samples[J].CommunicationinStatistics-TheoryandMethods, 1995, 24(7): 1721-1736. [11] OWEN W J, PADGETT W J. A Birnbaum-Saunders accelerated life model[J].IEEETransactionsonReliability, 2000, 49(2): 224-229. [12] OWEN W J, PADGETT W J. Acceleration models for system strength based on Birnbaum-Saunders distribution[J].LifetimeDataAnalysis, 1999, 5(2): 133-147. [13] OWEN W J, PADGETT W J. Power-law accelerated Birnbaum-Saunders life models[J].InternationalJournalofReliabilityQualityandSafetyEngineering, 2000, 7(7): 1-15. [14] KUNDU D, KANNAN N, BALAKRISHNAN N. On the hazard function of Birnbaum-Saunders distribution and associated inference[J].ComputationalStatistics&DataAnalysis, 2008, 52(5): 2692-2702. [15] 王炳興,王玲玲. Birnbaum-Saunders疲勞壽命分布的參數估計[J].華東師范大學學報:自然科學版, 1996(4): 10-15. WANG B X, WANG L L. Parameter estimation of Birnbaum-Saunders fatigue life distribution[J].JournalofEastChinaNormalUniversity:NaturalSciences, 1996(4): 10-15. [16] 王炳興,王玲玲. Birnbaum-Saunders疲勞壽命分布在截尾試驗情形的統計分析[J].應用概率統計, 1996, 12(4): 369-375. WANG B X, WANG L L. Statistical analysis of Birnbaum-Saunders fatigue life distribution in the censored test case[J].AppliedProbabilityandStatistics, 1996, 12(4): 369-375. [17] 王蓉華,費鶴良. 雙邊截尾場合下BS疲勞壽命分布的參數估計[J].上海師范大學學報:自然科學版, 1999, 28(2): 17-22. WANG R H, FEI H L. Parameter estimation for the BS fatigue life distribution under bilateral censoring[J].JournalofShanghaiNormalUniversity:NaturalSciences, 1999, 28(2): 17-22. [18] WANG R H, FEI H L. Statistical analysis for the Birnbaum-Saunders fatigue life distribution under multiply type II censoring[J].ChineseQuarterlyJournalofMathematics, 2006, 21(1): 15-27. [19] WANG R H, FEI H L. Statistical analysis for the Birnbaum-Saunders fatigue life distribution under type II bilateral censoring and multiply type II censoring[J].ChineseQuarterlyJournalofMathematics, 2004, 19(2): 126-132. [20] 孫祝嶺. Birnbaum-Saunders疲勞壽命分布尺度參數的區間估計[J].兵工學報, 2009, 30(11): 1558-1561. SUN Z L. Interval estimation of scale parameter for Birnbaum-Saunders fatigue life distribution[J].ActaArmamentarii, 2009, 30(11): 1558-1561. [21] 孫祝嶺. Birnbaum-Saunders 疲勞壽命分布參數的回歸估計方法[J].兵工學報, 2010, 31(9): 1260-1262. SUN Z L. Regression estimation method of parameters for Birnbaum-Saunders fatigue life distribution[J].ActaArmamentarii, 2010, 31(9): 1260-1262. [22] 孫祝嶺. 疲勞壽命分布變異系數的統計推斷[J].質量與可靠性, 2013(1): 13-15. SUN Z L. Statistical inference of variable coefficient for fatigue life distribution[J].QualityandReliability, 2013(1): 13-15. [23] 孫祝嶺. Birnbaum-Saunders分布環境因子的置信限[J].強度與環境, 2012, 39(4): 51-55. SUN Z L. Confidence limit of environmental factor for Birnbaum-Saunders distribution[J].Structure&EnvironmentEngineering, 2012, 39(4): 51-55. [24] WANG B X. Generalized interval estimation for the Birnbaum-Saunders distribution[J].ComputationalStatisticsandDataAnalysis, 2012, 56(12): 4320-4326. [25] NIU C Z, GUO X, XU W L, et al. Comparison of several Birnbaum-Saunders distributions[J].JournalofStatisticalComputationandSimulation, 2014, 84(12): 2721-2733. [26] 周磊,孫玲玲. 一種基于概率解釋的新型互連線時延Slew模型[J].電路與系統學報, 2009, 14(2): 7-10. ZHOU L, SUN L L. A new slew interconnect delay model based on probability interpretation[J].JournalofCircuitsandSystems, 2009, 14(2): 7-10. [27] 趙建印,孫權,彭寶華,等. 基于加速退化數據的BS分布的統計推斷[J].電子產品可靠性與環境試驗, 2006, 24(1): 11-14. ZHAO J Y, SUN Q, PENG B H,et al. Statistical inference for BS distribution based on the accelerated degradation data[J].ElectronicProductReliabilityandEnvironmentalTest, 2006, 24(1): 11-14. [28] BALAKRISHNAN N, ZHU X J. On the existence and uniqueness of the maximum likelihood estimates of the parameters of Birnbaum-Saunders distribution based on type-I, type-II and hybrid censored samples[J].Statistics, 2014, 48(5): 1013-1032. [29] 徐曉嶺,王蓉華,顧蓓青. 關于兩參數Birnbaum-Saunders疲勞壽命分布統計分析的2個注記[J].浙江大學學報:理學版, 2016, 43(5): 539-544. XU X L, WANG R H, GU B Q. Two notes of statistical analysis about two-parameter Birnbaum-Saunders fatigue life distribution[J].JournalofZhejiangUniversity:ScienceEdition, 2016, 43(5): 539-544. [30] 徐曉嶺,王蓉華.概率論與數理統計[M]. 北京: 人民郵電出版社, 2014: 48-52, 174-178. XU X L, WANG R H.ProbabilityandMathematicalStatistics[M]. Beijing: Posts and Telecom Press, 2014: 48-52, 174-178. [31] VILCA F, SANTANA L, VICTOR LEIVA V, et al. Estimation of extreme percentiles in Birnbaum-Saunders distributions[J].ComputationalStatisticsandDataAnalysis, 2011, 55(4): 1665-1678. [32] CORDEIRO G M, LEMONTE A J. The exponentiated generalized Birnbaum-Saunders distribution[J].AppliedMathematicsandComputation, 2014, 247: 762-779. XU Xiaoling1, WANG Ronghua2, GU Beiqing1 (1.SchoolofStatisticsandInformation,ShanghaiUniversityofInternationalBusinessandEconomics,Shanghai201620,China; 2.MathematicsandScienceCollege,ShanghaiNormalUniversity,Shanghai200234,China) Statisticalanalysisoftwo-parameterBirnbaum-Saundersfatiguelifedistributionunderfullsample. Journal of Zhejiang University(Science Edition),2017,44(6): 692-704 The logarithmic moment estimations of parameters are proposed by logarithmic transformation for two-parameter Birnbaum-Saunders(BS) fatigue life distribution BS(α,β) under the full sample. The precisions of various point estimation methods are compared by a large number of Monte-Carlo simulations. Two-parameter BS fatigue life distribution BS(α,β) is approximately regarded as two-parameter lognormal distribution through the first order Taylor expansion based on logarithmic transformation. Then, the approximate interval estimations of two parametersα,βare obtained, and it can be found that this approximate method is more accurate than the original method by Monte-Carlo simulations. Finally, several examples show the feasibility of the methods. two-parameter Birnbaum-Saunders fatigue life distribution; shape parameter; scale parameter; point estimation; approximate interval estimation 2016-12-07. 國家自然科學基金資助項目 (11671264). 徐曉嶺(1965—),ORCID: http//orcid. org/0000-0002-9442-8555,男,博士,教授,主要從事應用統計研究,E-mail:xlxu@suibe.edu.cn. *通信作者: ORCID: http//orcid. org/0000-0003-1539-8747,E-mail:gubeiqing@suibe.edu.cn. 10.3785/j.issn.1008-9497.2017.06.008 O 213 A 1008-9497(2017)06-692-13

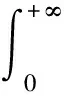
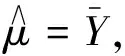
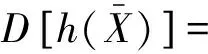


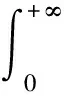
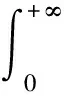
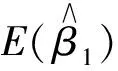
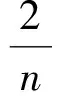
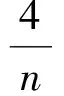



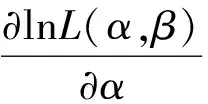



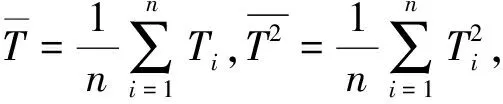





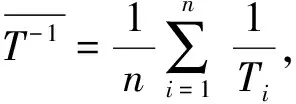



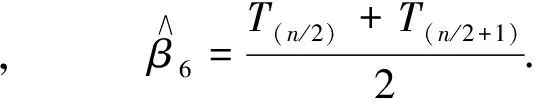
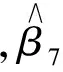
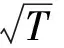

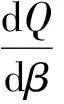
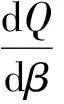
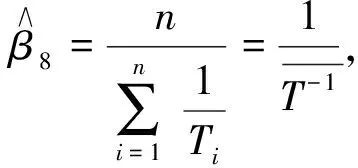

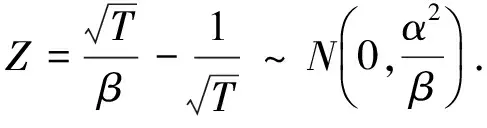
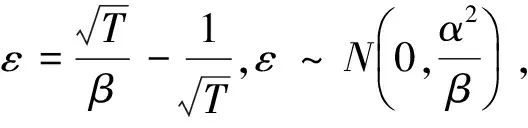
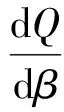
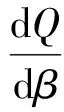



2 參數區間估計的比較分析
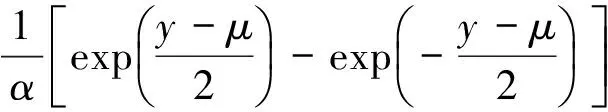


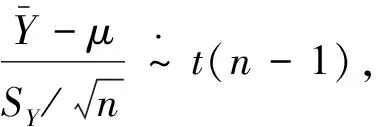



3 計算實例