剪切變形與轉動慣量對層合金屬厚壁短管振動模態的影響

郭建英， 白艷艷

(1. 太原理工大學 礦業工程學院，太原 030024； 2. 太原理工大學 機械工程學院，太原 030024)

剪切變形與轉動慣量對層合金屬厚壁短管振動模態的影響

郭建英1， 白艷艷2

(1. 太原理工大學 礦業工程學院，太原 030024； 2. 太原理工大學 機械工程學院，太原 030024)

對層合金屬厚壁短管進行振動分析必須考慮非勻質、剪切變形和轉動慣量效應。基于Timoshenko理論，推導了兩端簡支、兩端固支、兩端自由和懸臂四種邊界條件下，層合金屬厚壁短管彎曲振動的頻率函數與模態振型函數的表達式。采用計算機代數系統MAPLE對四種邊界條件下銅鋼層合厚壁短管的固有頻率進行求解，并繪制振型曲線。采用錘擊實驗法并結合有限元模態分析法，測得了銅鋼層合厚壁短管在兩端自由條件下彎曲振動的固有頻率。理論解與實測值相比的最大誤差為-4.56%，理論解與有限元解相比的最大誤差為-0.76%。求解了剪切變形與轉動慣量對銅鋼層合厚壁短管固有頻率的影響系數，并分析了該頻率影響系數與管子的振型曲線隨邊界條件、階序、層合管長徑比、以及壁厚比等參數的變化規律。

層合金屬厚壁短管；剪切變形；轉動慣量；頻率影響系數；模態振型

工業技術的發展對流體輸送與傳熱管件的高強度、抗腐蝕、耐磨損等綜合性能的要求逐漸提高，層合金屬管代替單一金屬管已成為發展趨勢和研究熱點[1-4]，并在石油、化工及核工業等領域得到廣泛應用[5-6]。管件在流體環境中極易發生流體誘導振動破壞，準確分析層合金屬管的彎曲振動特性，使其固有頻率遠離流體的漩渦脫落頻率或紊流抖振頻率，對預防和控制該結構的振動破壞有重要意義[7-9]。

層合金屬管屬于層合圓柱殼結構，國內外很多學者對該結構的振動特性進行了研究，如李驍等[10]建立了軸向運動層合圓柱殼體的橫向振動方程，分析了軸向速度、長徑比和厚徑比等對殼體振動特性的影響。張宇飛等[11]對軸向運動層合薄壁圓柱殼內共振特性進行了數值分析。Winfield等[12]采用梁模型對層合厚壁長錐形管的自由振動特性進行了研究。

由于圓柱殼沿軸向分布的彎曲振型接近于相應邊界條件下的梁振型函數[13]，因此分析細長薄壁層合金屬管的彎曲振動特性時，可以采用經典Euler-Bernoulli梁振動理論進行求解，并用截面組合剛度和等效質量加以反應其在厚度方向的非勻質特性[14]。但對于外徑與壁厚之比小于20，長度與直徑之比小于等于10的層合金屬厚壁短管，不但要考慮其非勻質特性、還應考慮剪切變形及轉動慣量的影響，即采用Timoshenko深梁振動理論對其彎曲振動特性進行分析。Timoshenko梁振動微分方程的特征值問題比較復雜，很難獲得振動頻率的顯式解析表達式，國內外的學者提出了多樣性指導演化算法、模態攝動法、歸一化波數法等[15-19]許多種解決方法，但這些方法如用于管子的工程振動設計則稍顯復雜。

本文擬推導出常用四種邊界條件下，Timoshenko梁振動頻率函數和振型函數的顯式表達式，利用計算機代數系統求解固有頻率并繪制振型曲線。確定剪切變形與轉動慣量對層合金屬厚壁短管的頻率影響系數，分析該頻率影響系數及管子振型曲線隨階序、長徑比、及管子非勻質參數的變化規律，為層合金屬厚壁短管的工程振動設計提供參考。

1 Timoshenko梁彎曲振動頻率函數和振型函數

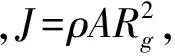
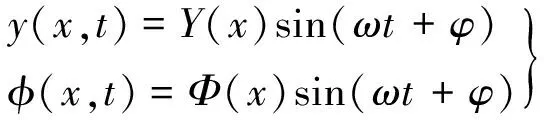
(1)

則考慮剪切變形和轉動慣量影響的Timoshenko梁振動微分方程的特征值問題為[20]

kGA[Φ′(x)-Y″(x)]-ω2ρAY(x)=0

(2)

kGA[Φ(x)-Y′(x)]-EIΦ″(x)-ω2JΦ(x)=0

(3)

其中，Y(x)和Φ(x)應滿足的邊界條件為

簡支端x=0或x=l，Y(x)=0，EIΦ′(x)=0

(4)

自由端x=0或x=l，EIΦ′(x)=0，kGA[Φ(x)-Y′(x)]=0

(5)

固支端x=0或x=l，Y(x)=0，Φ(x)=0

(6)

對等截面梁，由式(2)、(3)可得

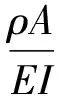
(7)

式中，Y″(x)系數中的兩項分別反映了剪切變形與轉動慣量的影響，而最后一項則反映了剪切變形與轉動慣量的耦合作用。

令梁振動的主模態函數為Y(x)=Cjerx，將其代入式(7)得

(8)

解該方程可得

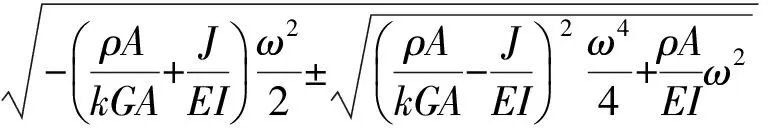
(i=1, 2, 3, 4)

(9)

這樣，梁振動的主模態函數為

ω<ωc時，Y(x)=C1sin(αx)+C2cos(αx)+

C3sinh(βx)+C4cosh(βx)

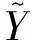
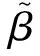
(10)

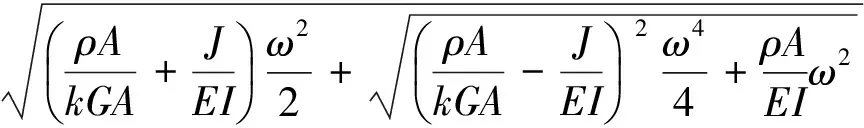
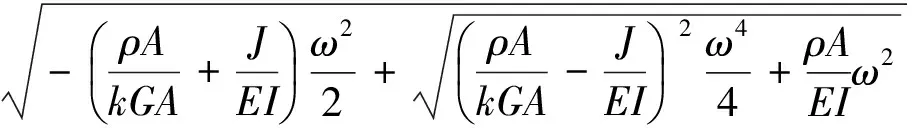
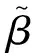
(11)

本文要確定截面剪切變形和轉動慣量的影響特性，獲得層合金屬厚壁短管固有頻率的簡捷計算公式。因此參考文獻[16]的方法，將式(11)中Timoshenko梁的固有圓頻率ωi表示為

ωi=λiωio，(i=1, 2, 3, …)

(12)

式中：λi為截面剪切變形和轉動慣量對結構固有頻率的影響系數，ωio為Euler-Bernoulli梁的固有圓頻率。

下面推導四種邊界條件下，Timoshenko梁振動頻率函數和振型函數的解析表達式。

1.1兩端簡支

將主模態函數式(10)代入兩端簡支邊界條件式(4)，可得Timoshenko梁的頻率方程為

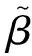
(13)

因此有

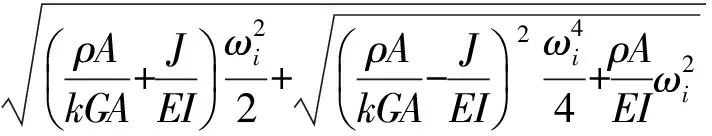
(14)

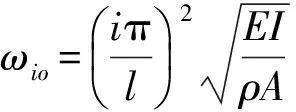
(15)

令方程(15)中的系數為

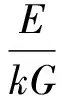
(16)

又已知0≤λi≤1，這樣方程(15)的解可表示為

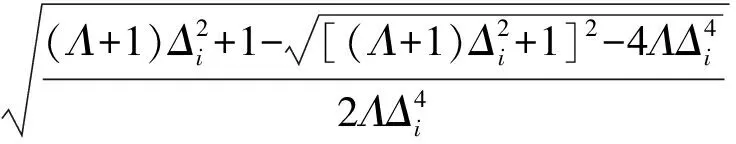
(17)

這樣，可得兩端簡支Timoshenko梁固有頻率的顯式計算公式為

(18)

式中：λi為頻率影響系數；Λ和Δi為計算系數，i為頻率階序。

兩端簡支時，可推導出Timoshenko梁彎曲振動的振型函數為

Y(x)=sin(iπx)，0≤x≤l

(19)

1.2兩端自由

由式(5)并結合式(2)和式(3)可得兩端自由Timoshenko梁的邊界條件為

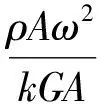
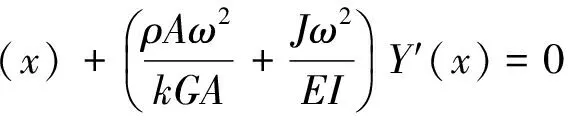
(20)

令式(20)中的計算參數為B1，B2，B3，其中

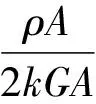
(21)

將式(21)代入式(11)和(20)，并將主模態函數式(10)代入式(20)，可推導出兩端自由時Timoshenko梁的頻率函數為

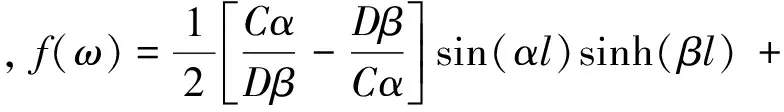
cos(αl)cosh(βl)-1

(22)

其中計算參數C，D分別為

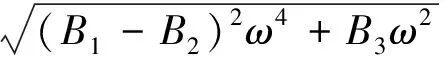
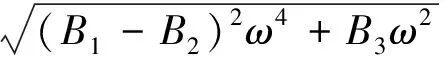
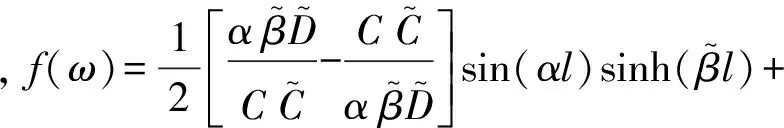
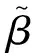
(23)

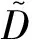
另外，由前面條件推導出兩端自由時Timoshenko梁的振型函數為

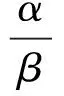
ξisinh(βx)+cosh(βx)

(24)

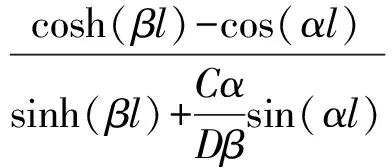
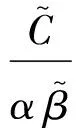
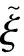
(25)

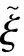
由于兩端固支、一端固支一端自由邊界條件時的推導過程與兩端自由類似，因此本文將這兩種邊界條件下Timoshenko梁的頻率函數與振型函數的結果列于表1中。

2 層合金屬厚壁短管非勻質特性

層合金屬管是由兩種不同金屬材料管沿壁厚疊合而成。圖1所示為銅鋼層合管，其結構材料參數見表2。

按照郭建英等對層合金屬管沿厚度方向的非勻質特性，可用截面組合剛度、等效組合質量、和等效轉動慣量加以反應。這樣，單位長度層合金屬厚壁短管的等效質量為

m=ρ1A1+ρ2A2

(26)

結構的截面組合彎曲剛度EI與截面組合剪切剛度kGA分別為

EI=E1I1+E2I2

(27)

kGA=k1G1A1+k2G2A2

(28)

式中，A1，A2，I1，I2分別為內層銅管和外層鋼管的截面積，及其截面對中性軸的慣性矩。k1、k2分別為內層銅管和外層鋼管的截面剪切修正系數，采用Cowper法[22]來確定

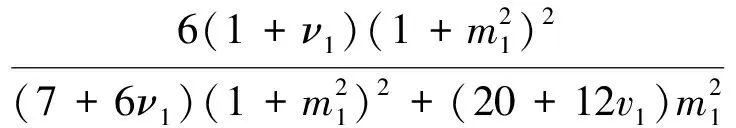
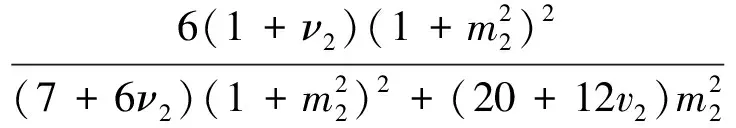
(29)

式中：ν1、ν2分別為內、外層管材料的泊松比；m1=D1/D2，m2=D2/D3分別為內、外層管的內外徑之比。

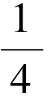
(30)

圖1 銅鋼層合管

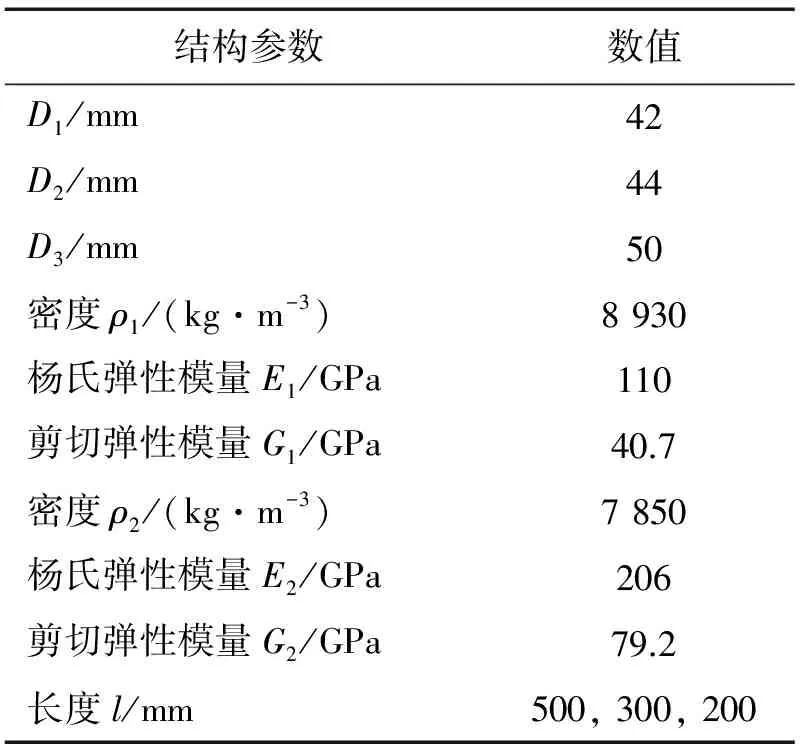
結構參數數值D1/mm42D2/mm44D3/mm50密度ρ1/(kg·m-3)8930楊氏彈性模量E1/GPa110剪切彈性模量G1/GPa40．7密度ρ2/(kg·m-3)7850楊氏彈性模量E2/GPa206剪切彈性模量G2/GPa79．2長度l/mm500，300，200

3 實驗測試與模態分析

為了驗證前面理論分析結果的準確性，本文用北京東方振動和噪聲技術研究所的INV3018A和DASP-V10振動信號采集分析系統，對銅鋼層合厚壁管(結構材料參數見表2)的固有頻率進行了實驗測試。實驗中，用兩條高彈性皮筋懸掛管子以實現兩端自由支撐。為了更準確的獲得各階頻率的測試值，沿管子軸線方向，在距離管子兩端各1/4處分別安裝兩個加速度傳感器，將兩個傳感器的實測頻譜圖對比之后獲得最終的實測結果。另外，沿管子軸線方向等間距設置10個測點，采用力錘對測點進行逐點敲擊。

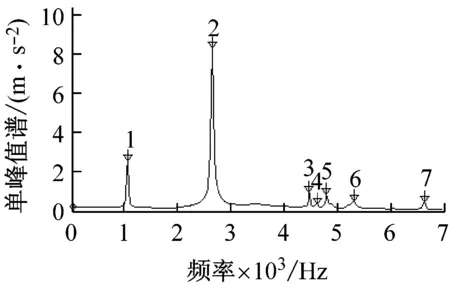
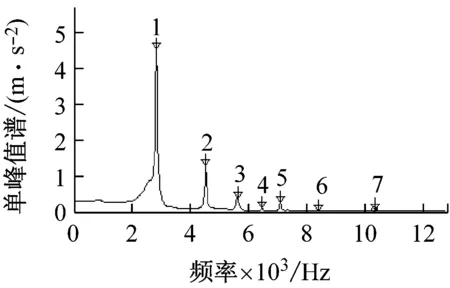
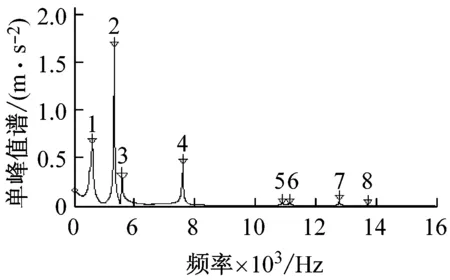
圖2(a)～圖2(c)分別顯示了兩端自由狀態下，不同長度銅鋼層合管固有頻率的實測自譜-FFT幅值譜圖。

由圓柱殼振動理論可知，直徑較大的管子在受到徑向沖擊力時，會產生橫向彎曲振動，也會產生周向振動。因此，實驗測到的管子振動特性應包括管子的橫向彎曲振動和周向振動兩種模態。由于管子在流體環境中主要發生的是橫向彎曲共振破壞，因此本文分析的是層合金屬厚壁短管的橫向彎曲振動頻率，這需要結合模態分析來識別圖2中管子的橫向彎曲振動頻率的數值。

本文用有限元軟件ANSYS對實測用的銅鋼層合管進行了模態分析。圖3顯示了長度為500 mm的管子在兩端自由時的前8階固有頻率和模態。

(a) l=500 mm

(b) l=300 mm

(c) l=200 mm

(a) f=1 059.2 Hz

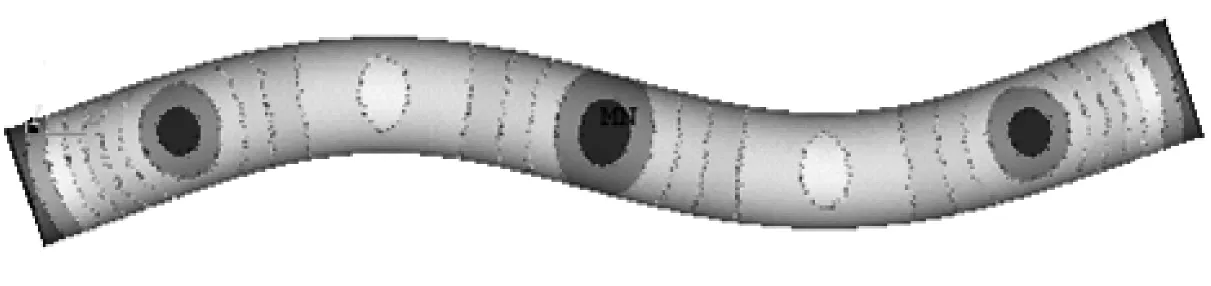
(b) f=2 667.0 Hz

(c) f=4 331.0 Hz

(d) f=4 506.4 Hz

(e) f=4 694.3 Hz

(f) f=4 878.3 Hz

(g) f=5 506.4 Hz

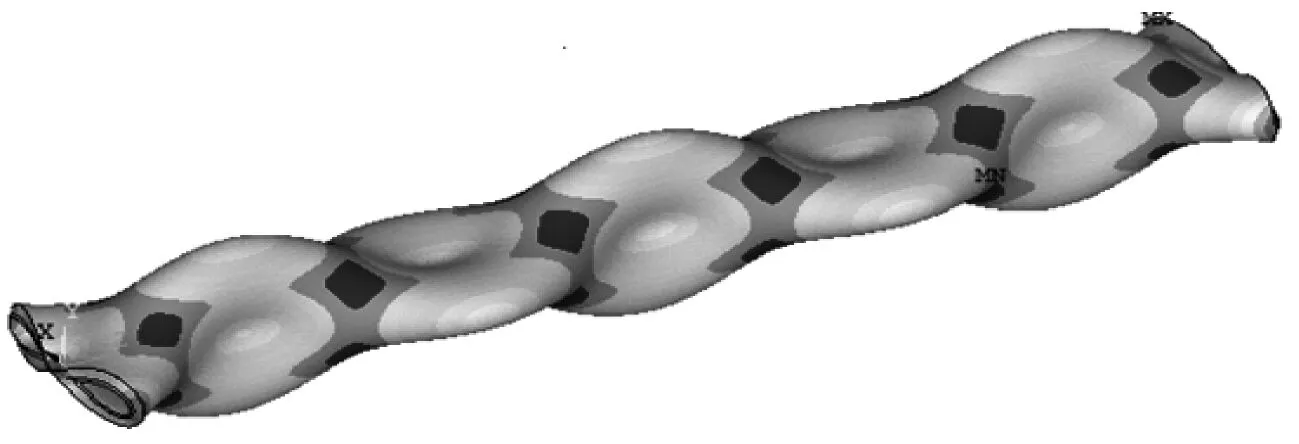
(h) f=6 394.7 Hz

比較圖2(a)與圖3(a)～圖3(h)可以發現，圖2(a)中實測的第1、2峰值對應的頻率1 072.1 Hz和2 673.1 Hz應為層合管的1、2階橫向彎曲振動固有頻率，模態振型如圖3(a)和圖3(b)所示；由于傳感器正好位于圖3(c)所示的1階周向模態振型的節點處，因此該特征值并未被檢測到；圖2(a)中實測第3峰值對應頻率4 510.8 Hz為層合管的2階周向振動模態特征值，模態振型如圖3(d)所示；實測的第4峰對應頻率值4 653.85 Hz為層合管的3階彎曲振動頻率，模態振型如圖3e所示；之后實測的第5、6、7峰值的頻率值4 830.5 Hz、5 342.6 Hz、6 655.1 Hz分別對應圖3(f)～圖3(h)中管子的3，4，5階周向振動模態特征值。采用同樣方法可以識別圖2(b)和圖2(c)中長度分別為300 mm和200 mm的層合管的橫向彎曲振動頻率。

4 結果與討論

4.1理論解、有限元解與實測值的比較

已知ωi=2πfi，fi為結構固有頻率，Hz。將該式代入頻率函數式(22)和(23)，利用計算機代數系統Maple編程繪制該頻率函數曲線，其與橫坐標軸的各交點即為兩端自由條件下層合管橫向彎曲振動的固有頻率值。圖4顯示了長度為500 mm的銅鋼層合管的頻率函數曲線及前三階固有頻率的數值。

表3列出了在兩端自由條件下，長度分別為500 mm、300 mm和200 mm的銅鋼層合管前3階彎曲振動固有頻率的理論解、有限元解和實測值及誤差。在表3中，誤差1為理論解與實測值相比的誤差，其最大值為-4.56%；誤差2為理論解與有限元解相比的誤差，其最大值僅為-0.76%。該結果表明上述理論方法可以對層合金屬厚壁短管的彎曲振動固有頻率和振型進行準確求解。誤差分析發現，誤差1主要來源于實測管件的加工不均勻。例如，長為300 mm的復合管，其實測重量為1.432 kg，而按照其結構參數計算得重量為1.405 kg，誤差為-1.92%；這種加工不均勻同時也會影響結構的剛度，最終使結構固有頻率的理論解與實測值存在偏差。

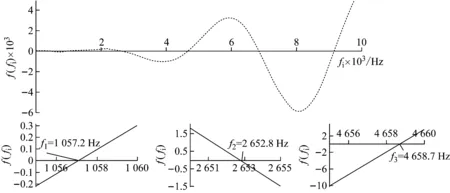
圖4 兩端自由時銅鋼層合管頻率函數曲線(l=500 mm)

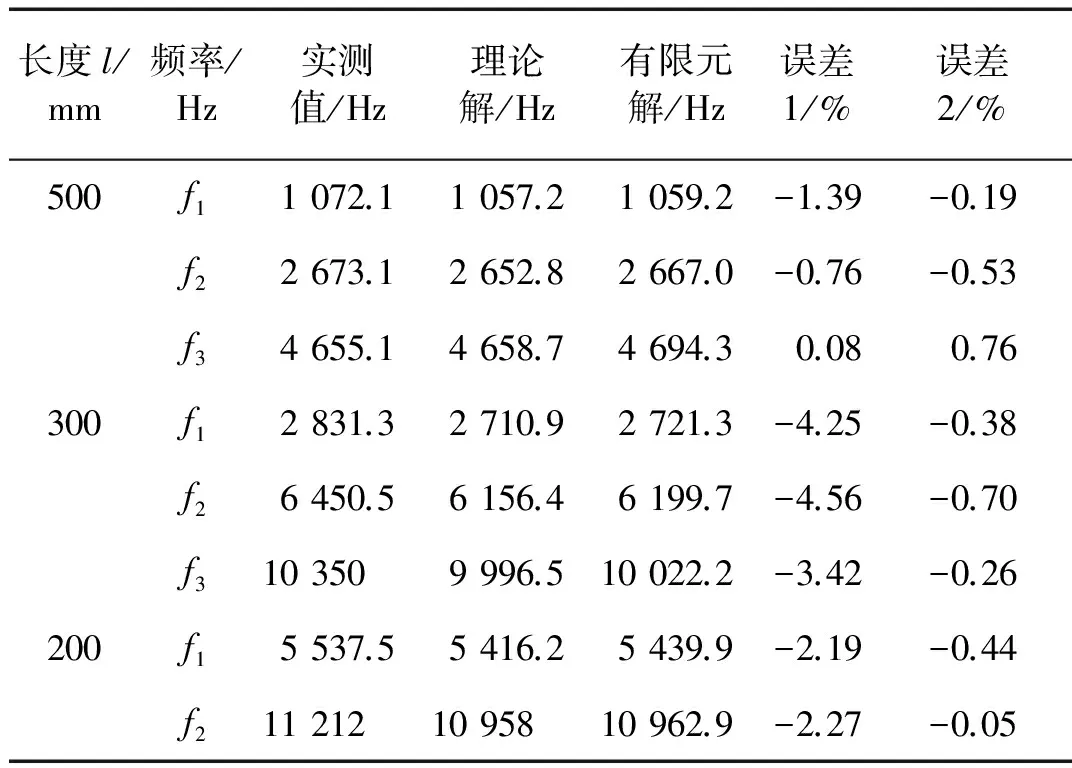
長度l/mm頻率/Hz實測值/Hz理論解/Hz有限元解/Hz誤差1/%誤差2/%500300200f11072．11057．21059．2-1．39-0．19f22673．12652．82667．0-0．76-0．53f34655．14658．74694．30．080．76f12831．32710．92721．3-4．25-0．38f26450．56156．46199．7-4．56-0．70f3103509996．510022．2-3．42-0．26f15537．55416．25439．9-2．19-0．44f2112121095810962．9-2．27-0．05

4.2頻率影響系數λi及其變化特性

由式(12)可知，將基于Timoshenko理論求解得層合管的固有頻率值與基于Euler-Bernoulli梁理論求解的固有頻率值相比，可獲得剪切變形和轉動慣量對管子固有頻率的影響系數λi。另由式(18)可知，頻率影響系數λi與階序i、層合管長徑比l/Rg、及其非勻質參數E/kG有直接關系，因此下面分析該頻率影響系數λi隨這些因素的變化特性。

4.2.1λi隨長徑比l/Rg、階序i、及邊界條件的變化

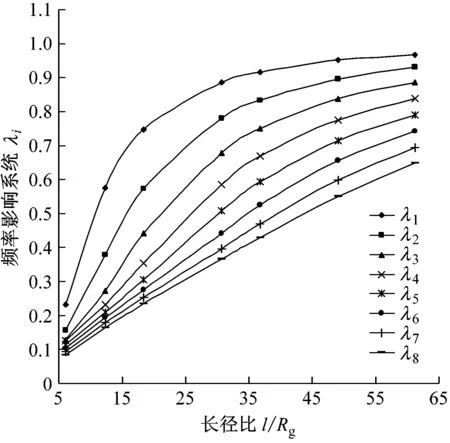
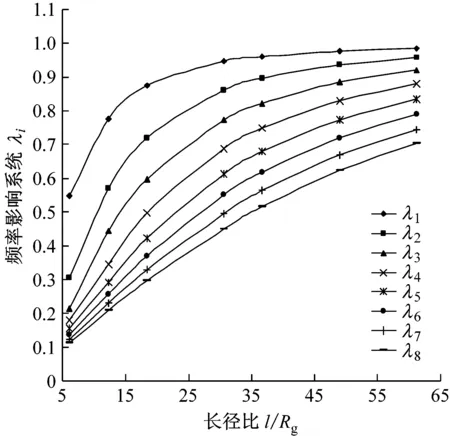
圖5顯示了四種邊界條件下，剪切變形與轉動慣量對銅鋼層合管固有頻率的影響系數λi隨長徑比和階序的變化規律。由圖5可知，剪切變形與轉動慣量會降低管子的固有頻率，這是由于轉動慣量會增加管子的慣性，而剪切變形會降低管子的剛度。另外，四種邊界條件下，頻率影響系數λi的數值均隨長徑比l/Rg的增大而增大，隨階序i的增大而減小；這表明結構的長徑比越小，剪切變形與轉動慣量對其固有頻率的影響越大，而且對高階頻率的影響尤為顯著。該結果與振動力學研究結論相符。

從圖5還可看出，邊界條件對λi有較大影響。例如，對工程振動設計中重點關注的1階頻率影響系數λ1而言：當結構長徑比l/Rg由6.125增到61.25時，兩端固支時λ1由0.232 3增大到0.967 5，見圖5(a)；兩端自由時λ1由0.548 8增大到0.985 8，見圖5(b)；兩端簡支時λ1由0.641 5增大到0.992 2，見圖5(c)；一端固支一端自由的頻率影響系數λ1由0.741 0增大到0.998 8，見圖5(d)。該結果表明，剪切變形與轉動慣量對層合管彎曲振動固有頻率的影響，在兩端固支時最大，兩端自由、兩端簡支次之，一端固支一端自由時的影響最小。這是由于邊界支撐條件對結構的系統剛度有較大影響，系統剛度的改變引起模態特征值的變化。

4.2.2λi隨層合管結構與材料組合的變化

層合金屬管的結構變化是指其內、外層管的不同壁厚組合，材料變化是指其內、外層管的不同材料組合。圖6(a)和圖6(b)分別顯示了兩端簡支條件下，銅鋼層合管和鋁鋼層合管的剪切變形與轉動慣量對其彎曲振動固有頻率的影響系數λi，隨其壁厚比n和階序i的變化特性。層合管的壁厚比n是指內層管壁厚與總管壁厚之比。

由圖6(a)可以看出，對于銅鋼層合管，當其壁厚比n由0.0(這時為純鋼管)增大到1.0(這時為純銅管)時，其前8階頻率影響系數λi(i=1～8)的均有微弱減小，但最大減小幅度僅為1.37%。由圖6(b)可以看出，對于鋁鋼層合管，當其壁厚比n由0.0(這時為純鋼管)增大到1.0(這時為純鋁管)時，其1階頻率影響系數λ1由0.970增大到0.980，增幅1.03%；而第8階頻率影響系數λ8則由0.475增大到0.545，增幅14.73%。

對上述結果分析發現，剪切變形與轉動慣量對復合管的頻率影響系數λi隨其結構與材料組合的變化特性，是由管子的非勻質無量綱參數E/kG引起的，該參數可表明層合管系統剛度的大小。如果層合管的系統剛度隨其壁厚比n的變化幅值較小，則其各階頻率影響系數λi的變化幅度均會較小；反之，如果層合管的系統剛度隨其壁厚比n的變化幅值較大，則其頻率影響系數λi的變化幅度也會增大，尤其是高階頻率影響系數會隨壁厚比n增大而明顯變化。

(a) 兩端固支

(b) 兩端自由

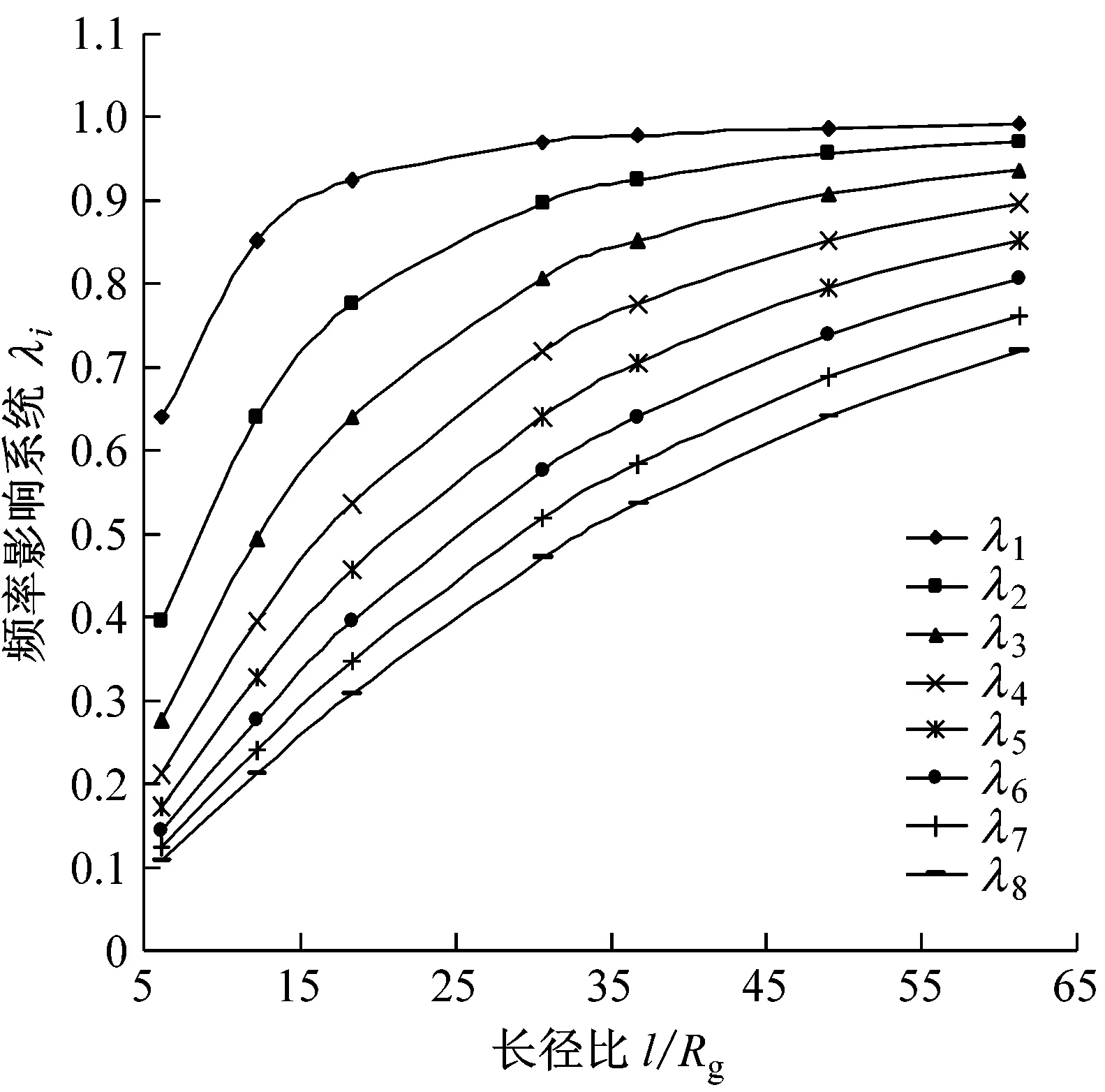
(c) 兩端簡支

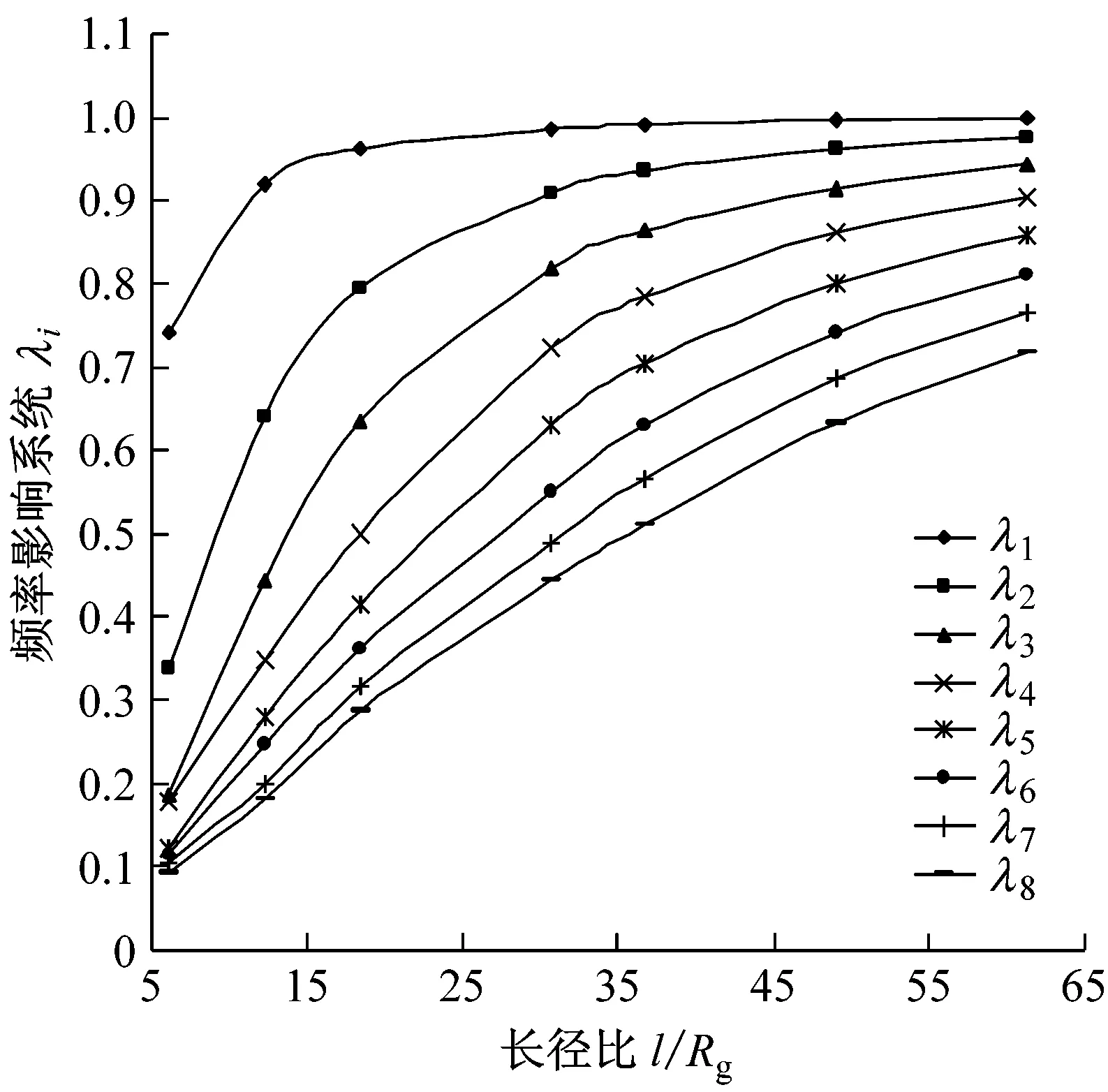
(d) 一端固支一端簡支

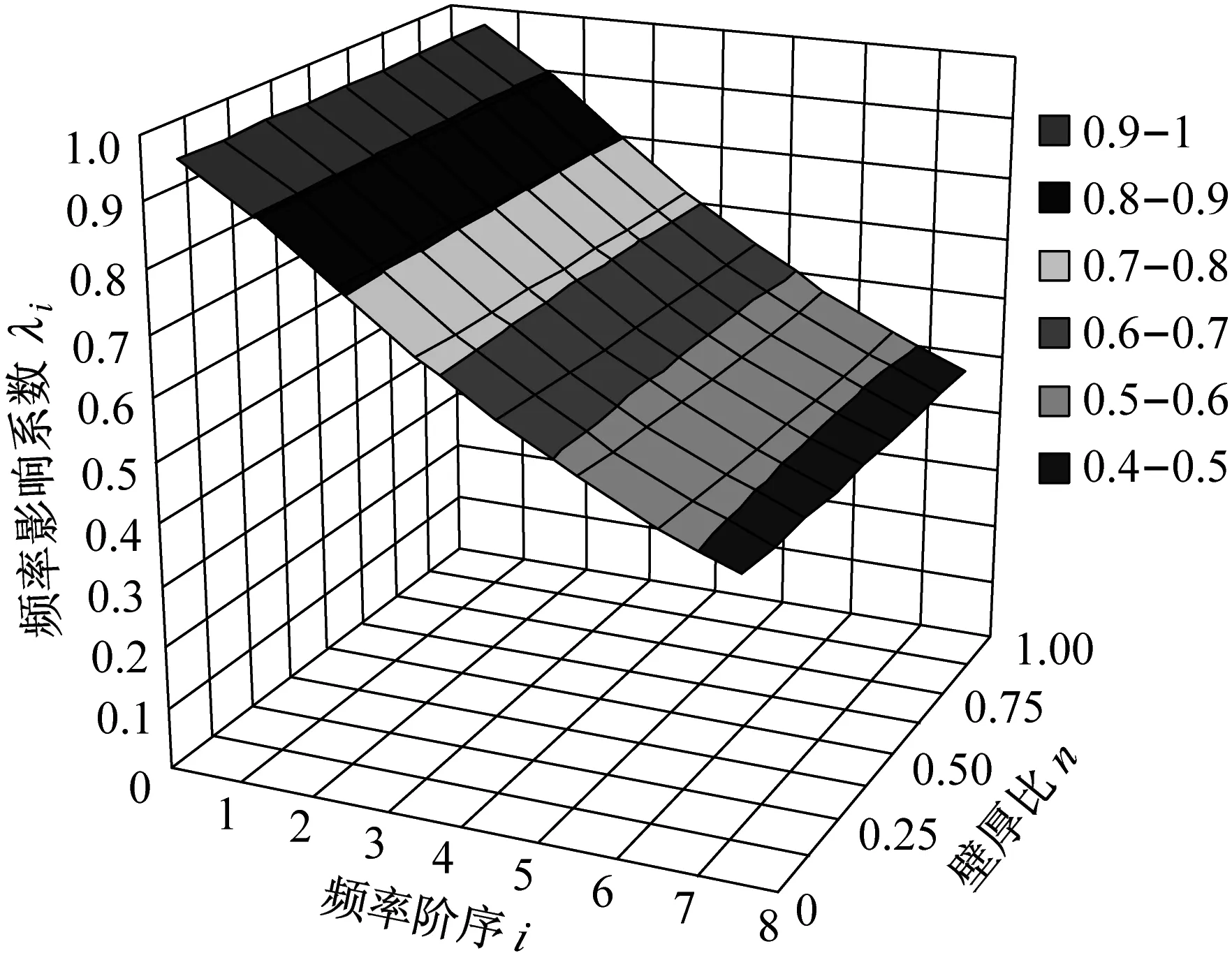
(a) 銅鋼層合管

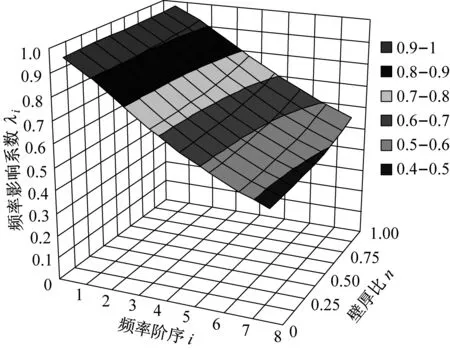
(b) 鋁鋼層合管

上述結論可以由圖7得到進一步驗證。圖7顯示了銅鋼層合管與鋁鋼層合管的參數E/kG隨其壁厚比

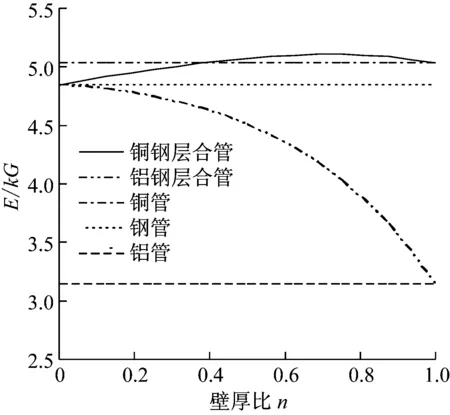
圖7 E/kG～n

4.3振型曲線的變化特性

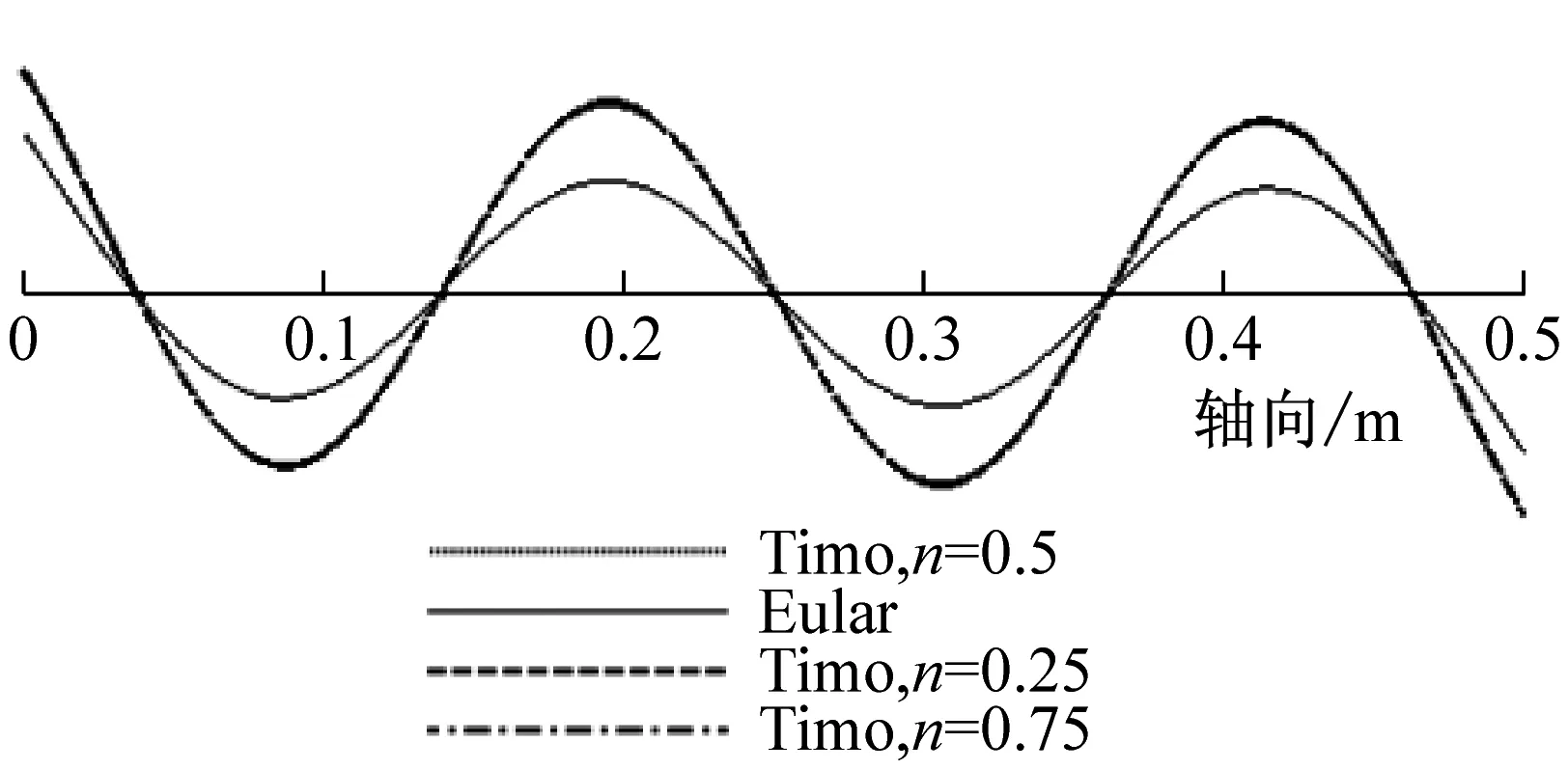
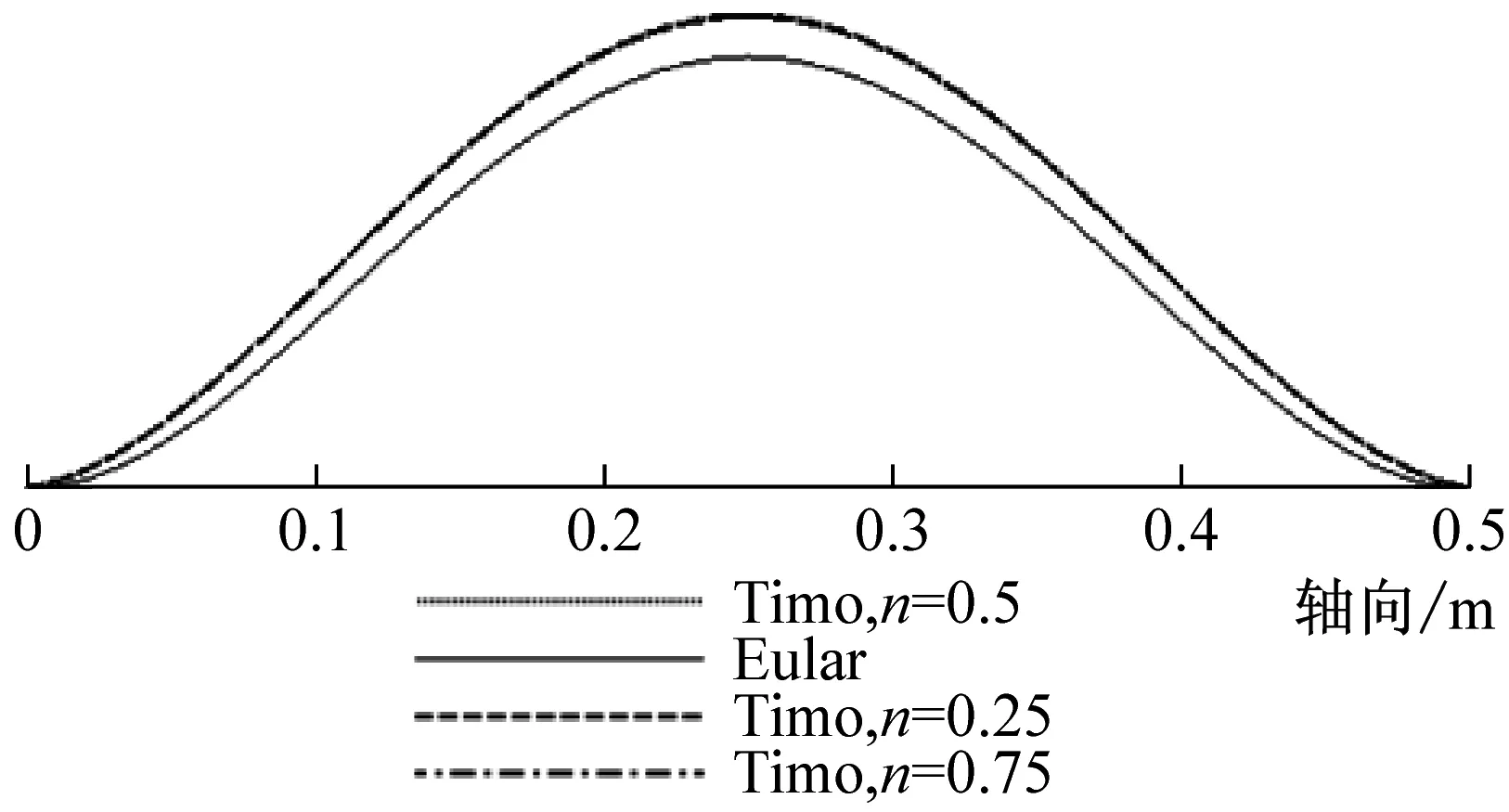
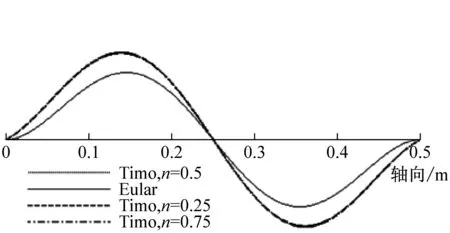
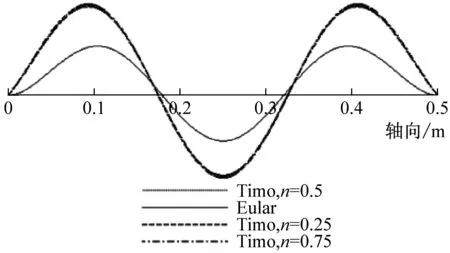
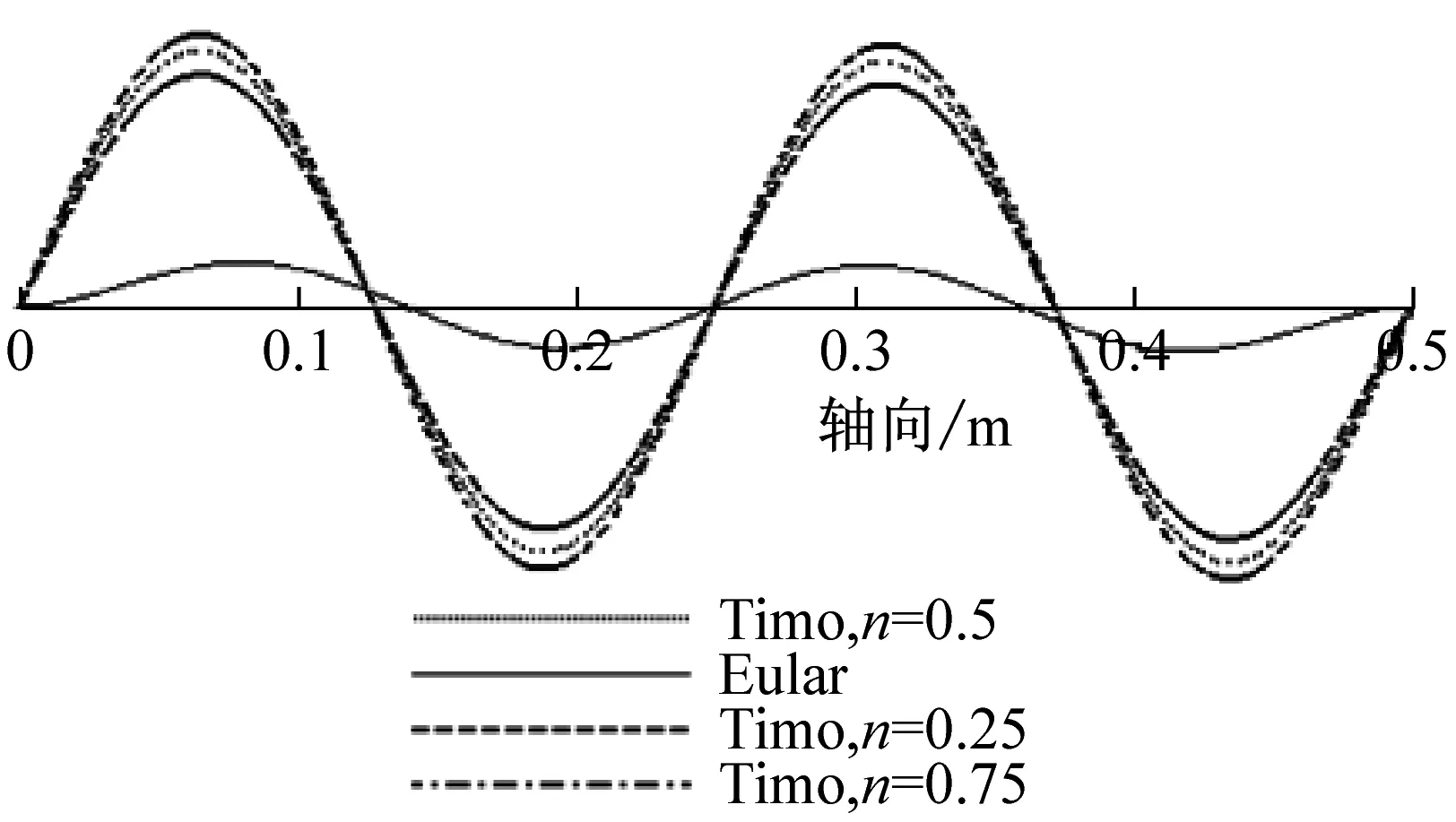
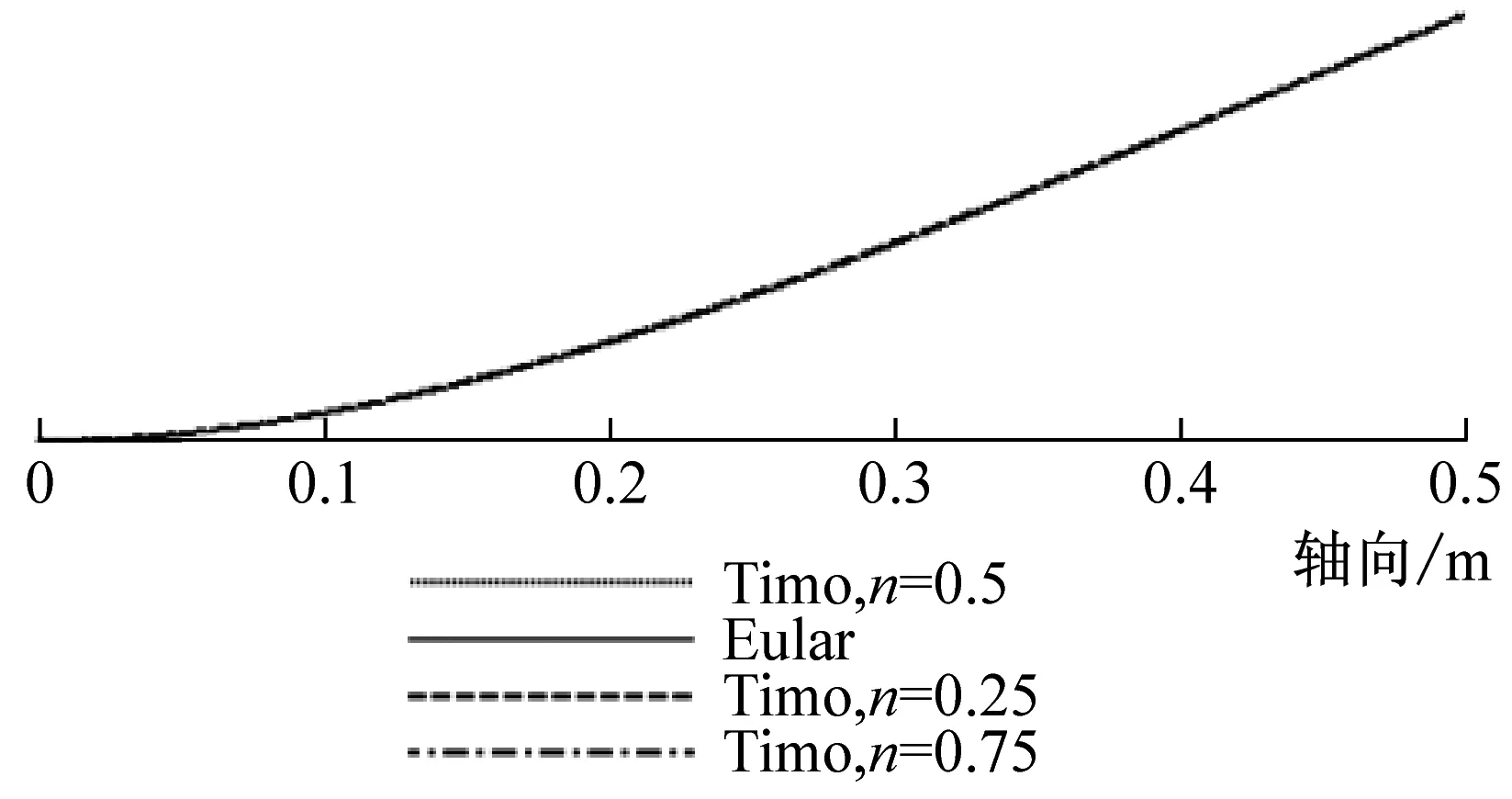
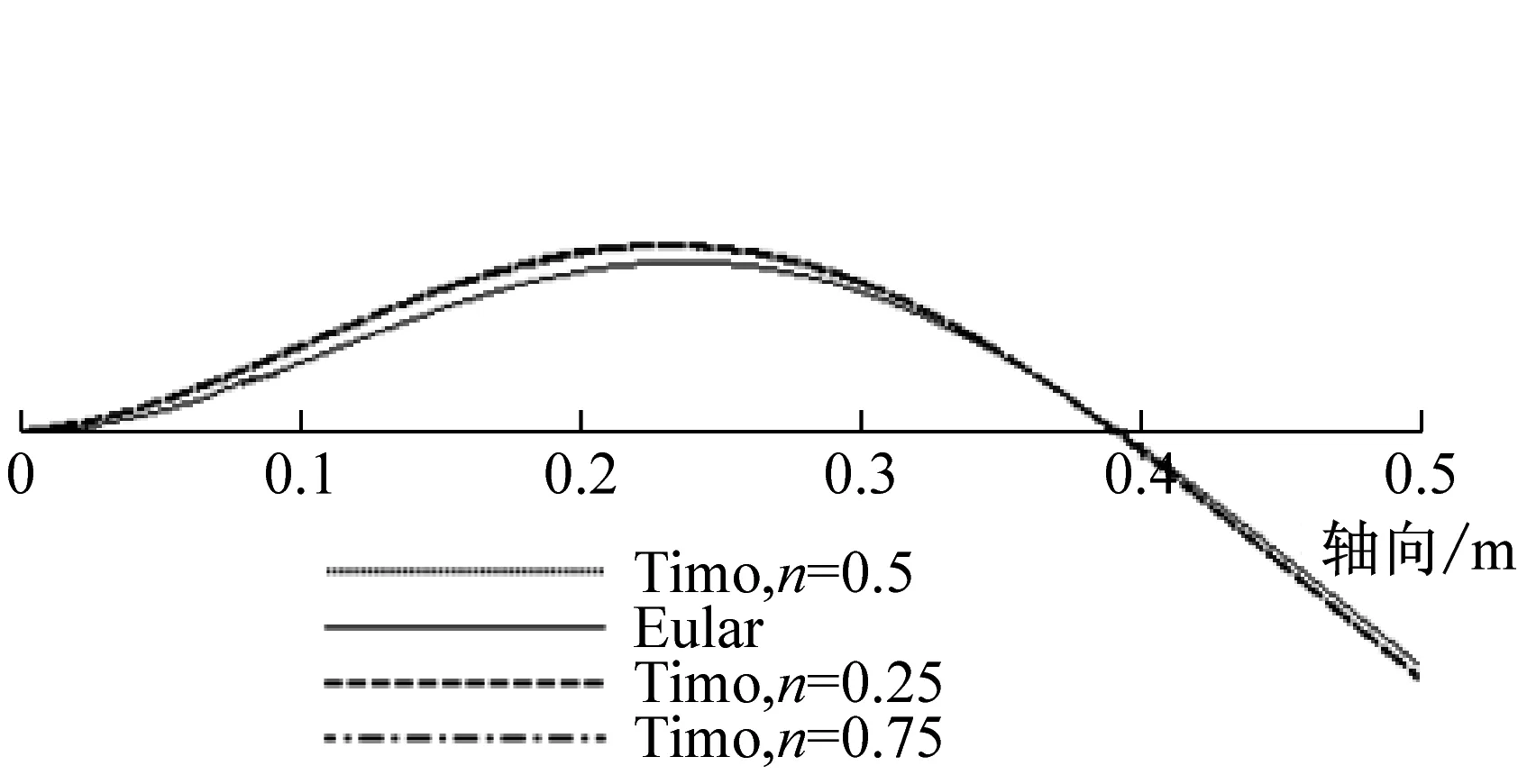
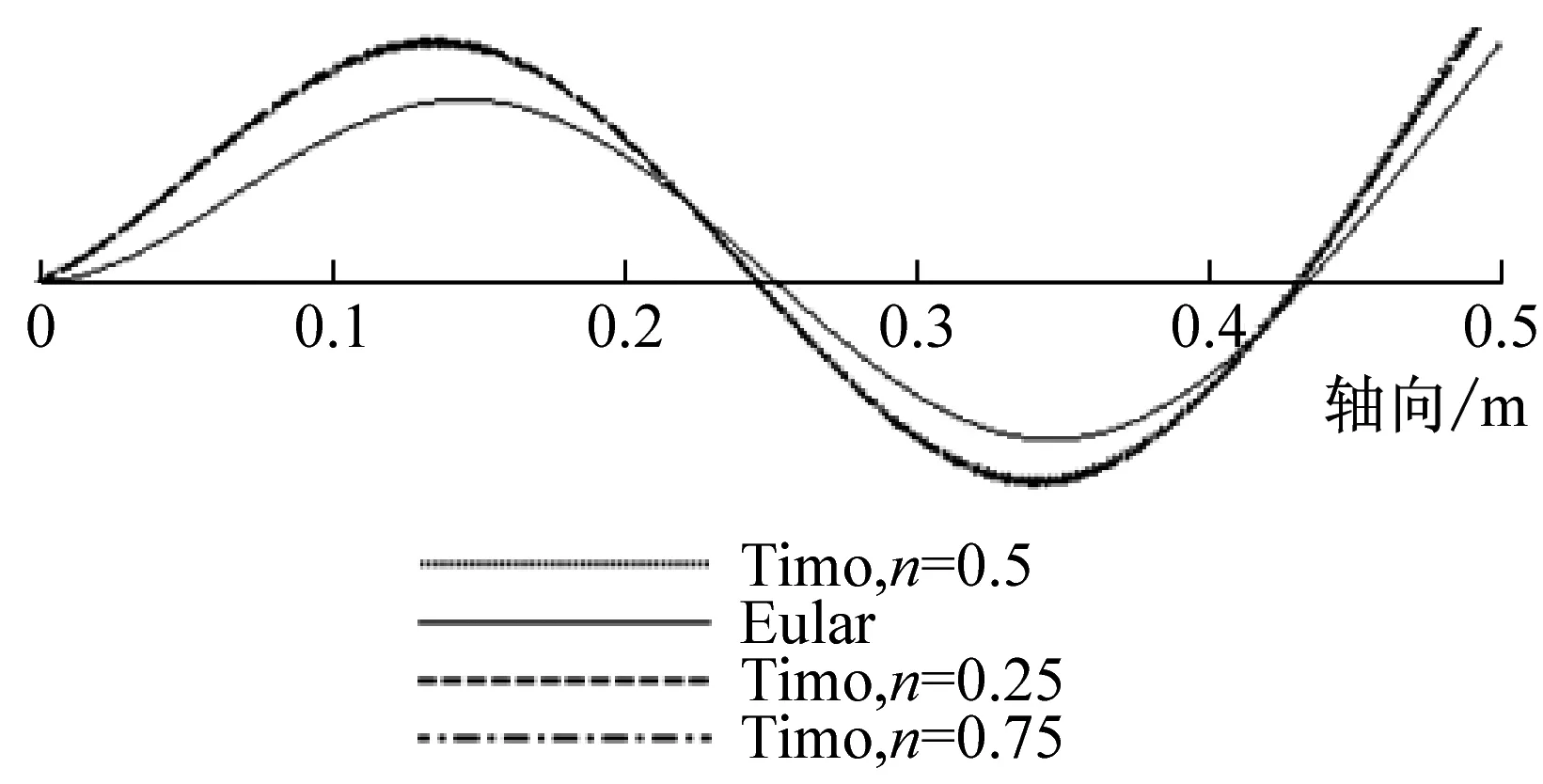
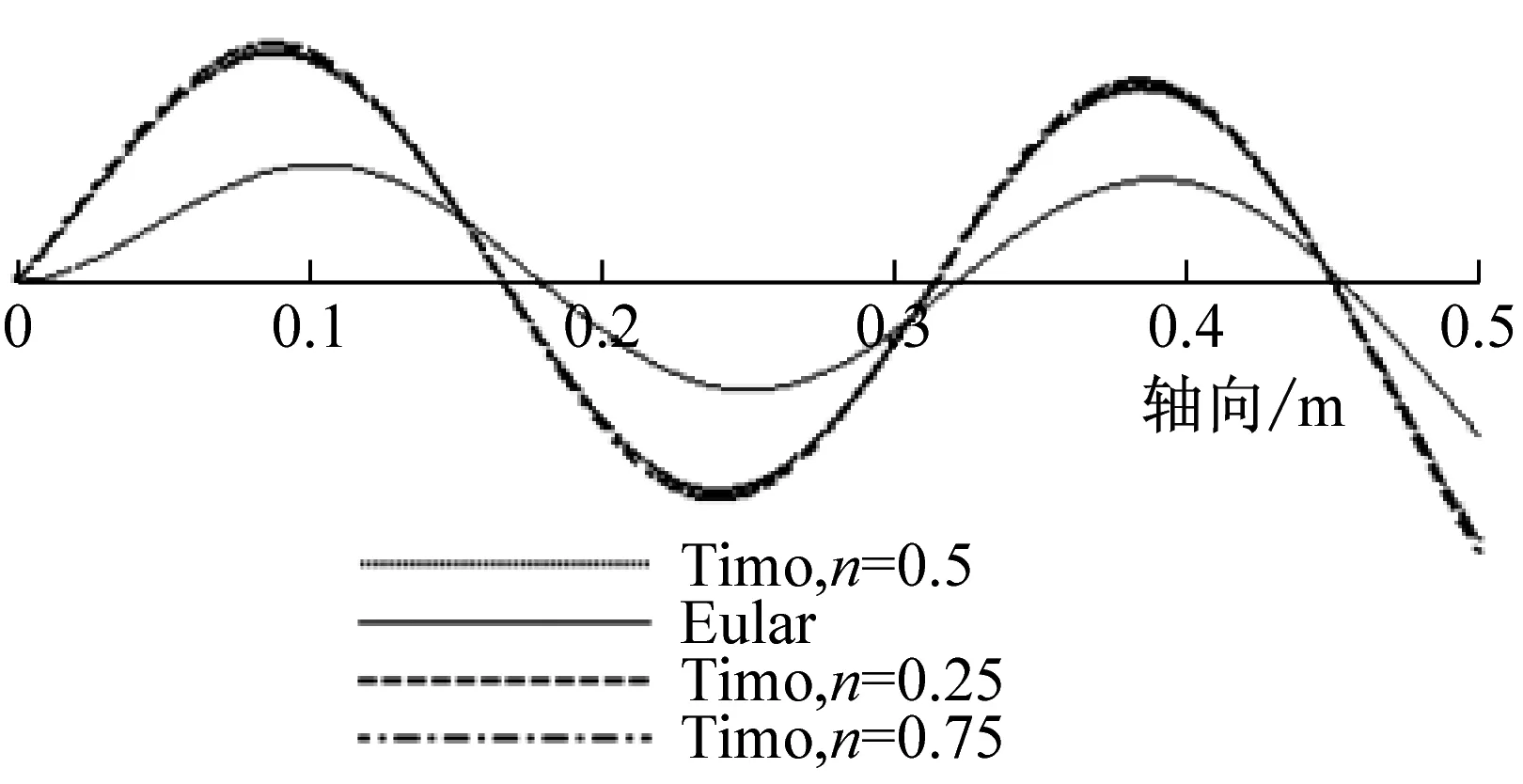
由前面理論推導可知，兩端簡支時，Euler-Bernoulli與Timoshenko梁理論的振型函數相同，且不受層合管的非勻質無量綱參數E/kG的影響。而其他三種邊界條件時，二者的振型函數不相同，且可能會受參數E/kG的影響，即振型曲線可能會隨層合管壁厚比n的變化而變化。為此，本文用MAPLE編程繪制了不同壁厚比(n=0.25，n=0.5，n=0.75)時，分別基于Euler-Bernoulli與Timoshenko理論的銅鋼層合管(長度為500 mm，總壁厚為4 mm)的前4階振型曲線，見圖8～圖10。

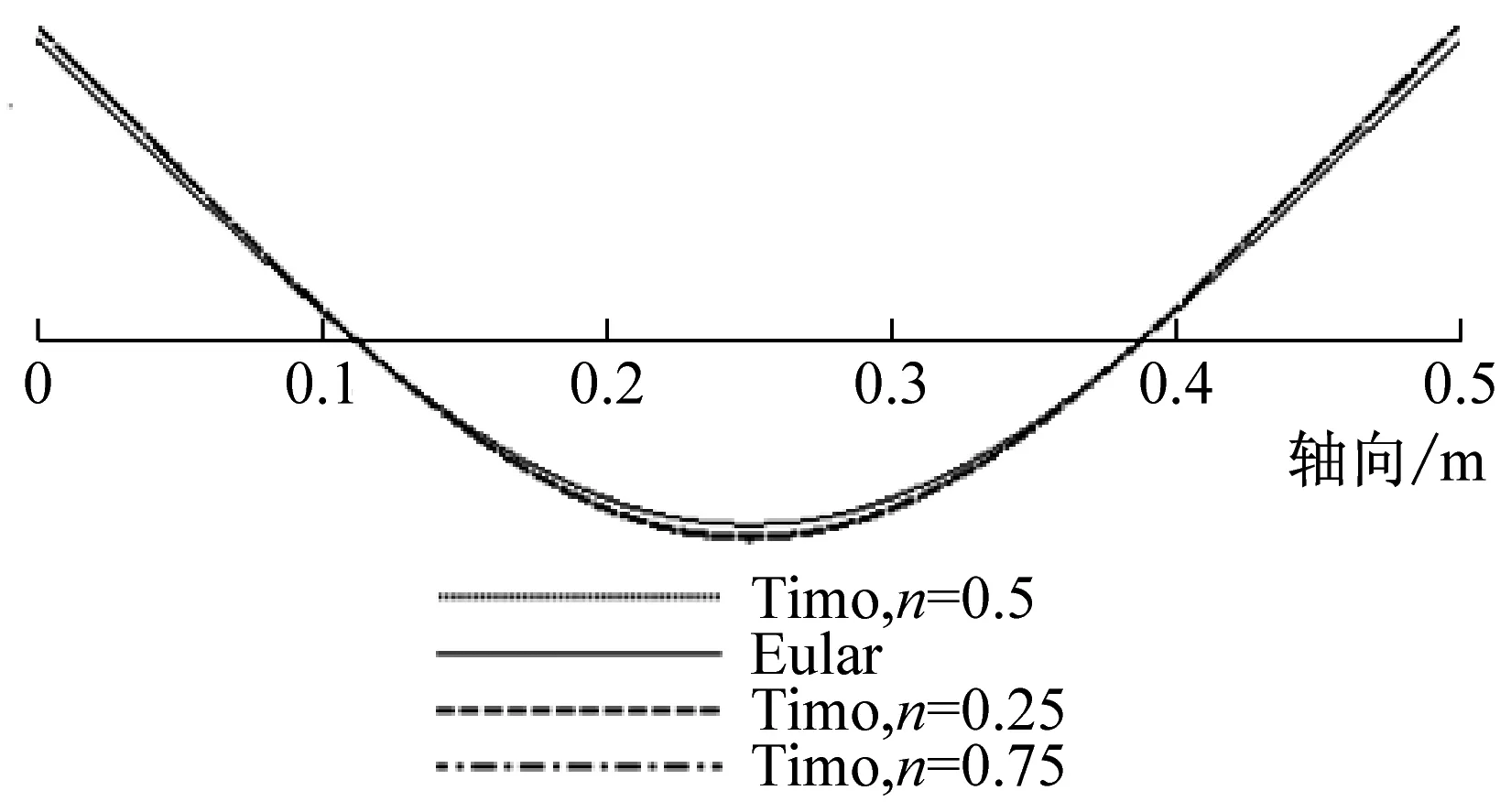
(a) 1階

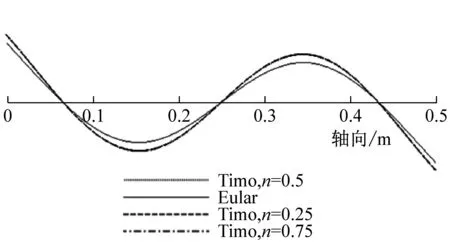
(b) 2階

(c) 3階

(d) 4階

由圖8可知，兩端自由時，基于Euler-Bernoulli理論與Timoshenko理論所解得的振型曲線波形相同，節點位置也相同；而且對層合金屬管而言，其前4階振型曲線不隨壁厚比n的變化而變化。由圖9可知，兩端固支時，上述兩種理論所解得的振型曲線波形也相同，但隨階數的增加其節點位置不再相同；對銅鋼層合管而言，其三階之后的振型曲線幅值隨壁厚比n的增大而增大，這是由于管子的剛度變大隨n的增大而變大。由圖10可知，一端固支一端自由時，由這兩種理論所解得的振型曲線的節點位置也不同，而且振動幅值也會隨層合金屬管壁厚比n的不同而變化。

總之，在兩端自由和兩端簡支邊界條件下，截面剪切變形和轉動慣量對層合管的振型曲線沒有影響，但在兩端固支和一端固支一端自由邊界條件下，其對層合管振型曲線的影響則比較顯著。

5 結 論

(1) 剪切變形和轉動慣量會降低層合金屬管的固有頻率，因此其對管子的各階頻率影響系數0.0≤λi≤1.0。而且，階序越高，層合管長徑比l/Rg越小，λi值越小。另外，當層合管長徑比l/Rg減小時，一端固支一端自由時的1階頻率影響系數λ1的減小幅度最小，兩端簡支和兩端自由時次之，而兩端固支時的減小幅度最大。

(a) 1階

(b) 2階

(c) 3階

(d) 4階

(a) 1階

(b) 2階

(c) 3階

(d) 4階

(2) 層合金屬管的剛度參數E/kG會對其頻率影響系數λi產生影響，但影響程度不同。例如，隨著壁厚比n增大，銅鋼層合管的頻率影響系數λi變化幅度非常小，而鋁鋼層合管的頻率影響系數λi變化幅度卻較大。

(3) 在兩端自由和兩端簡支邊界條件下，剪切變形和轉動慣量對層合金屬管的振型曲線沒有影響；但在兩端固支和一端固支一端自由邊界條件下，其影響則比較顯著，使管子振型曲線的節點位置發生變化。

[1] KNEZEVIC M, JAHEDI M, KORKOLIS Y P, et al. Material-based design of the extrusion of bimetallic tubes[J]. Computational Materials Science, 2014, 95: 63-73.

[2] MROZ S, STRADOMSKI G, DYJA H, et al. Using the explosive cladding method for production of Mg-Al bimetallic bars[J]. Archives of Civil and Mechanical Engineering, 2015, 15(2): 317-323.

[3] LAPOVOK R, NG H P, TOMUS D, et al. Bimetallic copper-aluminium tube by severe plastic deformation[J]. Scripta Materialia, 2012, 66(12): 1081-1084.

[4] CHITKARA N R, ALEEM A. Extrusion of axi-symmetric bi-metallic tubes: some experiments using hollow billets and the application of a generalised slab method of analysis[J]. International Journal of Mechanical Sciences, 2001, 43(12): 2857-2882.

[5] 程可,徐文斌,陸曉峰. 20/316L雙金屬復合管旋壓成形數值模擬與分析[J]. 塑性工程學報, 2015, 22(1): 119-125.

CHENG Ke, XU Wenbin, LU Xiaofeng. Numerical simulation and analysis on spinning of 20/316L bimetallic clad pipe[J]. Journal of Plasticity Engineering, 2015, 22(1): 119-125.

[6] KHANNA S, SHARMA V, SINGH S, et al. Explicit expression for temperature distribution of receiver of parabolic trough concentrator considering bimetallic absorber tube[J]. Applied Thermal Engineering, 2016, 103: 323-332.

[7] BOUZIDI S E, HASSAN M, RIZNIC J. A comprehensive flow-induced vibration model to predict crack growth and leakage potential in steam generator tubes[J]. Nuclear Engineering and Design, 2015, 292: 17-31.

[8] 楊超,范士娟. 管材參數對輸液管流固耦合振動的影響[J]. 振動與沖擊, 2011, 30(7): 210-213.

YANG Chao, FAN Shijuan. Influence of pipe parameters on fluid-structure coupled vibration of a fluid-conveying pipe[J]. Journal of Vibration and Shock, 2011, 30(7): 210-213.

[9] 羅忠,朱云鵬,韓清凱,等. 復合材料層合薄壁短圓柱殼動力學相似模型幾何適用區間確定方法[J]. 機械工程學報, 2015, 51(17): 43-51.

LUO Zhong, ZHU Yunpeng, HAN Qingkai, et al. Structure size interval of similar test model of the laminated composite thin-wall short cylinder shell[J]. Journal of Mechanical Engineering, 2015, 51(17): 43-51.

[10] 李驍,李映輝,趙華. 軸向運動層合圓柱殼體的振動特性[J]. 力學季刊, 2016, 37(2): 266-273.

LI Xiao, LI Yinghui, ZHAO Hua. Vibration characteristics of axially moving laminated cylindrical shells[J]. Chinese Quarterly of Mechanics, 2016, 37(2): 266-273.

[11] 張宇飛,王延慶,聞邦椿. 軸向運動層合薄壁圓柱殼內共振的數值分析[J]. 振動與沖擊, 2015, 34(22): 82-86.

ZHANG Yufei，WANG Yanqing，WEN Bangchun. Internal resonance of axially moving laminated thin cylindrical shells[J]. Journal of Vibration and Shock, 2015, 34(22): 82-86.

[12] WINFIELD D C, LU C H, MAO R. Beam-type modeling for the free vibration of a long thick laminated conical tube[J]. Composites Part B: Engineering, 1997, 28(5/6): 555-563.

[13] 曹志遠. 板殼振動理論[M]. 北京: 中國鐵道出版社, 1989.

[14] 郭建英,馬騰飛,劉生寶,等. 雙金屬復合管的靜動態力學特性[J]. 應用力學學報, 2016, 33(1): 168-174.

GUO Jianying, MA Tengfei, LIU Shengbao, et al. Static and dynamic mechanical characteristics of bimetallic tubes[J]. Chinese Journal of Applied Mechanics, 2016, 33(1): 168-174.

[15] EFTEKHARI M, MAHZOON M, ZIAIE RAD S. An evolutionary search technique to determine natural frequencies and mode shapes of composite Timoshenko beams[J]. Mechanics Research Communications, 2011, 38(3): 220-225.

[16] 樓夢麟,石樹中. Timoshenko固端梁特征值問題近似計算方法[J]. 應用力學學報, 2003, 20(1): 140-143.

LOU Menglin, SHI Shuzhong. An approach for solving the eigenvalue problem of Timoshenko clamped beam[J]. Chinese Journal of Applied Mechanics, 2003, 20(1): 140-143.

[17] HAN S M, BENAROYA H, WEI T. Dynamics of transversely vibrating beams using four engineering theories[J]. Journal of Sound and Vibration, 1999, 225(5): 935-988.

[18] XU Suming, WANG Xinwei. Free vibration analyses of Timoshenko beams with free edges by using the discrete singular convolution[J]. Advances in Engineering Software, 2011, 42(10): 797-806.

[19] 金晶,邢譽峰. 鐵木辛柯梁振動固有頻率的邊界元解法[J]. 北京航空航天大學學報, 2012, 38(7): 976-980.

JIN Jing, XING Yufeng. Boundary element solution method of free vibration of Timoshenko beam[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(7): 976-980.

[20] 倪振華. 振動力學[M]. 西安: 西安交通大學出版社, 1989.

[21] 郭建英,馬騰飛,劉生寶,等. 雙金屬復合翅片管振動特性的研究[J]. 振動與沖擊, 2016, 35(5): 201-206.

GUO Jianying, MA Tengfei, LIU Shengbao, et al. Vibration characteristics of bimetallic finned tube[J]. Journal of Vibration and Shock, 2016, 35(5): 201-206.

[22] COWPER G R. The shear coefficient in Timoshenko’s beam theory[J]. Journal of Applied Mechanics,1966, 33(3): 393-398．

Effectsofsheardeformationandrotaryinertiaonthevibrationoflaminatedthick-walledshorttubes

GUOJianying1,BAIYanyan2

(1. College of Mining Engineering, Taiyuan University of Technology, Taiyuan 030024, China; 2. College of Mechanical Engineering, Taiyuan University of Technology, Taiyuan 030024, China)

The effects of non-homogeneit, shear deformation and rotary inertia are necessary to be taken into account in the vibration analysis of laminated metal thick-walled short tubes. Based on the Timoshenko’s beam theory, the analytical expressions of the frequencies and modal functions of laminated metal tubes were deduced under four kinds of boundary conditions: hinged-hinged, clamped-clamped, free-free and clamped-free. The natural frequencies of copper-steel laminated tubes were solved and the mode shapes were mapped by use of the computer algebra system MAPLE for these four cases. The natural frequencies of three copper-steel laminated tubes with different lengths were also measured by using both the method of hammer tests and the finite element modal analysis. The theoretical solutions of the first three natural frequencies of the copper-steel tubes were compared with the measured values, the maximum error being -4.56%, and also compared with the finite element results, the maximum error being -0.76%. The influential coefficients of shear deformation and rotary inertia on the frequencies of laminated metal thick-walled short tubes were solved. The variations of the frequency influential coefficients and modal shapes along with the boundary condition, frequency order, aspect ratio, non-homogeneous material parameter of laminated metal tubes were also investigated.

laminated metal thick-walled short tubes; shear deformation; rotary inertia; frequency influential coefficient; mode shape

TB123

A

10.13465/j.cnki.jvs.2017.21.017

山西省自然科學基金(2013011025-2)；山西省研究生教育改革研究課題(2016JG40)

2016-05-23 修改稿收到日期：2016-09-06

郭建英 女，博士，副教授，1972年11月生