具有非線性發(fā)生率的多易感群體的傳染病模型研究

商佩佩+袁朝暉

摘 要 本文主要研究一類具有Beddington-DeAngelis發(fā)生率的多易感群體的傳染病模型.首先得到基本再生數(shù)R0，然后通過構(gòu)造Lyapunov泛函和LaSalle不變原理得到了平衡點(diǎn)的全局漸近穩(wěn)定條件.

關(guān)鍵詞 非線性發(fā)生率；多易感種群；Lyapunov泛函；LaSalle不變原理；全局漸近穩(wěn)定性

中圖分類號 O175.14 文獻(xiàn)標(biāo)識碼 A 文章編號 1000-2537（2017）05-0071-06

Study on Epidemic Models with Nonlinear Incidence Rate and Differential Susceptibility

SHANG Pei-pei*， YUAN Zhao-hui

（College of Mathematics and Econometrics， Hunan University， Changsha 410082， China）

Abstract This paper investigates a class of epidemic model with Beddington-DeAngelis incidence rate and differential susceptibility. The basic reproduction number R0 is first given， after which some sufficient conditions ensuring the stability of the system are obtained by constructing Lyapunov functional and using the LaSalle invariable principle.

Key words nonlinear incident rate； differential susceptibility； Lyapunov functional； LaSalle invariable principle； globally asymptotical stability

傳染病歷來就是危及人類健康的大敵，由于其傳染性和流行性特征，一旦爆發(fā)很有可能大面積感染.在2014年西非的埃博拉疫情中，確診死亡率高達(dá)88%.長期以來，人們運(yùn)用多種方法研究傳染病的發(fā)病機(jī)理和傳播規(guī)律，以期控制和消除傳染病[1].傳染病動(dòng)力學(xué)是通過建立數(shù)學(xué)模型，對傳染病的流行規(guī)律進(jìn)行定性、定量的研究[2，3]. 在經(jīng)典的傳染病模型中，大量使用的是雙線性發(fā)生率和標(biāo)準(zhǔn)發(fā)生率[4，5].為了解釋傳染病傳播過程中出現(xiàn)的一些復(fù)雜現(xiàn)象，近年來，又有一些能更好地模擬實(shí)際情況的非線性發(fā)生率被提出，如在文獻(xiàn)[6]中，Capasso等提出了接觸率可能依賴于患病者個(gè)體的飽和發(fā)生率βSI/（1+αI）和含有βSf（I）形式的非線性發(fā)生率. 文[7-9]分別針對一些特殊的具有非線性發(fā)生率的多種群傳染病模型進(jìn)行了討論.

自然界中，受性別、年齡階段、成長環(huán)境等多種因素的影響，不同易感群體由于自身免疫力及感染機(jī)會(huì)等存在差異，對傳染病的易感程度并非完全相同，因此對多易感群體的傳染病模型進(jìn)行研究非常必要.

假設(shè)HIV易感者被HIV感染后存在一個(gè)潛伏期，處于潛伏期的感染者并不具有傳染性，只有越過潛伏期的HIV感染者才具有傳染性，并且由HIV感染者轉(zhuǎn)化為艾滋病患者后，患者的活動(dòng)能力由于受到了限制而無法傳染HIV給易感者.基于此，本文將建立一個(gè)具有非線性發(fā)生率的多易感群體的特殊艾滋病傳播模型模型，采用一種特殊的非線性發(fā)生率βkSkI1+mSk+nI（即Beddington-DeAngelis發(fā)生率[10]），并得到系統(tǒng)平衡點(diǎn)全局漸近穩(wěn)定的條件.

1 模型與理論

1.1 模型的建立

符號說明及假設(shè)：

Sk，k=1，2，…，N. 易感者按其對HIV免疫力強(qiáng)弱、感染機(jī)會(huì)大小等的不同劃分成N個(gè)不同的易感群體（注：對于處于潛伏期的患者E類和具有傳染性的患者Ⅰ類不進(jìn)行類別內(nèi)分組）；

ak≥0： 第k類易感群體的輸入率；

d≥0： 自然死亡率；

μ≥0： 從處于潛伏期的感染者變?yōu)榫哂袀魅拘缘幕疾≌叩霓D(zhuǎn)換系數(shù)；

α≥0： 處于患病早期的患者轉(zhuǎn)化為患病晚期患者的轉(zhuǎn)換系數(shù)；

γ≥0： 因病死亡系數(shù)；

βk≥0： 群體Sk中成員與早期患病者的有效接觸率和易感程度.

其中，S，E，I，A分別表示HIV易感者、潛伏期中的HIV感染者、已具傳染力的HIV感染者和艾滋病患者的數(shù)目.顯然系統(tǒng)（1）的前面N+2個(gè)方程獨(dú)立于最后的方程，因此下面僅考慮系統(tǒng)（1）的前N+2個(gè)方程構(gòu)成的系統(tǒng)：

對于方程組（2），先假設(shè)初始條件為

其中，Sk（0）>0（k=1，2，…，N），E（0）>0，I（0）>0.

易知（2）存在唯一的正解.

1.2 解的有界性

注意到由（2）的前N個(gè)方程可以得到S′k≤ak-dSk，進(jìn)而有

綜上，Γ是系統(tǒng)（2）的正不變集.

1.3 平衡點(diǎn)和基本再生數(shù)

因此，h（I）在[0，+∞）上連續(xù)單調(diào)遞增，于是得出F（I）是[0，+∞）上的連續(xù)單調(diào)減函數(shù).注意到F（0）=R0-1，F(xiàn)（+∞）=-1，所以當(dāng)R0>1時(shí)，F(xiàn)（I）必有唯一的正零點(diǎn)I*，然后將I*逐一代入方程組（5）的前N個(gè)方程和最后一個(gè)方程，可將S*k，E*分別用I*表示出來.以上部分證明出，當(dāng)R0>1時(shí)，系統(tǒng)（2）存在唯一的地方病平衡點(diǎn)E*=（S*1，S*2，…，S*N，E*，I*）∈intΓ.endprint

1.4 穩(wěn)定性

定理1 若R0≤1，則無病平衡點(diǎn)E0在Γ中是全局漸近穩(wěn)定的.

證 令

僅當(dāng)Sk=S*k，E=E*，I=I*（k=1，2，…，N）時(shí)，等號成立.

因此，對所有Sk，E，I>0（k=1，2，…，N），V′≤0成立，故地方病平衡點(diǎn)E*是穩(wěn)定的.當(dāng)且僅當(dāng)Sk=S*k，E=E*，I=I*（k=1，2，…，N）時(shí)，V′=0，即Γ={（Sk，E，I）|V′=0，k=1，2，…，N}的最大緊不變集為單點(diǎn)集{E*}，則根據(jù)LaSalle不變原理，當(dāng)R0>1時(shí)，地方病平衡點(diǎn)E*在IntΓ中是全局漸近穩(wěn)定的.

2 數(shù)值仿真

這里將對系統(tǒng)（2）進(jìn)行數(shù)值仿真，對系統(tǒng)內(nèi)參數(shù)取值情況如下：

取k=3，a1=0.5，a2=0.48，a3=0.51，β1=d=m=n=μ=0.1，α=0.2，β2=0.12，β3=0.13，此時(shí)易算得R0=1.94>1. 取初值（S1（0），S2（0），S3（0），E（0），I（0））=（24.5，24.5，24.5，0.02，5）， 仿真結(jié)果見圖1.

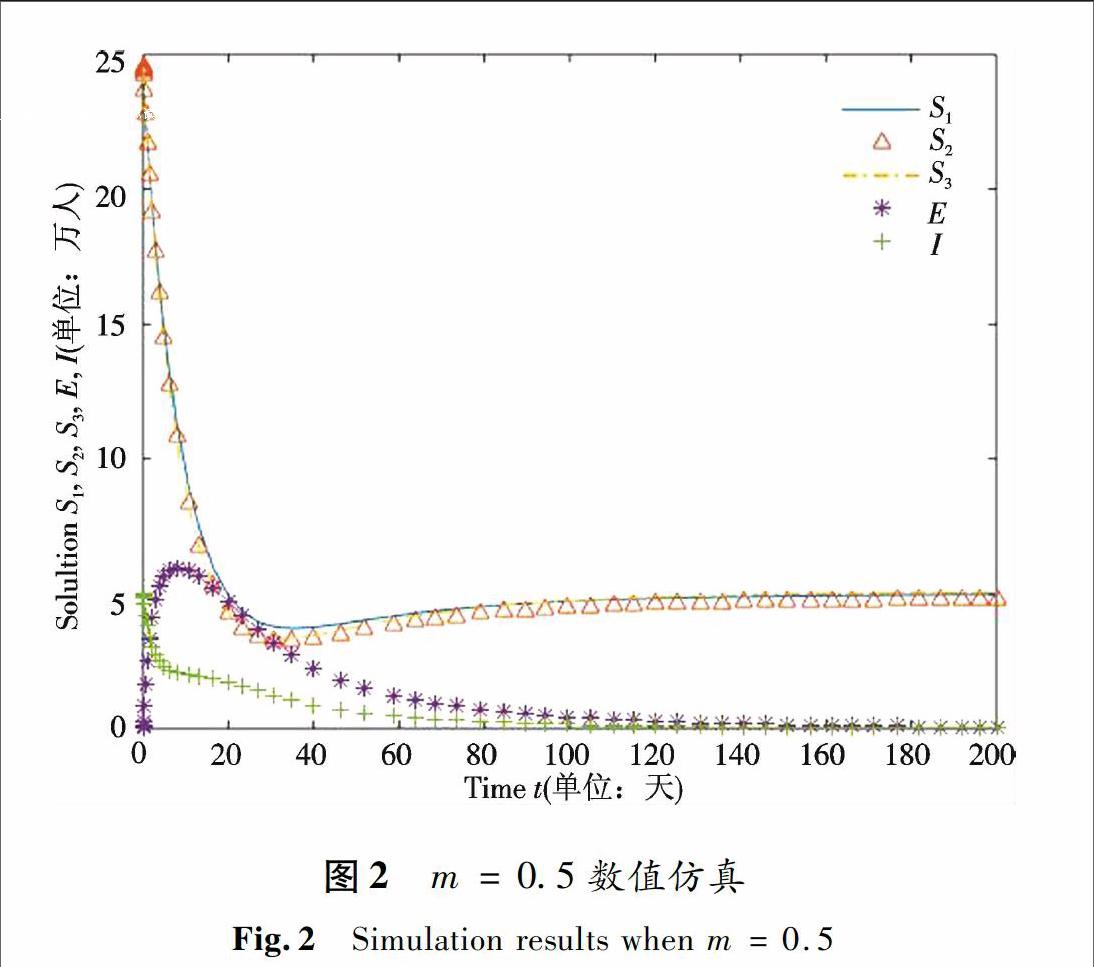
若保持其他參數(shù)和初值不變，取參數(shù)m=0.5， 此時(shí)R0=0.83<1. 仿真結(jié)果見圖2.

由仿真結(jié)果可以看出， 當(dāng)R0>1時(shí)， 系統(tǒng)是全局漸近穩(wěn)定并一致持久的，說明疾病爆發(fā)后不會(huì)持續(xù)蔓延，系統(tǒng)在一定時(shí)間后會(huì)保持穩(wěn)定；通過控制參數(shù)m使其變大，可以得到R0<1， 系統(tǒng)的無病平衡點(diǎn)是全局漸近穩(wěn)定和一致持久的， 并且疾病在一段時(shí)間后會(huì)消亡.

參考文獻(xiàn)：

[1] 馬知恩，周義倉，王穩(wěn)地.傳染病動(dòng)力學(xué)的數(shù)學(xué)建模與研究[M].北京：科學(xué)出版社，2004.

[2] 陸征一，周義倉.數(shù)學(xué)生物學(xué)進(jìn)展[M].北京：科學(xué)出版社，2006.

[3] 張仲華.具一般非線性隔離函數(shù)和接觸率的染病年齡SIRS模型平衡點(diǎn)的存在性及穩(wěn)定[J].高校應(yīng)用數(shù)學(xué)學(xué)報(bào)：A輯， 2011，26（1）：46-54.

[4] DRIESSCHE P， WANG L. Impact of group mixing on disease dynamics[J]. Math Biosci， 2010（228）：71-77.

[5] HETHCOTE H. Qualitative analyses of communicable disease models[J]. Math Biosci， 1976（7）：335-356.

[6] CAPASSO V，SERIO G.A Generalization of the kernmck-mckendrick deterministic epidemic model[J].Math Biosci， 1978（42）：41-61.

[7] YUAN Z H， WANG L. Global stability of epidemiological models with group mixing and nonlinear incidence rates [J]. Nonlinear Anal Real World Appl， 2010（11）：995-1004.

[8] YUAN Z H， ZOU X F. Global threshold property in an epidemic model for disease with latency spreading in a heterogeneous host population [J]. Nonlinear Anal Real World Appl， 2010（11）：3479-3490.

[9] KUNIYA T. Global stability analysis with a discretization approach for an age-structured multigroup SIR epidemic model [J]. Nonlinear Anal Real World Appl， 2011（12）： 2640-2655.

[10] HUANG G， MA W， TAKEUCHI Y. Global properties for virus dynamics model with Bedding-DeAngelis functional response[J]. Appl Math Lett， 2009（22）：1690-1693.

[11] LASALLE J. The Stability of Dynamics Systems[M]. Philadelphia： SIAM， 1976.endprint