基于模型預測控制的智能車輛路徑跟蹤控制器設計＊

王藝 蔡英鳳 陳龍 王海 李健 儲小軍

（江蘇大學，鎮江 212013）

基于模型預測控制的智能車輛路徑跟蹤控制器設計＊

王藝 蔡英鳳 陳龍 王海 李健 儲小軍

（江蘇大學，鎮江 212013）

為提高智能車輛路徑跟蹤的魯棒性，基于模型預測控制原理提出了一種路徑跟蹤控制方法。該方法對車輛的3自由度非線性動力學模型進行線性化，得到線性時變模型和預測方程，并將包括控制量、控制增量等約束納入二次規劃的求解過程，同時考慮質心側偏角、路面附著系數等影響操穩特性的約束條件。在CarSim和MATLAB/Simulink平臺上以不同車速進行了雙移線工況下的聯合仿真，結果顯示，該控制器可較好地實現路徑跟蹤，并保持較好的穩定性。

1 前言

自動轉向控制作為智能車輛自動化駕駛控制的關鍵技術[1]，通過控制轉向角操控車輛側向運動以實現路徑跟蹤。很多模型算法可以實現較高精度的路徑跟蹤，應用較多的有PID算法[2]、純點追蹤控制[1]、前饋-反饋控制[3]、預瞄跟蹤最優控制[4～5]、線性二次型調節器（Linear Quadratic Regulator，LQR）跟蹤控制器[6]和模型預測控制等方法[4]。

模型預測控制（Model Predictive Control，MPC）于20世紀70年代被提出，目前已廣泛應用于各個領域[7]。模型預測控制具有預測模型、滾動優化和反饋校正等基本特征[8]，尤其適用于不易建立精確數學模型且存在約束條件的控制系統，在解決智能車輛在高速和冰雪等復雜路面條件下的路徑跟蹤控制問題上具有獨特的優勢[9]。車輛的行駛環境復雜多變，充滿各種不確定因素，所以不論是車輛自主駕駛還是由駕駛員控制車輛，都需要根據周圍的環境信息實時決定下一步的行駛計劃，這一點同模型預測控制的思想一致[10]。近年來，MPC已廣泛應用于智能車輛路徑跟蹤控制[11]。

為了提高智能車輛在中低速工況下跟蹤目標路徑的準確性，本文從智能車輛對路徑跟蹤控制的實時性和魯棒性出發，同時強調車輛行駛穩定性，對智能車輛的自主轉向進行研究。首先建立車輛3自由度動力學模型，并構建預測方程，將問題轉化為二次規劃問題，然后確定各約束條件，最后利用CarSim與MATLAB/Simulink平臺進行聯合仿真，驗證控制效果。

2 車輛動力學建模

整車屬于復雜的系統，因此在進行車輛動力學建模時，需要對模型進行一定程度的簡化。本文主要的研究目標是實現車輛較好、較快地跟蹤期望路徑，不需要研究車輛的懸架特性；同時，考慮到本文基于模型預測原理進行路徑跟蹤控制，需要盡可能簡化約束以減小計算量。基于此，本文作如下簡化：

a.忽略路面的凹凸不平，假設車輛始終行駛在平坦路面上；

b.忽略懸架作用和車輛的垂向運動；

c.忽略車輛本身轉向系統的影響，以前輪轉角作為系統輸入；

d. 假設左、右輪胎完全一致，只考慮輪胎的側偏特性且工作于線性區；

e.忽略空氣阻力和滾動阻力。

用單軌模型描述車輛運動，構建只有縱向、橫向、橫擺3個自由度的車輛模型，如圖1所示。

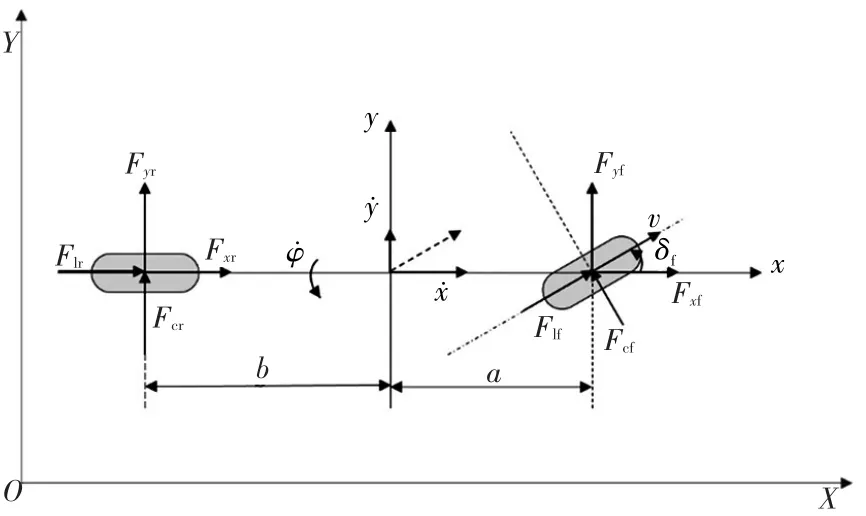
圖1 3自由度車輛模型

據此建立的車輛動力學模型為：

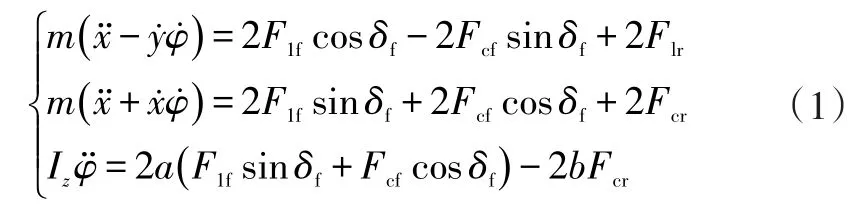
其中，Fcf、Fcr分別為車輛前、后輪胎所受的側向力，與輪胎的側偏剛度、側偏角有關；Flf、Flr分別為車輛前、后輪胎所受縱向力，與輪胎的縱向剛度、滑移率有關；Fxf、Fxr分別為車輛前、后輪胎在x方向所受的力；Fyf、Fyr分別為車輛前、后輪胎在y方向所受的力；δf為車輛前輪轉角；φ為車輛橫擺角；a為前軸到質心的距離；b為后軸到質心的距離；Iz為車輛繞乙軸的轉動慣量。

根據前文假設，本文涉及的輪胎力用線性函數近似表示。引入側偏剛度、側偏角、縱向剛度、滑移率后，輪胎力可以表示為：

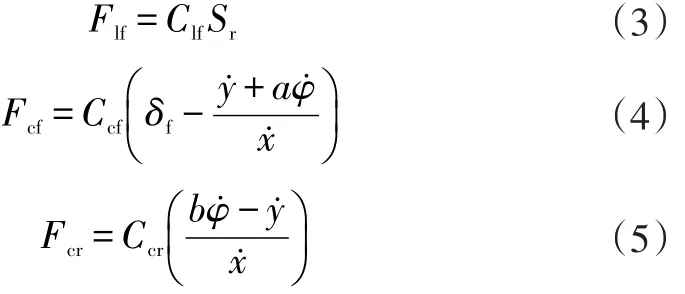
式中，Ccf、Ccr分別為車輛前、后輪胎的側偏剛度；Clf、Clr分別為車輛前、后輪胎的縱向剛度；Sf、Sr分別為車輛前、后輪胎的滑移率。

式（1）所描述的車輛動力學模型中存在一些三角函數，影響計算的復雜程度，為了減小計算量，此處假設車輛前輪轉角以及輪胎側偏角均處于較小的角度區間，所以三角函數可轉換成：

至此，車輛的動力學方程轉變為：

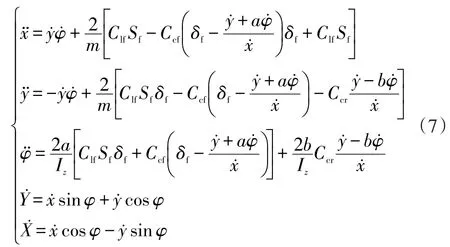
3 控制器設計

3.1 線性時變模型

以線性時變模型作為預測模型的控制算法叫做線性時變模型預測控制算法。相較于非線性模型預測控制，線性時變模型計算更加簡單，實時性好，因此應用相當廣泛[8]。

前文所得車輛模型為非線性模型，經過線性化得到線性時變方程：

式中，A(t)=?f/?ξ；B(t)=?f/?u；C=(0,0,0,0,1,0)T。

對線性時變方程采用一階差商的方法進行離散化后得到離散的狀態空間方程：

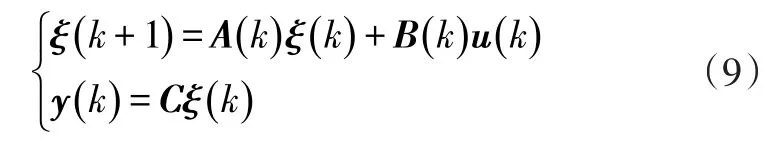
式中，A(k)=I+TA(t)；B(k)=TB(t)；T為采樣周期；I為單位矩陣。

引入增量模型后，狀態空間方程為：

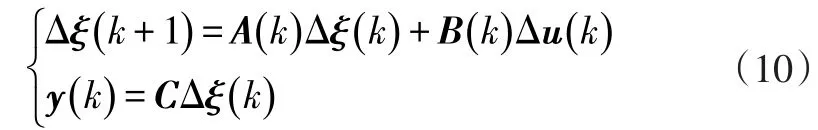
3.2 預測方程

預測方程是模型預測控制中的重要部分，需計算出未來一段時間系統的輸出。先將式（9）轉換成：

至此可以得到新的狀態空間表達式：

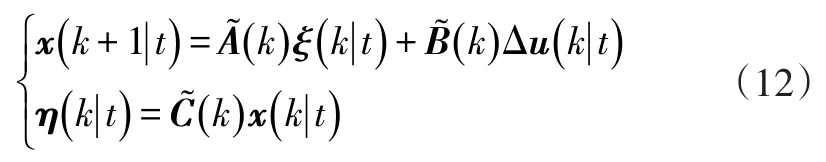
根據模型預測控制的基本理念，設Np為預測時域，Nc為控制時域，Nc≤Np。定義k時刻時系統輸出為：

定義k時刻系統輸入為：

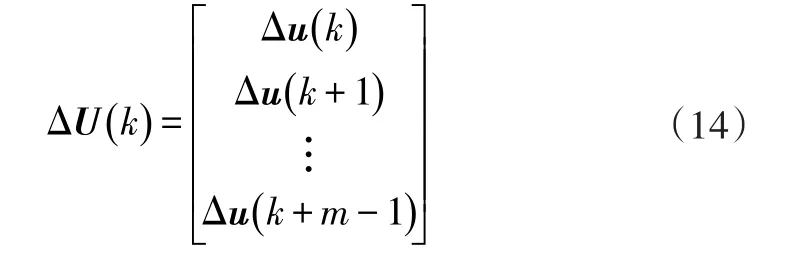
依據模型預測控制原理的基本相關理論可以得到系統未來k時刻的輸出方程為：

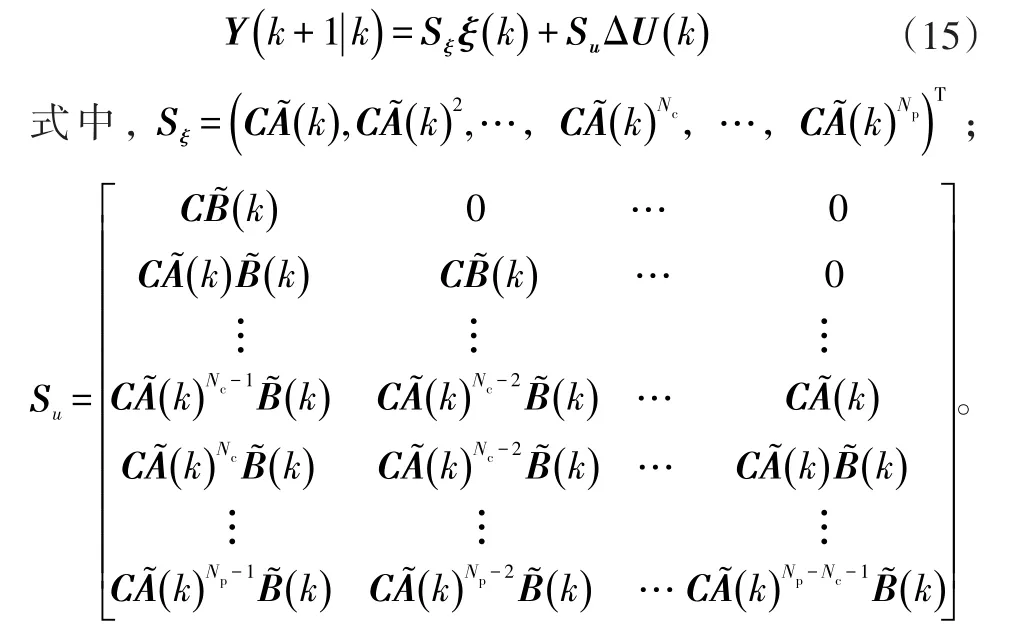
3.3 構建約束條件

在設計模型預測控制器時，除了考慮控制量及其增量的約束，還需考慮車輛的動力學約束。由于前文進行動力學建模時，輪胎部分的動力學特性采用了近似直線的表達式，所以首先引入輪胎側偏角約束。

此外，汽車的操縱穩定性不僅關系到行駛時的操縱方便，也決定著車輛高速行駛下的安全性能，同時，決定了車內乘員的乘坐舒適性。因此，本文除了正常的動力學約束外，同時引入質心側偏角約束和路面附著條件約束，以保證車輛的操穩特性和乘坐舒適性。

各約束條件如下：

a.輪胎側偏角約束

根據輪胎的側偏特性，在輪胎側偏角不超過5°時，側偏角與側偏力成線性關系。根據前文構建動力學模型時提出的小角度約束，設定前輪側偏角約束條件為：-2°≤β≤2°。

b.質心側偏角約束

質心側偏角影響著車輛的穩定性，某公司關于車輛穩定性研究得出的結果顯示：在附著條件良好的干燥瀝青路面上，車輛穩定行駛的質心側偏角極限可以達到±12°；而在附著系數較低的冰雪路面上，極限值近似為±2°[9]。考慮到實際正常行駛時，達不到極限區間，故本文將質心側偏角的約束條件設置為：-10°≤β≤10°（良好路面），-1°≤β≤1°（冰雪路面）。

c.附著條件約束

汽車的動力性能還受到路面附著系數的影響。路面附著條件較好時，該因素對車輛行駛影響不大，當條件較為惡劣時，則會對車輛的動力性和乘客的舒適性產生影響[9]。此外，限定過小的約束條件會造成控制器的求解失敗。因此，本文將路面附著系數的約束設置為軟約束。當車輛縱向勻速行駛時，車輛的側向加速度和路面附著系數存在以下關系：

因此，可以將路面附著條件約束寫成：

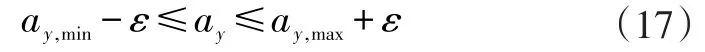
至此，將所有約束納入二次規劃的求解過程。

3.4 模型預測控制器

由于車輛動力學模型本身的復雜性，在設計目標函數時加入松弛因子，得到目標函數為：

綜合考慮目標函數和約束條件，控制器需要在每個控制周期內需解決：

在每個控制周期內，系統都需對優化問題（19）進行求解，求解結果為控制時域內的一系列包含控制增量和松弛因子的控制序列，該序列的第1個元素將作為實際的控制增量作用于系統。進入到下一個周期后，系統重復上述過程，循環實現車輛對目標路徑的跟蹤。

4 仿真結果

本文選取雙移線作為目標路徑，仿真時，路面附著系數取0.85，車輛的初始位置為坐標原點，控制器的預測時域Np=20，控制時域Nc=3，分別以18 km/h、36 km/h、54 km/h的縱向速度進行聯合仿真，控制器其他參數如表1所示。

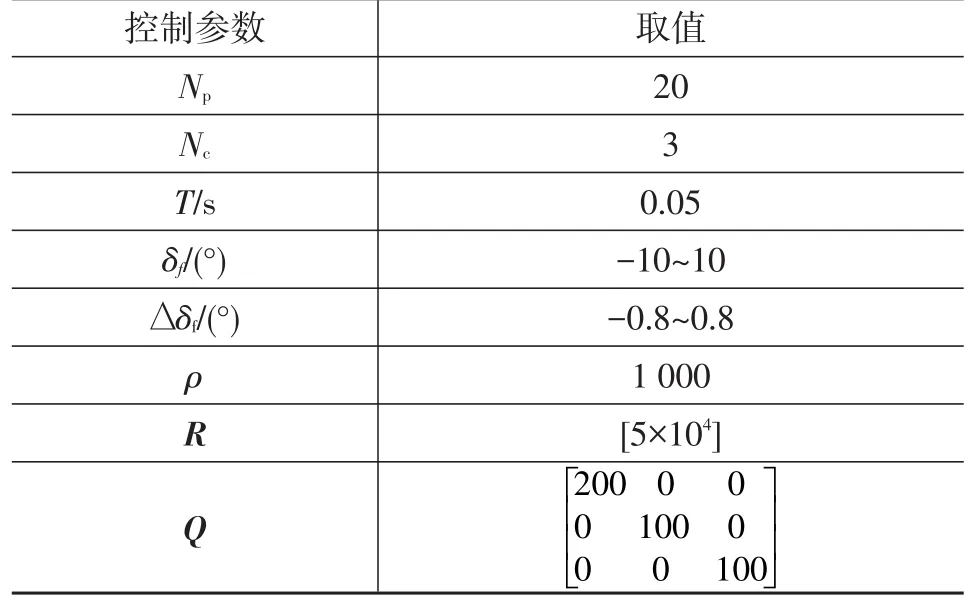
表1 控制器參數

為了驗證本文提出的模型預測控制器在路徑跟蹤上的控制效果，以基于實車參數搭建的3自由度車輛模型作為控制對象，在CarSim平臺和MATLAB/Simulink平臺進行聯合仿真，仿真結果如圖2所示。

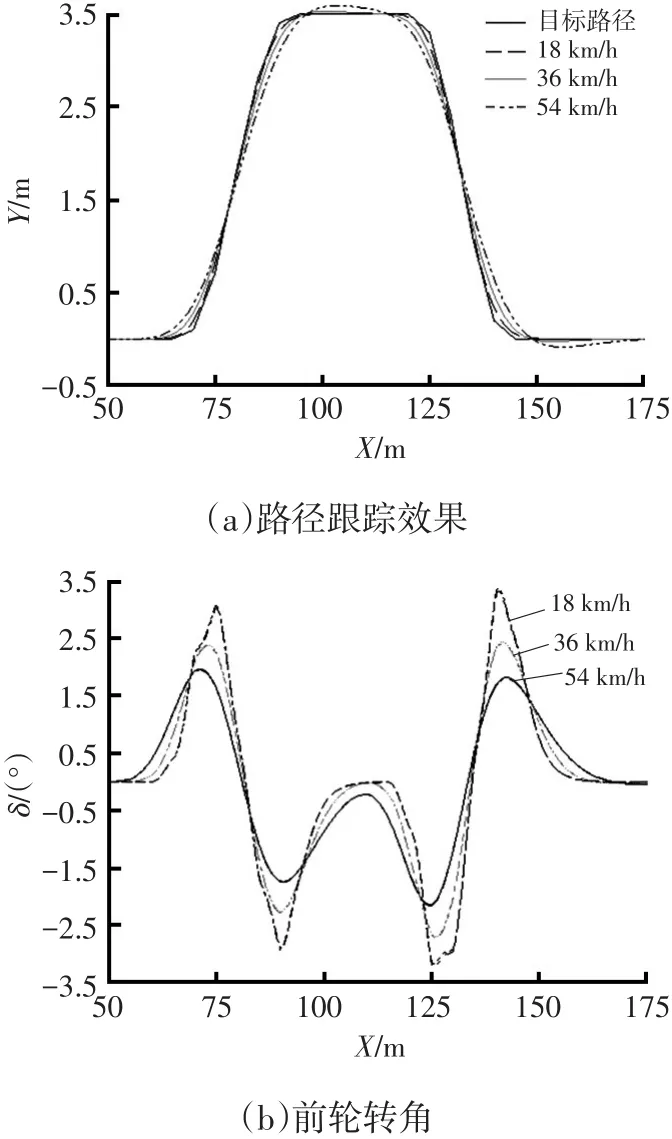
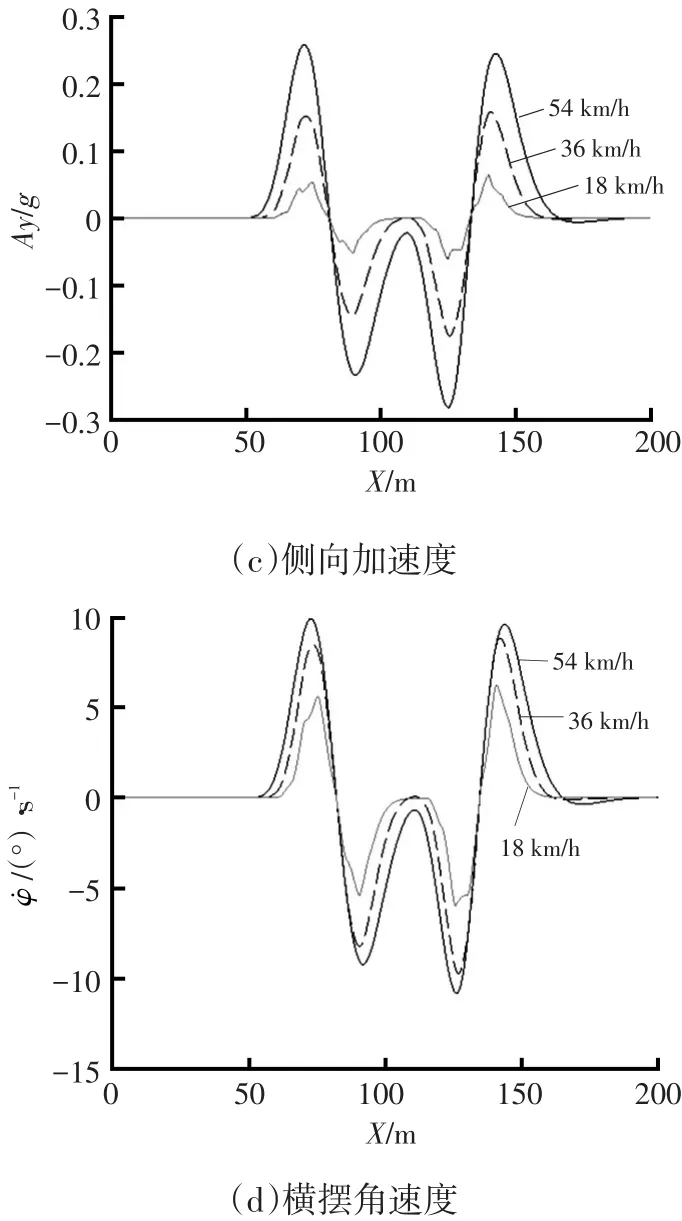
圖2 不同速度下雙移線工況仿真結果

圖2a表明，3種速度工況下車輛都能較好地進行路徑跟蹤，但在彎道處易出現微小偏差，且偏差隨速度的增加而增大，最大偏差為0.1 m，相對于1.87 m的車身寬度可以忽略。

圖2b表明，隨著速度的增加，轉角開始變化的位置前移，由于內、外車輪的行程不同，左、右輪的轉角變化必然存在微小差異。圖2c表明，隨著速度的增加，側向加速度也在增加，但始終保持在±0.3g的較小范圍內。圖2d表明，橫擺角速度變化也很平穩。

由圖2b～圖2d可以看出，前輪轉角、橫擺角速度、側向加速度雖然出現了抖動，但均在較小范圍內，說明該控制器控制下的車輛在運行過程中處于良好的穩定狀態。抖動原因可能是較大的側向加速度使輪胎側偏特性突然處于非線性區，對此，可以考慮適當增加車輛橫擺角的約束，并調整控制器控制時域。

此外，當車輛以18 km/h行駛時，車輛的前輪轉角、側向加速度以及橫擺角速度均對應在彎道處出現抖動，原因可能是車輛低速行駛時幾乎完全跟蹤目標路徑，變化靈敏。

綜上，該控制器的控制效果完全可以滿足中低速情況下智能車輛路徑跟蹤的魯棒性和操縱穩定性要求。

5 結束語

本文針對智能車輛的路徑跟蹤問題，提出了一種基于模型預測控制的路徑跟蹤控制器，搭建了車輛3自由度動力學模型，并在CarSim和MATLAB/Simulink平臺上進行聯合仿真。結果表面，本文所設計的路徑跟蹤控制器可以保障車輛在中低速時具有較好的魯棒性和操縱穩定性，同時滿足乘員對乘坐舒適性的要求。但實際情況下，車輛的速度會高于仿真車速，因此該控制器需要進一步完善，提高其高速行駛下路徑跟蹤的魯棒性和穩定性，這也是本文的后續研究之一。

1 余如.無人駕駛車輛的自動轉向控制：[學位論文].長春：吉林大學，2016.

2 Marino R,Scalzi S,Netto M.Nested PID steering control for lane keeping in autonomous vehicles.Control Engineering Practice，2011，19（12）：1459～1467.

3 姜巖，趙熙俊，龔建偉，等.簡單城市環境下地面無人駕駛系統的設計研究.機械工程學報，2012，48（20）：103～112.

4 孫銀健.基于模型預測控制的無人駕駛車輛軌跡跟蹤控制算法研究：[學位論文].北京：北京理工大學，2015.

5 Macadam C C.Application of an Optimal Preview Control forSimulation ofClosed-Loop Automobile Driving.Systems.IEEE Transactions on Man and Cybernetics，2007，11（6）：393～399.

6 Levinson J,Askeland J,Becker J,et al.Towards fully autonomous driving:Systems and algorithms.IEEE Intelligent Vehicles Symposium，Baden-Baden，2011.

7 張亮修，吳光強，郭曉曉.自主車輛線性時變模型預測路徑跟蹤控制.同濟大學學報，2016，44（10）：1595～1603.

8 陳虹.模型預測控制.北京：科學出版社，2013.

9 龔建偉，姜巖，徐威.無人駕駛車輛模型預測控制.北京：北京理工大學出版社，2014.

10 席裕庚.預測控制.北京：國防工業出版社，1993.

11 余如，郭洪艷，陳虹.自主駕駛車輛的預測避障控制.信息與控制，2015，44（1）：117～124.

（責任編輯 斛 畔）

修改稿收到日期為2017年6月20日。

Design of Intelligent Vehicle Path Tracking Controller Based on Model Predictive Control

Wang Yi,Cai Yingfeng,Chen Long,Wang Hai,Li Jian,Chu Xiaojun
（Jiangsu University,Zhenjiang 212013）

In order to improve the robustness of intelligent vehicle path tracking,this paper proposed a path tracking control method for intelligent vehicle based on model predictive control principle.By linearizing 3-degree-of-freedom nonlinear dynamic model of the vehicle,this method obtained a linear time-varying model and the prediction equation.Next,constraints including the control quantity and the control increment,etc.,were included in the quadratic programming solution process,considering the side slip angle and the road adhesion coefficient which had impact on vehicle handling stability.Finally,co-simulation with different vehicle speeds was carried out under the conditions of double lane change on the CarSim and MATLAB/Simulink platforms.The results show that the controller can realize the path tracking accurately with good stability.

Autonomoussteering,Path tracking,Model predictivecontrol,Intelligent vehicle

自動轉向 路徑跟蹤 模型預測控制 智能車輛

TP242.6 文獻標識碼：A 文章編號：1000-3703（2017）10-0044-05

國家自然科學基金項目（U1564201）。