修正極坐標系下雷達與ESM航跡對準關聯

關欣， 彭彬彬， 衣曉

海軍航空工程學院 電子信息工程系， 煙臺 264001

修正極坐標系下雷達與ESM航跡對準關聯

關欣， 彭彬彬， 衣曉*

海軍航空工程學院 電子信息工程系， 煙臺 264001

研究了存在系統誤差時修正極坐標系(MPC)下的雷達與電子支援措施(ESM)航跡關聯問題。系統誤差導致MPC下雷達和ESM的角度估計產生偏移，而對角度變化率、距變率與距離的比值(ITG)的估計影響不大；結合非中心卡方分布的知識，分析了雷達與ESM的測量誤差對非中心參數和正確關聯概率的影響；提出了一種基于積分重合度的雷達與ESM航跡對準關聯算法。首先將雷達與ESM的目標映射到角度-角度變化率空間，分別得到了雷達與ESM的目標曲線，然后對兩目標曲線求積分重合度，估計出雷達與ESM測角系統誤差的偏移量，對偏移量補償后進行雷達與ESM的航跡關聯。仿真結果表明，本文所提算法能有效地提高存在系統誤差時雷達與ESM正確航跡關聯概率。

系統誤差； 航跡關聯； 雷達； ESM； 非中心參數； 積分重合度； 修正極坐標系

在軍事多傳感器信息融合系統中，異類傳感器的信息融合一直是一個重要又困難的研究課題，其中雷達和電子支援措施(Electronic Support Measurements，ESM)的數據融合就是典型的異類傳感器數據融合問題[1]。雷達和ESM數據融合的前提是雷達和ESM的數據關聯。但是由于ESM是被動傳感器，只能提供角度信息而沒有距離信息，再加上傳感器的誤差和數據率的差異等問題，雷達和ESM航跡關聯存在很大的不確定性[2-3]。文獻[4]研究了在各雷達目標航跡樣本容量不等時雷達與ESM的航跡關聯問題。在此基礎上，文獻[5]簡化了機載雷達與ESM航跡關聯的正確關聯和錯誤關聯概率表達式。上述方法均是利用量測數據構造統計量，為了能更好地利用傳感器提供的信息，文獻[6-7]分別對雷達和ESM量測進行濾波處理后，利用直角坐標系下位置和速度構造關聯統計量，此時為了確保濾波不發散，要求ESM傳感器相對目標進行一定的機動。在修正極坐標系(Modified Polar Coordinates,MPC)下濾波時，當傳感器與目標之間的相對加速度為零時，可觀測的狀態與不可觀測的狀態能自動解耦，確保了穩定跟蹤[8]。文獻[9]在修正極坐標系下對3類典型場景5種關聯方法的正確關聯概率和錯誤關聯概率進行了仿真與分析。文獻[10]在MPC中的前3個狀態向量的基礎上，增加了兩個新的狀態量，基于最大似然估計分析了所提方法的性能。但是上述文獻均未考慮系統誤差的影響[11-13]。

現有的雷達與ESM系統誤差配準方法默認已經實現了航跡關聯，但是由于系統誤差的存在往往無法獲取正確的雷達與ESM航跡關聯關系，從而產生了一個相互為前提的矛盾問題。文獻[14-15]采用圖像匹配的思想，對空間進行網格化劃分，利用傅里葉變換和Randon變換等技術實現了雷達航跡對準關聯。所謂對準關聯，分為航跡對準和航跡關聯兩個步驟，即不依賴準確的系統誤差配準技術下的航跡關聯。然而上述均為雷達組網的情況[16-17]。文獻[18-19]分別研究了系統誤差對基于角度統計量和基于位置統計量的雷達與ESM航跡關聯方法的影響[20]，但是均未提出存在系統誤差時有效的解決方法。

本文對系統誤差存在時MPC下雷達與ESM航跡關聯問題進行了研究，分析了系統誤差對MPC下狀態量的影響。結合非中心卡方分布的知識，分析了雷達與ESM的測量誤差對非中心參數的影響。提出了基于積分重合度的雷達與ESM航跡對準關聯算法，該算法將所有目標看作一個整體，較好地利用了目標間的相對位置信息。不要求對雷達與ESM實現準確的誤差配準，可以估計出雷達與ESM的角度系統誤差間的偏移量，有效地實現系統誤差下雷達與ESM的航跡對準關聯。

1 雷達與ESM的系統方程

假設雷達與ESM位于同一平臺，以平臺中心為坐標原點建立坐標系同時對目標進行定位跟蹤。T為采樣間隔，文中分別記t0T與(t0+k)T時刻為t0和k時刻。平臺在k時刻的位置為(xp(k),yp(k))。假設目標在傳感器的監視區域內勻速直線運動，在直角坐標系的狀態向量為X=[xtvxytvy]T，則k時刻目標相對于平臺的位置可寫為

(1)

式中：x0,y0為目標t0時刻的位置；vx、vy為沿x軸、y軸的速度。雷達量測由距離和方位角組成，且該量測受隨機測量誤差和系統誤差的影響，有

ZA(k)=hX(k)+Δ+Wk

(2)

(3)

(4)

由于ESM只能測得角度信息，所以采用修正極坐標系中對目標進行跟蹤濾波，這可以避免目標與ESM傳感器之間相對加速度為零時直角坐標系中的濾波發散問題[21]。修正極坐標系中目標的狀態向量通常為目標方位角變化率、距離變化率與距離比(Inverse-Time-to-Go，ITG)、方位角和距離的倒數，則ESM的狀態向量表示為

(5)

由于濾波時第4個分量與前面3個分量相互解耦，為了減少計算量只取狀態估計的前面3個項。則其離散狀態下的狀態方程為

(6)

式中：s1=y1(k),s2=y2(k),s3=Ty1(k),s4=1+Ty2(k)。

量測方程為

(7)

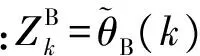
雷達在直角坐標系下的卡爾曼濾波和ESM在MPC下的具體濾波公式可參考文獻[21]。

2 MPC下雷達與ESM航跡關聯

2.1 構造關聯統計量

將雷達在直角坐標系下的狀態估計和協方差轉化到MPC中[11]，前3項狀態估計記為

式中:

(8)

(9)

(10)

在獲得雷達和ESM的目標狀態估計的基礎上，假設PA(k)與PB(k)分別為雷達與ESM在k時刻MPC中的狀態估計的協方差，設

(11)

k時刻第i個雷達航跡與第j個ESM航跡的關聯統計量表示為

(12)

當給定門限λ時，雷達與ESM航跡關聯決策方式為

H0∶η(k)>λ，雷達與ESM航跡不關聯。

H1∶η(k)≤λ，雷達與ESM航跡關聯。

2.2 系統誤差的影響

系統誤差對雷達和ESM航跡關聯統計量的影響以定理的形式給出。

定理對于系統誤差下同地配置的雷達與ESM，MPC中狀態估計的前兩項，即角度變化率和ITG是近似無偏的，而角度估計量由于系統誤差的影響，存在固定偏差；統計量為

證明：k時刻目標位于x(k),y(k)，當雷達與ESM濾波效果良好，雷達目標在MPC的狀態估計為

(13)

(14)

(15)

ESM目標在MPC中的狀態估計為

(16)

(17)

(18)

若雷達航跡與ESM航跡來源于同一個目標，可知

(19)

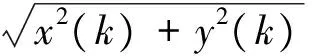
(20)

(21)

式中：雷達與ESM測角系統誤差的偏差c=ΔθA-ΔθB，簡稱為測角系統偏差，通常c并不等于零。系統誤差對狀態向量的前兩項基本不影響，即角度變化率和ITG是近似無偏的，而角度估計由于系統誤差的影響，存在恒定偏差。所以η(k)服從自由度為3、非中心參數為δ(k)的非中心卡方分布：

(22)

式中：

(23)

證畢。

2.3 雷達與ESM測量參數對非中心參數和正確關聯概率的影響

結合式(22)和式(23)，對于系統誤差存在時MPC中的雷達與ESM航跡關聯，提出如下性質：

證明：對于式(23)，顯然隨著c2的增大，非中心參數δ(k)增大；隨著c2的減小，非中心參數δ(k)減小。說明非中心參數不是由雷達或ESM測角系統誤差的具體值，而是由雷達與ESM的測角系統偏差決定的。

然后證明非中心參數與隨機誤差的關系。

雷達目標在直角坐標系下k時刻的Fisher信息陣[10]為

(24)

式中：

(25)

將其由直角坐標轉換到MPC中，可得到雷達目標在MPC中的Fisher信息陣為

(26)

則可以得到雷達目標在MPC中的克拉美-羅下限為

(27)

ESM目標在k時刻的Fisher信息陣為[10]

(28)

ESM目標的克拉美-羅下限為

(29)

(30)

式中：a(n)、b(n)、c(n)、d(n)、e(n)和f(n)為n時刻關于初始狀態X(t0)的函數。這里只是探究雷達與ESM傳感器的誤差對非中心參數的影響，所以并不需寫出確切表達式。

(31)

提取共同的分母：

(32)

式中：

(33)

(34)

可知A(n)和B(n)均為3×3的正定陣。對時間求和后，有

(35)

對于正定陣，加法運算后仍為正定陣，同樣C(k)和D(k)為3×3的正定陣。

同理，對ESM的JB(k)進行類似處理，可以化簡為

(36)

式中：E(k)為3×3的正定陣。所以

(37)

E-1(k)]

(38)

E-1(k)]-1

(39)

證畢。

若給定漏關聯概率，門限為TT即為某個確定常數，得到正確關聯概率為

(40)

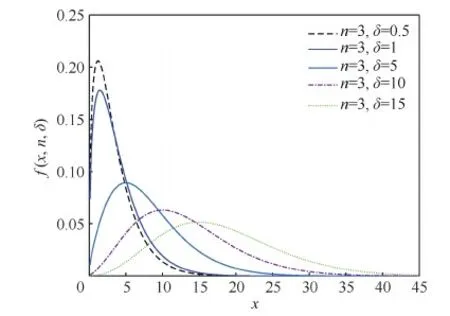
圖1 非中心卡方分布概率密度函數 Fig.1 Probability density function for non-central chi-squared distribution

3 基于積分重合度的雷達與ESM航跡對準關聯算法

第2節討論了系統誤差對MPC下狀態估計量的影響，即系統誤差對前兩個狀態分量基本不影響，只對第3個狀態分量造成固定角度偏移，所以只要能將這個固定的偏移量估計出來，補償后就可以采用現有的關聯算法進行航跡關聯。

(41)

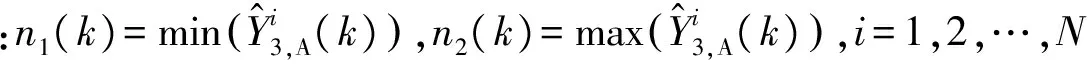
(42)

目標曲線將所有目標視為一個整體，其形狀包含了目標之間的相對位置信息，而與測角系統誤差無關。由于定積分沿著積分軸具有平移不變性，所以以雷達目標曲線為參照，對F2(θ,k)沿著橫軸進行平移，假設平移量為C，得到函數F2(θ+C,k)，則平移后雷達與ESM目標曲線的相似程度用積分重合度S(C,k)可表示為

(43)

式中：u1=min(n1(k),m1(k)+C)，u2=max(n2(k),m2(k)+C)。由于積分上下限含有C，需進行討論，如表1所示。

表1 積分上下限的取值表Table 1 Values for bounds of integral

使得S(C,k)最小的Cmin即為k時刻雷達與ESM測角系統誤差偏差ΔθA-ΔθB的估計值。S(C,k)對C求導，得到S′(C,k)，令S′(C,k)=0，當雷達測角系統誤差大于ESM測角系統誤差時，在區間[n1(k)-m2(k),n2(k)-m1(k)]有唯一解；當ESM測角系統誤差大于雷達測角系統誤差時，在區間[m1(k)-n2(k),m2(k)-n1(k)]存在唯一解。

4 仿真分析

為了驗證本文所提出的基于積分重合度的雷達與ESM航跡對準關聯算法的有效性，在系統誤差存在的情況下對該算法進行仿真實驗。仿真中，正確關聯概率為Pc=Nc/(Nc+Nf+Nm)，錯誤關聯概率為Pf=Nf/(Nc+Nf+Nm)，漏關聯概率為Pm=Nm/(Nc+Nf+Nm)，且有Pc+Pf+Pm=1。其中Nc、Nf和Nm分別為實驗中正確關聯、錯誤關聯和漏關聯點跡對的數目。

4.1 系統誤差影響

假設雷達與ESM位于同一個觀測平臺，平臺初始位置為(0,0) km，以π/2的航向和100 m/s的速度勻速直線運動。存在3個平行直線運動的目標，初始位置分別為(41,31) km、(42,33) km和(39,30) km，航向和速度均為2π/3和200 m/s。雷達與ESM采樣間隔均為1 s，允許的漏關聯概率為0.1。表2為設置的仿真條件，在上述條件下各進行100次蒙特卡羅仿真，對傳統方法[9]在系統誤差存在時進行仿真，并對結果進行分析，圖2 和圖3給出了仿真結果。

表2 系統誤差下雷達與ESM航跡關聯仿真條件Table 2 Simulation conditions of radar and ESM with systematic errors

圖2 系統誤差下雷達與ESM航跡正確關聯概率 Fig.2 Correct association probability of radar and ESM with systematic errors

圖3 系統誤差下目標的狀態估計(σθA=1.0°) Fig.3 Estimates of target with systematic errors (σθA=1.0°)

圖3為實驗2中σθA=1.0° 時某個目標的狀態估計。可以看出存在系統誤差時，修正極坐標系中狀態估計的前兩項，即角度變化率和ITG是近似無偏的，雷達與ESM能穩定跟蹤，說明雷達測距系統誤差對MPC下的ITG估計影響很小；而角度估計由于測角系統誤差的影響，與真實狀態存在固定偏差。

從圖2和圖3中可以看出，當存在系統誤差時，隨著系統誤差的增大，雷達與ESM航跡正確關聯概率減小；隨著雷達或ESM測角誤差的增大，正確關聯概率增大。隨著雷達測距誤差的增大，正確關聯概率增大不明顯。這是因為隨著雷達或ESM測角誤差，關聯統計量的非中心參數減小，導致正確關聯概率增大。不存在系統誤差時，傳統方法[9]的關聯統計量與決策門限均服從卡方分布。存在系統誤差時，門限與關聯統計量不相符，傳統方法不再適用，反常的實驗現象說明了系統誤差下對準雷達與ESM的必要性。

4.2 對準后雷達與ESM航跡關聯性能

在4.1節3個平行運動目標的基礎上，隨機產生3個勻速直線運動目標，目標的速度和初始航向分別在80～120 m/s和0～2π內均勻分布。設置仿真條件如表3所示。

在實驗1的條件下，本文算法與文獻[12]算法分別進行100次蒙特卡羅仿真對比，隨著時間變化的關聯效果如圖4所示。

從圖4中可以看出當存在系統誤差時，隨著時間的推進，由于跟蹤逐漸穩定，本文算法正確關聯概率逐漸提高；基于統計理論的方法未對系統誤差進行對準處理，正確關聯概率不斷下降，即更多的測量數據不僅沒有提高算法的性能，反而導致誤差逐漸積累，影響關聯效果。

表3 雷達與ESM航跡關聯仿真條件Table 3 Simulation conditions of track association of radar and ESM

圖4 關聯概率隨時間變化曲線 Fig.4 Curves of association probability changing over time

為驗證不同誤差下所提算法的有效性，在表3 的條件下，取250～300 s之間的平均關聯性能作為指標，將本文提出的基于積分重合度的雷達與ESM航跡對準關聯算法與未考慮系統誤差的文獻[7]、文獻[9]和考慮系統誤差的文獻[18]算法的關聯性能進行對比，各進行100次蒙特卡羅仿真后結果如表4所示。

圖5分別為280 s時實驗5中對準前與對準后雷達與ESM的目標曲線，即探測到的目標在角度-角度變化率映射空間的分布情況，可以看出，雷達或ESM目標曲線的形狀相似，包含了目標的相對位置信息而與系統誤差無關。存在系統誤差時，如果未對雷達與ESM的測角系統誤差進行估計和對準，雷達與ESM的目標曲線會存在嚴重偏移。從表4中也可以看出，文獻[7]的ESM采用偽線性濾波，屬于有偏估計，存在系統誤差且未對系統誤差進行對準時，文獻[7,9]關聯統計量與所設置的門限不相符，漏關聯概率急劇增加，正確關聯概率迅速下降，且會出現如2.3節所描述的反常現象，無法提供正確的雷達與ESM航跡關聯關系；文獻[18]雖然考慮了系統誤差的影響，但是仍采用傳統的統計方法，對于較大的系統誤差性能并不理想。從圖5(b)中可以看出，本文提出的基于積分重合度的雷達與ESM航跡對準關聯算法首先能較好地估計雷達與ESM的測角系統誤差的差值，對其進行補償后，目標曲線較好地實現對準，算法的漏關聯概率迅速下降，正確關聯概率大幅提高。隨著雷達或ESM的隨機測量誤差增大，算法的正確關聯概率略微下降；對比4.2節中實驗1和實驗7結果可知，在一定范圍內增大雷達的測距系統誤差，正確關聯概率變化不大，結合圖5(a)可知式(21)中的近似處理是合理的；隨著雷達與ESM測角系統誤差的增大或減小，算法始終維持較高正確關聯概率，說明算法對系統誤差存在較好的魯棒性。

表4 雷達與ESM航跡關聯概率Table 4 Track association probability of radar and ESM

圖5 雷達與ESM的目標曲線 Fig.5 Targets curves of radar and ESM

5 結 論

1) 分析了系統誤差對MPC下狀態量的影響，即角度變化率和ITG是近似無偏的，而角度估計量由于系統誤差的影響，與真實狀態存在恒定偏差。

2) 存在系統誤差時，關聯統計量服從非中心卡方分布；理論分析了雷達與ESM的測量誤差對非中心參數和正確關聯概率的影響。

3) 提出了一種基于積分重合度的雷達與ESM航跡對準關聯方法，該方法不需要事先準確地配準雷達和ESM的系統誤差，通過估計和補償雷達與ESM的測角系統誤差相對偏移，正確關聯概率得到大幅提高，解決了傳統方法在有系統誤差性能下降的問題。

[1] 何友, 王國宏, 關欣, 等. 信息融合理論及應用[M]. 北京: 電子工業出版社, 2010: 124-146.

HE Y, WANG G H, GUAN X, et al. Information fusion theory with applications[M]. Beijing: Publishing House of Electronics Industry, 2010: 124-146 (in Chinese).

[2] 韓崇昭, 朱洪艷, 段戰勝, 等. 多元信息融合[M]. 2版. 北京: 清華大學出版社, 2010: 455-496.

HAN C Z, ZHU H Y, DUAN Z S, et al. Multi-source information fusion[M]. 2nd ed. Beijing: Tsinghua University Press, 2010: 455-496 (in Chinese).

[3] 趙宗貴, 刁聯旺, 李君靈, 等. 信息融合工程實踐——技術與方法[M]. 北京: 國防工業出版社, 2014: 50-75.

ZHAO Z G, DIAO L W, LI J L, et al. Information fusion engineering practice—Technology and method[M]. Beijing: National Defence Industry Press, 2014: 50-75 (in Chinese).

[4] WANG G H, MAO S Y, HE Y. Triple-threshold radar to ESM correlation algorithm when each radar track is specified by different number of measurements[J]. IEE Proceedings-Radar, Sonar and Navigation, 2000, 147(4): 177-187.

[5] WANG G H, MAO S Y, HE Y. Analytical performance evaluation of association of active and passive tracks for airborne sensors[J]. Signal Processing, 2003, 83(5): 973-981.

[6] CHEN H, BAR-SHALOM Y. Track association and fusion with heterogeneous local trackers[C]//The 46th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 2007: 12-14.

[7] WANG G H, ZHANG X Y, TAN S C. Effect of biased estimation on radar-to-ESM track association[J]. Journey of System Engineering and Electronic Techniques, 2012, 23(2): 188-194.

[8] 孫仲康, 郭福成, 馮道旺. 單站無源定位跟蹤技術[M]. 北京: 國防工業出版社, 2008: 150-160.

SUN Z K, GUO F C, FENG D W. Passive location and tracking technology by single observer[M]. Beijing: National Defense Industry Press, 2008: 150-160 (in Chinese).

[9] BENAMEUR K. Radar ESM track to track association: DREO-TR-2001-115[R]. Ottawa: Defence Research Establishment Ottawa, 2001.

[10] ZHOU Y F, LI W, LEUNG H. Maximum likelihood based ESM/radar track association algorithm in a new modified polar coordinate: DRDC-Ottawa-TM-2004-255[R]. Ottawa: Defence Research and Development Canada, 2004.

[11] SCALA B F L, FARINA A. Choosing a track association method[J]. Information Fusion, 2002, 3(2): 119-133.

[12] OFFER C R. Performance of bearing-only ESM-radar tracking association[C]//IET Data Fusion & Target Tracking Conferrence. London: IET, 2012.

[13] SCALA B F L, FARINA A. Effects of cross-covariance and resolution on track association[C]//Proceedings of the 3rd International Conference on Information Fusion. Piscataway, NJ: IEEE Press, 2000.

[14] 何友, 宋強, 熊偉. 基于傅里葉變換的航跡對準關聯算法[J]. 航空學報, 2010, 31(2): 356-361.

HE Y, SONG Q, XIONG W. A track registration correlation algorithm based on Fourier transform[J]. Acta Aeronoutica et Astronautica Sinica, 2010, 31(2): 356-361 (in Chinese).

[15] 何友, 宋強, 熊偉. 基于相位相關的航跡對準關聯技術[J]. 電子學報, 2010, 38(12): 2718-2723.

HE Y, SONG Q, XIONG W. Track alignment-orrelation technique based on phase correlation[J]. Acta Electronica Sinica, 2010, 38(12): 2718-2723 (in Chinese).

[16] 吳澤民, 任姝婕, 劉熹. 基于拓撲序列法的航跡關聯算法[J]. 航空學報, 2009, 30(10): 1937-1942.

WU Z M, REN S J, LIU X. Topology sequence based track correlation algorithm[J]. Acta Aeronoutica et Astronautica Sinica, 2009, 30(10): 1937-1942 (in Chinese).

[17] 石玥, 王鉞, 王樹剛, 等. 基于目標參照拓撲的模糊航跡關聯方法[J]. 國防科技大學學報, 2006, 28(4): 105-109.

SHI Y, WANG Y, WANG S G, et al . Fuzzy data association based on target topology of reference[J]. Journal of National University of Defense Technology, 2006, 28(4):105-109 (in Chinese).

[18] 宋振宇, 張翔宇, 張光軼. 系統誤差對異地配置的雷達和ESM航跡關聯的影響[J]. 電光與控制, 2014, 21(3): 42-46.

SONG Z Y, ZHANG X Y, ZHANG G Y. Effect of systematic errors on radar-to-ESM track association at different sites[J]. Electronics Optics & Control, 2014, 21(3): 42-46 (in Chinese).

[19] 張翔宇, 王國宏, 王娜, 等. 系統誤差下異地配置的雷達和電子支援測量航跡關聯[J]. 電光與控制, 2012, 19(3): 30-34.

ZHANG X Y, WANG G H, WANG N, et al. Track association of radar and ESM sensors with systematic errors at different sites[J]. Electronics Optics & Control, 2012, 19(3): 30-34 (in Chinese).

[20] 關欣， 孫貴東， 衣曉, 等. 基于關聯系數靶心距的混合多屬性識別研究[J]. 航空學報, 2015, 36(7): 2431-2443.

GUAN X, SUN G D, YI X, et al. Research on hybrid multiple attribute recognition based on coefficient of incidence Bull’s-eye-distance[J]. Acta Aeronoutica et Astronautica Sinica, 2015, 36(7): 2431-2443 (in Chinese).

[21] 何友, 修建娟, 張晶煒, 等. 雷達數據處理及應用[M]. 北京: 電子工業出版社, 2009.

HE Y, XIU J J, ZHANG J W, et al. Radar data processing with applications[M]. Beijing: Publishing House of Electronics Industry, 2009 (in Chinese).

(責任編輯： 蘇磊)

URL：www.cnki.net/kcms/detail/11.1929.V.20161110.0829.002.html

Trackalignment-associationofradarandESMinMPC

GUANXin，PENGBinbin，YIXiao*

DepartmentofElectronicsandInformationEngineering,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China

Thispaperconductsresearchontheproblemoftrackassociationofradarandelectronicsupportmeasurements(ESM)withsystematicerrorsexistinginmodifiedpolarcoordinates(MPC).SystematicerrorscancauseamassmotionofbearingestimatesofradarandESMinMPC,butonlyslightinfluenceontheestimateofbearingrateandinverse-time-to-go(ITG).Byreferringtoknowledgeofnon-centralchi-squareddistribution,theeffectofmeasurementerrorsofradarandESMonnon-centralparametersandprobabilityofcorrectassociationareanalyzed.Atrackalignment-associationalgorithmforradarandESMbasedonoverlapratioofintegralisproposed.ThetracksofradarandESMaremappedintothebearing-bearingratespacetogainthecurvesofradarandESM.Then,theoverlapratioofintegralofthetargetcurvesiscalculated,andthemassofbearingsystematicerrorsofradarandESMisestimated.Thetrackassociationisachievedafterthemassiscompensated.Simulationresultsshowthatprobabilityofcorrectassociationcanbeimprovedeffectivelybytheproposedalgorithminthepresenceofsystematicerrors.

systematicerror;trackassociation;radar;electronicsupportmeasurements;non-centralparameter;overlapratioofintegral;modifiedpolarcoordinates

2016-08-08；Revised2016-09-21；Accepted2016-11-04；Publishedonline2016-11-100829

s：NationalNaturalScienceFoundationofChina(61032001);ProgramforNewCenturyExcellentTalentsinUniversityofMinistryofEducationofChina(NCET-11-0872)

.E-mailyxgx_gxyx@163.com

2016-08-08；退修日期2016-09-21；錄用日期2016-11-04； < class="emphasis_bold">網絡出版時間

時間：2016-11-100829

www.cnki.net/kcms/detail/11.1929.V.20161110.0829.002.html

國家自然科學基金 (61032001)； 教育部新世紀優秀人才支持計劃 (NCET-11-0872)

.E-mailyxgx_gxyx@163.com

關欣， 彭彬彬， 衣曉． 修正極坐標系下雷達與ESM航跡對準關聯J． 航空學報,2017,38(5):320668.GUANX,PENGBB,YIX.Trackalignment-associationofradarandESMinMPCJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):320668.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0287

V243.2;TN958

A

1000-6893(2017)05-320668-12