星敏感器低頻誤差與陀螺漂移離線校正方法

趙琳， 謝睿達， 劉源， 郝勇

哈爾濱工程大學 自動化學院， 哈爾濱 150001

星敏感器低頻誤差與陀螺漂移離線校正方法

趙琳， 謝睿達*， 劉源， 郝勇

哈爾濱工程大學 自動化學院， 哈爾濱 150001

獲取高精度事后姿態數據是提高遙感平臺成像質量的必要條件之一，離線處理可有效降低敏感器測量誤差，從而獲得更高的姿態確定精度。基于濾波的校正方法中，星敏感器低頻誤差(LFE)與陀螺漂移將產生耦合影響導致校正精度低，本文針對該問題推導了耦合誤差的數學模型，并設計了一種兩步雙向平滑事后處理算法，將陀螺漂移與低頻誤差分兩步校正，通過反復濾波剝離陀螺漂移與低頻誤差。同時，針對低頻誤差參數收斂速度慢、噪聲參數調節困難的問題，利用一種基于極大似然估計(MLE)的固定窗口自適應雙向濾波算法進行處理以獲得更好的噪聲估計，提高了收斂速度和收斂精度。文中仿真工況下，離線姿態確定精度可達到0.8″(3σ)，低頻誤差參數完全收斂時間不超過4個軌道周期。

星敏感器； 低頻噪聲； 陀螺漂移； 衛星姿態測量； 事后處理； 姿態敏感器誤差標定

現代對地觀測衛星中，姿態確定精度直接影響遙感圖像處理質量，而事后姿態處理往往可獲得較高的姿態確定精度，因此能夠高精度地進行事后姿態確定對遙感衛星至關重要。以先進對地觀測衛星(Advanced Land Observing Satellite， ALOS)為例：精確指向與地理定位系統(Precision Pointing and geolocation Determination System,PPDS)是ALOS的地面子系統之一，由于不存在在軌計算量、實時性等約束，其可以實現高精度的衛星姿態與指向修正。根據現有資料[1-2]，其地球觀測中心(Earth Observation Center，EOC)可下載至少24 h的低速任務數據及來自跟蹤與控制中心(Tracking And Control Center，TACC)的定位數據。PPDS主要實現以下功能：星敏感器誤差校正、事后姿態處理、熱變形建模與估計等。ALOS的典型在軌精度為(±3×10-4)°(3σ)，而通過事后處理，其姿態精度可提高一倍以上，為(±1.4×10-4)°(3σ)，此外，指向精度、穩定度經事后處理均有提升。

諸多學者對衛星姿態的事后處理進行了研究，主要研究對象包括衛星姿態敏感器誤差的事后補償和衛星姿態數據后處理等。事后處理主要是利用了處理時可以利用全部時間的測量數據、計算量不受限制等特性。Iwata等[3-5]針對ALOS數據事后處理進行了較全面的闡述，其主要通過對陀螺漂移的補償和星敏感器星圖再處理提高姿態精度。Lei和Yang[6]利用RTS(Rauch-Tung-Striebel)算法處理擴展卡爾曼濾波(EKF)姿態算法的數據。Yang和Lei[7]參考了Sarkka的部分成果[8]研究了利用無跡卡爾曼濾波(UKF)姿態確定算法配合RTS算法，形成URTS固定區間平滑算法，但未考慮敏感器誤差補償，僅對事后姿態數據進行了RTS處理，其處理精度低于Iwata的處理精度[4]。以上學者主要是針對濾波中的姿態誤差或陀螺漂移進行平滑處理，但沒有考慮到星敏感器低頻誤差(LFE)帶來的影響。

星敏感器是星上精度最高的敏感器，但由于受到歲差、章動、低頻誤差等影響，其精度會受到很大影響，其中低頻誤差分量可達到十幾至幾十角秒，且該誤差難以在軌消除，一般通過事后處理方可消除[9]。針對低頻誤差，熊凱等在文獻[10]中提出的在軌校準方法精度有限；在文獻[11]中提出的一種基于多模型自適應估計的算法，估計效果較好，但該算法理解性差，濾波參數調節復雜；在文獻[12]中提出的基于地標信息的方法受到地標信息不準確、載荷誤差的影響，校正精度有限。Schmidt等[13]提出用多項式擬合星敏感器四元數來提取低頻誤差，但受多項式精度限制，簡單擬合效果不理想。Lai等對實驗四號衛星安裝的Astro10星敏感器進行系統校正，利用Vondrak濾波的方法進行處理，取得了較好的效果[14-15]。文獻[16]分別討論了星敏感器和陀螺的在軌標定，但沒有對低頻誤差和陀螺漂移之間的耦合影響進行分析。綜上，以上文獻基本利用了濾波的方法對低頻誤差進行校正，但均沒有考慮陀螺漂移與低頻誤差校正間的相互影響，且對濾波器的性能研究不深入。本文針對以上不足探討以下內容：對濾波過程中低頻誤差參數與陀螺漂移間的耦合影響進行了推導，給出了具體的數學表達和分析；設計了一種兩步雙向平滑算法，剝離低頻誤差與陀螺漂移誤差；針對低頻誤差參數在濾波中調參難、收斂難的問題，提出一種基于極大似然估計(MLE)固定時間窗口的雙向自適應平滑算法。

1 低頻誤差參數與陀螺漂移估計過程分析

1.1 低頻誤差建模

低頻誤差的成因較多，根據文獻[9,17-18]，低頻誤差是由星敏感器光軸指向的周期性變化造成的，其中指向變化是由周期性的熱彈性形變結合熱滯后效應形成的。低頻誤差基本是以軌道周期呈現的規律未知的誤差，根據文獻[10-12,19]，本文采用傅里葉級數對低頻誤差輪廓進行描述(如式(1)所示)，利用傅里葉級數一方面可以有效擬合低頻誤差，另一方面低頻成分可控，便于評價算法效能。

(1)

式中：Θx為x軸低頻誤差；a、b為傅里葉系數；ωorbit為軌道角速度；i為信號為軌道周期的若干倍頻；k為仿真步數；τ為仿真步長。

低頻誤差體現在星敏感器坐標系下，通過式(2)轉換至衛星本體系下。

(2)

1.2 低頻誤差與陀螺漂移影響分析

對于基于濾波的方法，需要對估計過程中可能產生的影響因素加以分析。低頻誤差參數估計過程中，由于星敏感器本身帶有低頻誤差，因此利用該信息為基準不能剝離出誤差參數；而陀螺信息與低頻誤差參數是不相關的，因此可以用陀螺信息作為基準。本節參考文獻[19]的思路，對同時估計和分別估計陀螺漂移和低頻參數時，二者間的相互影響進行了數學分析。

若狀態量選取為X=[δqδbδκ]T，δq為四元數偏差，δb為漂移，δκ為低頻參數，且

(3)

狀態量選取為估計值與真實值之間的偏差，則非線性系統在線性化、離散化過程后，可建立如式(4)所示的狀態方程與觀測方程。

(4)

式中：Qk為系統噪聲；Rk為量測噪聲；且

(5)

(6)

(7)

其中：ci,k，si,k(i=1,2,…,n)為傅里葉級數的余弦和正弦分量。

假定新息序列υk與預測殘差ρk為小量，則有

(8)

且有

δqk-δqk/k-1=ρk

(9)

由觀測方程得

Zk=HkXk+Rk=δqk+φkδκk+Rk

(10)

同時，由式(8)得

(11)

將式(8)中的Zk代入式(10)，得

(12)

由狀態方程得

(13)

將式(9)和式(12)中的k時刻推進至k+1，并代入式(13)，得

(14)

為了得到低頻誤差參數與陀螺漂移之間的關系，應盡量將四元數消除，由狀態方程得

(15)

將式(15)和式(12)代入式(14)，消除帶四元數的項，并分別將低頻誤差參數與陀螺漂移整理至等式右側，得

Qq,k-Qq,k-1-υk+Rk-ρk}

(16)

Qq,k+υk+1-Rk+1+ρk+1}

(17)

式(16)右側第2項代表了陀螺漂移估計偏差對低頻誤差參數估計的影響，第3項代表其受到前一時刻低頻誤差參數估計不準確的影響，第4項則為與衛星機動有關的誤差項；式(17)中也可明顯分析出陀螺漂移估計受到低頻誤差影響。

Qq,k+1+Qq,k+υk+1-Rk+1+ρk+1]

(18)

由式(18)可以看出，低頻誤差將直接影響陀螺漂移，右側第2項為低頻誤差變化帶來的影響，第3項為與衛星機動角速度相關的誤差分量。

由式(8)得

(19)

在濾波器內部，觀測量由式(20)計算。

(20)

(21)

將式(21)代入式(20)，得

(22)

與式(8)對照，可得

υk=δq? b,k/k-1+δqo

(23)

由式(23)可得陀螺漂移對低頻誤差分量估計的影響如式(24)所示。

Qq,k+1-Qq,k+Rk+1-ρk+1}

(24)

式(24)中，第4項、第5項中的υk和υk+1分別代表了未校準的陀螺漂移殘差對低頻誤差估計的影響，第4項與衛星機動相關，第5項則與低頻誤差各階分量的幅值有關。

由上述推導可得，低頻誤差參數估計與陀螺漂移估計是兩個相互影響的過程，將二者分開估計或同時估計都會造成估計不準確。但是，分開估計較同時估計更為合理。首先，低頻誤差規律以軌道為周期，因此參數至少需要一軌甚至多軌的時間才能得到較好的收斂，但陀螺漂移估計收斂則較為迅速，一旦存在星敏感器信息，即可在較短時間內收斂。其次，陀螺漂移事后處理可通過反復平滑獲得均方差較小的估計值，而低頻誤差參數則僅需要一次平滑處理即可，因此同時估計將造成極大的不方便。最后，低頻誤差參數會使狀態量成倍遞增，且部分高階參數相對于陀螺漂移估計量級較低，濾波過程中漂移誤差對其造成的影響較大，甚至出現發散的現象。綜上，設計合適的策略將二者分開估計更有優勢。

2 低頻誤差與陀螺漂移離線高精度校正

2.1 算法流程概述

低頻誤差與陀螺漂移分兩步校正的算法流程如圖1所示。用本文所提出的低頻誤差與陀螺漂移高精度事后校正方法獲得陀螺與星敏感器原始數據后，首先不考慮低頻誤差進行反復平滑漂移估計，此階段需進行多次平滑獲得漂移估計值；而后利用經過校正的角速度測量數據與星敏感器原始數據進行低頻誤差參數估計，此階段只需要一次平滑以獲得收斂精度較高的估計值。上述過程重復多次，直至獲得較好的誤差估計，即頻域上陀螺漂移估計與星敏感器輸出均不含有低頻分量。需要注意的是，為了保證足夠的低頻誤差輪廓以獲得低頻誤差參數估計值，在每輪循環的低頻參數估計階段均使用星敏感器輸出的原始數據；同理為使陀螺漂移估計盡量小地受低頻參數的影響，在陀螺漂移估計過程中使用的是上一輪循環校正過的星敏感器姿態數據。

圖1 低頻誤差與陀螺漂移離線估計方法 Fig.1 Offline estimation method of low frequency error (LFE) and gyroscope drift

2.2 基于固定區間平滑的陀螺漂移精準估計算法

平滑是衛星數據事后處理的基本思想[3]，本節將對陀螺漂移平滑過程進行推導。

1) 前向濾波

首先利用姿態運動學進行預測：

(25)

(26)

2) 后向濾波

后向濾波過程與前向濾波類似，將下標f替換為b，前向濾波通過k-1時刻預測k時刻值，后向濾波則利用k+1時刻預測k時刻值，相應公式按照該思路進行修改。

前向濾波狀態量X初值一般取0，即姿態與陀螺漂移估計初始時刻為零，噪聲協方差陣P按照經驗設定初值，因此需要一定時間達到收斂狀態，而后向濾波初值則取前向濾波終值，即

(27)

因此后向濾波狀態量X及噪聲協方差陣P在后向濾波初始時刻均有較高質量的估計。

3) 權值融合

(28)

式中：

(29)

同時，可以求得前后向漂移估計差為

(30)

則前后向濾波產生的狀態量誤差可表示為

(31)

平滑后的均方誤差為

(32)

(33)

令

(34)

則利用平滑四元數偏差對后向姿態估計進行修正：

(35)

平滑后的陀螺常值漂移：

(36)

平滑后得到的陀螺漂移用于補償當前三軸角速度并用于下一次平滑，平滑得到的最終漂移則補償低頻誤差階段使用的三軸角速度數據。

2.3 基于MLE自適應雙向濾波的低頻誤差離線校正算法

1) 低頻誤差與陀螺漂移先驗補償

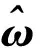
2) 自適應雙向卡爾曼濾波平滑

前向卡爾曼濾波過程與陀螺平滑過程運算相類似，不同之處在于，濾波狀態量擴展為

(37)

則觀測矩陣為

(38)

為取得良好的收斂效果，在原有EKF的觀測量中需剔除估計的低頻誤差分量：

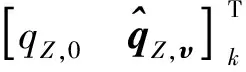
(39)

(40)

式中：Κ為歐拉角姿態轉換為四元數姿態的轉換矩陣。在仿真研究中發現，由于低頻誤差的噪聲特性是未知的，且參數量級相差大，在濾波的過程中，噪聲參數調節復雜，經常出現激勵不當導致的發散現象。因此推導一種基于更新序列殘差的MLE自適應雙向濾波方法，以提高收斂時間和收斂精度。

推導前有以下假設：

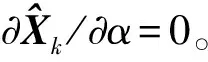
假設2狀態轉移矩陣Φ及觀測矩陣H獨立于α，即?Hk/?α=0，?Φk/?α=0。

假設3更新殘差序列為白噪聲序列。

假設4更新殘差序列是與α相關的變量，即?ΡδXk/?α≠0。

在k時刻，與自適應變量α相關的測量概率密度函數為[12]

(41)

式中：m為測量值的數量；Pγk為殘差序列的協方差矩陣；γk為殘差序列。本文中，自適應參數α為噪聲方差矩陣的對角線元素，如:αi=Rii或αi=Qii。為方便推導，對式(41)兩邊同時取對數，并同時乘以-2，則MLE過程中求取Ρ的最大解變為求解式(42)右側的最小值。

(42)

考慮到內存、運算量及新的姿態測量更新數據的比重問題，即使是在事后運算中，也不必取全部時間的數據進行運算，因此采用開窗法，采用時間長度為N的觀測窗口進行計算，因此MLE準則有如式(43)所示的形式。

(43)

式中：p為當前時刻。

對式(43)兩邊分別求取參數α的偏導數，通過變換有

(44)

由式(44)可知，MLE自適應濾波中需要調整的參數項為α和殘差序列γk，但這兩個參數的調整較為抽象，因此要將這兩個變量與調整系統噪聲Q與星敏量測噪聲R聯系起來。以下進行推導。

已知[20]

(45)

且有

(46)

將式(46)代入式(45)，并求偏導，得

(47)

認為選定的觀測k窗口長度可以使低頻誤差參數與四元數矢量部分達到穩定，因此狀態轉移矩陣相關的影響為零，因此有

(48)

將式(48)代入式(44)中，推導出如式(49)所示的基于更新殘差序列的MLE自適應濾波參數調整準則。

(49)

當只對R進行調節時，假設Q為無關向量，即?Qk/?α=0，那么取αi=Rii，則有

(50)

利用式(51)求測量噪聲替代固定值。

(51)

(52)

Qk=ΡδXk+Pk-ΦPk-1ΦT

(53)

其中：

(54)

δXk=Kkυk

(55)

其中：Kk為卡爾曼增益矩陣。式(37)～式(55)即基于MLE的前向自適應濾波參數調整流程。由于噪聲估計準確，因此算法運行效率高、收斂性好。

值得注意的是，由于后向濾波初值即采用前向濾波終值，因此后向濾波不需要該自適應方法進行調節。

3 基于噪聲方差陣的權值融合

將式(31)前后向狀態估計誤差修改為

(56)

得到平滑補償信息后，姿態四元數仍按照式(35)補償，低頻誤差按照式(57)進行估計。

(57)

與陀螺漂移反復平滑不同，低頻誤差參數估計僅進行一次融合獲得更精確的收斂值，而非將反復平滑的結果疊加，其目的是要在陀螺漂移估計階段消除星敏感器低頻誤差的影響，直至陀螺漂移與低頻誤差能夠準確地剝離。

4 仿真結果

衛星軌道周期為90 min，陀螺信息輸出頻率為4 Hz，三軸常值漂移分別設置為[0.8 1.0 1.2]T(°)/h，常值漂移噪聲均方差為0.02 (°)/h；相關漂移初值為[0.1 0.1 0.1]T(°)/h，相關漂移噪聲均方差為0.1 (°)/h，相關時間常數為1 h，隨機噪聲為0.01 (°)/h，星敏感器輸出頻率為1 Hz，低頻參數值的選取基于某遙感衛星星敏感器測量數據提取的低頻輪廓，針對該組參數，信噪比設置為95，其他影響誤差以0.1″(3σ)的白噪聲代替。

陀螺測量數據按照式(58)所示的測量模型產生。

ωm=ω+b+d+ηg

(58)

式中：ωm與ω分別為陀螺測量值及衛星三軸真實角速度；b為常值漂移；d為時間相關漂移；ηg為陀螺測量隨機噪聲，假設為均勻分布的高斯白噪聲。本文在陀螺建模階段，沒有考慮陀螺在軌運行時的周期性漂移。由于本文將陀螺漂移與低頻誤差分別迭代計算，因此即使陀螺存在周期性漂移，本文所提出的算法仍然能夠將陀螺周期性誤差與低頻誤差分離。

圖2為含低頻誤差的星敏感器輸出曲線，圖3 為不考慮低頻誤差的陀螺漂移估計頻譜。由圖2 和圖3可以看出，當不考慮低頻誤差時，漂移估計中存在幅值較大的低頻誤差，使得陀螺漂移估計具有較大的均方差，該仿真結果驗證了本文式(18)得出的結論：不考慮低頻誤差時，低頻誤差對陀螺漂移估計造成較大影響。

圖4給出了未考慮陀螺漂移殘差時1階、5階傅里葉參數估計的情況。如圖4所示，1階傅里葉參數雖然收斂，但由于陀螺漂移殘差的影響，其仍然有振蕩的趨勢，5階傅里葉參數量級較小，因而圖4(b)中這種振蕩體現得較為明顯。

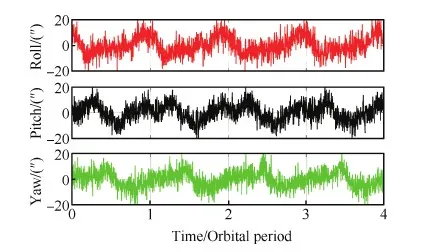
圖2 含低頻誤差的星敏感器輸出 Fig.2 Star sensor output with LFE

圖3 未考慮星敏感器低頻誤差的陀螺漂移估計頻譜 Fig.3 Spectrum of gyroscope drift estimation without considering star sensor LFE

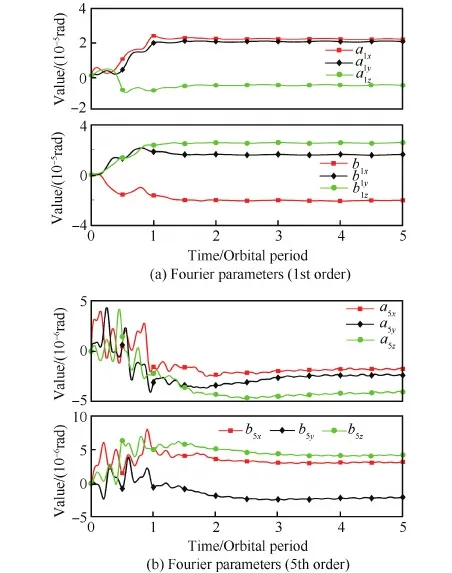
圖4 未考慮陀螺漂移的低頻誤差參數估計 Fig.4 LFE parameter estimation without considering gyroscope drift

根據上述參數估計對星敏感器進行校正時，獲得如圖5所示的校正結果,校正殘差幅值約為2″，低頻誤差未得到很好的校正，由圖5(b)可以看出，三軸姿態頻譜中，低頻誤差分量雖然得到抑制，但未能消除。以上仿真結果驗證了式(24)中陀螺漂移殘差將影響低頻誤差估計的結論。

文獻[10]提出將低頻誤差參數與陀螺漂移一同估計，本文對該方法進行了仿真分析，評價估計效果時取第8～10軌達到穩態時的數據進行分析。如圖6所示，將低頻誤差參數與陀螺漂移一同估計時，由于對陀螺漂移一同進行了估計，因此收斂效果優于單獨估計低頻誤差的情況，但參數收斂后仍有振蕩，且參數收斂周期較長。

圖7為同時估計漂移和低頻誤差時的衛星姿態估計結果。如圖7(a)所示，隨著低頻誤差參數與陀螺漂移估計參數的逐漸收斂，姿態確定誤差越來越小，但如圖7(b)所示，即使達到算法收斂的狀態，任然無法消除全部低頻誤差，姿態信息中仍有以軌道周期或其倍頻分量為周期的較大的低頻誤差。

圖5 僅考慮低頻誤差時衛星三軸姿態的校正結果 Fig.5 Results of satellite 3-axis attitude calibration considering only LFE

圖6 同時估計陀螺漂移和低頻誤差參數時的低頻誤差估計結果 Fig.6 LFE estimation results when gyroscope drift and LFE parameters are estimated simultaneously

如圖8所示，由于低頻誤差參數與陀螺漂移一同估計，而低頻參數收斂時間長，導致陀螺漂移收斂時間長，且陀螺在初始階段振蕩劇烈，振蕩幅值達到了±3 (°)/h，且收斂后頻譜分析顯示，仍有幅值約為0.01 (°)/h的低頻誤差殘余，校正精度有限。

上述仿真結果證明了式(3)～式(17)數學分析的正確性，即一同估計誤差將會降低估計精度，且會導致陀螺收斂周期變長。仿真數值結果如表1 和表2所示。

圖7 同時估計陀螺漂移和低頻誤差參數時衛星姿態的估計結果 Fig.7 Satellite attitude estimation results when gyroscope drift and LFE parameters are estimated simultaneously

圖8 同時估計陀螺漂移和低頻誤差參數時的陀螺漂移估計結果 Fig.8 Gyroscope drift estimation results when gyroscope drift and LFE parameters are estimated simultaneously

表1 同時估計陀螺漂移與低頻誤差時的校正結果Table 1 Calibration results when gyroscope drift and LFE are estimated simultaneously

ParameterRollPitchYawRMSofgyroscopedrift/((°)·h-1)0．807171．047761．23154RMSEofgyroscopedrift/((°)·h-1)0．092490．104660．10641Standardderivationofgyroscopedrift/((°)·h-1)0．507990．653940．86160Precisionofcalibratedstarsensor/(″)(3σ)1．943841．968591．98642Standardderivationstarsensorerror/(″)0．652610．654470．65297Precisionofofflineattitudedetermination/(″)(3σ)1．178421．170771．16670

Notes: RMS——Root Mean Square; RMSE——Root Mean Square Error.

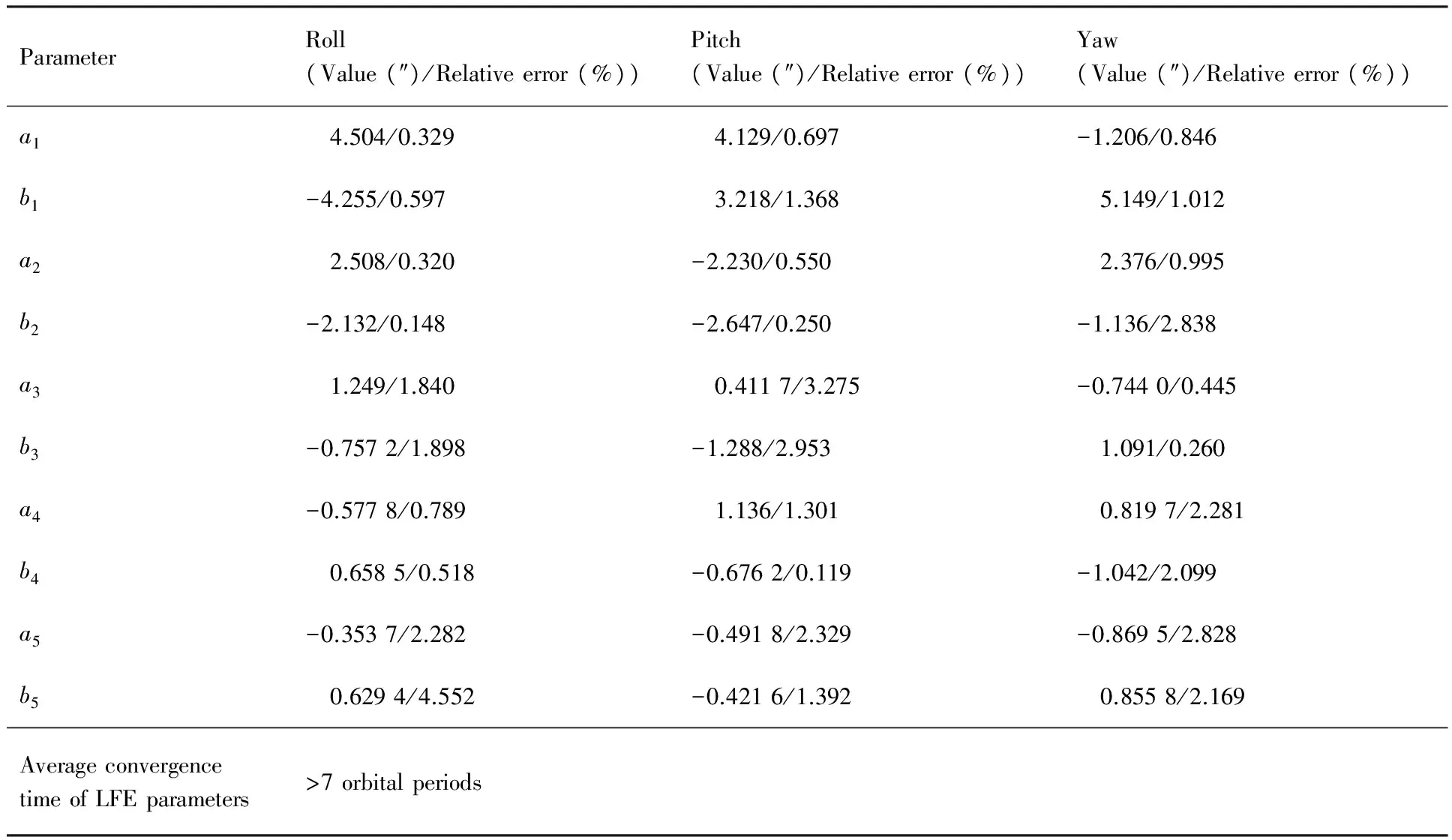
表2 陀螺漂移與低頻誤差同時估計時低頻誤差參數的估計結果Table 2 LFE parameter estimation results when gyroscope drift and LFE are estimated simultaneously

如表1所示，原有估計方法得到的陀螺漂移均方根誤差(RMSE)的量級約為0.1 (°)/h，星敏校正精度約為2″，綜合處理精度在1.17″左右，由表2可知，參數收斂時間超過7個軌道周期，且參數估計不穩定，部分低階誤差參數估計出現了較大偏差。針對上述情況，應用本文第2節提出的離線處理算法，進行仿真驗證，圖9和圖10為仿真結果。

如圖9所示，第1次循環處理中，經過反復平滑，三軸陀螺漂移誤差均方差明顯降低，但由于低頻誤差影響，明顯可觀察其存在周期性誤差。由圖9(b)和圖9(c)可知，低頻誤差存在于陀螺漂移估計與校正后的星敏感器數據中。

如圖10所示，經過3次循環，陀螺漂移已去除趨勢項，通過分析其頻譜也可以看出陀螺漂移與星敏數據低頻誤差影響基本被校正。

表3和表4給出了圖9和圖10所示結果的具體數值結果，表3所示為本文所提基于雙向濾波的兩步法的具體仿真結果，對循環過程中的每一次的陀螺漂移、星敏感器校正及姿態確定精度及殘差的離散程度進行了評估，表4為運用該算法得到的低頻誤差參數值的最終仿真結果。仿真過程中，陀螺漂移估計平滑次數設定為3，低頻參數平滑次數設定為1，整體循環估計次數在第3次循環滿足條件。

由表3所示，經過3次校正后，陀螺漂移估計標準差與星敏感器校正殘差標準差明顯降低，分別由[0.114 7 0.116 3 0.141 8] (°)/h和[5.144 8 4.704 6 4.541 8] (″)降低至[0.106 8 0.107 2 0.133 3] (°)/h和[0.437 30.442 2 0.511 2] (″)，表明經過算法處理，二者估計誤差的離散程度有了明顯降低，同時經過算法處理，星敏感器輸出姿態精度由[14.423 0 13.197 4 12.743 5] (″)(3σ)提升至 [1.472 4

1.483 9 1.771 5] (″)(3σ)，即量級由10″提升至1″，在以上處理結果的基礎上，三軸事后處理精度由[6.412 5.851 5.634](″)(3σ)提升至[0.637 0.630 0.705] (″)(3σ)，其精度得到了大幅度的提升，證明了本文所提出的基于雙向濾波的兩步法校正是有效的。同時，對比表4與表2，可以看出，傅里葉參數估計精度有一定提升，尤其對于幅值較大的低階低頻分量估計精準度有較大提升，這也是星敏感器校正精度提高的重要原因，同時參數收斂周期也由7軌以上減少至2～4軌，證明了本文基于MLE的雙向自適應濾波算法的有效性。

圖9 第1次循環校正結果 Fig.9 Calibration results after the 1st circle

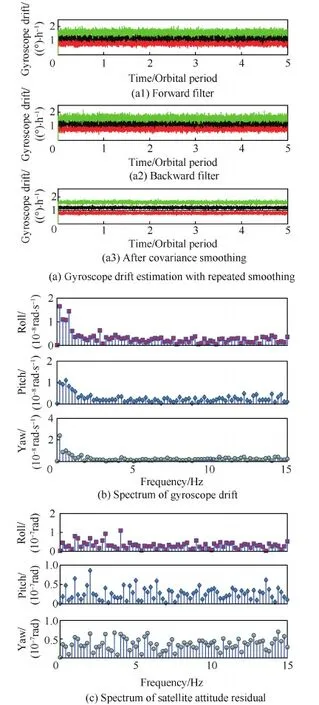
圖10 第3次循環校正結果 Fig.10 Calibration results after the 3rd circle

表3 基于反復濾波的兩步法校正結果Table 3 Calibration results of two-step repeated filtering algorithm

ParameterRoll(1st/2nd/3rdcircle)Pitch(1st/2nd/3rdcircle)Yaw(1st/2nd/3rdcircle)RMSofgyroscopedrift/((°)·h-1)0．8096/0．8076/0．80751．0072/1．0064/1．00601．1998/1．1990/1．1990RMSEofgyroscopedrift/((°)·h-1)0．0514/0．0482/0．04680．0515/0．0482/0．04730．0630/0．0602/0．0598Standardderivationofgyroscopedrift/((°)·h-1)0．1147/0．1075/0．10680．1163/0．1089/0．10720．1418/0．1355/0．1333Precisionofcalibratedstarsensor/(″)(3σ)14．4230/1．4922/1．472413．1974/1．5101/1．483912．743/1．8715/1．7715Standardderivationstarsensorerror/(″)5．1448/0．5173/0．43734．7046/0．5222/0．44224．5418/0．6512/0．5112Precisionofofflineattitudedetermination/(″)(3σ)6．412/0．638/0．6375．851/0．633/0．6305．634/0．785/0．705

表4 基于反復濾波的兩步法低頻誤差參數估計結果Table 4 LFE parameter estimation results of two-step repeated filtering algorithm

5 結 論

1) 針對低頻誤差與陀螺漂移的耦合影響進行數學分析，得到結論：無論將低頻誤差與陀螺漂移一同估計或分開估計，誤差估計過程中都會產生相互影響，但針對二者誤差特性不同，分開估計能夠獲得更優的估計效果。

2) 在上述結論的基礎上，提出一種基于雙向濾波的兩步離線校正算法，通過反復平滑獲得精準陀螺漂移估計，通過基于MLE的雙向自適應濾波算法獲得收斂精度較高的低頻參數估計，仿真表明，所提出的算法能有效剝離星敏感器低頻誤差與陀螺漂移間的耦合影響，提高離線姿態確定精度。

[1] IWATA T. Advanced land observing satellite (ALOS): On-orbit status and platform calibration[C]//Geoscience and Remote Sensing Symposium. Piscataway, NJ: IEEE Press, 2007.

[2] IWATA T, ISHIDA H, OSAWA Y. Advanced land observing satellite (ALOS): Enabling technologies and platform performance[C]//Proceedings of SPIE 71060, Sensors, Systems, and Next-generation Satellites XII. Bellingham, WA: SPIE, 2008.

[3] IWATA T， UO M, KAWAHARA T. Ground-based precision attitude determination using repeated smoothing with sequential rate bias and attitude estimation[C]//AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2010: 8451.

[4] IWATA T. Precision attitude and position determination for the advanced land observing satellite (ALOS)[C]//Proceedings of SPIE—The International Society for Optical Engineering. Bellingham, WA: SPIE, 2005: 5659.

[5] IWATA T, HOSHINO H, YOSHIZAWA T, et al. Precision attitude determination for the advanced land observing satellite (ALOS): Design, verification, and on-orbit calibration[C]//AIAA Guidance, Navigation and Control Conference and Exhibit. Reston: AIAA, 2007.

[6] LEI X, YANG J. Application of RTS optimal smoothing algorithm in satellite attitude determination[C]//International Conference on Intelligent Control and Information Processing. Piscataway, NJ: IEEE Press, 2011: 978-982.

[7] YANG J, LEI X. Satellite attitude determination in post-processing based on URTS optimal smoother[C]//2012 12th International Conference on Control, Automation and Systems (ICCAS). Piscataway, NJ: IEEE Press, 2012: 267-272.

[8] SARKKA S. Unscented Rauch-Tung-Striebel smoother[J]. IEEE Transactions on Automatic Control, 2008, 53(3): 845-849.

[9] 盧欣, 武延鵬, 鐘紅軍, 等. 星敏感器低頻誤差分析[J]. 空間控制技術與應用, 2014, 40(2): 1-7.

LU X, WU Y P, ZHONG H J, et al. Low frequency error analysis of star sensor[J]. Aerospace Control and Application, 2014, 40(2): 1-7 (in Chinese).

[10] 熊凱, 宗紅, 湯亮. 星敏感器低頻誤差在軌校準方法研究[J]. 空間控制技術與應用, 2014, 40(3): 8-13.

XIONG K, ZONG H, TANG L. On star sensor low frequency error in-orbit calibration method[J]. Aerospace Control and Application, 2014, 40(3): 8-13 (in Chinese).

[11] XIONG K, ZONG H. Performance evaluation of star sensor low frequency error calibration[J]. Acta Astronautica, 2014, 98: 24-36.

[12] 熊凱, 湯亮, 劉一武. 基于地標信息的星敏感器低頻誤差標定方法[J]. 空間控制技術與應用, 2012, 38(3): 11-15.

XIONG K, TANG L, LIU Y W. Calibration of star sensor’s low frequency error based on landmark information[J]. Aerospace Control and Application, 2012, 38(3): 11-15 (in Chinese).

[13] SCHMIDT U, ELSTNER C, MICHEL K. ASTRO 15 star tracker flight experience and further improvements towards the ASTRO APS star tracker[C]//AIAA Guidance, Navigation and Control Conference and Exhibit. Reston: AIAA, 2008.

[14] LAI Y W, LIU J H, DING Y H, et al. Precession-nutation correction for star tracker attitude measurement of STECE satellite[J]. Chinese Journal of Aeronautics, 2014, 27(1): 117-123.

[15] LAI Y W, LIU J H, DING Y H, et al. In-flight quality evaluation of attitude measurements from STECE APS -01 star tracker[J]. Acta Astronautica, 2014, 102: 207-216.

[16] 賴育網, 谷德峰, 劉俊宏, 等. 星敏感器/陀螺在軌系統誤差分析與校準[C]//第三屆高分辨率對地觀測學術年會分會論文集. 北京: 中國學術期刊電子出版社, 2014.

LAI Y W, GU D F, LIU J H, et al. In-flight systematic error analysis and calibration for star tracker/gyro[C]//3th China High Resolution Earth Observation Conference. Beijing: China Academic Journal Electronic Publishing House, 2014 (in Chinese).

[17] 王曉東. 大視場高精度星敏感器技術研究[D]. 長春: 中國科學院研究生院， 長春光學精密機械與物理研究所, 2003: 15-50.

WANG X D. Study on wild-field-of-view and high-accuracy star sensor technologies[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Graduate University of Chinese Academy of Science, 2003: 15-50 (in Chinese).

[18] ROGERS G D, SCHWINGER M R, KAIDY J T, et al. Autonomous star tracker performance[J]. Acta Astronautica, 2009, 65(1-2): 61-74.

[19] WANG J Q, XIONG K, ZHOU H Y. Low-frequency periodic error identification and compensation for star tracker attitude measurement[J]. Chinese Journal of Aeronautics, 2012, 25(4): 615-621.

[20] MOHAMED A H. Optimizing the estimation procedure in INS/GPS integration for kinematic applications[D]. Calgary: University of Calgary, 1999: 62-65.

(責任編輯： 張玉， 徐曉)

URL：www.cnki.net/kcms/detail/11.1929.V.20160801.1037.006.html

Offlinecalibrationmethodoflowfrequencyerrorofstarsensorandgyroscopedrift

ZHAOLin,XIERuida*,LIUYuan,HAOYong

SchoolofAutomation,HarbinEngineeringUniversity,Harbin150001,China

High-accuracypostattitudedataiscriticaltotheimprovementofimagequalityofremotesensingplatforms.Duringofflineprocessing,errorsofattitudesensorscanbeefficientlycalibratedtoachievehigherprecisionofattitudedetermination.However,couplinginfluenceoflowfrequencyerror(LFE)andgyroscopedriftcancausethedecreaseofcalibrationprecision.Inordertosolvetheproblem,amathematicalmodeloftheinfluenceisderivedinthispaper.Meanwhile,atwo-stepbidirectionalsmoothingalgorithmisproposedtocalibratedseparatelygyroscopedriftandLFE.GyroscopedriftandLFEcanbeperfectlyseparatedwiththeproposedmethod.InordertosolvetheproblemsofslowconvergenceofLFEparametersandthedifficultyoftuningnoiseparametersamaximum-likelihood-estimation(MLE)basedbidirectionaladaptivefilteringalgorithmisdeveloped,whichcanimprovebothconvergencespeedandprecisiondramatically.Underthesimulationconditioninthispaper,theaccuracyofofflineattitudedeterminationreaches0.8″(3σ)andtheconvergencetimeofLFEparametersisnotmorethan4orbitalperiods.

starsensor;lowfrequencynoise;gyroscopedrift;satelliteattitudemeasurement;post-processing;errorcalibrationofattitudesensor

2016-06-22；Revised2016-07-11；Accepted2016-07-18；Publishedonline2016-08-011037

s：NationalNaturalScienceFoundationofChina(61273081);HeilongjiangPostdoctoralScientificResearchDevelopmentFund(LBH-Q14054);theFundamentalResearchFundsfortheCentralUniversities(HEUCFD1503)

.E-mailxieruida_paper@163.com

2016-06-22；退修日期2016-07-11；錄用日期2016-07-18； < class="emphasis_bold">網絡出版時間

時間：2016-08-011037

www.cnki.net/kcms/detail/11.1929.V.20160801.1037.006.html

國家自然科學基金 (61273081)； 黑龍江省博士后科研啟動金 (LBH-Q14054)； 中央高校基本科研業務費專項資金 (HEUCFD1503)

.E-mailxieruida_paper@163.com

趙琳， 謝睿達， 劉源， 等． 星敏感器低頻誤差與陀螺漂移離線校正方法J． 航空學報,2017,38(5):320552.ZHAOL,XIERD,LIUY,etal.OfflinecalibrationmethodoflowfrequencyerrorofstarsensorandgyroscopedriftJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):320552.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0218

V448.2

A

1000-6893(2017)05-320552-14