自行車穩定性問題的研究與詮釋
黃紹書
(六盤水市第23中學 貴州 六盤水 553000)
蔣金團
(施甸縣第一中學 云南 保山 678200)
自行車穩定性問題的研究與詮釋
黃紹書
(六盤水市第23中學 貴州 六盤水 553000)
蔣金團
(施甸縣第一中學 云南 保山 678200)
根據剛體轉動的力矩平衡,從轉動相對定點懸空的角度,給出自行車“轉彎不倒”的約束關系,并由此剖析自行車在微小擾動情況下,能夠自動恢復穩定的原因.最后,結合自行車轉彎過程中的轉動慣量及回轉半徑,給出自行車在“轉彎不倒”條件下的最大角速度解析式.
自行車穩定性 轉彎不倒 陀螺效應 力矩平衡 詮釋
1 引言
自行車是最普及的大眾簡易交通工具,它的發明已有200多年.而對自行車穩定性問題的研究和討論,同樣具有悠久的歷史.這方面已發表的科普文章近百篇,通過檢索查閱近40年來的部分文獻資料[1~4],發現它們基本都是從動力學微分方程入手分析,而未離開流行上百年的離心力效應和陀螺效應的觀點.
關于自行車穩定性問題的研究和討論,從未停止,并曾幾度掀起熱潮.1970年,英國一位化學家Jones對傳統的陀螺效應產生懷疑[5].于是,他設計一輛無陀螺效應的自行車,就是在普通自行車的前輪上并排安裝一個同樣大小但不接觸地面的輪子,這一輪子與正常車輪反向轉動時,即可消除陀螺效應.Jones的這一實踐表明,消除陀螺效應后的高速運動的自行車同樣能夠維持穩定.也就是說,陀螺效應對自行車的穩定性沒有明顯的影響.
2012年1月,美國科普雜志Discover Magazine評選了2011年全球100個頂尖科學故事.其中“自行車的新物理”榮居第26位.為此,其困擾公眾的自行車穩定性問題再度熱議起來[6].
至如今,自行車穩定性問題仍然是一個懸而未決的科學懸案.本文試圖從轉動相對定點懸空的角度,分析給出自行車“轉彎不倒”的約束關系,并由此對自行車在微小擾動情況下,能夠自動恢復穩定的原因進行剖析.
2 從自行車“轉彎不倒”談起
騎著自行車轉彎時,人和車都總是向彎道的內側傾斜.因此,人和車組成的系統(以下簡稱人車系統)的重力作用線不在支撐面上,那么,為什么人車系統不會傾倒呢?
2.1自行車轉彎的一般認識
如圖1所示,騎著自行車在水平彎道轉彎時的情形.
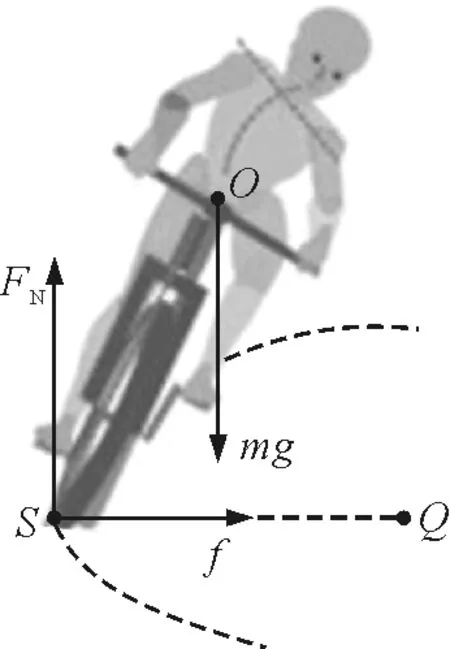
圖1 人騎自行車受力分析
為了減少計算的復雜性,這里將人車系統受到力簡化為3個,即人車系統的重力mg,路面對車輪的支持力FN及法向摩擦力f.設人車系統做圓周運動的角速度為ω,質心軌道半徑為r.那么,在豎直方向
FN-mg=0
(1)
即FN與mg等大反向,合力為零.
在水平方向
f=mrω2
(2)
即摩擦力f提供轉彎所需的向心力.
顯然,這一分析過程中,沒有考慮人車系統的空間尺度,也沒有考慮支持力FN與重力mg之間是非共點力的關系,僅將人車系統的轉動考慮成質點的圓周運動.因此,這一分析不能解釋“轉彎不倒”的問題.
2.2自行車“轉彎不倒”約束條件
事實上,人車系統是一個相對定軸轉動系統.那么,什么力的力矩與重力力矩平衡,使得人車系統“轉彎不倒”,而維系著動態平衡狀態呢?這就是公眾不能釋疑的根本性困擾.
為了便于討論,將人車系統簡化成剛體.人車系統轉彎時,實際是繞某一豎直軸轉動,其轉動面為一圓錐面,如圖2所示.受力情況與圖1一致,不再贅述.設人車系統的重心為O,轉動過程中的傾斜角為θ,轉動相對定點為P,轉動軸為過P點的豎直軸,路面支撐動點S與O,P之間的距離分別為l和L.那么,重力mg,支持力FN和摩擦力f對P點的力矩分別為
MG=mg(L-l)cosθ
(3)
MF=FNLcosθ
(4)
Mf=fLsinθ
(5)
由圖2可知,支持力FN與重力mg的大小是相等的.在人車系統逐漸傾斜過程中,主動力矩MG和MF將隨傾斜角θ的減小而增大,而被動力矩Mf的變化比較復雜,因為摩檫力f的大小與其力臂存在相反的變化趨勢.人車系統“倒”與“不倒”,完全決定于這3個力矩之間的約束關系,亦就是
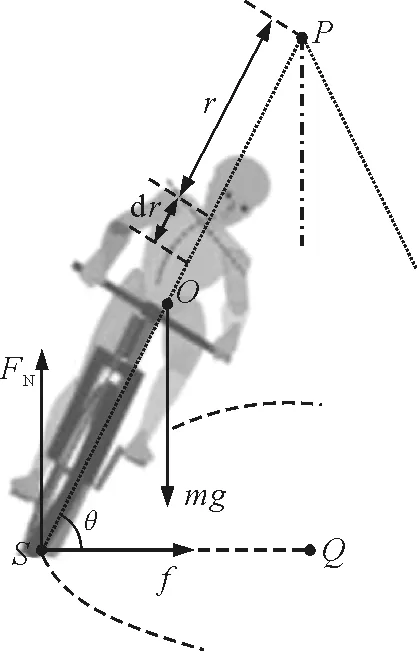
圖2 力矩之間的約束關系
(1)當Mf>MF-MG,即
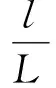
時,傾斜角θ將增大而“不倒”,且這與人為控制沒有多大的關系.
(2)當Mf=MF-MG,即
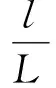
時,傾斜角θ將不變而“不倒”.
(3)當Mf 時,傾斜角θ將減小.若此時的摩擦力已達到最大靜摩擦力fm,則人車系統即刻“倒”;若此時的摩擦力未達到最大靜摩擦力fm,則人車系統隨著θ減小到一定值時仍然“倒”. 在人車系統轉彎的角速度沒有超過最大角速度之前,摩擦力的大小就處在零與最大靜摩擦力fm之間的變化,且摩擦力的大小由人車系統的轉動角速度、轉動半徑及傾斜角確定,見式(8)~(13)的推導.這時,摩擦力矩Mf也隨之變化. 自行車的穩定性是指正常沿直線自由高速行駛的自行車,在某種擾動情況下,其運動軌跡偏離直線后會自動(非人為控制)恢復直線穩定運動的現象. 自行車高速行駛條件下,在受到某種擾動時,由于前叉(龍頭)的靈活轉動,就會由直線運動變為圓弧運動.這時,車身向內傾斜,而車身“倒”與“不倒”符合圖2所示模型的上述討論. 高速行駛的自行車在受到微小擾動的情況下,轉動相對定點P的空間位置較高,車身的傾斜角θ較大,路面對車輪的法向摩擦力f的力臂較長,車身的重力mg和路面對車輪的支持力FN的力臂較短.根據圖2所示模型的討論可知,這時,這3個力對轉動相對定點P的力矩之間往往滿足 Mf>MF-MG 即 (6) 因此,這種情況下,車身的傾斜角θ會逐漸增大.這樣,就維持了自行車的穩定性.從式(2)可以看出,這時自行車的速度越大,其離心運動(向外側滑)的趨勢就越明顯,路面對車輪的法向摩擦力f就越大,自行車越容易自動恢復穩定運動狀態. 當自行車受到擾動比較劇烈時,轉動相對定點P的空間位置過度偏低,車身的傾斜角θ較小,路面對車輪的法向摩擦力f的力臂較短,車身的重力mg和路面對車輪的支持力FN的力臂較長.這時,這3個力對轉動相對定點P的力矩之間通常滿足 Mf 即 (7) 因此,這種情況下,車身的傾斜角θ會越來越小,自行車的穩定性將不能繼續維持. 這里還需特別說明,陀螺效應對于自行車的維持穩定確實有一定的作用.但是,由于自行車的車輪轉動角速度一般遠遠不及高速旋轉的陀螺角速度大,因此,陀螺效應對自行車的維持穩定的作用并不明顯.另外,自行車前叉(龍頭)的靈活轉動且呈傾斜狀的結構,對于自行車自動恢復穩定起著至關重要的作用. 人車系統轉彎的最大角速度ωm與人車系統對轉動定點(相對)P的轉動慣量J或回轉半徑r0[6]有關,同時還與人車系統的最小傾斜角θn有關. 再次將人車系統進一步看成質量均勻分布的細柱型剛體.根據前面設定,人車系統的豎直面總長度應為2l.令人車系統的線密度為λ.在距離圖2中的P點為r處,取一長度元dr,則長度元的質量為dm=λdr.因此,人車系統對轉動定點(相對)P的轉動慣量為 (8) 回轉半徑為 (9) 若設車輪與路面之間的最大靜摩擦因數為μm,那么,由圖2可知,人車系統轉彎的最小傾斜角θn滿足 (10) 由于地面對車輪的支持力FN等于人車系統的重力mg,因此人車系統轉彎過程中受到路面的最大靜摩擦力fm為 fm=μmmg (11) 這一最大靜摩擦力就是人車系統轉彎時的最大向心力.剛體繞定軸轉動時,由于轉動慣量的影響,向心力應等效作用于剛體的微分質量集中點.因此,人車系統轉彎過程中,最大角速度ωm滿足 fm=mr0ωm2cosθn (12) 代入各量代數式,化簡可得 (13) (1)人車系統在轉彎過程中,由于路面的平整度或人為因素,會使其受到隨機擾動,從而使圖2中的轉動相對定點P以及過該點的豎直軸具有瞬時性,具體可由人車系統的動力學微分方程瞬時關系確定.因此,各式中涉及的路面支撐點S與轉動定點P之間的距離L以及轉動慣量J,回轉半徑r0,最大角速度ωm等也都具有瞬時性. (2)根據(6)、(7)兩式的分析表明,本文的研究詮釋了自行車能夠自動恢復穩定的根本原因,解決了自行車穩定性這一懸而未決的問題. 1 馬中興.自行車的動力學方程及運動穩定性.陜西科學技術大學學報,1982(10):91~105 2 魏德明.論自行車的穩定性.昆明工學院學報,1986(2):117~122 3 徐華峰.自行車運動穩定性研究.振動與沖擊,1994(3):70~75 4 林修成,張朝陽.自行車行駛穩定性及后進動性的力學分析.合肥工業大學學報,2011(4):287~291 5 劉延柱. 關于自行車的穩定性. 力學與實踐, 2012(2): 90~93 6 哈爾濱工業大學理論力學教研室.理論力學(Ⅰ).北京.高等教育出版社.2009.259~272 ResearchandInterpretationonBicycleStabilityIssue Huang Shaoshu (Liu Panshui No.23 Middle School,Liu Panshui,GuiZhou 553000) Jiang Jintuan (ShiDian No.1 Middle School,BaoShan,YunNan 678200) According to the rigid body rotation moment balance,from the Angle of rotation relative fixed-point dangling give bicycle turn "fail" constraints,and analyze the bike under the condition of small disturbance,automatically restore stability.Finally,the maximum angular velocity resolution of the bicycle in the condition of "turn down" is given by the rotational inertia and the radius of rotation. bicycle stability;turning to fail;centrifugal effect;the gyroscopic effect;conical surface;torque balance;interpretation 2017-05-25)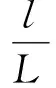
3 自行車穩定性的剖析
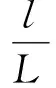
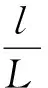
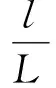
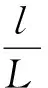
4 最大角速度



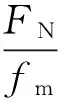

5 說明與結論

