淺談牛頓定律與參考系

胡 敏 郭長江 顧 鋒

(上海師范大學數理學院 上海 200234)

淺談牛頓定律與參考系

胡 敏 郭長江 顧 鋒

(上海師范大學數理學院 上海 200234)

對牛頓定律與參考系之間的關系作簡要的梳理．首先，由牛頓第一定律著手，分析慣性參考系與非慣性參考系的本質區別．再基于對牛頓第二定律的理解，從“F=m(a相+a參)”與“F-ma參=ma相”兩式的區別與聯系出發分析慣性參考系與平動非慣性參考系的關系，并對轉動非慣性參考系中各慣性力的物理意義作展開解釋．最后，指出牛頓第三定律與參考系的選取無關．

牛頓定律 慣性參考系 非慣性參考系 慣性力

在中學物理教學中，通常選取地球當做參考系，忽視了參考系在經典力學中的重要作用．在討論牛頓運動定律時，學生往往會出現很多混淆不清的問題．

針對此現狀，本文對牛頓定律與參考系之間的關系作簡要梳理，并從牛頓第二定律的定量表達式出發對非慣性系中的各慣性力作展開解釋．

1 牛頓第一定律與參考系

在力學中，根據牛頓定律是否成立將參考系分為了慣性參考系和非慣性參考系．在牛頓三大定律中，牛頓第一定律給出了力的本質與慣性定律，是其他兩條定律的前提和基礎，故若一個參考系中物體的運動狀態滿足牛頓第一定律，其必然也滿足第二與第三定律．據此，多數學者對其做出了相應的定義：在一定精度下，使牛頓第一定律成立的參考系叫慣性參考系；使牛頓第一定律不能成立的參考系叫非慣性參考系．因此從某種程度上說，牛頓第一定律定義了慣性系與非慣性系．

2 牛頓第二定律與參考系

牛頓第二定律是以牛頓第一定律為基礎，對力與物體的運動狀態變化的關系作的定量表述，其直接提供了物體所受合外力與其加速度之間的關系，通常表示為F=ma．我們知道，非慣性參考系與慣性參考系之間存在著相對的加速度，那么牛頓定律如何應用于非慣性系中？兩參考系之間又有何關系呢？下面，基于牛頓第二定律來理解慣性參考系與非慣性參考系之間的關系以及非慣性系中各慣性力的物理意義．

2.1從“F=m(a相+a參)”與“F-ma參=ma相”兩式出發理解慣性系與平動非慣性系

“F=ma”是牛頓第二定律最普遍的數學表達式．對于牛頓第二定律有以下解釋：“F”為作用在質點或質點系上的合外力，“m”為質點或質點系的質量，“a”為質點或質點系運動的加速度．考慮到參考系的運動，絕對加速度可表示為：a=a相+a參，即F=ma=m(a相+a參)，其中“a相”為質點或質點系相對于參考系的加速度，“a參”為參考系的加速度．則等式“F=m(a相+a參)”的左邊表示合外力，右邊表示質點或質點系運動狀態的變化．

現將等式“F=m(a相+a參)”變形為“F-ma參=ma相”，若還以上述“等式左邊表示合外力，等式右邊表示運動狀態”的思想出發，可以發現其物理意義發生了巨大的變化．此時，等式左邊“F-ma參”表示質點或質點系所受的合外力，而等式右邊則表示其加速度為a相．

那么，這兩個公式分別可適應用于哪些具體情境中呢？

現有兩個參考系，地面參考系與動參考系，將地面參考系默認為慣性參考系，若動參考系相對于地面做直線加速運動，則為平動非慣性參考系．在慣性參考系中，牛頓第二定律適用，但在非慣性參考系中，牛頓第二定律就出現了問題．可以考慮一個簡單情景：如圖1所示，有一輛小車在地面上做勻加速直線運動，有一個質量為m的質點在小車內受到恒力作用做勻加速直線運動．

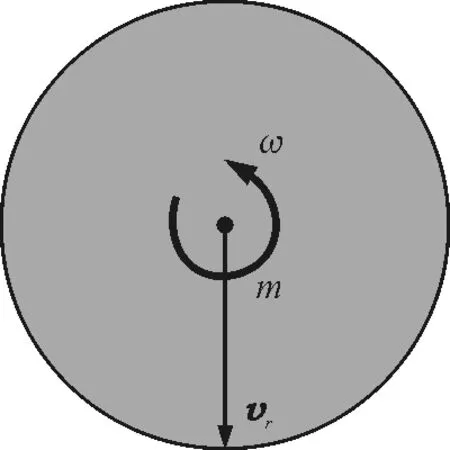
圖1 質點運動示意圖

定義水平向右為正方向，并令小車加速度為a參，則質點相對于小車的加速度為a相．以地面為參考系時，根據牛頓第二定律可列出方程：F=ma=m(a相+a參)．而以小車為參考物時，出現了矛盾：在小車中觀察，質點的加速度為a相，根據牛頓第二定律得到方程：F=ma相，與上述方程“F=m(a相+a參)”產生矛盾，而導致這一矛盾的特殊所在是平動非慣性系相對慣性系具有加速度a參．為了解決這一矛盾，使牛頓第二定律在平動非慣性參考系中仍然適用，我們可以認為在非慣性系中的一切物體都受到某種大小為“-ma參”的力的作用，借以平衡此參考系相對于慣性參考系的加速度，此力稱為慣性力F*，即F*=-ma參，其中“m”為非慣性系中被研究的質點或質點系的質量，“a參”為非慣性參考系相對慣性參考系的加速度，負號表示其方向與相對加速度方向相反．于是，在上述平動非慣性參考系中，質點的合外力為“F-ma參”，且其加速度為a相，從而滿足等式“F-ma參=ma相”．

從“等式左邊表示合外力，等式右邊表示運動狀態”的思想分析上述情景，可用等式“F=m(a相+a參)”來描述慣性系中質點的運動，引入慣性力后，用等式“F-ma參=ma相”來描述平動非慣性系中質點的運動．可見在具體情景下兩式的物理含義大相徑庭，但其歸根結底都是牛頓第二定律的數學表達式．其實，轉動非慣性系在引入一些慣性力后也可應用牛頓第二定律，下文將具體介紹．這樣一來，在慣性參考系與非慣性參考系中皆可應用牛頓定律．所以說，慣性參考系與非慣性參考系是等價的．

2.2基于牛頓第二定律理解轉動非慣性系中慣性離心力與科里奧利力的物理意義

根據參考系相對于慣性參考系的加速度的不同，非慣性參考系可以分為平動非慣性參考系和轉動非慣性參考系兩大類．上述情景就是簡單的平動非慣性系，但由于地球本身的自轉，其實際是一個轉動非慣性系，所以地球上的物體更多需要利用轉動系來解決問題．

在轉動非慣性參考系中的物體也存在著慣性力，包括慣性離心力與科里奧利力．我們知道，平動非慣性系中慣性力的作用是平衡物體受到的恒力，那么同樣是慣性力，在轉動非慣性系中為什么又要引入慣性離心力與科里奧利力這兩個力呢？它們分別具有什么物理意義呢？

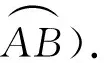
圖2 轉動非慣性系中質點的運動

圖3 慣性系中觀察質點的運動軌跡

首先，在慣性系中建立x-y-z三維坐標，使x-y坐標系的原點為轉盤圓心，則徑向單位矢量的方向會隨著圓盤轉動的角度θ改變，得

er(t)=cosθ(t)ex+sinθ(t)ey

對時間求導，可得

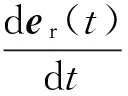
ωez×er(t)=ω×er(t)

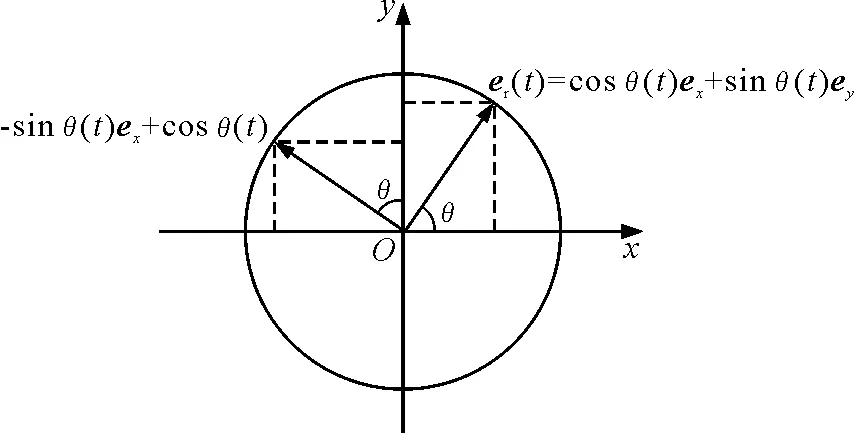
圖4 x-y平面解析圖

由r=r(t)er(t)，對時間求導可得

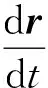
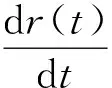
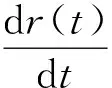
下面，先對徑向速度vr求導，可得徑向加速度為

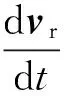
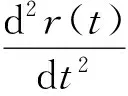
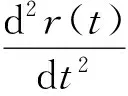
再對切向速度vt求導，可得切向加速度為

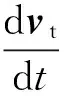
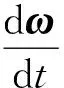
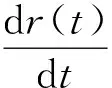
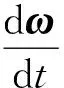
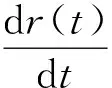
因此，總加速度為

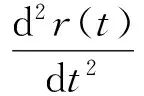
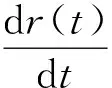
ω×[ω×r(t)er(t)]

由此可以發現，質點相對于慣性系的加速度共由五部分組成，則其實際所受到的合力也一定可分為這五部分，根據牛頓第二定律求得質點受到的合外力為

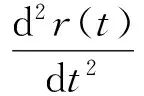
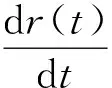
mω×[ω×r(t)er(t)]

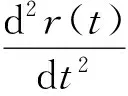
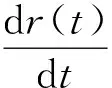
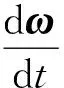
mω×[ω×r(t)er(t)]

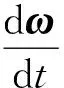
3 牛頓第三定律與參考系

通過引入慣性力，牛頓第一定律和第二定律能夠從慣性參考系推廣到非慣性參考系，那么牛頓第三定律也是如此嗎？

我們知道，牛頓第三定律揭示了作用力與反作用力之間的關系．當我們談及作用力時，總是有施力物體與受力物體，但慣性力是我們在出現矛盾時假想出來的力，并非真實存在的，因此它并沒有真正的施力物體．而物體之間的作用又是相互的，沒有施力物體也即沒有受力物體，所以慣性力不存在反作用力，它不屬于相互作用力的范疇．因此，我們在討論牛頓第三定律的適用性時不需要考慮慣性力．

在驗證牛頓第三定律的實驗中，通常選用兩個力傳感器進行互拉，我們會發現無論這兩個力傳感器是靜止的、勻速運動的還是變速運動的，它們在計算機上顯示的示數總是相等．若以地面為慣性參考系，那么靜止和勻速運動時的力傳感器都屬于慣性系；而當力傳感器變速運動時，它們自身就屬于非慣性參考系．此時相等的示數說明：在不附加其他條件的情況下，牛頓第三定律在非慣性系中仍然適用．因此，牛頓第三定律在慣性系與非慣性系中都適用．也即是說，牛頓第三定律與參考系的選取并沒有必然的聯系．

4 總結

從定性的角度而言，牛頓第一定律定義了慣性系與非慣性系；從定量的角度來說，從牛頓第二定律的定量表達式出發引入了慣性力，以此平衡在非慣性系中物體受到的真實力，使牛頓第一與第二定律在非慣性系中仍然適用；對于牛頓第三定律，描述的是相互作用力之間的關系，不需要考慮不屬于相互作用的慣性力，因此牛頓第三定律與參考系的選取無關．

1 馮杰.大學物理專題研究.北京:北京大學出版社,2011.95～108

2 漆安慎,杜嬋英.力學(第二版).北京:高等教育出版社,2005.85～91

3 周衍柏. 理論力學.北京:高等教育出版社,1997.180～186

TalkingabouttheNewton′sLawandtheReferenceSystem

Hu Min Guo Changjiang Gu Feng

(Mathematics & Science College of Shanghai Narmal University,Shanghai 200234)

This paper briefly sorts out the relationship between Newton′s law and the reference system. Firstly,Newton′s first law is used to analyze the essential difference between the inertial reference system and the non-inertial reference system. Then, based on the understanding of Newton′s second law, the relationship between the inertial reference system and the translational non-inertial reference system is analyzed from the distinction and contact between ′F=m(a相+a參)′and ′F-ma參=ma相′.And the physical meaning of the inertial forces in the rotatingnon-inertial reference system is explained. Finally, it is pointed out that Newton's third law has nothing to do with the selection of the reference system.

Newton′s law;inertial reference system;non-inertial reference system;inertial forces

作者介紹：胡敏(1994- )，女，在讀碩士研究生.

指導教師：郭長江(1974- )，男，中教高級，主要從事中學物理課程與教學研究.

2017-03-13)