對勻強磁場中球面擺運動規(guī)律的研究

姜付錦

(武漢市黃陂區(qū)第一中學 湖北 武漢 430300)

郎 軍

(重慶市第十一中學校 重慶 400061)

對勻強磁場中球面擺運動規(guī)律的研究

姜付錦

(武漢市黃陂區(qū)第一中學 湖北 武漢 430300)

郎 軍

(重慶市第十一中學校 重慶 400061)

通過對勻強磁場中一種球面擺運動的理論研究，證明了其正則角動量守恒，分析了當小球的速率有微擾時運動的定量規(guī)律以及不脫離而穩(wěn)定運動的條件，最后通過數(shù)值模擬直觀地顯示了運動軌跡并驗證了理論分析的結果．

球面擺 微擾 正則角動量 數(shù)值模擬

1 提出問題

如圖1所示，半徑為R的光滑球面固定在空間某點，磁感應強度為B的勻強磁場豎直向下穿過球面．一個質量為m，帶電荷量為+q的小球正在某一個水平面上做勻速圓周運動，已知小球與球心連線與豎直方向上的夾角為θ0，若小球的速度突然有一個變化量±Δv(方向不變)時，試分析以后小球的運動規(guī)律．

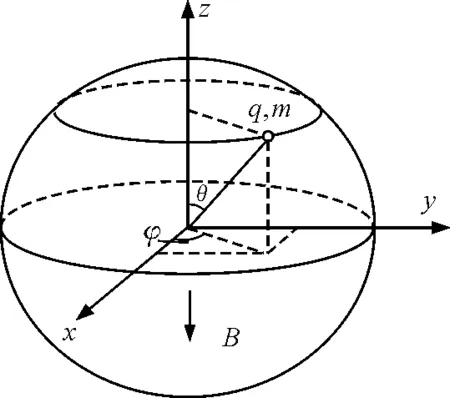
圖1 提出問題

2 理論研究

2.1理論依據(jù)

2.1.1 動力學方程

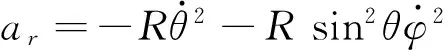
兩個方向上的分速度為

在er方向：

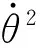
化簡得

FN=mgcosθ+qBvφsinθ-

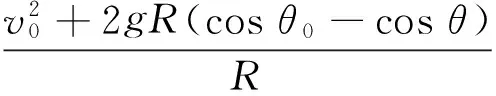
(1)

在eθ方向：

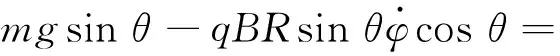
eφ方向：

由以上兩式求得

2.1.2 正則角動量守恒和機械能守恒

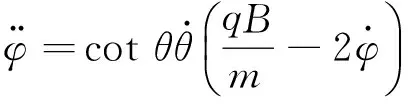
變?yōu)?/p>

等式兩邊同時乘于sinθ，并對時間不定積分得

即

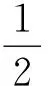
(2)

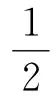
將小球的運動分解為經(jīng)線運動和緯線運動，由機械能守恒和正則角動量守恒有

經(jīng)線

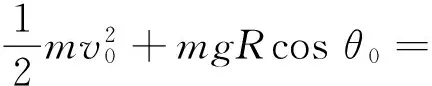
緯線

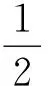
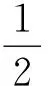
聯(lián)立以上兩式求得

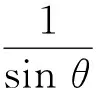
(3)

(4)

(5)

2.2運動規(guī)律

2.2.1 做穩(wěn)定圓周運動的初速度條件

設初速度為v0,要做穩(wěn)定圓周運動，則

由式(5)得

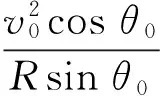
化簡得

求得

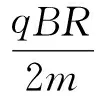
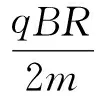
2.2.2 變軌運動規(guī)律

以下討論中，設+q被雙向約束在球面上(如設想有一根輕桿與+q相連，輕桿可繞球心各向自由轉動)，如圖2所示.

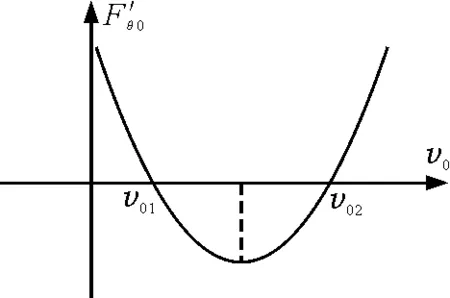
圖2 極角合力與初速度關系

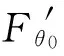
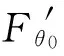
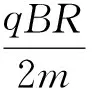
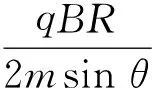
(6)

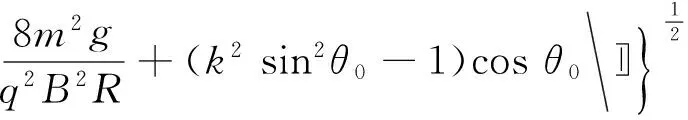
(7)

(8)

FN=3mgλ-2mgcosθ0+

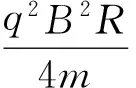
(9)

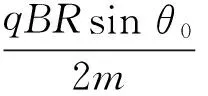
(2)最高點(或最低點)的極角θm

在最高點(或最低點)：vθ=0，由式(7)得

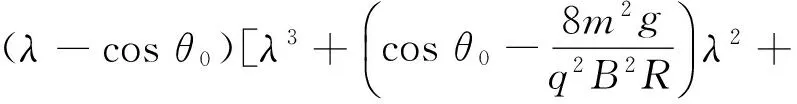
得

λ1=cosθ0

和

令

由一元三次方程的卡爾丹公式可得

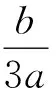
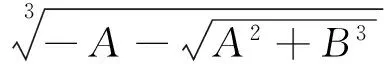
(10)

式中

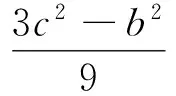
而λ3,λ4為復數(shù)根(舍去)，所以

θm=arccosλ2

討論：

(1)若k=0，式(7)變?yōu)?/p>

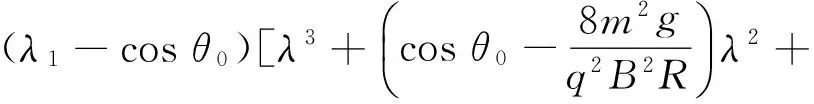
(k2sin2θ0-1)cosθ0]=0

進一步化簡為

(λ1-cosθ0)(λ-1)(λ+1)

這里λ1=cosθ0為初態(tài)值，λ2為最高點值，λ3,λ4舍去．

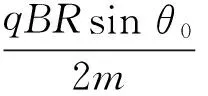
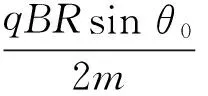
(3)沿經(jīng)線方向的運動周期Tθ

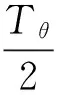
(11)

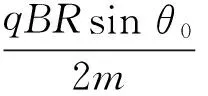
在一個周期內，沿緯線方向轉過的角度Δφ.

由于

所以

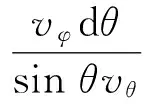
軌跡閉合性的條件：n1Δφ=n22π(n1,n2為正整數(shù))．

2.2.3 不脫離的條件

(1)如果|k|值太大，初始狀態(tài)可能就會脫離球面，由θ=θ0時，F(xiàn)N≥0求出k0.

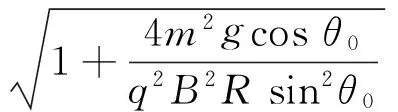
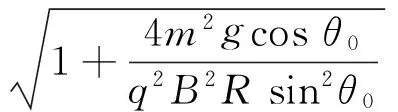
(12)

(2)如果|k|值太小，在向上變軌的過程中會出現(xiàn)脫軌，要求運動軌跡的最高點不脫離球面，由FN(θ)≥0,vθ(θ)=0可求得k1.

利用式(9)，由FN(θ)=0求得

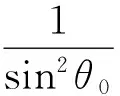
(13)

由vθ=0及式(7)和式(13)化簡得到一個關于λ的一元三次方程

λ3+bλ2+cλ+d=0

式中

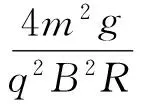
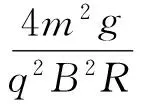
由卡爾丹公式[參見式(10)]可得求得λ.

由求得的λ代入式(13)可求得k絕對值，設為k1．

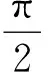
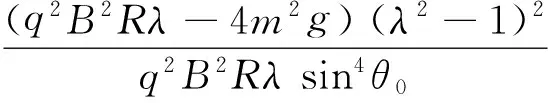
(14)

將k2的值代入vθ=0，利用式(7)，化簡有

因此λ1=λ2=cosθ0(這為初態(tài)值，不是我們要求的情況，舍去)

于是得到

由卡爾丹公式求得λ3的值(另兩解為復數(shù)解，舍去．)

將λ3的值代入式(14)求得k2的值．

(4)不脫離的條件為：k1≤|k|≤min(k0,k2)，若k1無解，則|k|≤min(k0,k2)

(5)實例分析

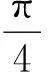
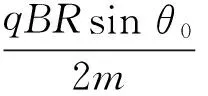
因此不脫離的條件為：0.784<|k|<1.068

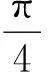
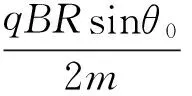
因此不脫離的條件為：|k|<0.713.

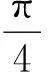
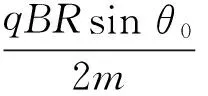
因此不脫離的條件為：0.905<|k|<1.031.

2.3特例分析

2.3.1 當v0=0時

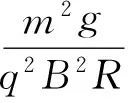
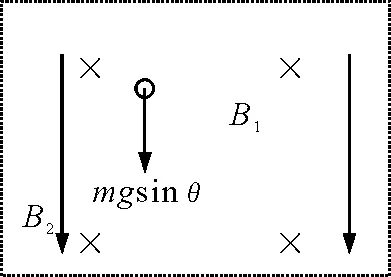
圖3 小球在近似平面上的運動

圖4

2.3.2v0=v01±Δv或v0=v02±Δv,Δv?v01或Δv?v02

(1)在這種微擾下，小球在經(jīng)線方向極角的變化非常小，在經(jīng)線方向近似做簡諧運動.

(2)振動周期的計算

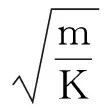
式中

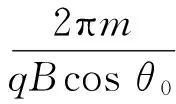
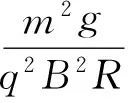
v02±Δv與v0=v01?Δv兩種情況的Tθ相同，結合特例1可知兩種情況下均有

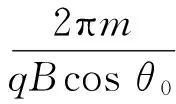
3 數(shù)值模擬

在Mathcad中輸入有關微分方程及初始條件，設置好q，m，g，B，v0等有關參數(shù)后，可以得到不同條件下小球運動規(guī)律的數(shù)值模擬結果．

3.1實例1的數(shù)值模擬

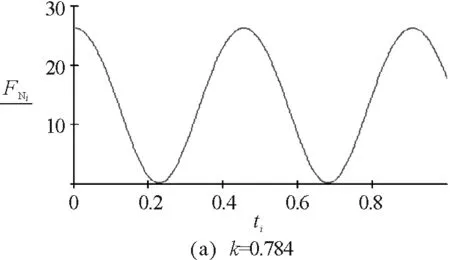
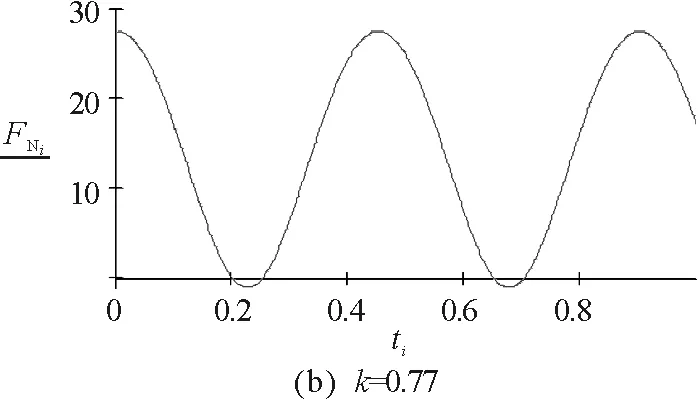
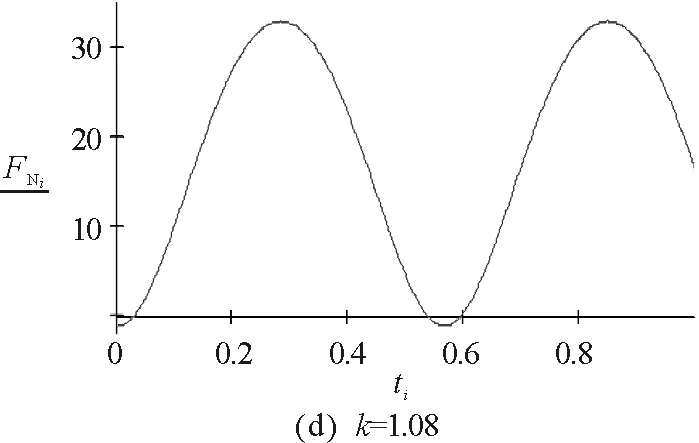
圖5 實例1的數(shù)值模擬

3.2實例2的數(shù)值模擬

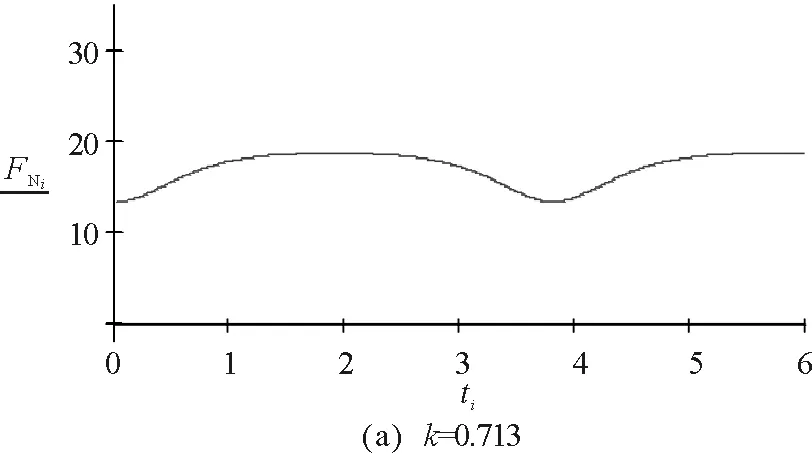
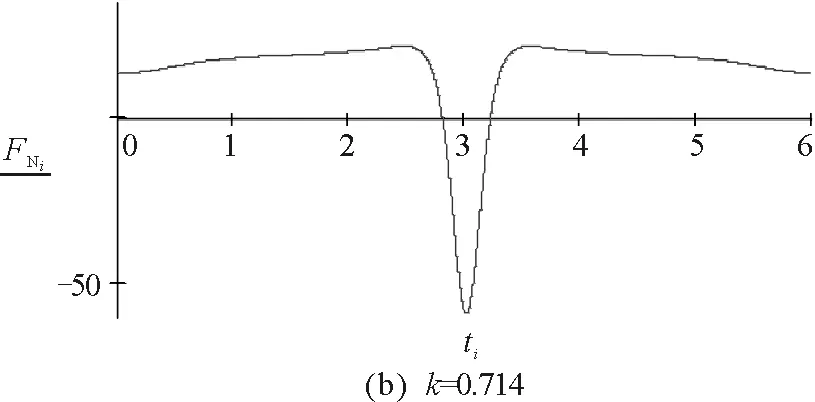
圖6 實例2的數(shù)值模擬

3.3實例3的數(shù)值模擬

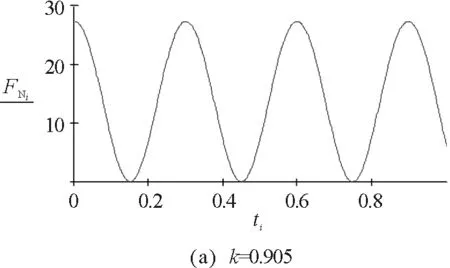
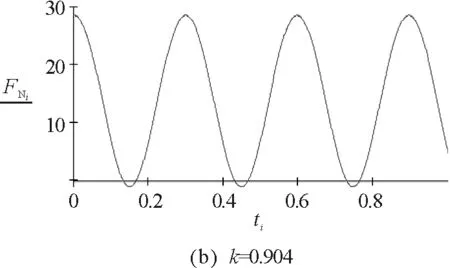
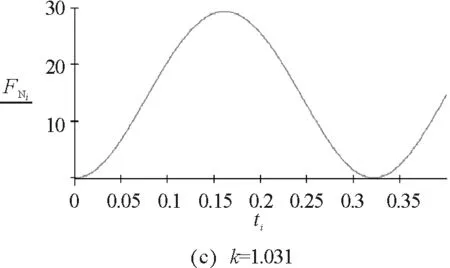
圖7 實例3的數(shù)值模擬

3.4小球運動軌跡的數(shù)值模擬

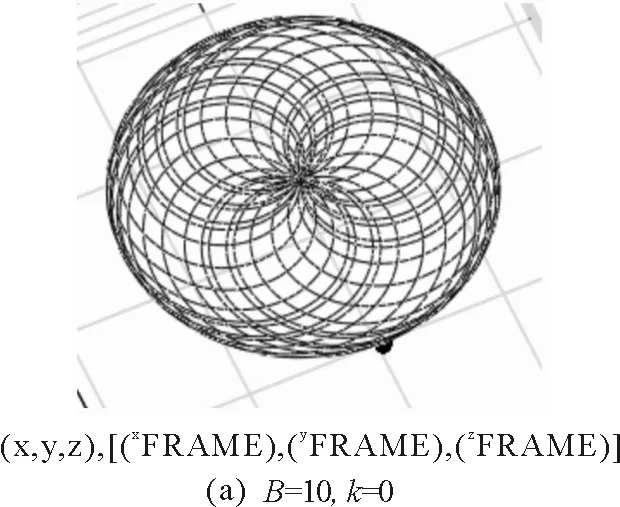
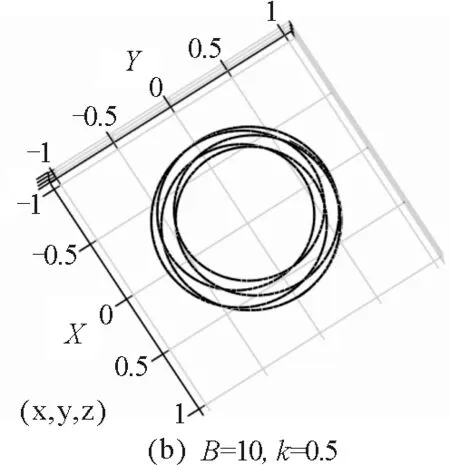
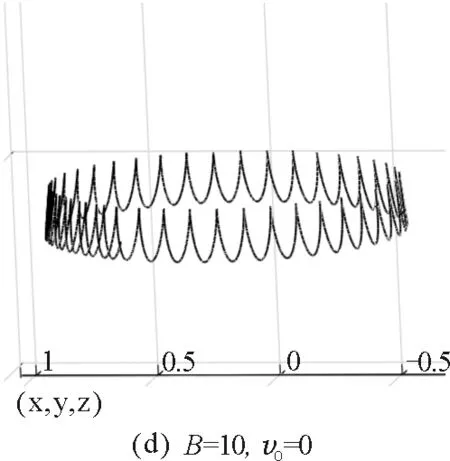
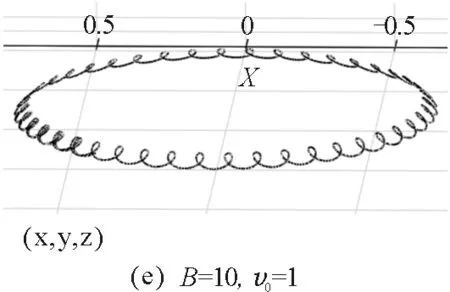
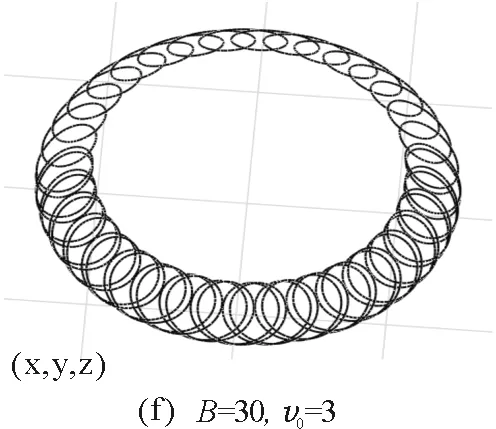
圖10 小球在不同初始值時運動軌跡的數(shù)值模擬

4 結束語

1 何廣源，黃迺本.球面擺的運動方程數(shù)值模擬和實驗驗證．大學物理，2006，25(7)：46～49

2 趙凱華.磁場中正則動量守恒定律的應用．大學物理，1988，1(3)：9

3 涂德新.復合場中的守恒量．物理通報，2016(4)：69～71

2017-04-24)