關于特征值及特征向量的教學分析
(鹽城工學院 數理學院,江蘇 鹽城 224003)
關于特征值及特征向量的教學分析
卞小霞
(鹽城工學院 數理學院,江蘇 鹽城 224003)
工程技術及科學研究中的很多問題常可歸結為求矩陣的特征值、特征向量的問題,結合教學實踐探討如何引起學生的學習興趣,如何講解概念、性質并進行延伸分析。
特征值;特征向量;矩陣;應用
特征值和特征向量是重要的代數概念,在經濟、工程、基礎研究等領域都有廣泛的應用。例如,特征值的符號可以確定一類工程系統的穩定性,可以判斷特定經濟模型的有效性等,而判斷依據特征值、特征向量的概念比較抽象,其概念及性質適合引導學生自主發現、探索,有利于培養學生的分析能力和創新能力。國內不少高等代數教材及線性代數教材[1-3]都以行列式為工具介紹特征值理論,文獻[4-5]介紹了特征值理論的非行列式觀點。本文在已有理論的基礎上,結合學校線性代數作為工科學生公共基礎課的教學實踐,分析了更為合理的特征值、特征向量的教學設計。
一、創設情境、激發興趣
通過現實生活中的例子說明教學內容的重要性,比如,橋梁坍塌的實例。塔科馬海峽大橋于1940年建成,位于美國華盛頓州,而同年11月7日,在19 m/s的低風速下因顫振而破壞,此消息震驚了世界,也引起了科學家們對振動問題的研究,正是他們的研究為后人減少了很多不必要的災害。
在振動問題的研究中,很多數學模型為常微分方程,常微分方程是在高等數學中已經學過的知識點,我們學習了各種求解方法,但仍有很多方程較難求解,此時,方程的穩定性可以不需要求出具體解,而只通過一階項系數矩陣的特征值來判斷。
比如某實際問題的數學模型為:
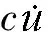
(1)
為了分析其平衡點的穩定性,首先將方程改寫成:
(2)
其派生系統為:
(3)
該系統有唯一的平衡點(0,0),對于派生系統(3),系數矩陣的特征值有一個為正值,則(0,0)是不穩定的鞍點,由Lyapunov穩定性定理[6]知原系統(1)在(0,0)處也是不穩定的,那么對于這個實際問題,需要修正它的結構參數才能使其穩定。
在上述問題分析過程中,避開了求解較復雜的常微分方程,只是利用系數矩陣的特征值進行了判斷。什么是特征值?如何求解矩陣的特征值呢?
二、概念剖析、性質初探
定義[2]:設A是n階矩陣,如果數λ和n維非零列向量x使關系式
Ax=λx
(4)
成立,那么,這樣的數λ稱為方陣A的特征值,非零向量x稱為A的對應于特征值λ的特征向量。
學生在高等數學中利用λ作為拉格朗日乘數求極值問題。此處,若是求滿足約束xTx=k時xTAx的極值,則構造拉格朗日函數L=xTAx-λ(xTx-k),令▽L=2Ax-2λx=0,得到Ax=λx時,可取得xTAx的極值。可見極值問題中,λ正是特征值的定義,這是從表達式的角度直接詮釋了特征值的意義。

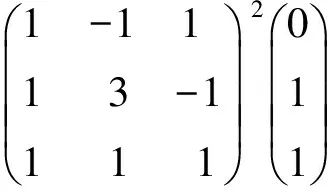
由例1的結果,學生會提出問題:

2.對于一般的n階方陣A,x≠0,λ∈R,若Ax=λx,則Anx=λnx嗎?
3.定義中的λ,x怎么求?
這三個問題的討論也是對特征值性質的分析。
三、問題追蹤、歸納方法
對于問題1,結合例1中已做的計算,再由n=k的假設,可得n=k+1的結論,根據數學歸納法,得到問題1的回答是肯定的;對于問題2,k=1時,Ax=λx,設k=n時,Anx=λnx,則k=n+1時,
An+1x=A(Anx)=A(λnx)=
λn(Ax)=λnλx=λn+1x
故問題2的回答也是肯定的。
對于問題3,要使Ax=λx有非零解x,即(A-λI)x=0有非零解,由齊次方程組有非零解的充要條件是|A-λI|=0,解得特征值λ,代入(A-λI)x=0,得到解x為對應的特征向量。
由以上分析歸納得到求解方陣的特征值、特征向量的一般方法:
(1)稱|A-λI|=0為特征方程,此方程為一元高次方程,求解得到所有的特征根λ1,λ2…λn;
(2)對每一個λi求出方程(A-λiI)x=0的基礎解系,相應的通解即為對應于λi的全部特征向量。
四、例題講解、性質總結
例2:求出下列方陣的全部特征值和特征向量。
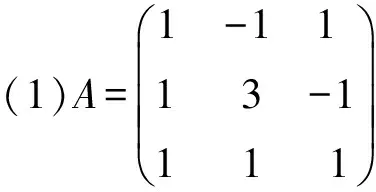
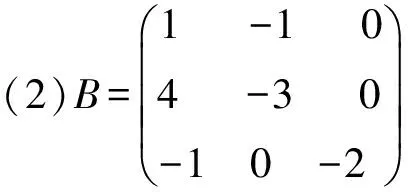
這兩個小例題介紹的特征值與特征向量對應情況由淺入深,(1)(2)的特征值都有重根,(2)中重根對應的線性無關的特征向量個數小于重根數,為引入性質奠定基礎,考慮其實際意義,矩陣(1)對應的系統在平衡點(0,0,0)處不穩定;矩陣(2)對應的系統在平衡點(0,0,0)處漸進穩定。
講解完例2,介紹以下性質:
性質1:若λ是方陣A的特征值,則λk是方陣Ak的一個特征值,k∈N;
性質2:方陣A的屬于不同特征值的特征向量是線性無關的;
性質3:任一特征值的代數重數不小于它的幾何重數。
性質1由前面例1總結可得,性質2由線性無關的定義容易證得,而性質3可由學生課后討論總結。
五、擴展應用、延伸分析
由矩陣的特征值,可以容易得到矩陣行列式的值、跡、慣性、是否可逆、能否對角化等,此外,也可得到矩陣多項式的特征值、逆等,這些延伸性的應用大多是在實際工程技術、科學研究中的收獲。為了讓學生體會到這一點,有必要作如下學習要求:
1.了解特征值、特征向量在工程技術領域的應用情況,學生通過查閱相關資料,總結出應用報告;
2.本節課介紹了利用行列式的方法求得特征值,請學生嘗試用其他的方法求得特征值[3-4];
3.課堂上沒有嚴格證明的性質,請學生補充證明過程。
六、結論
本節課設計由生動的引例引出了特征值、特征向量的概念,認識了特征值和特征向量能解決的問題,通過方程分析找到了求特征值、特征向量的一般方法,歸納了特征值與特征向量的性質。
特征值及特征向量的概念本身具有實際的背景意義,相關內容豐富,應用廣泛,研究的方法多樣,與學生一起探討分析有利于他們研究能力、創新能力的培養。
[1]北京大學數學系幾何與代數教研室代數小組.高等代數(第二版)[M].北京:高等教育出版社,2003.
[2]同濟大學數學系.工程數學線性代數[M].北京:高等教育出版社,1990.
[3]陳萬勇,等.線性代數[M].北京:電子工業出版社,2013.
[4]鄧勇.關于矩陣特征值理論的教學新設計[J].數學教育學報,2015,24(6):44—46.
[5]鐘鳳遠,王樹忠,葛斌.矩陣初等變換的應用[J].哈爾濱師范大學自然科學學報,2016,32(1):19—21.
[6]胡海巖.應用非線性動力學[M].北京:航空工業出版社,2001.
AnalysisonEigenvaluesandandEigenvectorofMatrixTeaching
BIAN Xiao-xia
(School of Mathematics and Physics, Yancheng Institute of Technology, Yancheng 224003, China)
Many problems in science and technology research projects often can be attributed to the eigenvalues and eigenvector of matrix. The paper explores how to arouse students’ interest in learning, how to explain the concept, nature and make an extension analysis combined with the teaching practice .
eigenvalue; eigenvector; matrix; application
10.3969/j.issn.1008-6714.2017.11.028
O172.1
A
1008-6714(2017)11-0068-03
2017-07-12
卞小霞(1984— ),女,江蘇鹽城人,講師,博士研究生,從事一般拓撲學研究。
〔責任編輯:李海波〕

