腔體雙邊二次電子倍增一階與三階模式瞬態特性對比?

董燁 劉慶想龐健 周海京董志偉

1)(西南交通大學物理科學與技術學院,成都 610031)

2)(北京應用物理與計算數學研究所,北京 100094)

3)(中國工程物理研究院流體物理研究所,綿陽 621900)

腔體雙邊二次電子倍增一階與三階模式瞬態特性對比?

董燁1)2)?劉慶想1)龐健3)?周海京2)董志偉2)

1)(西南交通大學物理科學與技術學院,成都 610031)

2)(北京應用物理與計算數學研究所,北京 100094)

3)(中國工程物理研究院流體物理研究所,綿陽 621900)

雙邊二次電子倍增,瞬態演化,蒙特卡羅方法,粒子模擬方法

為評估高階模式二次電子倍增對加速器射頻腔動態建場過程的影響,采用蒙特卡羅與粒子模擬相結合的方法對金屬無氧銅腔體雙邊二次電子倍增一階與三階模式的瞬態演化及飽和特性進行了數值模擬對比研究.研究結果表明:二次電子倍增過程中,二次電子數目、放電電流、放電功率、沉積功率隨時間呈現以指數形式快速增長后趨于飽和振蕩的物理規律;相對一階模式,三階模式的飽和值更低且上升時間更長.放電電流存在延時現象,由此引發了二次電子倍增過程中部分充電現象的出現.統計發現平均放電功率等于平均沉積功率,三階模式的放電功率大約是一階模式1%的水平,由此判斷加速器腔體動態建場過程中高階模式的影響較小.二次電子倍增過程中,一階模式呈現單電子束團加速運動特性,而三階模式則呈現加速/減速/加速及多電子束團相向運動的復雜特性;二次電子倍增進入飽和后,三階模式的空間電荷效應明顯弱于一階模式.

1 引 言

二次電子倍增是由二次電子驅動的一種真空共振放電現象,其可以在很多結構下產生,如加速器、微波器件的腔體結構表面、微波輸出窗表面以及人造衛星敏感器件內部,并導致嚴重后果,包括射頻擊穿、建場失敗、沿面閃絡以及噪聲干擾等.作為一種最為基本的二次電子倍增類型,金屬雙邊二次電子倍增已經被人們所廣泛研究過.Vaughan[1]建立了細致的動力學理論分析模型并得到了聚焦相位條件,Kishek等[2]給出了共振方程并據此給出了雙邊二次電子倍增的敏感曲線,Kishek和Lau[3]利用電子面片簡化模型研究了雙邊二次電子倍增與外電路互作用的過程,最近還發現并證明了ping-pong類型雙邊二次電子倍增的存在[4].

國內外許多工作都是采用基于粒子軌跡跟蹤的蒙特卡羅方法,對不同領域的二次電子倍增敏感區間進行預估和相關分析,但大部分工作并未考慮二次電子倍增過程中的空間電荷效應,因此無法獲得完整的物理圖像和深入認識[5?9].Gopinath等[10]首次使用粒子模擬方法,驗證了Kishek動力學理論模型所得雙平板二次電子倍增的相關規律.Riyopoulos[11]則單獨討論了空間電荷效應對雙邊二次電子倍增的影響.上述大多數研究工作均是針對低階(一階)模式下的雙邊二次電子倍增物理過程開展的,對于高階模式二次電子倍增方面的研究,尤其是其形成機理及瞬時演化與飽和特性方面的研究工作少有報道.

本文關注的是加速器動態建場中二次電子倍增的建立和維持過程[12?14],由于加速器動態建場過程中射頻腔內的電壓是由低到高建立的,因此腔體內的雙邊二次電子倍增過程將會經歷高階模式到低階模式的轉變.為評估高階模式二次電子倍增對加速器動態建場過程的影響,需要對高階模式二次電子倍增的形成機理和瞬態物理特性進行細致研究.本文采用粒子模擬(particle-in-cell,PIC)與蒙特卡羅(Monte-Carlo,MC)抽樣算法相結合的方法[15],從第一原理出發,對比研究了金屬無氧銅腔體一階與三階雙邊二次電子倍增過程不同的時域演化及飽和特性,分析了其不同的形成機制和作用機理.

2 物理模型

加速器動態建場環節中,腔內射頻電壓的建立是一個從無到有、逐步增長的過程,高Q值腔體(超導腔)需要較長的場加載時間,一般情況下為幾百個到數萬個射頻周期.因此,二次電子倍增形成后,其有足夠的時間發展到飽和階段.加速器建場過程中,若存在較為嚴重二次電子倍增現象,不僅會降低射頻系統的穩定性,甚至會導致建場失敗.如:超導直線加速器中的二次電子倍增行為會嚴重影響其運行穩定性;超導回旋加速器內,雜散場的存在將會引起較強的二次電子倍增效應,其可能導致射頻場的無法建立.

本文選用雙平板結構研究場加載過程中的二次電子倍增效應,一是因為實際的加速器腔體會出現類似的結構和場強分布,如pillbox腔主要工作模式TM010與雙平板場強分布形式基本相同,spoke腔和crab腔的場強分布也都類似于雙平板場強的分布形式;二是采用雙平板結構易于實現可計算物理建模,對實際復雜構型腔體的二次電子倍增過程進行模擬費時耗力,且不易俘獲二次電子倍增的細觀演化過程和發展飽和特性.不失一般性的前提下,采用雙平板簡化模型,并以此構型研究不同模式下的腔體雙邊二次電子倍增瞬時演化及飽和的全物理過程.

要研究加速器腔內建場與二次電子倍增的復雜非線性自洽互作用過程,必須建立外電路與二次電子倍增動力學耦合模型,將二次電子倍增作為外電路的一個動態負載器件,才能進行相關復雜物理過程的研究.本文采用“理想電壓源”(固定射頻電壓幅值)模型進行研究,目的是對問題進行簡化和分解,先闡明固定電壓幅值情況下腔體低階(一階)與高階(三階)模式雙邊二次電子倍增的形成機理和瞬態特性,奠定相關物理認識后,再考慮動態建場中的二次電子倍增高階模式向低階模式轉變的復雜非線性互作用物理過程.

建立的簡化模型如下:間距為L的腔體中,初始電子在射頻電壓VRF=VRF0sin(ωt+θ0)作用下(VRF0為射頻電壓幅值,ω=2πf,f為工作頻率,θ0為電子初始相位),從腔體左側壁面發射,經過半個射頻周期(T)的N倍(N為奇數)后獲得能量轟擊腔體右側壁面,激發出多于初始電子數目的二次電子,產生的二次電子同樣在射頻場作用下經過同樣時間轟擊腔體左側壁面,再次激發出更多的新的二次電子,如此往復,便會出現二次電子倍增效應(二次電子崩).

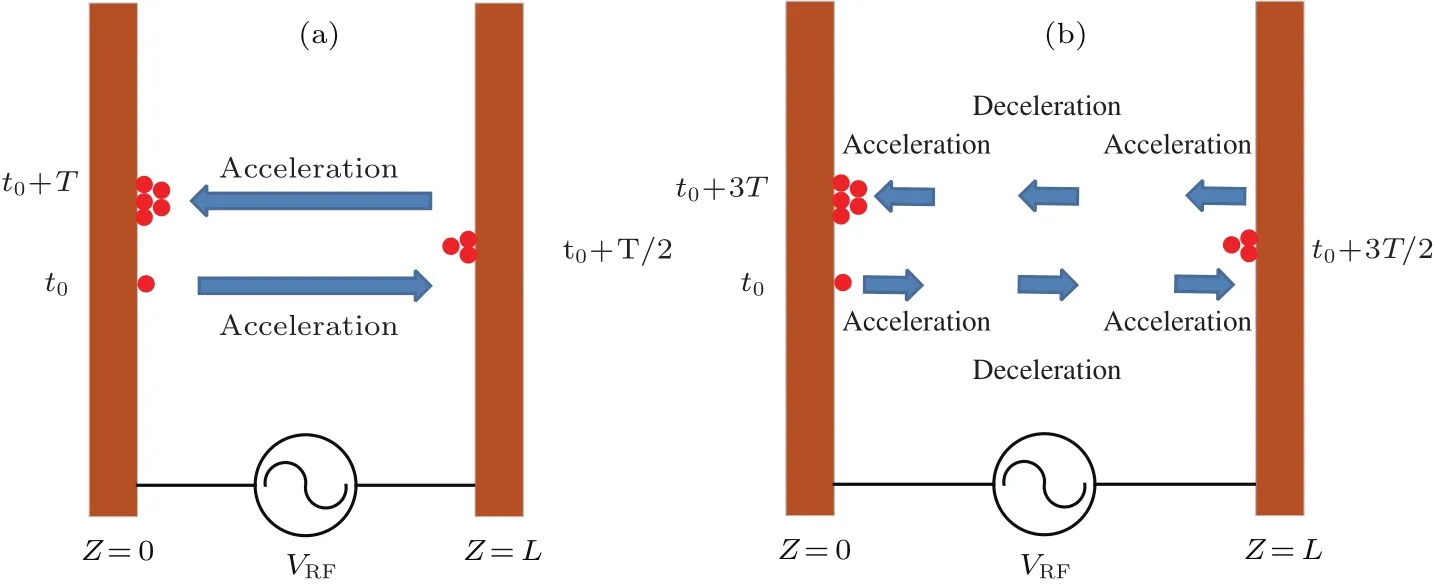
圖1 腔體雙邊二次電子倍增示意圖 (a)一階模式;(b)三階模式Fig.1.Schematic of two-sided multipactor discharge in cavity:(a)1st order mode;(b)3rd order mode.

由于雙邊二次電子倍增的相位聚焦條件滿足:0＜θ0＜tan?1(2/Nπ)(N為階數),因此階數越高要求電子的初始相位空間越窄.理論上雖然存在無數個高階模式,但是實際工程上考慮到三階模式的影響就足夠了.圖1給出了不同工作模式下的腔體雙邊二次電子倍增的示意圖,N=1為一階(低階)雙邊二次電子倍增,此模式電子在渡越過程中呈現持續加速的特性;N=3為三階(高階)雙邊二次電子倍增,此模式電子在渡越過程中呈現先加速后減速再加速的特性.

2.1 動力學方程與粒子模擬方法

模型中考慮了射頻場與帶電粒子產生的空間電荷場對粒子的雙重作用,暫未考慮腔體加載效應的影響(即尚未考慮射頻電壓幅值VRF0與外電路聯動的動態變化).

電子動力學方程如下:

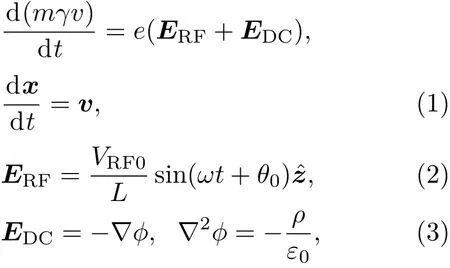
ERF,EDC分別為射頻電場強度矢量和電子產生的空間電荷場強度矢量;v,x,e和γ分別為電子速度矢量、位移矢量、電量和相對論因子;?,ρ分別為空間電荷靜電勢與電荷密度;?z為z方向單位矢量.EDC定義在網格中心,?,ρ定義在網格結點位置.使用cloud-in-cell(CIC)方法(線性插值PIC)將EDC權重到粒子位置,同樣方法將粒子電量權重到網格結點位置得出ρ.泊松方程可通過追趕法(一維情況)或松弛迭代求解(二維情況),?求解后,通過中心差分求解可得EDC.

編制了1D3V(一維三速)和2D3V(二維三速)PIC(粒子模擬)程序.由于1D3V程序計算速度遠快于2D3V程序,通過2D3V與1D3V程序模擬結果的比對,在完成1D3V程序正確性驗證后,主要使用1D3V-PIC程序對不同模式下的腔體雙邊二次電子倍增瞬時演化及飽和特性相關物理規律進行研究.

2.2 材料二次電子發射模型

采用Vaughan[16]提出的二次電子產額經驗擬合公式:

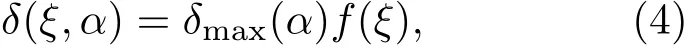
式中

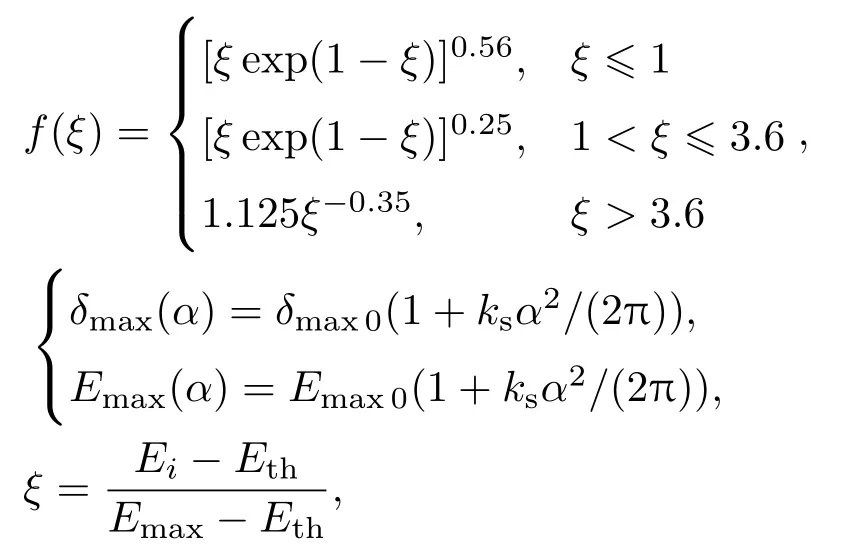
δ為二次電子產額(secondary electron yield,SEY)系數;δmax0為正入射二次電子產額系數最大值;Emax0為δmax0對應的入射能量;δmax(α)為斜入射二次電子產額系數最大值;Emax(α)為δmax(α)對應的入射能量;α為入射角(α=0為正入射,α=π/2為掠入射);ks為表面光滑系數(ks=0,1,2,分別代表粗糙,不光滑和光滑).Ei為電子碰撞能量;Eth為能量閾值,一般取Eth=12.5 eV.δ＞1對應的碰撞能量范圍(E1＜Ei＜E2,E1為二次電子倍增的碰撞能量下限值,E2為上限值)為材料的二次電子倍增區間,其代表此區間內每個種子電子碰撞產生的二次電子數目大于1.本文采用的是無氧銅材料(ks=1,δmax0=1.3,Emax0=600 eV),其正入射條件下的二次電子產額系數曲線如圖2所示.

圖2 無氧銅材料二次電子產額系數曲線(正入射條件下)Fig.2.Secondary electron emission yield coefficient(under normal incidence).

二次電子初始能量概率密度函數滿足[17]f(E0)=(E0/E20m)exp(?E0/E0m),其中,E0為二次電子出射能量,E0m是函數f(E0)峰值所對應的二次電子出射能量,E0m取值與材料特性有關,根據Vaughan的constant-k理論,一般取E0m=0.005Emax0.二次電子發射角?是偏離平行出射表面方向的角度,其概率密度函數g(?)滿足[17]g(?)=0.5sin?,?取值范圍0＜? ＜π.這里采用MC方法對二次電子的出射能量和角度進行隨機抽樣.

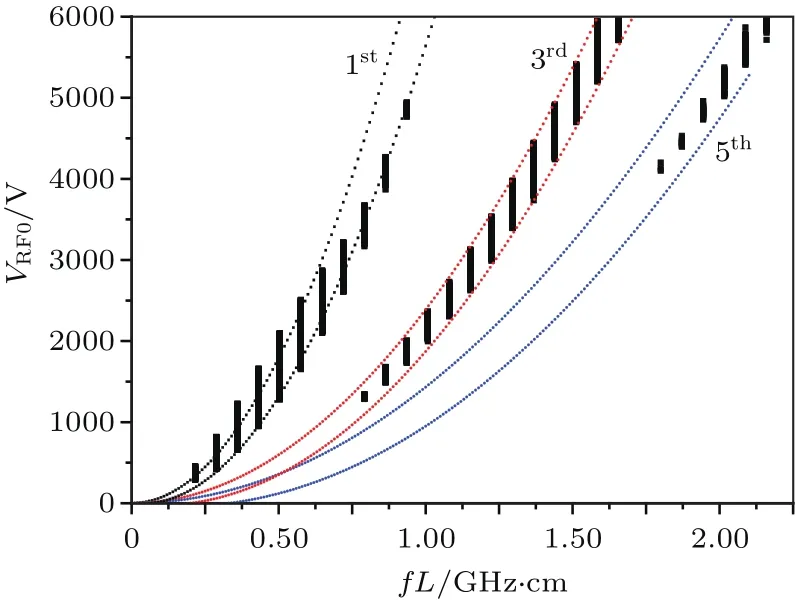
圖3 腔體雙邊二次電子倍增敏感區間Fig.3.Susceptibility of two-sided multipactor.

3 數值模擬結果

為了配合后續的實驗研究和相關驗證工作,粒子模擬中設置:射頻頻率f=72 MHz,腔體間距L=12 cm,對應頻率間距積fL=0.864 GHz·cm,二次電子倍增發生面積A=1.77 cm2,初始種子電子電流密度10μA/cm2(作用時間為射頻注入開始后的一個周期內,位置隨機出現在腔體左右兩側壁面).從圖3給出的雙邊二次電子倍增理論計算(曲線數據為理論計算結果)和蒙特卡羅模擬(黑點標識的數據為蒙特卡羅模擬結果)得到敏感區間,可以看出,低階(一階)二次電子倍增的射頻電壓幅值VRF0敏感區間在4 kV附近,高階(三階)二次電子倍增的射頻電壓幅值VRF0敏感區間在1.5 kV附近.由此可知,加速器腔體射頻建場的過程中,二次電子倍增勢必會經歷從高階到低階模式的轉換,高階和低階模式有何不同之處,需要進行細致的粒子模擬研究分析.分別設定VRF0=1600 V以及VRF0=4250 V,研究一階和三階二次電子倍增瞬態演化過程.這是因為在此電壓幅值下,兩種模式下的二次電子倍增飽和放電電流均可達到最大值.

圖4 二次電子數量隨時間演化關系Fig.4.Electron number vs.time.

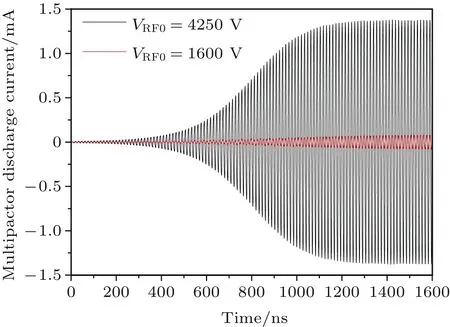
圖5 放電電流隨時間演化關系Fig.5.Discharge current vs.time.

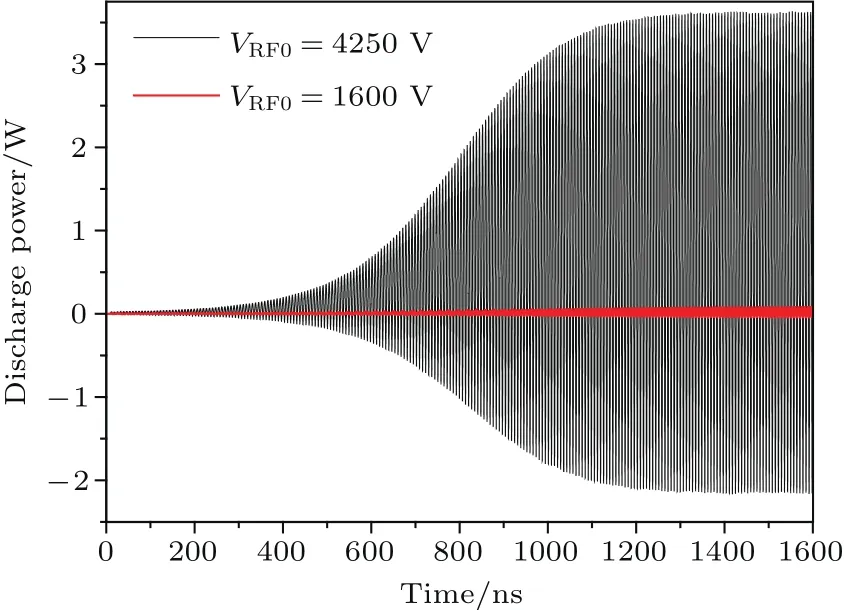
圖6 放電功率隨時間演化關系Fig.6.Discharge power vs.time.

首先,研究一階與三階模式二次電子倍增過程中二次電子數目、放電電流、放電和沉積功率等宏觀物理量時域演化特性.由圖4可以看出:二次電子數目隨時間以指數形式快速增長后趨于飽和振蕩.二次電子倍增發展階段,三階模式的二次電子數目增長率明顯低于一階模式;二次電子倍增飽和階段,三階模式的飽和二次電子數目明顯遠少于一階模式.從圖5可以看出,放電電流隨時間呈現指數式快速增長后趨于飽和并呈現穩定振蕩的狀態,放電電流與二次電子數目成正比關系.三階模式的放電電流明顯低于一階模式,起振時間明顯長于一階模式.圖6給出了放電功率(瞬時射頻電壓與瞬時放電電流的乘積)的時域演化過程.可以看出二次電子倍增過程中,并非呈現穩定的放電過程,而是存在較為明顯的部分充電過程,這是由于射頻場存在對部分電子減速現象引發的,尤其是在空間電荷效應較強的二次電子倍增飽和階段,三階模式放電功率的飽和值明顯小于一階模式.圖7給出了沉積功率(時間步長內所有電子碰撞壁面損失的能量除以時間步長后得到的數值)的時域演化過程.可以看出,沉積功率全部為正值,峰值沉積功率較峰值放電功率高出許多,這是由二次電子倍增的特殊物理過程決定的,放電功率發生在電子的渡越時間段,明顯長于沉積功率形成的碰撞時間段,根據能量守恒,峰值沉積功率必然高于峰值放電功率,三階模式沉積功率的飽和值明顯小于一階模式.對放電功率和沉積功率以射頻周期為單位進行平均,獲得了平均放電功率和平均沉積功率.從圖8可以看出,平均放電功率與平均沉積功率幾乎完全相等,電子從射頻源獲得的動能完全轉化為電子撞擊金屬壁面的沉積能量,三階模式的平均沉積功率和放電功率大約是一階模式1%的水平,這是由三階模式工作電壓以及放電電流均小于一階模式的雙重因素決定的.

其次,通過分析電子相空間、電荷密度以及平均二次電子產額、平均碰撞能量、放電電流、間隙電壓與二次電子數目的相互關系,研究一階與三階二次電子倍增的不同物理過程和作用機理.

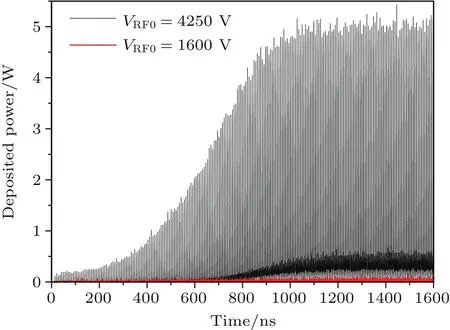
圖7 沉積功率隨時間演化關系Fig.7.Deposited power vs.time.

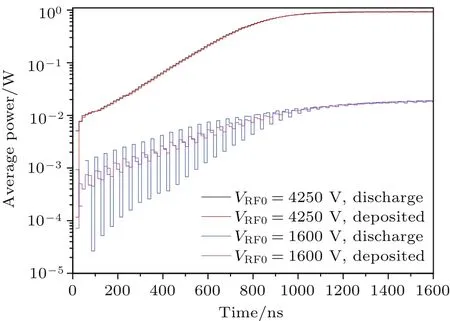
圖8 平均放電功率和沉積功率隨時間演化關系Fig.8.Average discharge power and average deposited power vs.time.

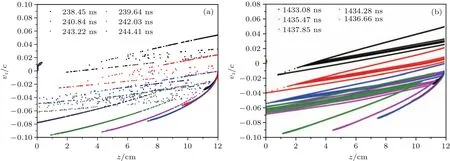
圖9 一階雙邊二次電子倍增模式下的電子相空間分布隨時間演化關系,c為真空中的光速 (a)二次電子倍增發展階段;(b)二次電子倍增飽和階段Fig.9.Electron phase-space distribution of 1st order two-sided multipactor in cavity,c is the speed of light in vacuum:(a)Development stage of multipactor;(b)saturation stage of multipactor.

如圖9—圖10所示,對于一階模式,二次電子從腔體壁面出射向對側壁面運動過程中,呈現單個電子束團加速的運動特性;對于三階模式,二次電子從腔體壁面出射向對側壁面運動過程中,呈現出加速-減速-加速的特征,并顯著存在多個電子束團相向運動的特性,這正是高階模式特有的電子渡越特性.一階與三階模式均存在電子出射速度雜散與空間電荷效應導致的電子束變寬效應.二次電子倍增發展階段,電子空間分布較窄,相空間上存在部分雜散電子;二次電子倍增飽和階段,空間電荷效應導致電子空間分布變寬,相空間上雜散電子數目明顯增加,此時的空間電荷效應較為強烈,電子間的排斥明顯.

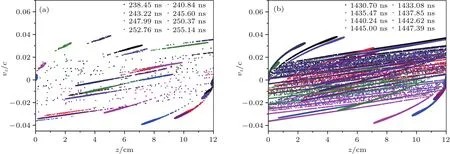
圖10 三階雙邊二次電子倍增模式下的電子相空間分布隨時間演化關系,c為真空中的光速 (a)二次電子倍增發展階段;(b)二次電子倍增飽和階段Fig.10.Electron phase-space distribution of 3rd order two-sided multipactor in cavity,c is the speed of light in vacuum:(a)Development stage of multipactor;(b)saturation stage of multipactor.

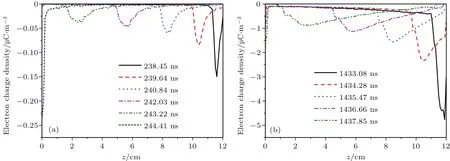
圖11 一階雙邊二次電子倍增模式下的電荷密度空間分布隨時間演化關系 (a)二次電子倍增發展階段;(b)二次電子倍增飽和階段Fig.11.Charge density distribution of 1st order two-sided multipactor in cavity:(a)Development stage of multipactor;(b)saturation stage of multipactor.

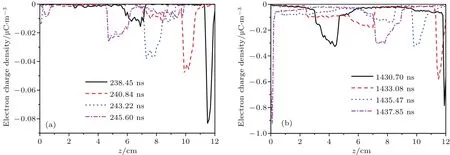
圖12 三階雙邊二次電子倍增模式下的電荷密度空間分布隨時間演化關系 (a)二次電子倍增發展階段;(b)二次電子倍增飽和階段Fig.12.Charge density distribution of 3rd order two-sided multipactor in cavity:(a)Development stage of multipactor;(b)saturation stage of multipactor.

如圖11—圖12所示,電荷密度最大值位于壁面位置附近,隨著遠離壁面距離的增加,電荷密度逐漸降低但空間分布逐漸變寬,這是不同出射速度電子在電場加速下速度分布向密度分布轉化的結果.二次電子倍增發展階段,電荷密度較低且其空間分布較窄;二次電子倍增飽和階段,電荷密度較高且其空間分布較寬.三階模式飽和階段的電荷密度明顯小于一階模式.

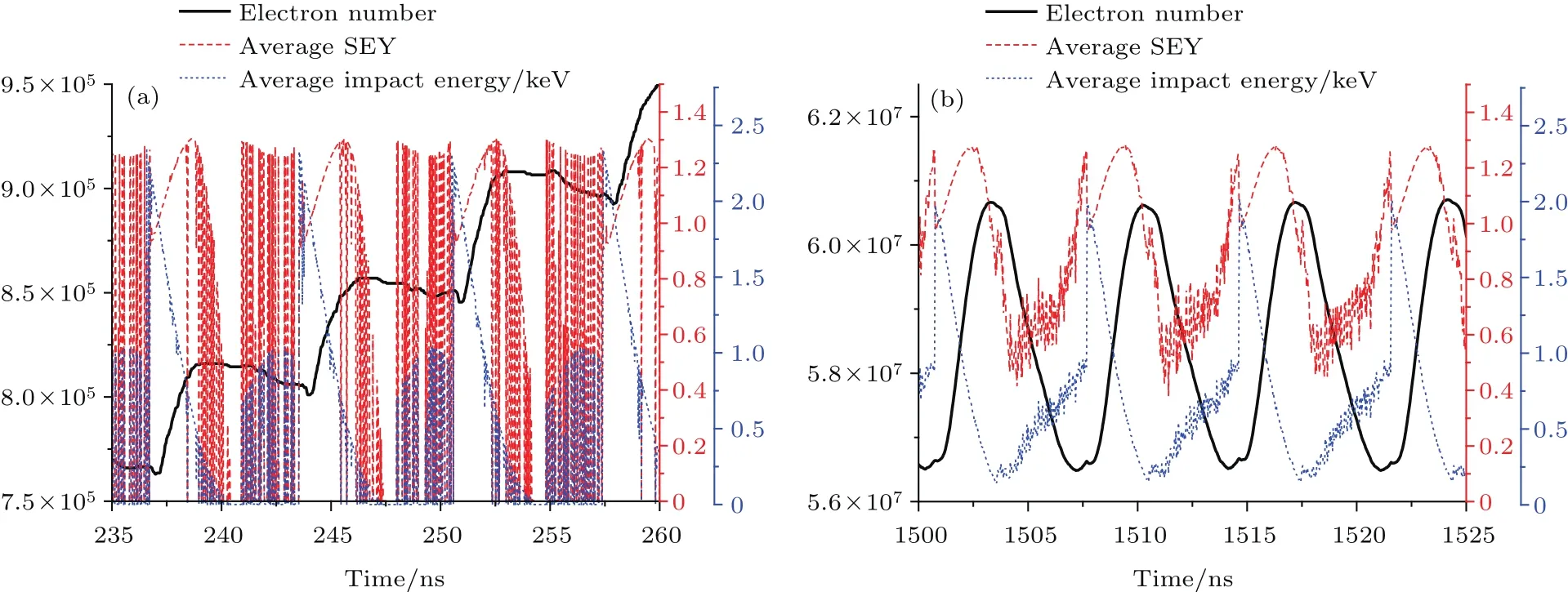
圖13 (網刊彩色)一階雙邊二次電子倍增模式下的電子數目、二次電子產額系數及碰撞能量隨時間演化關系 (a)二次電子倍增發展階段;(b)二次電子倍增飽和階段Fig.13.(color online)The evolution relationship of electron number,SEY coefficient and impact energy of 1st order two-sided multipactor in cavity:(a)Development stage of multipactor;(b)saturation stage of multipactor.

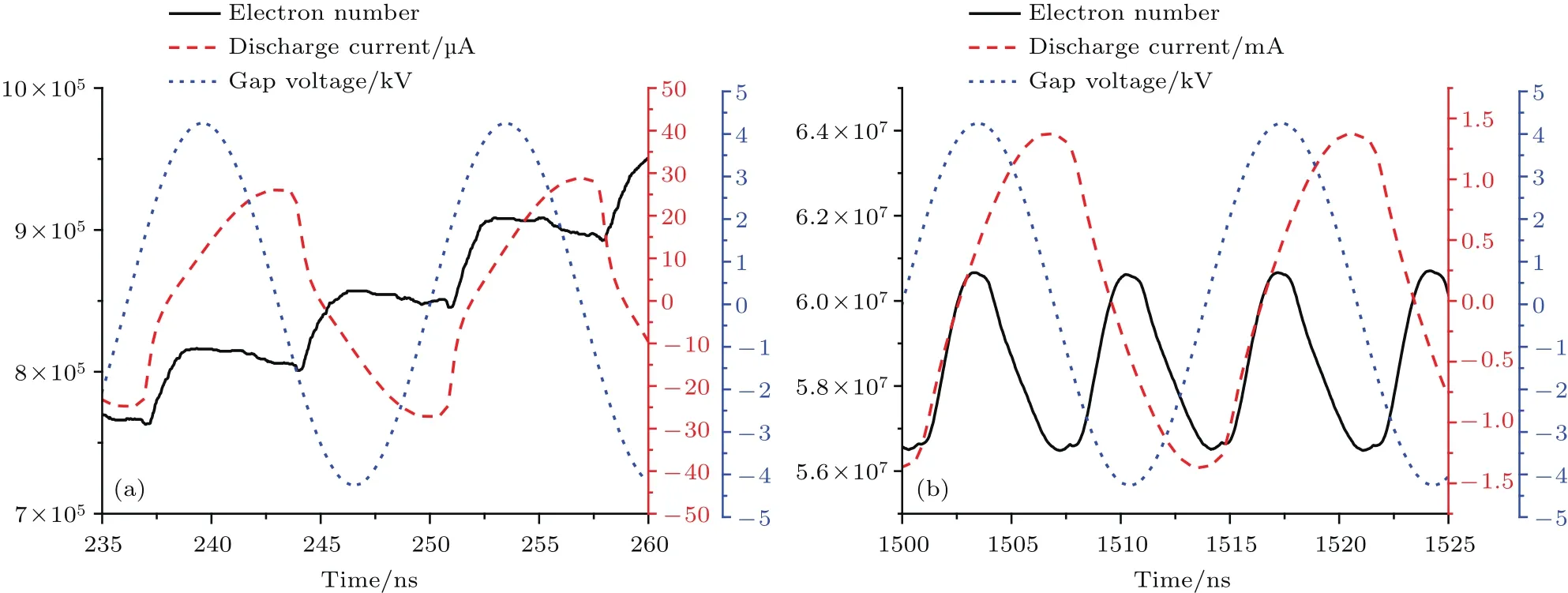
圖14 (網刊彩色)一階雙邊二次電子倍增模式下的電子數目、間隙電壓及放電電流隨時間演化關系 (a)二次電子倍增發展階段;(b)二次電子倍增飽和階段Fig.14.(color online)The evolution relationship of electron number,gap voltage and discharge current of 1st order two-sided multipactor in cavity:(a)Development stage of multipactor;(b)saturation stage of multipactor.

圖13—圖15給出了一階雙邊二次電子倍增模式發展與飽和階段各特征物理量的時域演化關系.可以看出,二次電子倍增過程中,放電電流波形較間隙射頻電壓波形存在明顯的延時效應,放電電流振蕩周期與射頻周期相等.二次電子倍增發展階段,由于空間電荷效應不明顯,電子數目呈現臺階式的指數快速增長,陡直上升沿對應絕大多數高能電子碰撞壁面引發二次電子倍增時刻,平直段為大多數電子在間隙內渡越的時段,平直段的持續時間(間隙電子渡越時間)約為半個射頻周期,電子數目平直段對應電子的持續渡越加速狀態,此時對應的放電電流呈現持續增加特性,周期內放電電流的最大值和最小值分別位于電子碰撞壁面時刻前后(碰壁前被加速的電子速度達到最大,碰壁后二次電子沿碰撞方向反方向出射,此時段放電電流時間變化率最大).隨著二次電子數目的快速增長,空間電荷效應逐漸顯著,二次電子倍增進入飽和階段,此時電子數目不再呈現指數增長,而是趨于穩定飽和狀態,并伴隨周期性振蕩,振蕩周期為半個射頻周期,二次電子倍增飽和階段,較強的空間電荷效應使得放電電流變化率明顯減小,放電電流最大值對應二次電子數目最小值,而放電電流最小值對應二次電子數目最大值.沉積功率振蕩周期等于半個射頻周期,當二次電子數目陡增上升前沿來臨時,電子沉積功率從零迅速增加到最大值;當二次電子數目達到射頻周期內最大值時電子沉積功率衰減為零;放電功率振蕩頻率為射頻頻率的2倍,放電功率由放電電流與射頻電壓的乘積決定,放電功率為負值的部分說明存在明顯的充電過程.

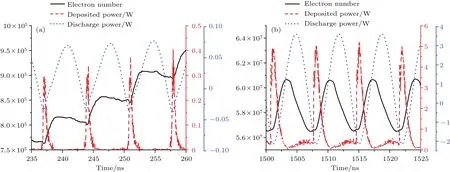
圖15 (網刊彩色)一階雙邊二次電子倍增模式下的電子數目、放電功率及沉積功率隨時間演化關系 (a)二次電子倍增發展階段;(b)二次電子倍增飽和階段Fig.15.(color online)The evolution relationship of electron number,discharge and deposited power of 1st order two-sided multipactor in cavity:(a)Development stage of multipactor;(b)saturation stage of multipactor.

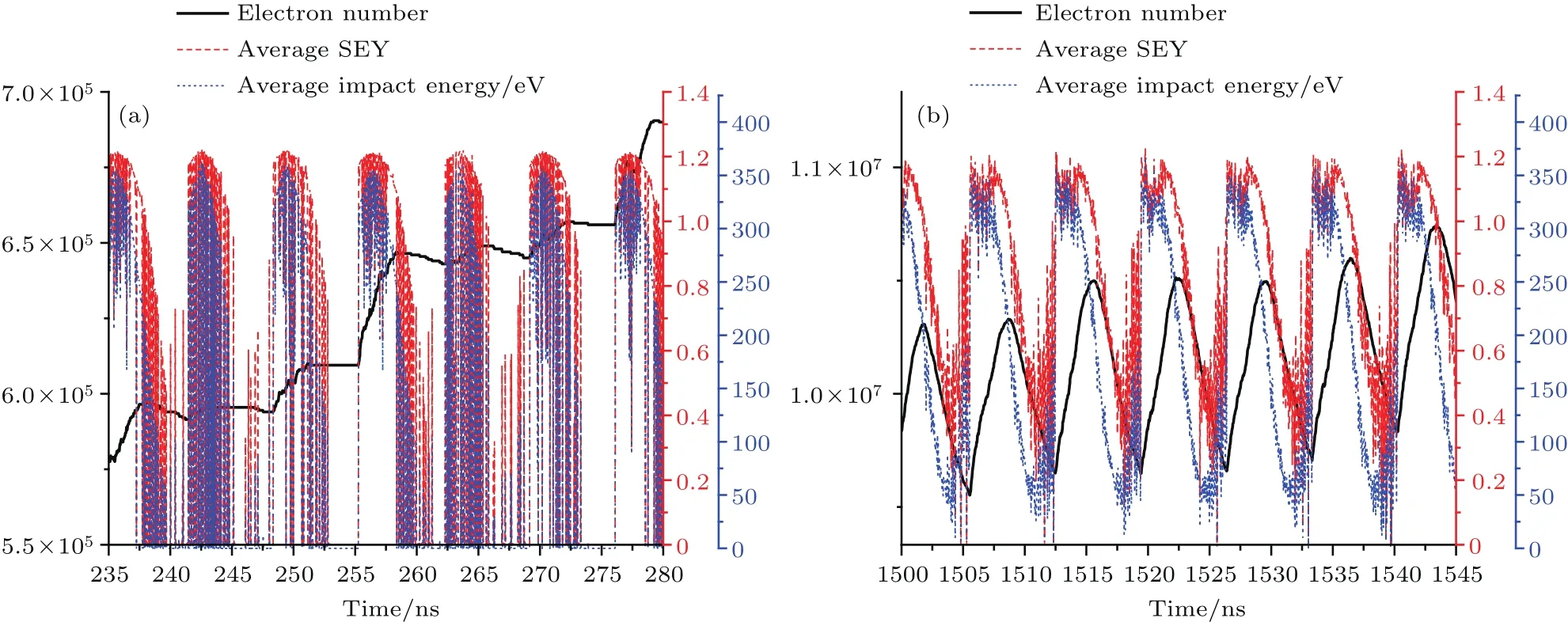
圖16 (網刊彩色)三階雙邊二次電子倍增模式下的電子數目、二次電子產額系數及碰撞能量隨時間演化關系 (a)二次電子倍增發展階段;(b)二次電子倍增飽和階段Fig.16.(color online)The evolution relationship of electron number,SEY coefficient and impact energy of 3rd order two-sided multipactor in cavity:(a)Development stage of multipactor;(b)saturation stage of multipactor.

圖16—圖18給出了三階雙邊二次電子倍增模式發展與飽和階段各特征物理量的時域演化關系,可以看出:二次電子倍增發展階段,由于空間電荷效應不明顯,電子數目呈現臺階式的指數快速增長,陡直的上升沿對應絕大多數高能電子碰撞壁面引發二次電子倍增時刻,平直段為大多數電子在間隙內渡越的時段,平直段的持續時間約為1.5個射頻周期.隨著二次電子數目的快速增長,空間電荷效應逐漸顯著,二次電子倍增進入飽和階段,此時電子數目不再呈現指數增長,而是趨于穩定飽和狀態,并伴隨周期性振蕩,振蕩周期為半個射頻周期.三階模式二次電子數目平直段持續時間(間隙電子渡越時間)是一階模式的3倍,導致三階模式二次電子增長率明顯低于一階模式.放電電流波形較間隙射頻電壓波形同樣存在明顯的延時效應.二次電子倍增發展階段,放電電流振蕩周期是射頻周期的3倍,由于電子數目平直段對應電子渡越的加速減速加速狀態,所以電子數目平直段對應的放電電流增加-減小-增加的特性;二次電子倍增飽和階段,在較強的空間電荷場作用下,其特性與一階二次電子倍增飽和階段特性幾乎完全相同,放電電流振蕩周期等于射頻周期.二次電子倍增發展階段,沉積功率和放電功率的振蕩周期均等于1.5個射頻周期,二次電子倍增飽和階段,沉積功率和放電功率的振蕩周期為半個射頻周期;當二次電子數目陡增上升前沿來臨時,電子沉積功率從零迅速增加到最大值,當二次電子數目達到射頻周期內最大值時電子沉積功率衰減為零;相對一階模式,三階模式飽和時的沉積功率脈寬(脈沖前沿與脈沖后沿0.5倍峰值位置處兩點間的時間間隔)更寬.而放電功率同樣存在負值部分,說明三階二次電子倍增過程中同樣存在明顯的充電現象.

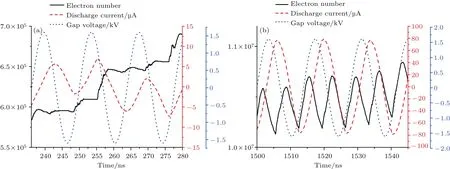
圖17 (網刊彩色)三階雙邊二次電子倍增模式下的電子數目、間隙電壓及放電電流隨時間演化關系 (a)二次電子倍增發展階段;(b)二次電子倍增飽和階段Fig.17.(color online)The evolution relationship of electron number,gap voltage and discharge current of 3rd order two-sided multipactor in cavity:(a)Development stage of multipactor;(b)saturation stage of multipactor.

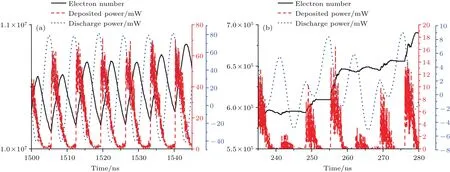
圖18 (網刊彩色)三階雙邊二次電子倍增模式下的電子數目、放電功率及沉積功率隨時間演化關系 (a)二次電子倍增發展階段;(b)二次電子倍增飽和階段Fig.18.(color online)The evolution relationship of electron number,discharge and deposited power of 3rd order two-sided multipactor in cavity:(a)Development stage of multipactor;(b)saturation stage of multipactor.

4 結 論

面向加速器射頻腔動態建場中存在的二次電子倍增建立、維持和飽和過程,為有效評估高階模式二次電子倍增對加速器動態建場過程的影響,利用蒙特卡羅算法抽樣出射電子能量和角度、采用粒子模擬方法求解帶電粒子與射頻場及空間電荷場的互作用過程,對金屬無氧銅腔體雙邊二次電子倍增高階(三階)與低階(一階)模式的瞬時演化及飽和特性進行了細致的數值模擬對比研究.

數值模擬結果表明:二次電子倍增過程中,電子數目、放電電流、放電功率、沉積功率隨時間呈現以指數形式快速增長后趨于飽和振蕩的規律,相對一階模式,三階模式飽和值更小且到達飽和值的上升時間更長.放電電流相對腔體射頻電壓存在延時現象,導致二次電子倍增過程中存在充電過程.統計發現平均放電功率等于平均沉積功率,三階模式的放電功率大約是一階模式1%水平,因此加速器腔體從低電壓到高電壓(依次經歷二次電子倍增的高階和低階模式)的動態建場過程中高階模式的影響相對較小.二次電子倍增過程中,一階模式呈現單電子束團加速運動特性,三階模式則呈現加速/減速/加速及多電子束團相向運動的復雜特性.三階模式飽和階段電荷密度明顯低于一階模式,空間電荷效應小于一階模式.二次電子倍增形成發展階段,一階模式電子渡越時間約為半個射頻周期,放電電流振蕩周期與射頻周期相等;三階模式電子渡越時間約為1.5倍射頻周期,放電電流振蕩周期為射頻周期的3倍.二次電子飽和階段,在較強空間電荷效應作用下,三階與一階模式的特性趨于一致,即放電電流振蕩周期與射頻周期相等,放電功率和沉積功率振蕩頻率為射頻周期的2倍.此外,相對一階模式,三階模式飽和時的沉積功率脈寬更寬.

[1]Vaughan J R M 1988IEEE Trans.Electron Dev.35 1172

[2]Kishek R A,Lau Y Y,Ang L K,Valfells A,Gilgenbach R M 1998Phys.Plasmas5 2120

[3]Kishek R A,Lau Y Y 1995Phys.Rev.Lett.75 1218

[4]Kishek R A 2012Phys.Rev.Lett.108 035003

[5]Zhang P,Lau Y Y,Franzi M,Gilgenbach R M 2011Phys.Plasmas18 053508

[6]Sazontov A G,Nechaev V E,Vdovicheva N K 2011Appl.Phys.Lett.98 161503

[7]Sazontov A,Buyanova M,Semenov V,Rakova E,Vdovicheva N,Anderson D,Lisak M,Puech J,Lapierre L 2005Phys.Plasmas12 053102

[8]Zhang X,Wang Y,Fan J J 2015Phys.Plasmas22 022110

[9]Li Y D,Yan Y J,Lin S,Wang H G,Liu C L 2014Acta Phys.Sin.63 047902(in Chinese)[李永東,閆楊嬌,林舒,王洪廣,劉純亮2014物理學報63 047902]

[10]Gopinath V P,Verboncoeur J P,Birdsall C K 1998Phys.Plasmas5 1535

[11]Riyopoulos S 1997Phys.Plasmas4 1448

[12]Devanz G 2001Phys.Rev.Special Topics-Accelerators and Beams4 012001

[13]Xu B,Li Z Q,Sha P,Wang G W,Pan W M,He Y 2012High Power Laser and Particle Beams24 2723(in Chinese)[徐波,李中泉,沙鵬,王光偉,潘衛民,何源 2012強激光與粒子束24 2723]

[14]Wang C,Andreas Adelmann,Zhang T J,Jiang X D 2012High Power Laser and Particle Beams24 1244(in Chinese)[王川,Andreas Adelmann,張天爵,姜興東2012強激光與粒子束24 1244]

[15]Kim H C,Verboncoeur J P 2005Phys.Plasmas12 123504

[16]Vaughan J R M 1993IEEE Trans.Electron Dev.40 830

[17]Kishek R A,Lau Y Y 1998Phys.Rev.Lett.80 193

Comparison between the 1st and 3rd order mode temporal characteristics of two-sided multipactor discharge in cavity?

Dong Ye1)2)?Liu Qing-Xiang1)Pang Jian3)?Zhou Hai-Jing2)Dong Zhi-Wei2)

1)(School of Physical Science and Technology,Southwest Jiaotong University,Chengdu 610031,China)

2)(Institute of Applied Physics and Computational Mathematics,Beijing 100094,China)

3)(Institute of Fluid Physics,China Academy of Engineering Physics,Mianyang 621900,China)

10 May 2017;revised manuscript

6 July 2017)

For investigating the in fl uence of high order two-sided multipactor discharge on the accelerator fi eld-building process,the temporal characteristics of the 3rd order two-sided multipactor discharge in oxygenfree copper cavity are studied numerically.The particle-in-cell and Monte-Carlo methods are used in the simulation and the characteristics of the 1st order mode are also studied for comparison.The numerical results can be concluded as follows.In the multipactor discharge evolution,the electron number,discharge current,deposited and discharge power increase exponentially and tend to be saturated.At the saturation stage of the 3rd order mode,the values of electron number,discharge current,deposited and discharge power are lower than at the saturation stage of the 1st order mode.Meanwhile,the rising time of waveform in the 3rd order mode is longer than in the 1st order mode.There is a time-delay phenomenon in the waveform of discharge current,which results in a partial charging process in multipactor discharge.The average value of the discharge power is equal to the average deposited power.The value of discharge power in the 3rd order mode is about 1%of that in the 1st order mode.Therefore,the 3rd order mode is not signi fi cant in accelerator fi eld-building process compared with the 1st order mode.The characteristic of the 1st order two-sided multipactor discharge is the accelerated motion of single electron beam,while that of the 3rd order is the complex accelerated-decelerated-accelerated motion of multi-electron beams.When the multipactor discharge enters into the saturation stage,the space charge e ff ect of the 3rd order mode is not stronger than that of 1st order mode.

two-sided multipactor,temporal evolution,Monte-Carlo method,particle-in-cell method

(2017年5月10日收到;2017年7月6日收到修改稿)

10.7498/aps.66.207901

?國家自然科學基金(批準號:11475155,11305015)資助的課題.

?通信作者.E-mail:dongye0682@sina.com

?通信作者.E-mail:jpang@mail.ustc.edu.cn

?2017中國物理學會Chinese Physical Society

http://wulixb.iphy.ac.cn

PACS:79.20.Hx,52.80.Pi,52.65.Rr,52.65.PpDOI:10.7498/aps.66.207901

*Project supported by the National Natural Science Foundation of China(Grant Nos.11475155,11305015).

?Corresponding author.E-mail:dongye0682@sina.com

?Corresponding author.E-mail:jpang@mail.ustc.edu.cn