基于格林函數(shù)法的奇型Mathieu-Gaussian光束?

吳瓊 任志君 杜林岳 胡海華 顧穎楊朝鳳

1)(浙江師范大學(xué)信息光學(xué)研究所,金華 321004)

2)(浙江師范大學(xué),浙江省光信息檢測(cè)與顯示技術(shù)研究重點(diǎn)實(shí)驗(yàn)室,金華 321004)

基于格林函數(shù)法的奇型Mathieu-Gaussian光束?

吳瓊1)2)?任志君1)2)杜林岳1)2)胡海華1)2)顧穎2)楊朝鳳2)

1)(浙江師范大學(xué)信息光學(xué)研究所,金華 321004)

2)(浙江師范大學(xué),浙江省光信息檢測(cè)與顯示技術(shù)研究重點(diǎn)實(shí)驗(yàn)室,金華 321004)

格林函數(shù)法,Mathieu-Gaussian光束,虛源點(diǎn)

根據(jù)光束傳播的獨(dú)立性和疊加性原理,引入了一組能夠產(chǎn)生第一類(2n+2階)奇型Mathieu-Gaussian光束的虛光源點(diǎn).利用虛源點(diǎn)技術(shù)和格林函數(shù)法,計(jì)算得到第一類奇型Mathieu-Gaussian光束的嚴(yán)格解析積分表達(dá)式.利用該表達(dá)式得到了軸上光場(chǎng)分布的積分解析解.以三階非旁軸修正為例,得到了第一類奇型Mathieu-Gaussian光束保留到三階非旁軸修正項(xiàng)的軸上光場(chǎng)分布精確解.

1 引 言

無衍射光束是滿足波動(dòng)方程的一種特殊本征模式.無衍射傳輸模式的特殊之處在于其分布與傳輸距離無關(guān),因而在傳播過程中,垂直于傳播方向的截面光強(qiáng)分布處處不變,即光束不會(huì)發(fā)生衍射.1987年,Durnin找到并產(chǎn)生了第一個(gè)可實(shí)用的無衍射光束——Bessel光束[1,2].由于無衍射Bessel光束在傳輸過程中形態(tài)不變,因此在產(chǎn)生后廣泛應(yīng)用于科學(xué)實(shí)驗(yàn),比如光通信和檢測(cè)[3]、激光打孔或準(zhǔn)直[4]、醫(yī)學(xué)成像[5,6]、微觀粒子的俘獲和操縱[7].需要指出的是,無衍射Bessel光束只是一個(gè)理論模型,就像實(shí)際并不存在理想的余弦波一樣,實(shí)際使用的Bessel光束均是剪切過的有限能量的準(zhǔn)無衍射Bessel光束[3?7].

除無衍射Bessel光束之外,Gutiérrez-Vega等通過進(jìn)一步的研究指出,在不同坐標(biāo)系下的波動(dòng)方程傳輸不變(無衍射)特解有四種形式,分別為直角坐標(biāo)系下的Cosine光束、極坐標(biāo)系下的Bessel光束、橢圓坐標(biāo)系下的Mathieu光束[8?10],以及拋物坐標(biāo)系下的Parabolic光束[11,12].對(duì)于橢圓坐標(biāo)系下的無衍射Mathieu光束,在數(shù)學(xué)上描述它的Mathieu函數(shù)比描述Cosine光束和Bessel光束的Cosine函數(shù)和Bessel函數(shù)復(fù)雜得多,其光學(xué)形態(tài)也豐富得多.與Cosine函數(shù)和Bessel函數(shù)類似,Mathieu函數(shù)并不能平方可積,這意味著理想Mathieu光束有無窮大的能量.顯然,理想Mathieu光束僅僅是一個(gè)理論模型,實(shí)際中常使用被Gaussian函數(shù)剪切的、具有準(zhǔn)無衍射傳輸特性的Mathieu-Gaussian光束[13?15].研究Mathieu-Gaussian光束的傳輸更具實(shí)際意義.

光束的傳輸問題本質(zhì)上是衍射問題.Born和Wolf指出,“衍射問題是光學(xué)中遇到的最困難的問題之一,在衍射理論中,那種在某種意義上可以認(rèn)為是嚴(yán)格的解,是很少有的”,“對(duì)少數(shù)其他衍射問題也求得了嚴(yán)格解.但是,由于數(shù)學(xué)上的困難,在大多數(shù)有實(shí)際意義的情況中,還必須采用近似方法”.近似方法只能處理滿足某種近似條件的光束傳輸問題,比如旁軸光學(xué)問題.對(duì)于光束傳輸?shù)娜我馇闆r,特別是非旁軸情況,近似法不能給出正確結(jié)果.

在隨后的研究中,人們發(fā)現(xiàn)在構(gòu)建虛源點(diǎn)基礎(chǔ)上[16?18],利用格林函數(shù)法[19?22],可研究某些光束的非旁軸傳輸.對(duì)于光束的傳輸(衍射)問題,虛源點(diǎn)技術(shù)將初始光束分解成很多點(diǎn)源的疊加,如果知道每個(gè)點(diǎn)源產(chǎn)生的場(chǎng)分布,利用光束的疊加原理,即可求出光束傳輸過程的場(chǎng)分布,這種方法稱為格林函數(shù)法.點(diǎn)源產(chǎn)生的場(chǎng)叫作格林函數(shù).到目前為止,通過構(gòu)建虛源點(diǎn),利用格林函數(shù)法,已經(jīng)研究了多種具有實(shí)用價(jià)值的光束的傳播,包括幾類準(zhǔn)無衍射光束的傳播,比如Laguerre-Gaussian光束[19],Bessel-Gaussian光束[20],Elegant Hermite-Laguerre-Gaussian光束[21],Pearcey光束[22].然而,由于橢圓坐標(biāo)系下Mathieu函數(shù)的復(fù)雜性,至今還未見通過構(gòu)建虛源點(diǎn),利用格林函數(shù)法研究Mathieu-Gaussian光束的報(bào)道.

以第一類奇型Mathieu-Gaussian光束為例,首先根據(jù)光束傳輸?shù)莫?dú)立性和疊加性原理,將Mathieu-Gaussian光束分解為不同階次的Bessel光束無窮項(xiàng)求和的形式.然后,通過構(gòu)建虛源點(diǎn),利用格林函數(shù)法理論推導(dǎo)得到Mathieu-Gaussian光束傳輸?shù)慕馕龇e分表達(dá)式.根據(jù)該積分表達(dá)式,得到Mathieu-Gaussian光束在軸上光場(chǎng)的三階非旁軸修正.研究結(jié)論進(jìn)一步說明了格林函數(shù)法在研究光束旁軸與非旁軸傳輸方面的重要作用.

2 理 論

在橢圓坐標(biāo)系下描述Mathieu光束,形式最為簡(jiǎn)單直接[8?10]. 在橢圓坐標(biāo)系(ξ,η)下,Mathieu光束有四種類型,分別為第一、第二類奇型Mathieu光束和第一、第二類偶型Mathieu光束.第一、第二類奇型Mathieu光束即se2n+2(η,q)Jo2n+2(ξ,q)和se2n+1(η,q)Jo2n+1(ξ,q),n=1,2,3,···,se和Jo分別為奇型角向和奇型徑向Mathieu光束;第一、第二類偶型Mathieu光束即ce2n(η,q)Je2n(ξ,q)和ce2n+1(η,q)Je2n+1(ξ,q),n= 0,1,2,···,ce和Je分別為偶型角向和偶型徑向Mathieu光束[13?15,23?25].

相對(duì)于人們熟知的直角坐標(biāo)和極坐標(biāo),橢圓坐標(biāo)系很少使用,數(shù)學(xué)上也較難理解.為此,根據(jù)光束傳輸?shù)莫?dú)立性和疊加性原理,與文獻(xiàn)[13—15,23—25]所采用的數(shù)學(xué)手段類似,我們?nèi)圆捎眉?jí)數(shù)展開的方式,將Mathieu函數(shù)展開為極坐標(biāo)系的形式.兩類奇型Mathieu光束可分別展開為[13?15,23?25]

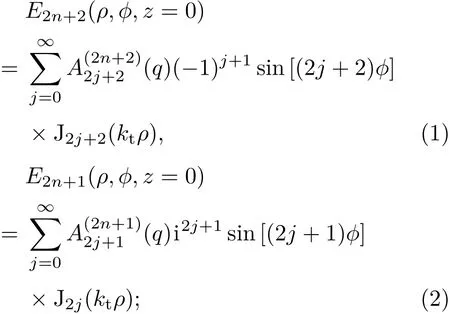
兩類偶型Mathieu光束可分別展開為

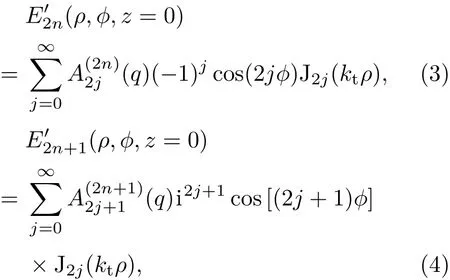
式中ρ,?,z為圓柱坐標(biāo)系下的位置變量;kt為光束的徑向分量;J2j(·)和J2j+2(·)分別表示2j階和2j+2階第一類Bessel函數(shù);q為橢圓參數(shù),,h為對(duì)應(yīng)橢圓兩焦點(diǎn)間的距離;為Mathieu函數(shù)的展開系數(shù)[14].

由(1)—(4)式可知,根據(jù)光束傳播的獨(dú)立性和疊加性原理,在圓柱坐標(biāo)系下,Mathieu-Gaussian光束能夠展開為不同階數(shù)的Bessel光束的無窮項(xiàng)求和的形式.這為我們避開橢圓坐標(biāo)系下復(fù)雜的Mathieu函數(shù)運(yùn)算,借助較為成熟簡(jiǎn)單的Bessel函數(shù)的性質(zhì),在圓柱坐標(biāo)系下研究Mathieu-Gaussian光束的傳輸特性,提供了一個(gè)很好的思路.典型地,以第一類奇型Mathieu-Gaussian光束(即2n+2階奇型Mathieu-Gaussian光束)作為研究對(duì)象,其在z=0平面的場(chǎng)分布為[13?15]

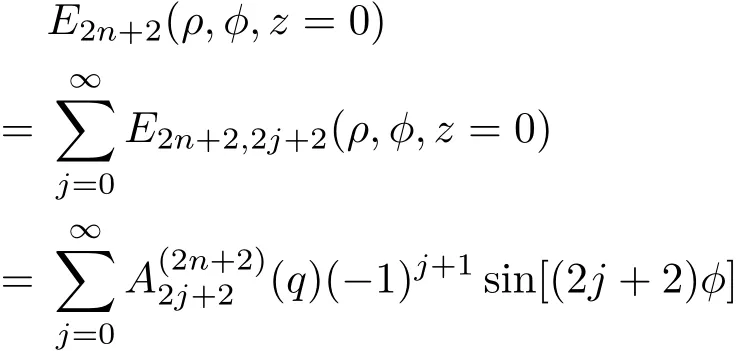
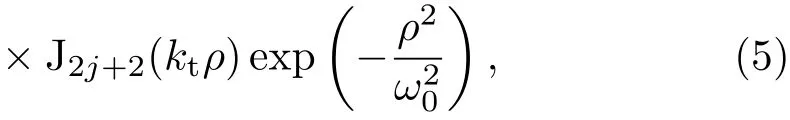
式 中2n+2(n=0,1,2,···)為奇型Mathieu-Gaussian光束的階數(shù),ω0為z=0平面上光束的束腰寬度.

在極坐標(biāo)系下,標(biāo)量波函數(shù)E(ρ,?,z)作為標(biāo)量波動(dòng)函數(shù),能夠產(chǎn)生沿z軸正方向(在z＞0的物理空間)傳播的第一類奇型Mathieu-Gaussian光束,且滿足齊次亥姆霍茲方程.既然Mathieu函數(shù)可在極坐標(biāo)系下展開[13?15,23],根據(jù)虛源技術(shù),假設(shè)有一系列強(qiáng)度為Scs(2j+2),位于z=zcs,半徑ρ=ρcs,并帶有一個(gè)方位角變量sin[(2j+2)?]的電環(huán),能夠產(chǎn)生第一類奇型Mathieu-Gaussian光束.只要選取合適的參量Scs(2j),zcs和ρcs,即可得到所需Mathieu-Gaussian光束.在極坐標(biāo)系下,設(shè)虛光源的標(biāo)量波函數(shù)E(ρ,?,z)為

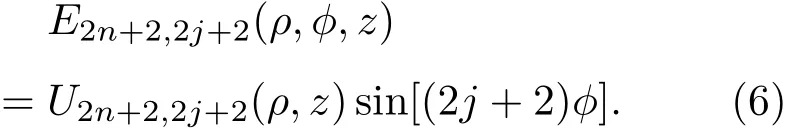
當(dāng)標(biāo)量波函數(shù)E2n+2,2j+2(ρ,?,z)為第一類奇型近旁軸Mathieu-Gaussian波函數(shù)時(shí),U2n+2,2j+2(ρ,z)滿足非齊次亥姆霍茲方程

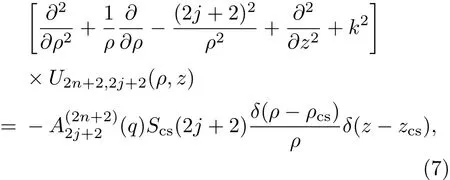
利用極坐標(biāo)系下的傅里葉-貝塞爾變換可得

由(7)式可得關(guān)于U2n+2,2j+2(ρ,z)的光譜2n+2,2j+2(η,z)的微分方程,將2n,2j(ρ,z)代入(8)式,有

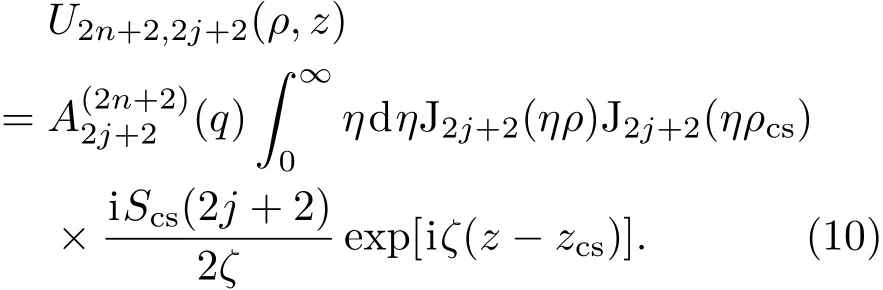
當(dāng)Re(z?zcs)＞0時(shí),有.現(xiàn)利用標(biāo)準(zhǔn)旁軸表述,在旁軸條件η2?k2限制下,將ζ展開為關(guān)于小量η2的級(jí)數(shù),保留其首項(xiàng)k作為振幅因子,保留其前兩項(xiàng)作為相位因子.在上述近似條件下,(10)式化簡(jiǎn)為

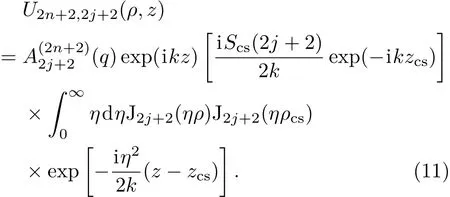
計(jì)算(11)式的積分,可以得到

為了在z＞0處獲得第一類奇型Mathieu-Gaussian光束,假設(shè)在邊界z=0處,在旁軸近似下,入射場(chǎng)分布由(5)式給出.通過比較(5)式與(12)式在z=0處的場(chǎng)分布,可以得到參量Scs(2j+2),zcs和ρcs為

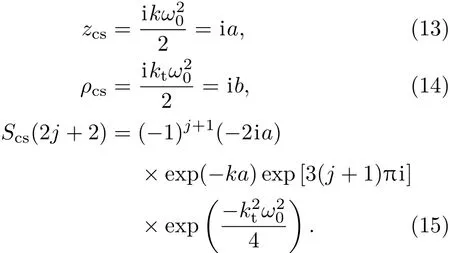
將(13)—(15)式代入(12)式, 得到關(guān)于U2n+2,2j+2(ρ,z)的旁軸近似解為

式中U2n+2,2j+2,p的下標(biāo)p表示旁軸近似. 此外, 將(13)—(15)式代入(10)式, 得到關(guān)于U2n+2,2j+2(ρ,z)的精確解的積分表達(dá)式為

結(jié)合(6)式和(16)式,得到旁軸條件下的第一類奇型Mathieu-Gaussian光束.結(jié)合(6)式和(17)式,可得第一類奇型Mathieu-Gaussian光束的光波傳輸場(chǎng).根據(jù)(13)式和(15)式,我們發(fā)現(xiàn)(7)式給出的光源位于z＞0處.(17)式給出的結(jié)果即為求解與(7)式相關(guān)的齊次亥姆霍茲方程,得到的Mathieu-Gaussian光束在自由空間傳輸?shù)木_解析積分表達(dá)式.不難看出,積分表達(dá)式((17)式)包含了低階旁軸近似解((16)式)和所有更高階的所謂非旁軸項(xiàng)(如倏逝波一樣).

運(yùn)用格林函數(shù)法,進(jìn)一步研究第一類奇型Mathieu-Gaussian光束傳輸?shù)慕馕霰磉_(dá)式.格林函數(shù)的微分方程為

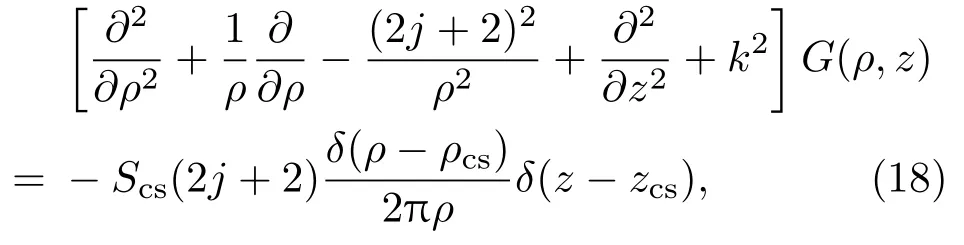
其中

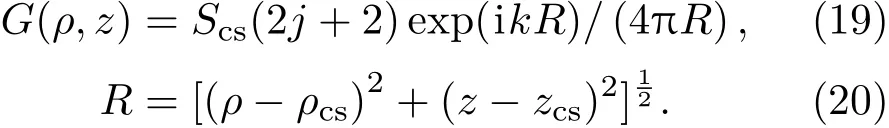
(18)式等號(hào)兩邊同乘以sin[(2j+2)?cs]且對(duì)?cs積分,積分區(qū)間為[0,2π],結(jié)合(13)—(15)式,且與(7)式進(jìn)行比較,可得

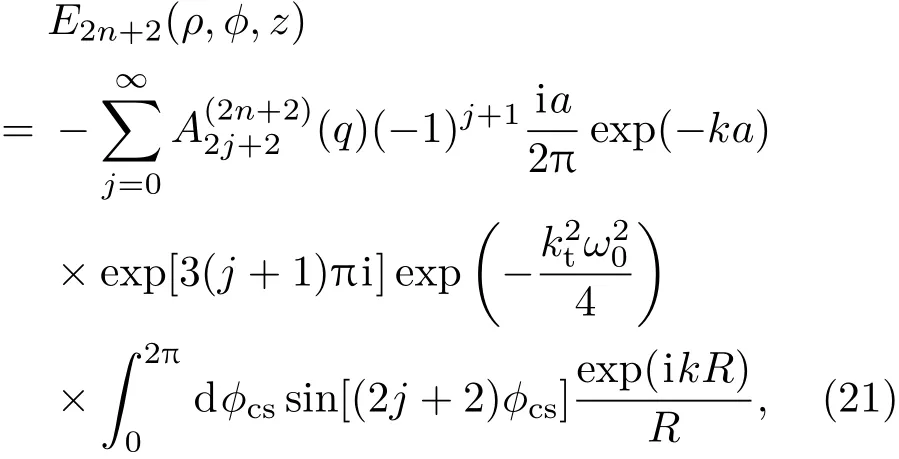
其中

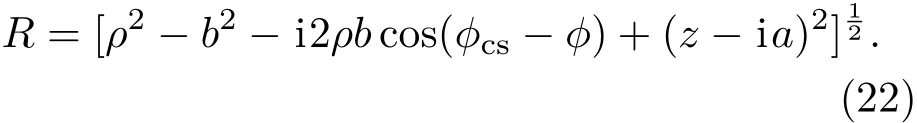
由(5)式,(11)式和(21)式可知,ρ變化的度規(guī)長度是ω0,η的變化范圍是0—1/ω0的數(shù)量級(jí)范圍.如果光束束腰寬度ω0遠(yuǎn)大于波長λ=2π/k,可以得到η2?k2,這與前述得到的旁軸近似解的條件相同.顯然,實(shí)現(xiàn)旁軸近似的要求,就是光束寬度必須比波長大.對(duì)大多數(shù)光束來說,這是容易滿足的條件.這也是大多數(shù)光學(xué)問題能夠在旁軸近似條件下得到相對(duì)容易的處理并可得到基本正確的結(jié)果的原因.

我們將計(jì)算2n階奇型Mathieu-Gaussian光束軸上(ρ=0)光場(chǎng)的非旁軸修正項(xiàng).根據(jù)(6)式和(17)式,可以得到軸上光場(chǎng)的分布為

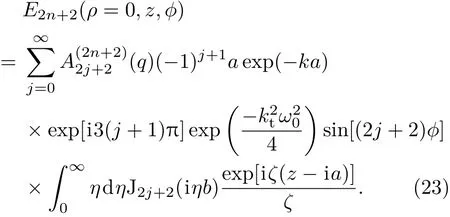
對(duì)(23)式中的振幅因子1/ζ和相位因子exp[iζ(z?ia)]作級(jí)數(shù)展開. 對(duì)于η2?k2的情況,兩者級(jí)數(shù)展開結(jié)果中,只有(kω0)?2m(m=0,1,2,···)及之前的項(xiàng)被保留,因而獲得m階修正項(xiàng).為了獲得軸上光場(chǎng)的三階非旁軸修正,此時(shí)m=3,即保留(kω0)?6及之前的項(xiàng).在這樣的展開結(jié)果下,將(23)式變形為

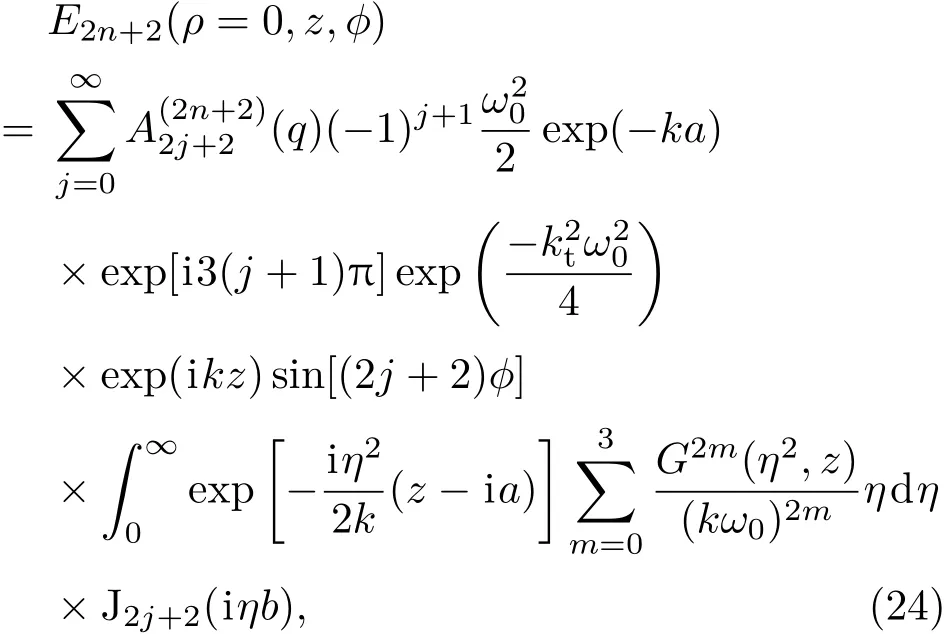
其中

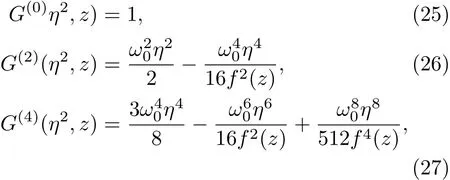
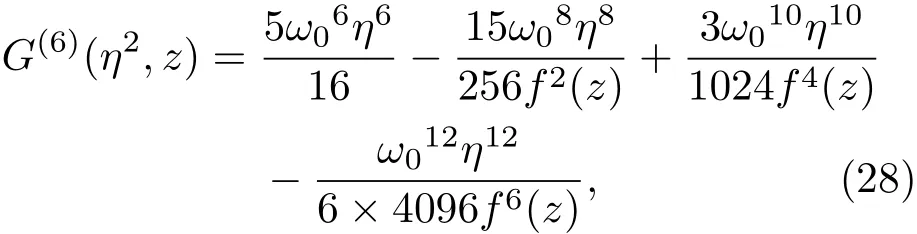
式中f2(z)=(1+iz/a)?1.

存在關(guān)系式

其中

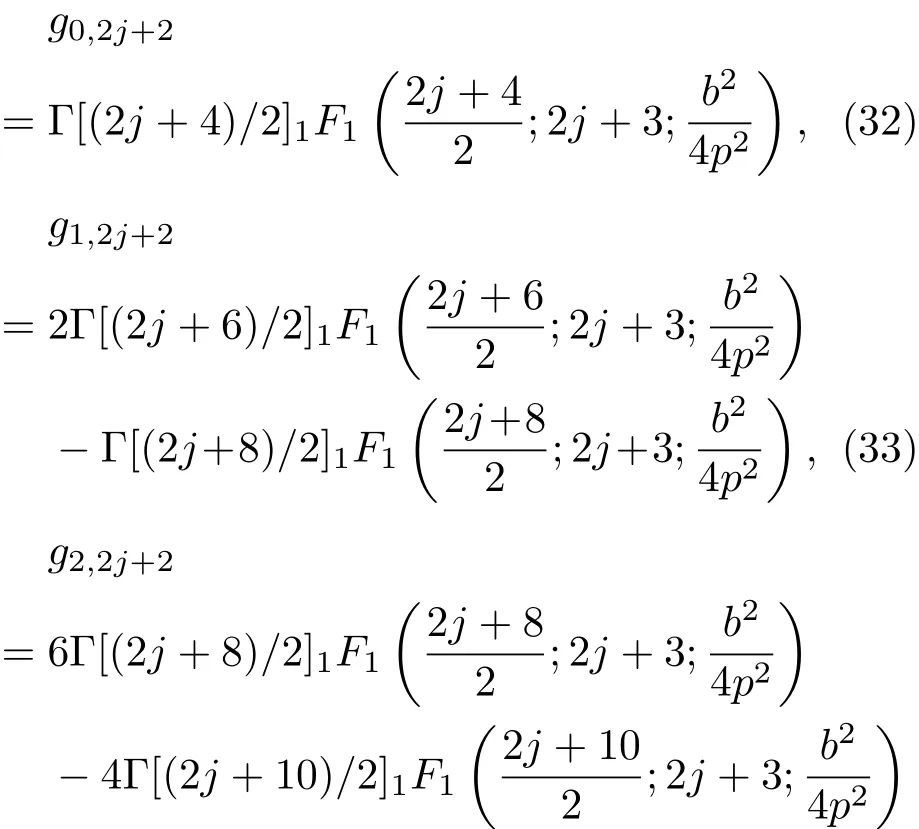
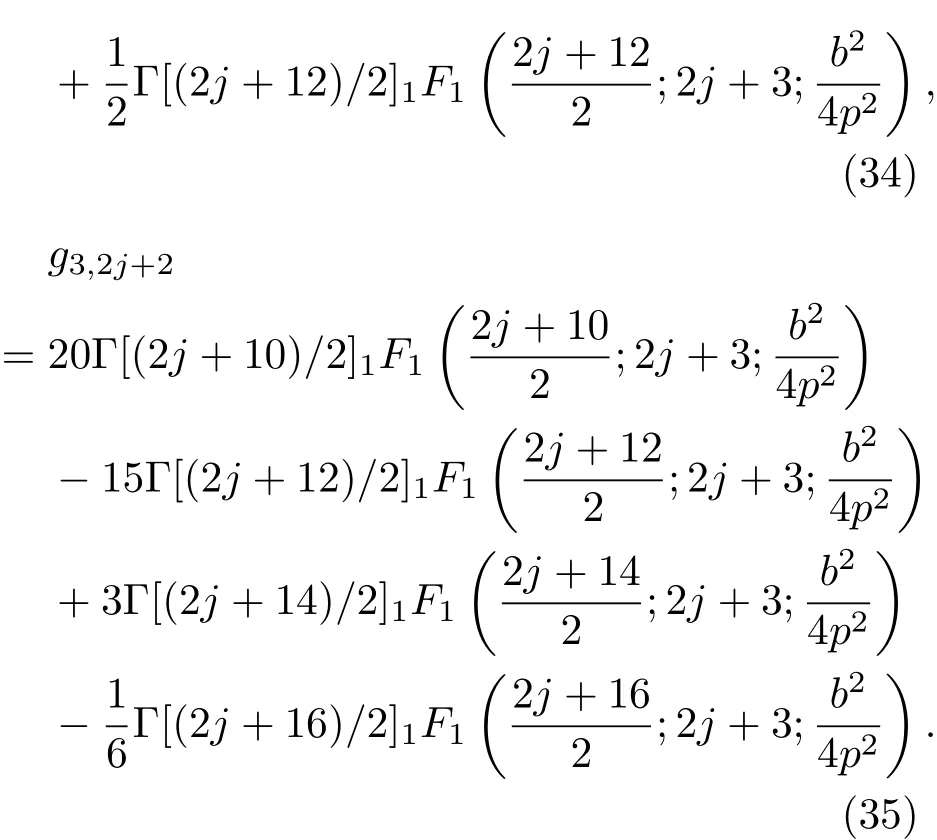
(31)式表示軸上的第一類奇型Mathieu-Gaussian光束((23)式)保留到三階非旁軸修正項(xiàng)的非旁軸表達(dá)式.典型地,取λ=632.8 nm,ω0=45μm,q=6,基于(31)式,對(duì)第一類奇型Mathieu-Gaussian光束的軸上光強(qiáng)分布進(jìn)行數(shù)值模擬,結(jié)果如圖1所示.當(dāng)傳輸距離較小時(shí),利用本文推導(dǎo)的非旁軸表達(dá)式計(jì)算得到的軸上光強(qiáng)分布結(jié)果與旁軸理論計(jì)算結(jié)果有明顯差異.很顯然,基于衍射理論研究光束近場(chǎng)傳輸時(shí),只有利用非旁軸理論才能計(jì)算得到正確的結(jié)果.但非旁軸理論的數(shù)學(xué)計(jì)算極為復(fù)雜,一般很難給出解析表達(dá)式.本文基于虛源技術(shù)的格林函數(shù)法給出Mathieu-Gaussian光束解析表達(dá)式,對(duì)于解析研究這種重要光束的傳輸有較為重要的理論價(jià)值.而且從圖1可以看出,隨著傳輸距離的增加,旁軸的近似計(jì)算結(jié)果與考慮校正項(xiàng)的非旁軸計(jì)算結(jié)果越來越接近.這說明只有在研究光束的遠(yuǎn)場(chǎng)傳輸時(shí),才能利用旁軸理論的近似法計(jì)算得到相對(duì)正確的結(jié)果.這一結(jié)論與經(jīng)典的光學(xué)理論相一致.

綜上所述,通過構(gòu)建虛源點(diǎn),利用格林函數(shù)法,本文研究了第一類奇型Mathieu-Gaussian光束,即2n+2階奇型Mathieu-Gaussian光束傳輸?shù)膰?yán)格解析表達(dá)式.另外三種Mathieu-Gaussian光束,包括第二類(2n+1階)奇型Mathieu-Gaussian光束,第一類(2n階)、第二類(2n+1階)偶型Mathieu-Gaussian光束,可作類似處理,限于篇幅,文中不再贅述.研究結(jié)果充分說明在構(gòu)建虛源點(diǎn)的基礎(chǔ)上,利用格林函數(shù)法,可很好地研究Mathieu-Gaussian光束旁軸與非旁軸光場(chǎng)分布情況,這也為研究其他復(fù)雜光束提供了很好的方法與思路.

圖1 第一類奇型Mathieu-Gaussian光束軸上光強(qiáng)分布Fig.1.The on-axis intensity distribution of the odd Mathieu-Gaussian beam of the fi rst kind.

3 結(jié) 論

根據(jù)光束傳播的獨(dú)立性和疊加性原理,Mathieu-Gaussian光束可寫為不同階次的Bessel光束無窮項(xiàng)求和的形式.這為我們借助Bessel光束的性質(zhì),在圓柱坐標(biāo)系下研究Mathieu-Gaussian光束在自由空間中的傳輸特性提供了可能.引入了一組能夠產(chǎn)生第一類(2n+2階)奇型Mathieu-Gaussian光束的虛光源點(diǎn),利用格林函數(shù)法,推導(dǎo)得到該光束在自由空間傳輸?shù)膰?yán)格解析積分表達(dá)式.根據(jù)第一類奇型Mathieu-Gaussian光束的積分形式精確解,直接計(jì)算得到光軸上光場(chǎng)分布的解析解.以三階非旁軸修正為例,得到了第一類Mathieu-Gaussian光束保留到三階非旁軸修正項(xiàng)的軸上光場(chǎng)分布精確解.研究結(jié)果充分體現(xiàn)了通過構(gòu)建虛源點(diǎn),利用格林函數(shù)法研究光束特性、非旁軸修正等光束旁軸與非旁軸光場(chǎng)分布的好處.本文基于光束傳播的獨(dú)立性和疊加性原理,利用復(fù)雜函數(shù)展開為簡(jiǎn)單函數(shù)疊加的方法,為現(xiàn)代光學(xué)中研究其他復(fù)雜光束問題提供了很好的方法與思路.

[1]Durnin J,Miceli J J Jr,Eberly J H 1987Phys.Rev.Lett.58 1499

[2]Durnin J 1987J.Opt.Soc.Am.A4 651

[3]Rajesh K B,Anbarasan P M 2008Chin.Opt.Lett.6 785

[4]Dudley A,Lavery M,Padgett M,Forbes A 2013Opt.Photonics News24 22

[5]Lorenser D,Singe C C,Curatolo A,Sampson D D 2014Opt.Lett.39 548

[6]Planchon T A,Gao L,Milkie D E,Davidson M W,Galbraith J A,Galbraith C G,Betzig E 2011Nat.Methods8 417

[7]Yan Z,Jureller J E,Sweet J,Gu ff ey M J,Pelton M,Schere N F 2012Nano Lett.12 5155

[8]Gutiérrez-Vega J C,Iturbe-Castillo M D,Chávez-Cerda S 2000Opt.Lett.25 1493

[9]Gutiérrez-Vega J C,Iturbe-Castillo M D,Ram??reza G A,Tepich??na E,Rodr??guez-Dagninob R M,Chávez-Cerdac S,Newc G H C 2001Opt.Commun.195 35

[10]Chávez-Cerda S,Padgett M J,Allison I,New G H C 2002J.Opt.B4 S52

[11]Bandres M A,Gutiérrez-Vega J C,Chávez-Cerda S 2004Opt.Lett.29 44

[12]López-MariscalC,Bandres M,Gutiérrez-Vega J,Chávez-Cerda S 2005Opt.Express13 2364

[13]Cha fi q A,Hricha Z,Belafhal A 2006Opt.Commun.265 594

[14]Gutiérrez-Vega J C,Bandres M A 2007J.Opt.Soc.Am.A24 215

[15]Alvarez-Elizondo M B,Rodríguez-Masegosa R,Gutiérrez-Vega J C 2008Opt.Express16 18770

[16]Deschamps G A 1971Electron.Lett.7 684

[17]Felsen L B 1976J.Opt.Soc.Am.A66 751

[18]Shin S Y,Felsen L B 1977J.Opt.Soc.Am.67 699

[19]Seshadri S R 2002Opt.Lett.27 1872

[20]Seshadri S R 2002Opt.Lett.27 998

[21]Deng D,Guo Q 2008Opt.Lett.33 1225

[22]Deng D,Chen C,Zhao X,Chen B,Peng X,Zheng Y 2014Opt.Lett.39 2703

[23]Gutiérrez-Vega J C,Rodr??guez-Dagnino R M 2003Am.J.Phys.71 233

[24]Li D,Wu F T,Xie X X,Sun C 2015Acta Phys.Sin.64 014201(in Chinese)[李冬,吳逢鐵,謝曉霞,孫川 2015物理學(xué)報(bào)64 014201]

[25]Li D,Wu F T,Xie X X,Wu M 2014Acta Phys.Sin.63 152401(in Chinese)[李冬,吳逢鐵,謝曉霞,吳敏 2014物理學(xué)報(bào)63 152401]

Odd version Mathieu-Gaussian beam based on Green function?

Wu Qiong1)2)?Ren Zhi-Jun1)2)Du Lin-Yue1)2)Hu Hai-Hua1)2)Gu Ying2)Yang Zhao-Feng2)

1)(Institute of Information Optics,Zhejiang Normal University,Jinhua 321004,China)
2)(Zhejiang Provincial Key Laboratory of Optical Information Detecting and Display Technology,Zhejiang Normal University,Jinhua 321004,China)

11 April 2017;revised manuscript

19 May 2017)

Like the theoretical pattern of non-di ff racting Bessel beams,ideal non-di ff racting Mathieu beams also carry in fi nite energy,but cannot be generated as a physically realizable entity.Mathieu-Gaussian beams can be experimentally generated by modulating ideal Mathieu beams with a Gaussian function,and thus they are a kind of pseudo-nondi ff racting beams with fi nite energy and fi nite transverse extent.The research of Mathieu-Gaussian beam propagating characteristics in free space is of great signi fi cance.In order to analytically study the propagation of Mathieu-Gaussian beams,the Mathieu function is expanded into the superposition of a series of Bessel functions in polar coordinates based on the superposition principle of light waves.It means that the Mathieu-Gaussian beam can be converted into accumulation of the in fi nite terms of the Bessel beams with different orders.According to the properties of the Bessel function,the free-space propagation properties of Mathieu-Gaussian beams can be studied in the circular cylindrical coordinates.Thus,a group of virtual optical sources are introduced to generate the odd Mathieu-Gaussian beams of the fi rst kind,i.e.,(2n+2)th-order,which is a family of Mathieu-Gaussian beams.Using the virtual source technique and the Green function,we derive the rigorous integral formula for the odd Mathieu-Gaussian beams of the fi rst kind.Taking for example the fi rst three orders with non-paraxial corrections,the analytical solution of the on-axis fi eld of odd Mathieu-Gaussian beams of the fi rst kind is further obtained from the integral formula.The axial intensity distribution of the odd Mathieu-Gaussian beams of the fi rst kind is numerically calculated by the integral formula.The simulation results show that the calculation results obtained with the paraxial theory and the rigorous integral expressions of nonparaxial Mathieu-Gaussian beams are obviously different when the propagation distance of the odd Mathieu-Gaussian beams of the fi rst kind is small.The calculation results of the two methods are coming closer and closer with the increasing propagation distance.The results indicate that the correct results can be obtained with the paraxial theory when we study the propagation of Mathieu-Gaussian beams in the far- fi eld,but the non-paraxial theory must be used to obtain correct results when we study the propagation of Mathieu-Gaussian beams in the near- fi eld.Owing to the complexity of the non-paraxial theory,it is difficult to obtain the exact analytic solutions of Mathieu-Gaussian beams in the near- fi eld with the classical di ff raction theory.Based on the superposition principle of light waves,by introducing the virtual source technique and the Green function,the complex Mathieu-Gaussian function can be expanded into the superposition of a series of simple Bessel functions,and the axial intensity distributions of Mathieu-Gaussian beams in the far- fi eld and the near- fi eld can be studied well.It will also provide a feasible method to study other complex beams propagating in free space.

Green function,Mathieu-Gaussian beams,virtual sources

(2017年4月11日收到;2017年5月19日收到修改稿)

10.7498/aps.66.204201

?國家自然科學(xué)基金(批準(zhǔn)號(hào):11674288)和浙江省教育廳科研項(xiàng)目(批準(zhǔn)號(hào):Y201534211)資助的課題.

?通信作者.E-mail:wuqiong@zjnu.cn

?2017中國物理學(xué)會(huì)Chinese Physical Society

http://wulixb.iphy.ac.cn

PACS:42.25.Bs,42.68.Ay,42.30.KqDOI:10.7498/aps.66.204201

*Project supported by the National Natural Science Foundation of China(Grant No.11674288)and the Education Department Program of Zhejiang Province,China(Grant No.Y201534211).

?Corresponding author.E-mail:wuqiong@zjnu.cn