基于二分遞推奇異值分解的故障測距研究

段啟凡，楊 桐

?

基于二分遞推奇異值分解的故障測距研究

段啟凡，楊 桐

提出利用二分遞推奇異值分解與改進的D型測距算法相結合的故障測距算法，該算法能有效消除諧波的干擾和減弱負荷變化對測距結果的影響。仿真結果表明，基于二者相結合的故障測距方法可以準確計算故障點位置。

故障測距；二分遞推SVD；D型測距算法

0 引言

隨著電氣化鐵路運營里程和速度的不斷提高，電氣化鐵路安全運營成為一項重要課題。AT供電方式可將列車和變電所之間的電壓提高1倍，在同樣牽引功率下網上電流減小，電壓損失和功率損失相應減少[1]，因而在我國高速鐵路中得到了廣泛應用。由于該方式的線路結構復雜，故障排查相對困難，因而研究AT供電方式的故障測距方法，對于故障的查找和排除具有重要意義[2]。

由數學分析可知，故障電壓行波中的奇異點坐標對應初始行波到達檢測點的時間，進而可以得到故障距離。行波法中的小波變換模極大值可以表征信號的奇異點，故行波法成為故障測距的重要算法[3]。從理論出發，需要針對不同故障狀態選擇合適的Daubechies小波族的某個特定小波作為分析工具，且小波一旦確定下來，其可檢測的奇異性指數也因此固定[4]。但是在實際操作過程中，專家學者僅憑經驗選擇某個特定小波，則無法避免故障測距產生的誤差。SVD奇異值分解理論在奇異點提取和故障診斷領域得到廣泛研究[5，6]。文獻[7]將SVD和小波變換相結合對機電信號進行正交變換，提取代表運動的最優特征完成對指定對象的控制。文獻[8]通過SVD對隱形空間中模式進行線性獨立性分析，計算神經元個數。文獻[9]利用小波各尺度結果的平方值形成一個能量分布矩陣，通過識別奇異值分解后的第一個奇異值所對應的分量，可以實現對振動系統頻率的識別。

行波法中最常用的A型和D型算法的測距精度會受到運營線路長度和實際波速的影響[10]。為減小波速和線路長度對故障測距結果的影響，專家學者做了相應研究。文獻[11]利用2種模量的時間延遲區分故障點反射波與對端母線反射波，但該方法易受到地上分量速度變化的影響；文獻[12]利用故障點和對端母線反射波極性的不同，區分二者到達檢測端的時間，但在一定條件下，母線反射波的極性會發生變化，導致無法準確識別故障點反射波。

本文將奇異值分解與D型測距算法相結合研究AT供電方式的故障測距方法。首先對鋼軌與保護線進行等效處理，得到牽引網阻抗計算式，以此搭建等效模型；然后對模型進行仿真，得到行波信號；將其進行凱倫貝爾變換后完成二分遞推SVD，利用各分量的振蕩位置確定故障初始行波和故障點反射波分別到達檢測端的時間；再代入改進的D型算法中，準確計算出故障發生的位置。仿真實驗表明，本文提出的將二分遞推奇異值與改進的D型測距算法相結合的故障測距方法具有良好的實用性和準確性。

1 AT供電方式的線路阻抗推導

AT供電方式中，保護線是為降低鋼軌電位、提供故障電流通路而專門鋪設的[13]。由于鋼軌與保護線相連，二者具有相同的外電壓，因此在計算阻抗時可以將二者等效成一條導線，減少了未知量的個數，為之后的電路建模提供方便。依據Carson理論可知[13]，任何導線-地的單位自阻抗為

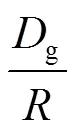
導線-地回路間的單位互阻抗為

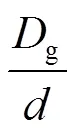
式中，為單位長自電阻；g為等效大地回線的入地深度；為導線的等效半徑；為平行導線的中心距離（由幾何均距法算出）。

根據帶保護線AT供電系統的實際情況，參照式（1）、式（2），可以推導出接觸線與等效導線的互阻抗為

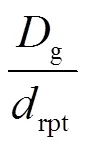
式中，rpt為接觸線與等效導線的中心距離。

接觸線、鋼軌的互阻抗和接觸線、保護線的互阻抗分別為

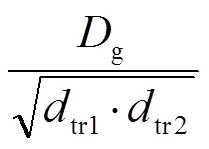
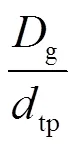
式中，tr1、tr2、tp分別為接觸線與平行的鋼軌1、鋼軌2、保護線的中心距離。

最終可得到等效導線與接觸線的互阻抗為

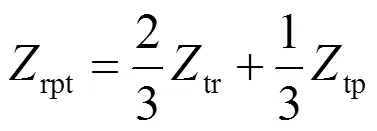
同理，等效導線與正饋線的互阻抗為

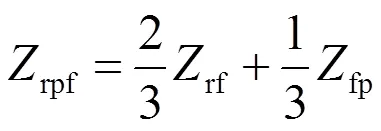
式中，rf為鋼軌和正饋線互阻抗，fp為正饋線和保護線互阻抗。

接觸線、等效導線和正饋線的自阻抗分別為

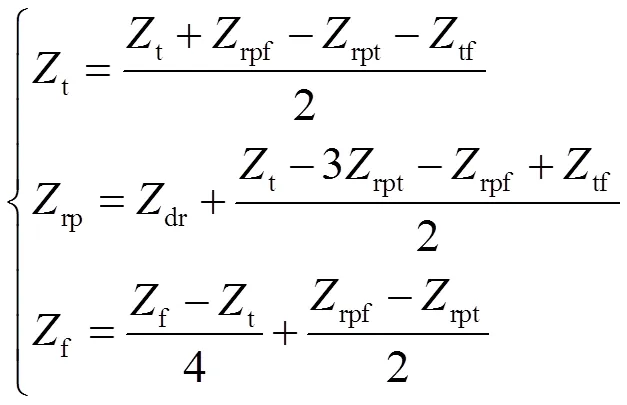
式中，tf為接觸線和正饋線互阻抗，dr、f、t分別為鋼軌、正饋線和接觸線自阻抗。

根據牽引網線路阻抗的推導，以實際牽引網為例[11]，得出線路阻抗的模型如圖1所示。

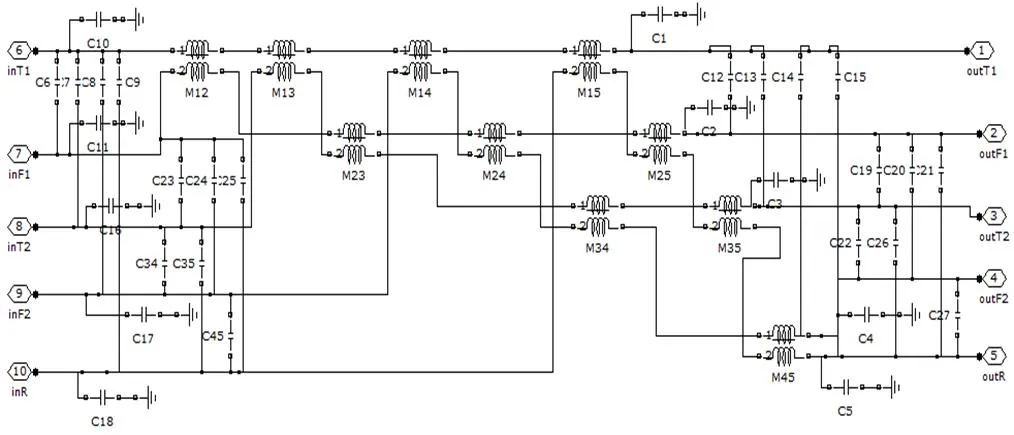
圖1 線路阻抗模型

在考慮自阻抗和互阻抗情況下，求得5×5線路阻抗矩陣，見式（9）。該矩陣的對角線元素分別為上行接觸線、上行正饋線、下行接觸線、下行正饋線和鋼軌保護線的自阻抗；其他位置元素均為互阻抗，第1行和第1列元素分別代表上行接觸線、上行正饋線、下行接觸線、下行正饋線和等效線路。

電容系數矩陣為

2 二分遞推SVD原理的故障測距與應用

2.1 二分遞推SVD分解原理

SVD是指：實矩陣∈m×n存在正交矩陣= [1,2,…m]∈m×n和= [1,2,…n]∈n×m，令

=T（11）

成立[14]。其中矩陣= [diag(1,1,…q),]的元素是矩陣中所有的奇異值，其中為零矩陣，= min[,]。正交矩陣和分別為矩陣的左、右奇異向量，也分別是矢量空間的標準正交基底。

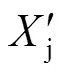
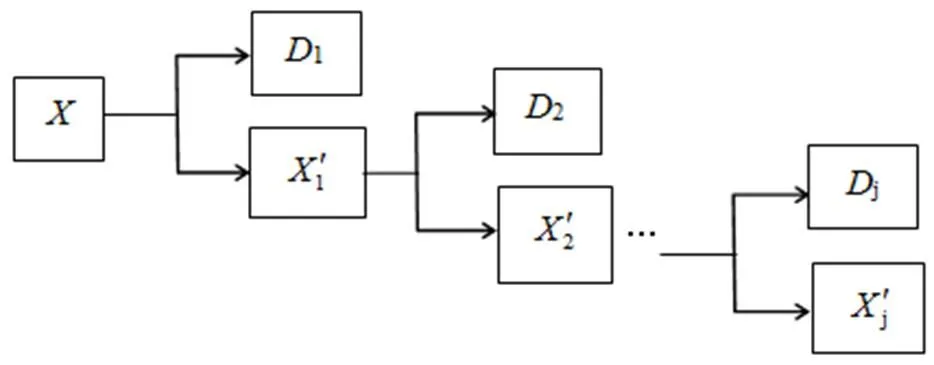
圖2 二分遞推SVD分解過程

這種利用行波信號的迭代過程實現信號的逐次剝離、逐次分析，與小波多分辨率分解相似。該方法得到的分解結果位于不同層次的矢量空間中，且下一層空間的基矢量是根據上一層的近似基矢量獲得，實現了對信號逐次剝離的多層次分解。整個分解過程不會產生2個以上的信息分量，計算量較小，計算速度較快。

2.2 二分遞推SVD在故障測距數據處理中的應用

采用二分遞推SVD算法，可以通過各分量檢測出不同奇異性指數的奇異點，而小波變換算法在小波基確定后就不具備該功能[15]。

由二分遞推SVD分解算法可以計算得到故障行波的多層分量信號，由振蕩位置的坐標換算出行波和反射波到達檢測端的時間，其基本步驟如下：

（1）通過仿真，獲得一維故障行波信號= [(1),(2),…()]，凱倫貝爾變換解耦線路中的電磁耦合關系，得到0模、模和模分量[16]。利用穩定的模分量構造一個行數為2的Hankel矩陣：

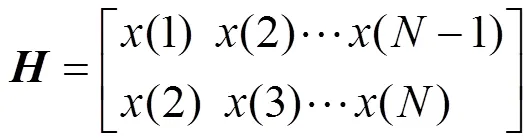
式中，∈2×(N-1)。

將式（12）通過二分遞推SVD后可以轉化為2個列向量的表示形式，即

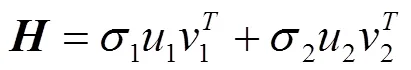
式中，u∈2×1；v∈(N-1)×1，= 1,2。

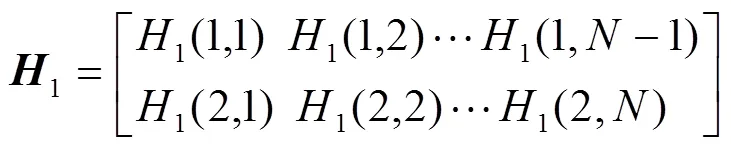
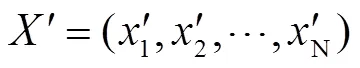
（3）對進行了第次分解的矩陣的首行和除去第一行元素的最后一列構造向量。

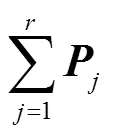
由式（15）可知，故障信號被剝離成一系列分量信號[18]。在今后的故障分析中，要研究某個特定分量就相當于在行波信號中用減法進行簡單提取，這種減法運算可以保證提取的分量在行波信號中的相位不會發生變化[19]。

（4）利用分量中的振蕩信息對故障行波和反射波到達檢測端的時間進行準確的提取。

3 D型測距算法的改進與綜合應用

3.1 D型測距算法

D型測距算法需要波速和行波波頭到達檢測點的時間，求解后者必不可少的已知條件是待測線路的實際長度。很多學者為了簡化計算將波速設定為光速，將線路實際長度設為水平檔距[20]，這些假設都會影響實際故障測距的精度。

波速大小取決于土壤電阻率的分布情況和架空線路參數。由于溫度影響，線路的不均勻電暈分布會發生變化進而影響分布電容和分布電感的大小，最終導致傳播速度的變化。輸電線路的實際線長與環境溫度和線路負荷狀態有關。文獻[21]以一條100 km的線路為例，在綜合因素作用下線長的誤差可以達到1 km。所以有必要對現有的D型測距法進行改進，推導出一種不受波速和線路長度影響的測距算法。

3.2 改進的D型測距算法

D型測距原理是利用線路產生的初始行波波頭到達線路檢測點的時間之差來計算故障點距離。如圖3所示，初始行波波頭在故障兩側線路傳播所用時間分別為1和2，由圖3可以得到故障距離為[22]

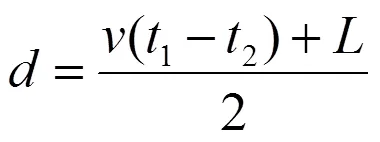
式中，為行波傳播速度，為線路全長。

圖3 行波折反射示意圖

針對現有D型測距算法中的缺陷對其進行改進，得到一種避免波速和線路長度變化對故障測距結果產生干擾的改進算法。

D型測距算法的行波折反射模型如圖3所示，設線路總長為，波阻抗為0，過渡電阻為f，行波的傳播速度為，故障發生點與測量點右側距離為圖中1、3和2、4分別是故障行波從點第一次和第二次到達點和點所用的時間。在發生遠端故障時，對端線路的反射波在點發生折射會先于反射波到達本端，通過凱倫貝爾變換可以判斷第二個波的來源與極性[23]。

假設1＜2，即點靠近側，此時3是故障點反射波到達側所用時間，4為故障點折射波到達側所用時間。根據圖3建立方程組：

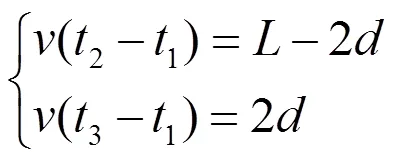
解方程組得到

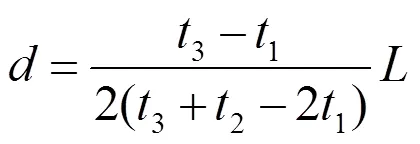
當1＞2時，即點靠近側，此時3是故障點折射波到達側所用時間，4為故障點反射波到達側所用時間。根據圖3再建立方程組：

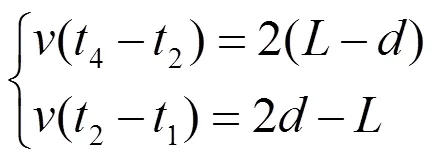
解方程組得到

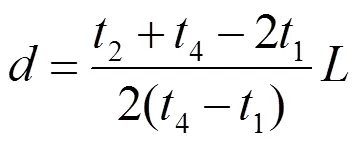
由式（18）和式（20）可知，改進算法只需要初始行波和反射波到達兩側所用時間和線路總長，就可計算出故障距離；和同時出現在等式兩側，消除了線路下垂或環境因素導致的實際長度不等于水平檔距時對故障測距精度的影響。而且式（18）和式（20）中不涉及行波傳播速度的計算，消除了波速變化對故障測距精度的影響。為進一步消除諧波的干擾和減弱負荷變化對故障測距結果的影響，依據工頻周期的采樣點數，采用在點左右兩側選取電流行波的差值進行計算，即

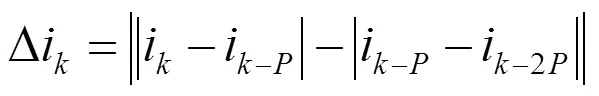
采樣的電流數據誤差在第一次相減時已經產生，2個采樣誤差再進行一次相減即可以將整體數據誤差抵消。這種改進的D型測距算法具有更高的精確度。

3.3 2種測距算法的綜合應用

二分遞推SVD與改進D型測距算法的綜合流程如圖4所示。首先將原始數據進行凱倫貝爾變換，將變換得到的模分量放入矩陣中，參照第2.2節中的數據處理過程，通過矩陣中振蕩信息的位置確定折反射波到達檢測端的時間，判斷第二個到達的行波和原始行波極性，以此代入相應的改進D型測距算法的計算式中，求出故障點位置。

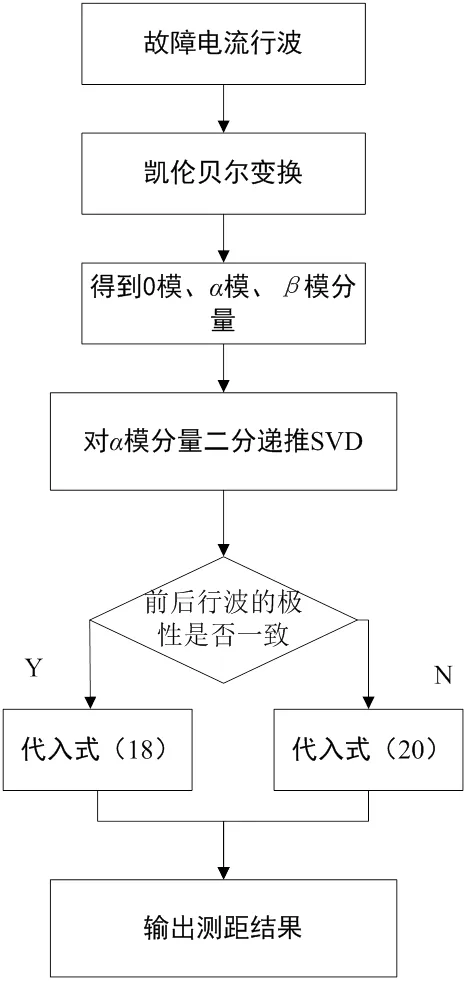
圖4 綜合流程

4 仿真實驗

基于圖1所示的線路阻抗圖，可以得到AT供電牽引網的仿真模型，如圖5所示。用Matlab進行故障仿真，主要參數：系統電源220 kV；系統阻抗0.5+j4.71 Ω；AT1與VX-T段和AT1與AT2距離各為20 km；牽引變壓器容量為8.5 MV·A[24]。

設在距離故障端點15 km處發生接觸線-鋼軌的接地短路故障，過渡電阻為10W，采樣頻率為1 MHz。將故障電流行波通過第2.2節的數據處理過程得到圖6。

圖5 仿真系統模型

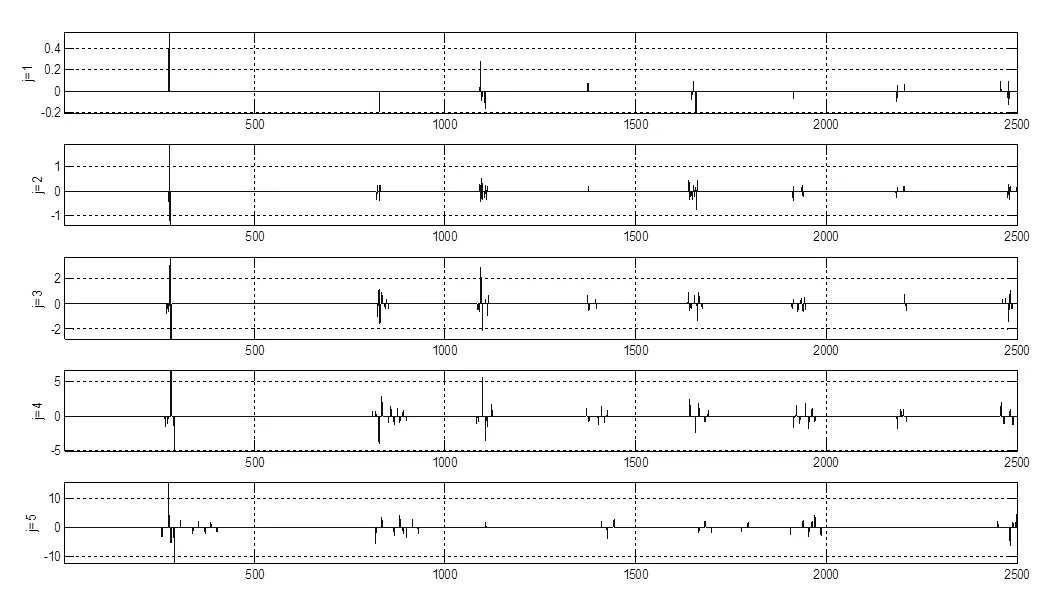
圖6 二分遞推SVD分解的分量信號波形

由圖6可以看出，各個分量中產生了若干振蕩波形，這些振蕩波形在每個子圖中都有體現。顯然，對應這些振蕩的不是白噪聲，因為白噪聲不會如此有規律地出現在各個分量的對應位置，因而這些振蕩波形的中心點反映的是故障行波中若干奇異點的位置[25]。

為了檢驗二分遞推SVD在查找奇異點方面的性能，本文選用以往文獻常用的對稱三次B樣條小波進行小波變換，選取第2層小波細節分量進行奇異點的查找，對比結果如表1所示。

從表1可以看出，故障點設置在35 km處及以后，常用的三次B樣條小波發揮了緊支撐、對稱和線性相移的優勢，識別奇異點的可靠性高于二分遞推SVD；但是采用二分遞推SVD在判斷故障距離時只與實際故障位置相差約0.02 km，最大相差0.68 km，采用小波變換故障測距產生的誤差一般都大于采用二分遞推SVD時的故障測距誤差。

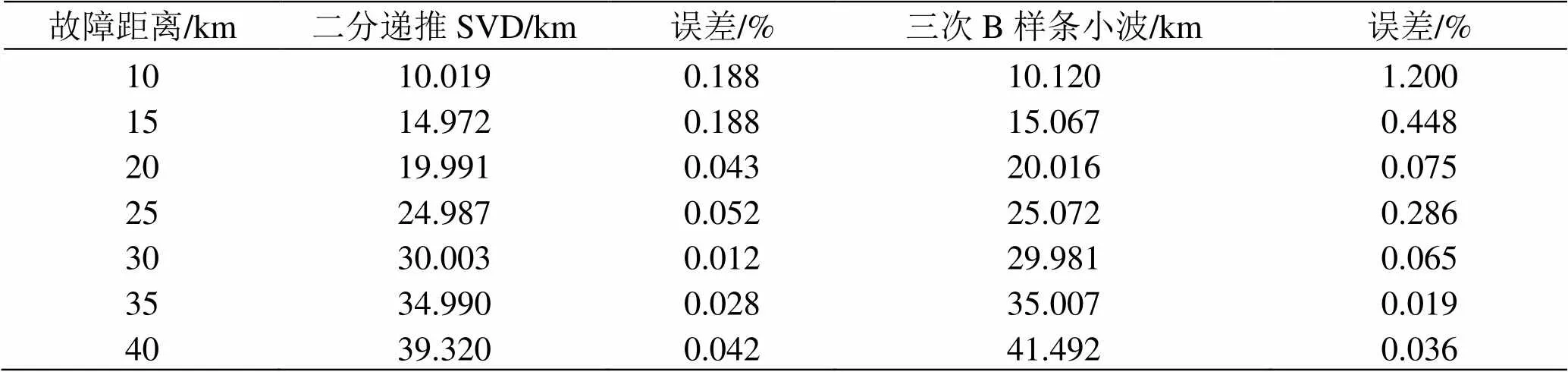
表1 二分遞推SVD與小波變換對比

當線路實際長度發生變化或波速設定為光速時，將改進的D型算法與一般D型算法進行對比，對比結果見表2。

由于工程上通常根據不同輸電線路的電壓等級選擇一個接近光速的近似值來表示波速，波速的取值范圍一般在0.936（110 kV）～0.987（500 kV），所以本文選取波速誤差為-1%和-2%進行對比。同理線路長度的誤差依據工程經驗設定為1%和-1%。

在實際仿真過程中，以線路長度誤差1%為例，設定波速為光速，分別對比2種算法求解出的故障距離誤差。同理，設置波速誤差后，規定線路長度即為水平檔距，對比2種算法的故障距離誤差。

由表2可知，線路實際長度和波速的變化對改進算法的計算誤差沒有太大影響，但對于一般D型算法，這2個參數的微小變化對最后的故障測距誤差產生了很大影響。所以，在相同條件下，改進的D型算法比一般D型算法具有更高的精度。

表2 波速與線路長度對故障測距誤差的影響分析 km

針對AT供電方式下的故障測距，“AT中性點吸上電流比”、“橫聯線電流比”等方法基本適合工程需要，但測距結果會受到過渡電阻的影響。

本文基于設置不同的過渡電阻和故障距離，應用二分遞推SVD與改進D型算法相結合的綜合算法，得到如表3所示的故障測距仿真結果。可以看出，在不同過渡電阻和故障距離的情況下，改進的D型測距算法與二分遞推SVD相結合的方法使仿真結果具有很高的精度。在同一故障距離處，經過不同的過渡電阻，計算結果完全一致，說明本文提出的這種二分遞推SVD與改進的D型測距算法相結合的故障測距方法不受過渡電阻的影響。

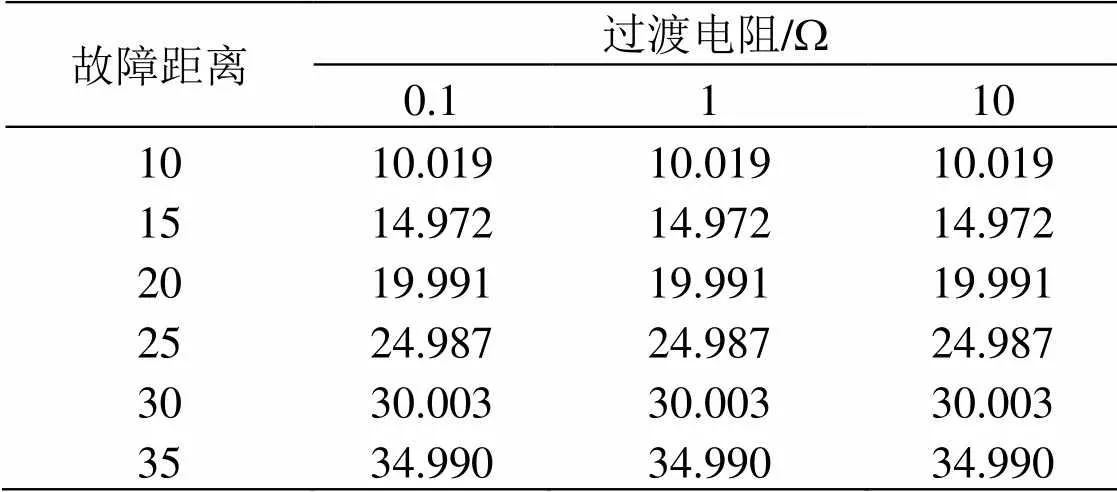
表3 綜合算法的仿真測距結果 km

5 結論

（1）本文通過凱倫貝爾變換將故障電流行波信號轉化為3個分量信號，選取其中的模分量構造Hankel矩陣，利用二分遞推SVD找到信號的奇異點。在尋找奇異點過程中，與小波變換相似，振蕩波形的中心點對應奇異點的位置。

（2）提出一種不受波速和線路長度影響的改進D型測距算法，利用行波突變量消除負荷變化對故障測距結果的影響；通過時間之比和線路長度的乘積準確找到故障點位置。與一般D型測距算法相比，改進算法消除了波速誤差造成的測距誤差，且不受線路長度變化的干擾，具有更高的精度。

（3）將二分遞推SVD與改進的D型測距算法相結合的綜合故障測距算法不受過渡電阻的影響，具有較強的抗干擾性。

[1] 魏立新，張俊林，劉青松. 基于改進人工魚群算法的神經網絡優化[J]. 控制工程，2014，21.

[2] 張殿瑞. 接觸網短路暫態仿真與行波測距裝置開發[D].北京：北京交通大學，2009.

[3] Grispino A S,Petracca G O,Dominguez A E.Comparative analysis of wavelet and EMD in the filtering of radar signal affected by brown noise[J]. Latin America Transcations,IEEE, 2013,11(1):81-85.

[4] 李國勇，閆芳，郭曉峰. 基于遺傳算法的灰色神經網絡優化算法[J]. 控制工程，2013，20（5）：934-937.

[5] 向強銘. 基于奇異值分解理論的輸電線路雷擊故障測距的研究[D]. 成都：西南交通大學，2014.

[6] Figarella T, Jansen M H.Brush wear detection by continuous wavelet transform[J]. Mechanical Systems and Signal Processing, 2007,21(3):1212-1222.

[7] XIE Hongbo, ZHENG Yongping, GUO Jingyi. Classification of the mechanomyogram signal using a wavelet packet transform and singular value decomposition for multifunction prosthesis control[J]. Physiological Measurement, 2009,30(5):441-457.

[8] 唐炬，李偉，歐陽有鵬. 采用小波變換奇異值分解方法的局部放電模式識別[J]. 高電壓技術，2010，36（7）：1686-1691.

[9] Brenner M J. Non-stationary dynamic data analysis with wavelet-SVD filtering[J]. Mechanical System and Signal Processing, 2003,17(4):765-786.

[10] LI Chun-feng,Liner C.Wavelet-based detection of singularities in acoustic impedances from surface seismic reflection data[J].Geophysics,2008,73(1):1-9.

[11] LI Rui-feng,ZENG Xiang-jun,LIU Hui,et al.The application of precision clock synchronization technology based on PTP in traveling wave fault location system[C]//The International Conference on Advanced Power System Automation and Protection,2011,5:1631-1635.

[12] GALE P. F.,TALOR P. V.,HITCHIN C.,et al.Traveling wave fault locator experience on Eskom’s transmission network[A].Developments in power system protection, 2001, Seventh International Conference on(IEE)[C]. Amsterdam Netherlands:IEE,2001.327-330.

[13] Abur A.,Mangnago F. H..Use of delays time between model components in wavelet based fault location[J].Electrical Power and Energy Systems,2000,22(6):397-403.

[14] 黃子俊，陳允平. 基于小波變換模極大值的輸電線路單端故障定位[J]. 電力自動化設備，2005，25（2）：10-13.

[15] AKRITAS A. G.,MALASCHONOK G. I.Applications of sigular value decomposition[J].Mathematics and Computers in Simulation,2004,67(1):15-31.

[16] SHIN K.,FERADAY S. A.,HARRIS C. J.,et al.Optimal autoregressive modelling of a measured noisy deterministic signal using sigular value decomposition[J].Mechanical Systems and Signal Processing,2003,17(2):423-432.

[17] WALTON J.,FAIRLEY N..Noise reduction in X-ray photoelectron spectromicroscopy by a singular value decomposition sorting procedure[J].Journal of Electron Spectroscopy and Related Phenomena,2005,148(1):29-40.

[18] VANLANDUIT S.,CAUBERGHE B.,GUILLAUME P..Reduction of large frequence response function data sets using robust singular value decomposition[J].Computers and Structures,2006,84(12):808-822.

[19] 宋乾坤，柳斌. 矩陣奇異值的兩個不等式的推廣[J]. 自貢師專學報，1994，（4）：77-79.

[20] 趙學智，葉邦彥. SVD和小波變換的信號處理效果相似性及其機理分析[J]. 電子學報，2008，8（8）：1582-1583.

[21] Hanninen E. M..Charateristics of earth faults in electrical distribution networks with high impedance earthing[J].Electric Power System Research,1998(44):122-161.

[22] 賈俊國，范云鵬，李京. 利用電流行波的輸電線路故障測距技術及應用[J]. 電網技術，1998，22（8）：64-65.

[23] 馬丹丹，王曉茹. 基于小波模極大值的單端行波故障測距[J]. 電力系統保護與控制，2009，37（3）：55-59.

[24] 劉亞東.動態提高輸電線路容量系統硬件平臺的設計與實現[D]. 上海：上海交通大學，2007.

[25] 趙學智，葉邦彥，陳統堅. 奇異值差分譜理論及其在車床主軸箱故障診斷中的應用[J]. 機械工程學報，2010，46（1）：100-108.

The fault location algorithm combined with D type ranging algorithm and dichotomizing recursion singular value decomposition is proposed. The algorithm is able to eliminate effectively the harmonic interference and side effects to the distance measurement due to variations of loads. The simulation results show that the fault location method is able to calculate the faulty point accurately.

Fault location; dichotomizing recursion singular value decomposition (SVD); D-type ranging algorithm

10.19587/j.cnki.1007-936x.2017.05.010

U226.5

A

1007-936X(2017)05-0039-07

段啟凡.中國鐵路設計集團有限公司，助理工程師；楊 桐.國網青海省電力公司經濟技術研究院，工程師。

2016-12-09