考慮附加強化效應的多軸穩態循環塑性本構模型

李 靜， 李春旺， 張忠平

(空軍工程大學 理學院， 西安 710051)

考慮附加強化效應的多軸穩態循環塑性本構模型

李 靜， 李春旺， 張忠平

(空軍工程大學 理學院， 西安 710051)

已有試驗結果表明，非比例循環加載下應變主軸連續旋轉，導致多滑移系開動，阻礙材料內部形成穩定的位錯結構，使非比例加載下的應力-應變曲線高于比例加載下的應力-應變曲線，從而產生非比例附加強化現象. 由此，從應力空間表述的塑性增量本構模型一般形式出發，建立一個能夠反映非比例附加強化效應的穩態循環塑性本構模型. 在Armstrong-Frederick模型背應力演化方程的基礎上，新模型通過引入非比例度因子和附加強化系數，構建了一個新的背應力演化方程. 然后，通過一致性條件建立塑性模量方程與背應力之間的關系. 同時，利用最小法向應變范圍，提出一種計算非比例度因子的新方法，并針對一般的多軸加載情形，明確最小法向應變范圍的計算步驟. 新模型從加載路徑和材料本身兩個方面來考慮非比例附加強化效應的影響，克服Armstrong-Frederick模型中材料常數確定方法繁瑣，且通過單軸疲勞試驗數據確定的材料常數不能很好地反映材料非比例附加強化現象的不足. 應用新模型時，僅僅需要3個獨立的常規力學參量和2個疲勞參數，便于工程應用. 利用多種多軸加載路徑下S460N鋼和304不銹鋼的試驗結果對模型進行驗證，預測結果與試驗結果吻合良好.

非比例附加強化；穩態循環應力應變響應；塑性本構模型；非比例度因子；附加強化系數

多軸循環應力-應變關系是指材料在多軸載荷下應力-應變響應的變化關系. 目前主要有兩種方法來描述這種變化關系[1]：一種是經驗公式法，另一種是循環本構模型. 經驗公式法是基于全量理論來描述多軸循環應力-應變關系. 這種方法簡單、實用、方便. 但是，經驗公式法僅僅能較好地描述幾種典型多軸加載下的應力-應變關系. 因此，各國研究者更多的是基于增量理論，利用循環本構模型來描述材料的應力-應變關系.

20世紀60年代以來，人們提出了眾多基于增量理論的循環本構模型，但不論何種模型，大都由三個基本部分組成[2]：屈服準則；流動規律；硬化規律. 對于屈服準則和流動規律，各模型基本都相同. 而硬化規律隨著加載方式的逐漸復雜，被不斷修正，從最初的線性硬化規律逐漸發展到非線性硬化規律. Armstrong等[3](A-F模型)在隨動強化律的基礎上，通過引入一個動態恢復項使隨動強化率具有非線性特征，建立了著名的動力恢復模型. Chaboche等[4]提出非線性硬化規律可以用一系列的背應力分量來表示，對A-F模型進行修正. 楊顯杰等[5]定義材料的屈服面和極限面分別遵循不同的演化規律，通過引入加載路徑的非比例度，提出一個可考慮材料循環強化/軟化效應、塑性應變歷史效應和非比例循環加載效應的雙曲面模型. D?ring等[6]分析發現Jiang模型[7]不能很好的反映材料的非比例附加強化現象，通過引入Tanaka非比例度因子[8]，對Jiang模型進行修正. Khutia等[9]也通過引入Tanaka非比例度因子[8]對Chen等修正的Ohno-Wang模型[10]進行了進一步修正，并利用304不銹鋼的試驗結果對修正模型進行驗證. Meggiolaro等[11]對Tanaka非比例度因子進行瞬態響應修正，并引入到Jiang模型中，較好地描述了316L不銹鋼的非比例附加強化現象. Gates等[12]基于Tanaka非比例度因子提出一個新的瞬態硬化準則，并利用該準則對Zhang-Jinag模型[13]進行修正，修正模型較好地描述多種復雜載荷路徑下2024-T3鋁合金的非比例附加強化現象. Wu等[14]利用Tanaka非比例度因子[8]，在退化的2維偏應力-應變空間中量化了塑性應變對廣義塑性模量的影響，所建多軸本構關系可以體現三種強化效應. Shamsaei等[15]利用304L不銹鋼和1050QT合金鋼系統研究了多種復雜非比例加載路徑下材料的附加強化效應，通過驗證發現Tanaka非比例度因子[10]可較好地反映材料的非比例附加強化現象. 雖然Tanaka非比例度因子應用較為廣泛，但是該因子中的材料常數需要借助相關多軸疲勞試驗予以確定[16].

Itoh等[17]引入一個新的非比例度因子，建立一個新的循環本構模型，該模型可以描述材料的非比例附加強化現象，且只含有6個材料常數，便于計算. 但是，利用多種復雜多軸加載下6061-T6鋁合金的試驗結果對模型進行驗證發現，模型中的附加強化系數對模型的計算精度影響較大，而合理地確定附加強化系數，就需要借助材料的多軸疲勞試驗數據，給模型的進一步應用帶來不便. Kowalewski等[18]建立一個三曲面本構模型，并利用新模型較好地描述了2024鋁合金的單/多軸應力-應變響應. 但是，該模型的材料常數較多且大多需要借助試驗予以確定，而Kowalewski等[18]未給出這些材料常數的具體確定方法. Madrigal等[19]通過定義應力空間相鄰加載點的距離方程，建立一個新的多軸本構模型. 但是，該距離方程也需要借助多軸疲勞試驗予以確定. 概括來講，對于建立在A-F模型[3]基礎上，塑性模量通過一致性條件得到的耦合類本構模型，至少存在以下三方面的問題：模型中材料參數較多，計算繁瑣；需要較多的附加單軸及多軸疲勞試驗來確定模型中的材料常數；模型過于復雜，不利于工程應用.

為克服現有本構模型的上述缺點，本文在A-F模型背應力演化方程的基礎上，通過引入非比例度因子和附加強化系數，構建一個新的背應力演化方程. 然后，通過一致性條件建立塑性模量方程與背應力之間的關系. 同時，利用最小法向應變范圍，提出一種計算非比例度因子的新方法. 利用多種多軸加載路徑下S460N鋼和304L不銹鋼的試驗結果對模型進行了驗證，預測結果與試驗結果吻合良好.

1 多軸循環本構模型的描述

一個完整的循環塑性本構模型一般由屈服準則、流動規律和硬化規律三部分組成. 在彈性范圍內，應力可利用Hooke定律由應變確定，但在循環塑性變形過程中，應力-應變取決于加載歷史，應力-應變通常利用增量理論來確定.

1.1屈服準則

對于復雜應力狀態，材料是否進入塑性狀態，一方面和這些應力分量有關，另一方面與材料的力學性能有關. 就大多數金屬材料而言，恒溫下受到循環加載時，應當主要考慮加載歷史對應力-應變響應的影響. 本文定義屈服條件服從von-Mises屈服準則

Fi(s,α,k)=(s-α):(s-α)-2k2.

(1)

式中:s為偏應力張量，α為背應力張量，k為單剪狀態下的屈服強度，張量之間的“：”表示張量的點積.

1.2流動規律

根據小變形理論，總應變增量dεt由彈性應變增量dεe和塑性應變增量dεp兩部分組成

dεt=dεe+dεp.

(2)

式中彈性應變增量dεe可由Hooke定律求得

(3)

式中：E為彈性模量，νe為彈性泊松比，dσ為應力增量張量，I為二階單位張量. 塑性應變增量dεp可由流動規律求得[2, 7]：

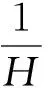
(4)

其中:

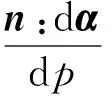
(5)

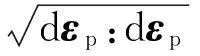
(6)

(7)

(8)

式中：“〈〉”為MacCauley括號，“‖‖”為張量函數的模，de為偏彈性應變增量，G為剪切模量.

由式(4)可知，當ds:n>0時，材料產生塑性變形. 由式(4)～(8)，可得

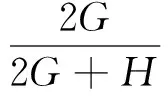
(9)

對于控制應力加載，塑性應變增量可用式(4)進行計算. 對于控制應變加載，與式(4)相比，塑性應變增量利用式(9)進行計算更為方便.

1.3硬化規律

Jiang等[20]將A-F模型中的背應力演化方程重新表述為

(10)

式中c和r都是材料常數.

在A-F模型中，材料常數c和r的確定方法繁瑣，而且在非比例加載下，利用單軸疲勞試驗數據確定的材料常數并不能很好地反映材料的附加強化現象. 為此，本文引入附加強化系數和非比例度因子對A-F模型的背應力演化方程進行進一步修正.

Socie等[2]指出，多軸加載下，材料的應力-應變關系可用Ramberg-Osgood公式為

σeq=(1+αnpfnp)K′(εeq,p)n′.

(11)

此時，材料的塑性模量為

(12)

式中：σeq為von-Mises等效應力，εeq,p為von-Mises等效塑性應變，K′為循環強度系數，n′為循環應變硬化指數，fnp為非比例度因子. 附加強化系數αnp定義為[1]

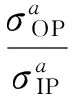
(13)

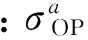
將式(10)代入式(5)，可得

(14)

由式(14)中求出cr后代入式(10)，可得

p.

(15)

將式(12)代入式(15)，可得背應力演化方程為

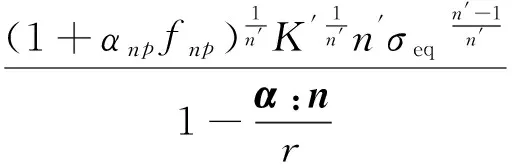
(16)

試驗驗證發現，當r取值遠大于材料的屈服面半徑時，r取值對材料應力-應變響應的計算結果影響不大. 因此，本文中將材料常數r取為K′.

根據一致性條件可知，單軸循環加載下，式(16)確定的塑性模量方程退化為由Ramberg-Osgood曲線確定的單軸塑性模量方程.

1.4非比例度因子

用K′代替式(16)中的材料常數r后，除了K′和n′，式(16)中不含有額外的材料常數. 但是，在計算過程中，需要確定不同加載路徑下的非比例度因子fnp，以反映加載路徑非比例程度對材料循環應力-應變的影響. 因此，進一步建立fnp的計算公式.

拉扭加載下，與薄壁圓管試件軸向夾角為α的平面上的法向應變εn,α和剪切應變γα分別為[21]：

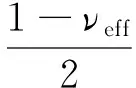
(17)

γα=-(1+νeff)εxsin 2α+γxycos 2α.

(18)

式中νeff為等效泊松比，可將其取為0.5[2].

以正弦波加載為例，在控制應變下對薄壁圓管試件施加的軸向應變εx和剪切應變γxy為：

(19)

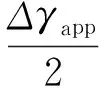
(20)

式中:Δεapp和Δγapp分別為施加的軸向和剪切應變范圍，φ為載荷間的相位差.

由式(17)～(20)可得，與薄壁圓管試件軸向夾角為α的平面上的法向應變范圍Δεn,α和剪切應變范圍Δγα分別為[21]：

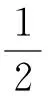
νeff)cos2α-2νeff+λsin 2αcosφ]2}0.5,

(21)

Δγα=Δεapp{[λcos 2αsinφ]2+[λcos 2αcosφ-(1+νeff)sin 2α]2}0.5.

(22)

式中λ(=Δγapp/Δεapp)為應變比.

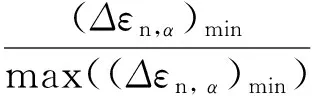
(23)

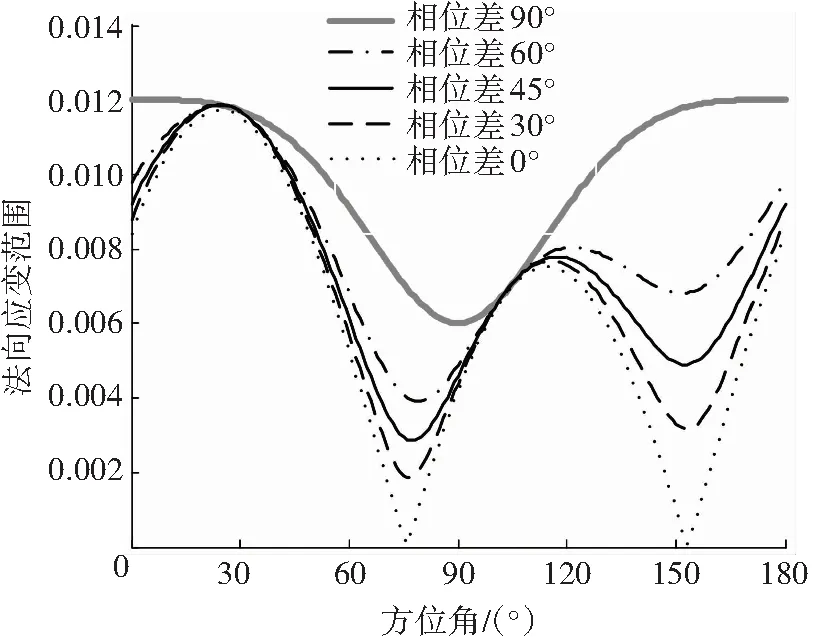
圖1 不同相位差下各平面的法向應變范圍(正弦波)

Fig.1 The normal strain range,Δεn,α, of each plane under different phase delays (sinusoidal wave)

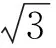
當加載波形為正弦波且軸向應變εx和剪切應變γxy的加載頻率相同時，可直接利用式(21)和式(23)來計算加載路徑的fnp. 對于一般的多軸加載情形，利用式(23)計算fnp的具體步驟如下：

1)根據輸入的軸向應變εx和剪切應變γxy，確定加載路徑形狀；

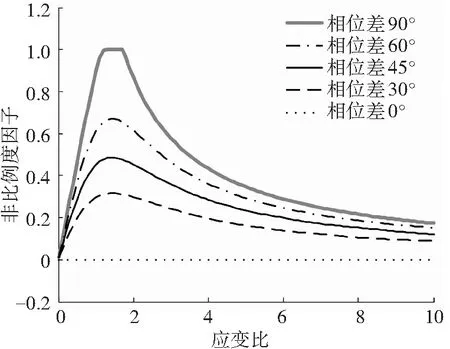
圖2 非比例度因子fnp隨應變比λ的變化

Fig.2 Correlation between the nonproportionality factor,fnp, and the strain ratio,λ

2)對于一個加載周期，以微小的時間步長Δt，將εx和γxy進行離散；

3)計算不同時刻，第i個平面(αi)上的法向應變：

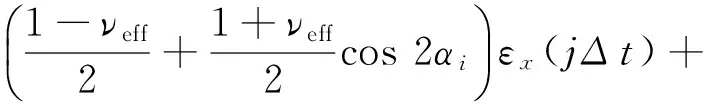
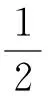
(24)

式中q表示一個循環內離散的載荷步數.

4)計算第i個平面(αi)上的法向應變范圍：

Δεn,αi=max(εn,αi(j))-min(εn,αi(j)).

(25)

5)讓i在 [0°, 180°)內以1°為步長變化，計算各平面上的法向應變范圍. 比較各平面上法向應變范圍的大小，確定最小法向應變范圍(Δεn,α)min的值；

6)利用式(21)計算相同等效應變時，圓路徑加載對應的最小法向應變范圍，即max((Δεn,α)min)；

7)利用式(23)計算加載路徑的fnp.

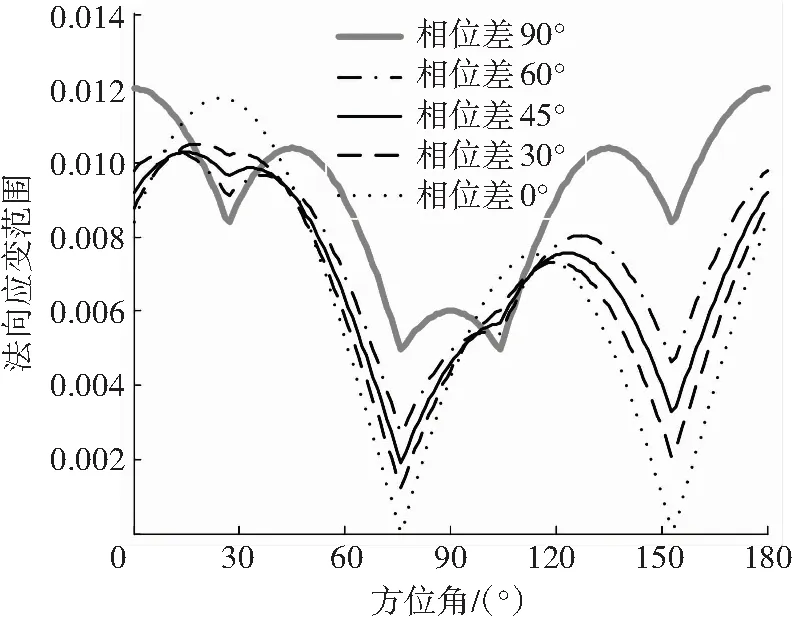
圖3 不同相位差下各平面的法向應變范圍(三角波)

Fig.3 The normal strain range,Δεn,α, of each plane under different phase delays (triangle wave)

由圖3可見，三角波加載時，相同等效應變、不同相位差下的最小法向應變范圍((Δεn,α)min)仍然隨著相位差的增大而增大，與正弦波加載時觀察到的現象一致. 因此，利用(Δεn,α)min描述加載路徑的非比例度是合理的.

為進一步驗證本文所提方法合理性，利用式(23)計算文獻[25]中14種加載路徑(具體加載路徑形狀見文獻[25])的非比例度因子，并將計算值與測量值的對比列于圖4. 由圖4可見，所提方法可以較好的計算加載路徑的非比例度因子.

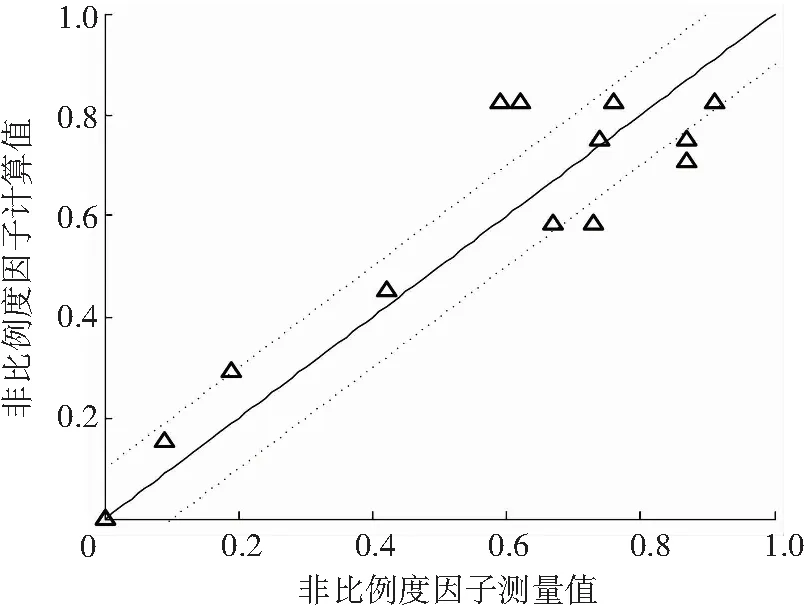
圖4 非比例度因子計算值與測量值的對比

2 試驗驗證

選用文獻[25-26]中S460N鋼和304不銹鋼在不同加載路徑下穩態應力-應變響應的試驗數據來驗證所建循環塑性本構模型的預測精度和可靠性.

2.1S460N鋼

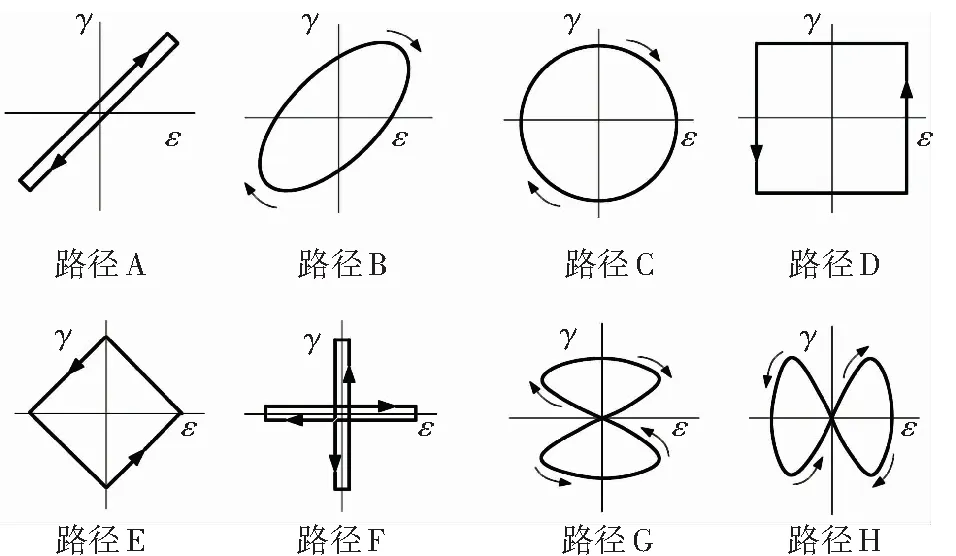
圖5 8種多軸加載路徑[26]

圖6顯示的是非比例圓路徑和比例加載路徑(包括單軸和純扭轉加載)下，S460N鋼的等效應力-等效應變關系. 由圖6可見，非比例加載路徑下S460N鋼存在附加強化現象. 根據附加強化系數αnp的定義(式(13))，由圖6可以確定S460N鋼的αnp為0.3. 利用式(23)計算得到各加載路徑下的fnp見表1.

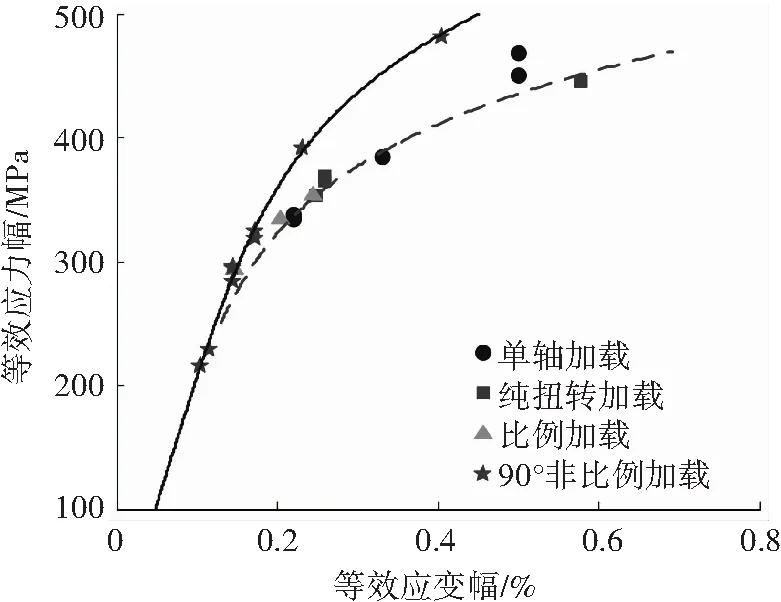
圖6比例(包括單軸和純扭轉)和非比例加載下S460N鋼的多軸循環力學行為[26]

Fig.6 Multiaxial cyclic behavior of S460N steel under proportional (including uniaxial and torsional) and non-proportional loadings[26]

表1 各加載路徑下的fnp

不同加載路徑下S460N鋼穩態循環應力-應變響應的試驗結果與預測結果的比較見圖7. 由圖7可見不同加載路徑下，模型的預測結果與試驗結果吻合較好，表明通過引入非比例度因子和附加強化系數來反映材料的非比例附加強化效應是合理的.

圖7 S460N鋼穩態應力-應變響應試驗結果與預測結果的比較(εa=0.173% and γa=0.3%)

2.2304不銹鋼

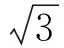
對于圖5中加載路徑D、E和F，304不銹鋼穩態循環應力-應變響應的試驗結果與預測結果的比較見圖8. 由圖8可見，不同加載路徑下，模型的預測結果與試驗結果吻合良好.

圖8 304不銹鋼穩態應力-應變響應試驗結果與預測結果的比較(εa=0.4% and γa=0.695%)

3 討 論

大量試驗結果表明，在相同等效應變下，構件非比例加載路徑下的疲勞壽命要遠小于比例加載路徑下的疲勞壽命. 從微觀角度講，非比例加載路徑下應變主軸連續旋轉，導致多滑移系開動，阻礙材料內部形成穩定的位錯結構，從而產生非比例附加強化現象，這是導致非比例加載下疲勞壽命降低的主要原因[28]. 因此，為合理的預測構件的疲勞壽命，在模擬材料的應力-應變響應時，需要考慮非比例附加強化效應的影響. 本文所建模型中，通過引入非比例度因子和附加強化系數，從加載路徑和材料本身兩個方面來考慮非比例附加強化效應的影響.

由前面的分析可知，在計算過程中，本文利用S460N鋼多軸圓路徑和比例加載路徑下的試驗結果來計算材料的附加強化系數. 在缺少試驗數據的情況下，為了仍然可以利用所建模型模擬材料的穩態應力-應變響應，需要建立附加強化系數的估算公式. Borodii等[29]通過分析25種材料的試驗結果，建立如下經驗公式來計算材料的附加強化系數：

.

(26)

式中Su和Sy分別是材料的抗拉強度和屈服強度. 由上式可知，在缺少試驗數據時，利用材料的抗拉強度和屈服強度就可以對附加強化系數進行估算.

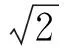
材料手冊中容易查找到材料的常規力學參量，但是對于循環強度系數K′和循環應變硬化指數n′，很多材料在手冊中并未給出. 為解決這一問題，Li等[30]利用121種合金鋼的試驗數據建立了K′和n′的估算公式：

(27)

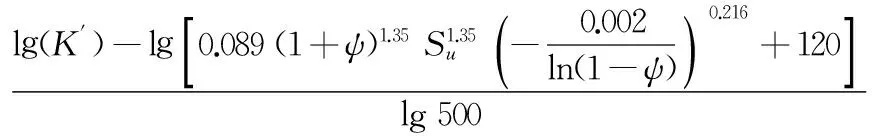
(28)

式中ψ為材料的斷面收縮率.

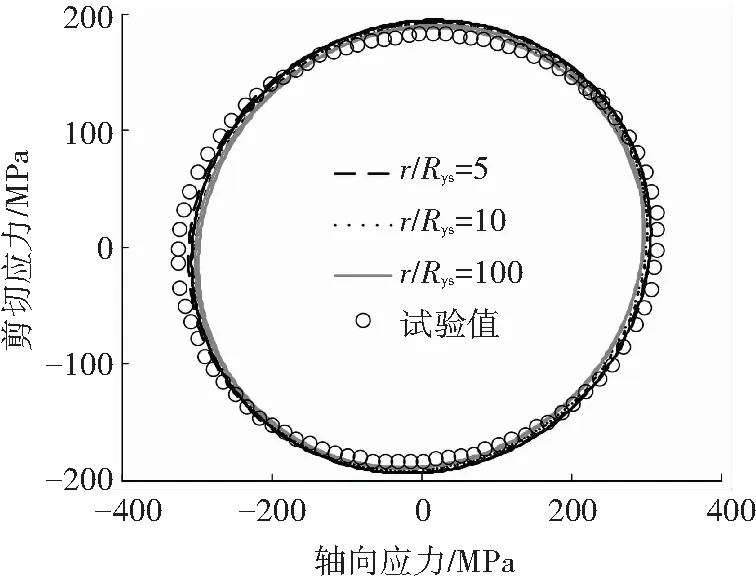
圖9 r取值對路徑C預測結果的影響

Fig.9 The predicted stress response for Path C, showing the influence ofr

根據上述估算公式(式(26)～(28))，在缺少試驗數據時，僅僅利用常規力學參量即可由本文所建本構模型來模擬多軸載荷下材料的穩態循環應力-應變響應，便于工程應用.

4 結 論

1)建立一個新的考慮非比例附加強化效應的穩態循環塑性本構模型. 應用新模型時，僅僅需要3個獨立的常規力學參量和2個疲勞參數. 而且，在缺少疲勞試驗數據時，結合文獻[29-30]中的估算公式，僅僅利用常規力學參量便可由所建模型來模擬多軸載荷下材料的穩態循環應力-應變響應，便于工程應用.

2)新模型中引入的非比例度因子和附加強化系數，從加載路徑和材料本身兩個方面來考慮非比例附加強化效應對穩態循環應力-應變響應的影響.

3)利用最小法向應變范圍，提出一種計算加載路徑非比例程度的新方法. 該方法克服了利用載荷間相位差無法描述相位差相同，應變比不同時加載路徑非比例程度的不足.

需要說明的是，所建模型適用于塑性不可壓金屬材料小變形范圍內的穩態循環應力-應變響應特性分析，并假設材料為各向同性且處于自然無變形狀態.

[1] SHAMSAEI N, FATEMI A. Effect of microstructure and hardness on non-proportional cyclic hardening coefficient and predictions[J]. Materials Science and Engineering A, 2010, 527: 3015-3024. DOI:10.1016/j.msea.2010.01.056.

[2] SOCIE D, MARQUIS G. Multiaxial fatigue[M].Warrendale: Society of Automotive Engineers Inc., 2000: 53-67.

[3] ARMSTRONG P J, FREDERICK C O. A mathematicalrepresentation of the multiaxial Bauschinger effect: RD/B/N731 [R]. Berkely: Central Electricity Generating Board, Berkely Nuclear Laboratories, 1966.

[4] CHABOCHE J L. On some modifications of kinematic hardening to improvethe description of ratcheting effects [J]. International Journal of Plasticity, 1991, 7: 661-678.

[5] 楊顯杰, 高慶, 孫訓方. 循環塑性雙曲面多軸本構模型研究[J]. 力學學報, 1993, 25(5): 569-574.

YANG Xianjie, GAO Qing, SUN Xunfang. A study on twosurface multiaxial constitutive model of cyclic plasticity [J]. Acta Mechanica Sinica, 1993, 25(5): 569-574 (in Chinese).

[6] DORING R, HOFFMEYER J, SEEGER T, et al. A plasticity model for calculating stress-strain sequences under multiaxial nonproportional cyclic loading [J].Computational Materials Science,2003,28:587-596. DOI:10.1016/j.commatsci.2003.08.015.

[7] JIANG Y, SEHITOGLU H. Modeling of cyclicratcheting plasticity, Part I: Development of constitutive relations[J]. Journal of Applied Mechanics, 1996, 63: 720-725.

[8] TANAKA E. A nonproportionality parameter and a cyclic viscoplastic constitutive model taking into account amplitude dependence and memory effects of isotropic hardening [J]. European Journal of Mechanics A/Solids, 1994, 13: 155-173.

[9] KHUTIA N, DEY P P, HASSAN T. An improved nonproportional cyclic plasticity model for multiaxial low-cycle fatigue and ratchetingresponses of 304 stainless steel[J]. Mechanics of Materials,2015, 91: 12-25. DOI: 10.1016/j.mechmat.2015.05.011.

[10]CHEN X, JIAO R. Modified kinematic hardening rule for multiaxial ratcheting prediction[J].International Journal of Plasticity, 2004, 20: 871-898. DOI:10.1016/j.ijplas.2003.05.005.

[11]MEGGIOLARO M A, WU H, CASTRO J T P. Nonproportional hardening models for predicting mean and peak stress evolution in multiaxial fatigue using Tanaka’s incremental plasticity concepts [J]. International Journal of Fatigue, 2016, 82: 146-157. DOI:10.1016/j.ijfatigue.2015.07.027.

[12]GATES N R, FATEMI A. A simplified cyclic plasticity model for calculating stress-strain response under multiaxial nonproportional loading[J].European Journal of Mechanics A/Solids,2016,59:344-355. DOI:10.1016/j.euromechsol.2016.05.001.

[13]ZHANG J. JIANG Y. Constitutive modeling of cyclic plasticity deformation of a pure polycrystalline copper[J]. International Journal of Plasticity,2008,24(10):1890-1915.DOI:10.1016/j.ijplas. 2008.02.008.

[14]WU H, MEGGIOLARO M A, CASTRO J T P. Computational implementation of a non-linear kinematic hardening formulation for tension-torsion multiaxial fatiguecalculations[J]. International Journal of Fatigue,2016,91:304-312. doi:10.1016/ j.ijfatigue.2016.01.005.

[15]SHAMSAEI N, FATEMI A, SOCIE D F. Multiaxial cyclic deformation and non-proportional hardening employing discriminating load paths [J].International Journal of Plasticity, 2010, 26: 1680-1701. DOI:10.1016/j.ijplas.2010.02.006.

[16]KRISHNA S, HASSAN T, NACEURI B, et al. Macro versus micro-scale constitutive models in simulating proportional and nonproportional cyclic and ratcheting responses of stainless steel 304[J]. International Journal of Plasticity, 2009, 25: 1910-1949. DOI: 10.1016/j.ijplas.2008.12.009.

[17]ITOH T, KAMEOKA M, OBATAYA Y. A new model for describing astable cyclic stress-strain relationship under nonproportional loading on activation state of slip systems [J]. Fatigue & Fracture of Engineering Materials and Structures, 2004,27:957-967. DOI:10.1111/j.1460-2695.00818.x.

[18]KOWALEWSKI Z L, SZYMCZAK T, MACIEJEWSKI J. Material effects during monotonic-cyclic loading [J]. International Journal of Solids and Structures, 2014, 51: 740-753. DOI: 10.1016/j.ijsolstr.2013.10.040.

[19]MADRIGAL C, NAVARRO A, CHAVES V. Biaxial cyclic plasticity experiments and application of a constitutive model forcyclically stable material behaviour[J]. International Journal of Fatigue,2016,83:240-252. DOI:10.1016/j.ijfatigue.2015.10.019.

[20]JIANG Y, KURATH P. Characteristics of the Armstrong Frederick type plastic models[J].International Journal of Plasticity, 1996, 12(3): 387-415.

[21]LI J, LI C W, QIAO Y J, et al.Fatigue life prediction for some metallic materials under constant amplitude multiaxial loading [J]. International Journal of Fatigue, 2014, 68: 10-23. DOI:10.1016/j.i jfatigue.2014.06.009.

[22]ELLYIN F, XIA, Z. A rate-independent constitutive model for transient nonproportional loading [J]. Journal of Mechanics of Physics and Solids, 1989, 37: 71-91.

[23]KANAZAWA K, MILLER K J, BROWN M W. Low cycle fatigue under out of phase loading conditions [J]. Journal of Engineering Materials and Technology, 1977, 99: 222-228.

[24]BENALLAL A, MARQUIS D. Constitutive equations for non-proportional cyclic elasto-viscoplasticity [J]. Journal of Engineering Materials and Technology, 1987, 109: 326-336.

[25]ITOH T, SAKANE M, OHNAMI M, et al. Non-proportional low cycle fatigue criterion for type 304 stainless steel [J]. Journal of Engineering Materials and Technology, 1995, 117: 285-292.

[26]HOFFMEYER J, DORING R, SEEGER T, et al. Deformation behaviour, short crack growth and fatigue lives under multiaxial nonproportional loading [J].International Journal of Fatigue, 2006, 28: 508-520. DOI:10.1016/j.ijfatigue.2005.05.014.

[27]JIANG Y, OTT W, BAUM C, et al.Fatigue life predictions by integrating EVICD fatigue damage model and an advanced cyclic plasticity theory [J]. International Journal of Plasticity, 2009, 25: 780-801. DOI:10.1016/j.ijplas.2008.06.007.

[28]朱正宇, 何國球, 張衛華,等. 非比例載荷下多軸疲勞微觀機理的研究進展[J]. 同濟大學學報(自然科學版), 2006, 34(11): 1510-1514.

ZHU Zhengyu, HE Guoqiu, ZHANG Weihua, et al. Recent advances in micromechanisms of multiaxial fatigue under nonproportional loading [J]. Journal of Tongji University (Natural Science), 2006, 34(11): 1510-1514.

[29]BORODII M V, SHUKAEV S M. Additional cyclic strain hardening and its relation to materialstructure, mechanical characteristics, and lifetime [J]. International Journal of Fatigue, 2007, 29: 1184-1191. DOI:10.1016/j.ijfatigue.2006.06.014.

[30]LI J, ZHANG Z P, LI CW. An improved method for estimation of Ramberg-Osgood curves of steels from monotonic tensile properties [J]. Fatigue & Fracture of Engineering Materials and Structures, 2016, 39: 412-426. DOI: 10.1111/ffe.12366.

Plasticconstitutivemodelformultiaxialstabilizedcyclicstress-strainresponseconsideringadditionalhardeningeffects

LI Jing, LI Chunwang, ZHANG Zhongping

(The Science Institute, Air Force Engineering University, Xi’an 710051, China)

Existing test results show that the continuous rotation of principal strain axis in cyclic deformation leading to actuation of multi-slip systems which hinders the forming of stable dislocation substructures inside the material, during nonproportional cyclic loading. As a result, the stress response under nonproportional loading will be larger than that under proportional loading. In other words, the material shows additional hardening upon nonproportional cycling. Therefore, a new constitutive model for modeling stabilized cyclic stress-strain response is proposed to consider the effect of nonproportional additional hardening based on the general form of stress-space incremental plasticity relation. In the hardening rule of the proposed model, the evolution of the back stress is simulated by introducing the nonproportionality factor,fnp, and the additional hardening coefficient,αnp, into the basic Armstrong-Frederick model. The consistency condition is enforced to obtain the relationship between the back stress and plastic modulus. Besides, a new algorithm is proposed to calculate the nonproportionality factor on the basis of the minimum normal strain range. Procedures to determine the minimum normal strain range are presented for the general multiaxial loadings. In the proposed model, the effect of nonproportional additional hardening is reflected by introducingfnpandαnp, not only on the shape of the loading path, but also on the material and its microstructure. Meanwhile, the two drawbacks of the Armstrong-Frederick model are overcome. The proposed model requires only five material constants for estimating the stabilized response. Comparisons between test results of S460N steel and 304 stainless steel and model predictions under various loading paths show that the proposed model predicts relatively accurate stress responses under both proportional and nonproportional loading paths.

nonproportional additional hardening; stabilized cyclic stress-strain response; plastic constitutive model; nonproportionality factor; additional hardening coefficient

10.11918/j.issn.0367-6234.201612058

O344

A

0367-6234(2017)11-0143-08

2016-12-12

國家自然科學基金(51601221, 51575524)；陜西省自然科學基礎研究計劃(2015JM5240)；空軍工程大學理學院博士科研啟動資金

李 靜(1985—)，男，博士，講師

李 靜，lijing02010303@163.com

(編輯苗秀芝)