壓縮感知的天文圖像去噪算法
張 杰, 朱 奕, 史小平
(哈爾濱工業大學 控制與仿真中心, 哈爾濱 150080)
壓縮感知的天文圖像去噪算法
張 杰, 朱 奕, 史小平
(哈爾濱工業大學 控制與仿真中心, 哈爾濱 150080)
針對壓縮感知迭代收縮閾值算法在圖像處理中存在收斂速度慢和去噪性能差的缺陷,提出了一種改進的高性能迭代收縮閾值天文圖像去噪重建算法.首先,使用經典最速下降法中的BB線性搜索步長算子加快迭代收縮閾值算法的收斂速度;其次,為了進一步提高重構天文圖像的質量,在傳統VisuShrink收縮閾值的基礎上,提出一種下降VisuShrink收縮閾值對圖像信息進行篩選;由于閾值去噪方法在迭代重建的過程中會導致重建的圖像中出現偽吉布斯效應,最后采用循環平移的方法在每次迭代過程中對獲取的重建圖像進行調整. 多次的試驗結果表明,與傳統的壓縮感知迭代收縮閾值算法相比,所提出的算法不僅能夠獲得較優的去噪性能和較快的收斂速度,同時可以有效地保護天文圖像的特征和紋理等細節信息.此外,當選取的壓縮采樣比較低時,本算法也可以獲得相對較高的峰值信噪比和視覺質量,進一步驗證了本算法在天文圖像去噪中的有效性.
收縮閾值; 天文圖像; 去噪; 壓縮感知; 循環平移
利用天文圖像對外太空進行研究是深空探索的一個重要分支.從獲得的天文圖像可以直接得知某一星體上的地表結構,是否存在未知生命等重要信息.為了能夠獲得更多的天文信息,天文圖像的采集一般都是采用高分辨率CMOS/CCD傳感器,但是衛星或者其他的深空探測設備所攜帶的存儲空間有限,存儲這些高分辨率圖像將會給有限的存儲空間帶來較大壓力.為解決這一難題,天文圖像在存儲之前通常都要經過壓縮處理.然而常用的JPEG/JPEG-2000方法[1-3]很難獲得較低的圖像壓縮采樣比.
另一方面,由于環境、拍攝條件等因素的影響,天文圖像在采集和傳輸的過程中經常受到噪聲信號的干擾,在地面接收站接收到的天文圖像通常含有噪聲.從接收到的圖像中很難分辨出某一區域的實際地形特征.因此在接收到這些天文圖像后,通常要進行去噪處理.然而目前大部分的去噪方法經常由于很難從高維數的信號觀測值中獲得足夠有效的圖像信息,導致重構信號的質量較差[4-5].為有效解決高維數信號的重建問題,學者們一直在探索如何從高維數信號中獲得一種低維的信號結構,同時保證原始信號能從這種低維結構中獲得精確重建.即,從信號中提取重要的信息同時舍棄非重要信息,直接使用這些重要信息重建高維數信號.近幾年提出的信號稀疏性[5-6]可能是探索信號低維結構的一種比較簡單方法.
基于信號的稀疏性,Donoho[7]提出了著名的壓縮感知(compressed sensing,CS)理論.該理論一經提出,就引起了各領域的極大關注.它指出:如果信號在某一稀疏變換基上是稀疏的,則可以使用一個與該稀疏基不相關的低維測量矩陣對原信號進行觀測,同時使用某一CS重建算法就可以從獲得的少量信號觀測值中精確重構原始信號.可以看出,信號在采集的同時就已經完成了壓縮過程.傳統的奈奎斯特/香農采樣定理要求信號的采樣速率必須大于或者等于兩倍的信號帶寬才能夠精確重建原始信號,但是采樣速率在低于兩倍的信號帶寬時,CS方法仍可以精確重建原始信號.因此,CS理論可以有效地解決高維數信號的重建問題,本文將其應用到高分辨率天文圖像去噪中.
CS理論主要包含3個部分:稀疏變換、測量矩陣和重建算法.本文主要關注于如何設計一個高性能的重建算法.經過近幾年的努力,學者們提出了許多的重建算法,例如線性規劃類算法[8-9]、迭代收縮閾值類(iterative shrinkage thresholding,IST)算法[10-12]、梯度下降類方法[13]和貝葉斯類方法[14]等.在這些算法當中,IST算法設計簡單且易于實現,更重要的是大部分的稀疏基都能較容易地應用到IST框架當中.這些優勢使得IST算法經常受到學者們的青睞.然而該算法的收斂速度較慢,去噪性能也需要進一步提高.
為了提高梯度下降法的收斂速度,Barzilai等[15]提出了著名的BB線性搜索步長,并取得較快的收斂效果.本文將其應用到IST算法中調節其收斂速度.在圖像去噪中,通常采用閾值去噪方法對圖像信息進行篩選,本文提出一種下降VisuShrink收縮閾值篩選天文圖像信息.閾值去噪雖然設計簡單且能獲得較好的去噪效果,但在奇異點(如邊緣或者紋理)附近會出現較大的幅值振蕩,最終導致重構的圖像出現偽吉布斯現象[16].循環平移方法[17-18]可有效地減小或者消除這種幅值振蕩,提高重構圖像質量.本文將其應用到IST算法中,在迭代過程中對重構的天文圖像進行調整.基于上述技術,本文提出了高性能的IST改進算法.實驗結果表明,該算法可以以較快的收斂速度重構一幅清晰的天文圖像.當壓縮采樣比較低時,該算法也具有較好的重建性能.
1 壓縮感知去噪模型
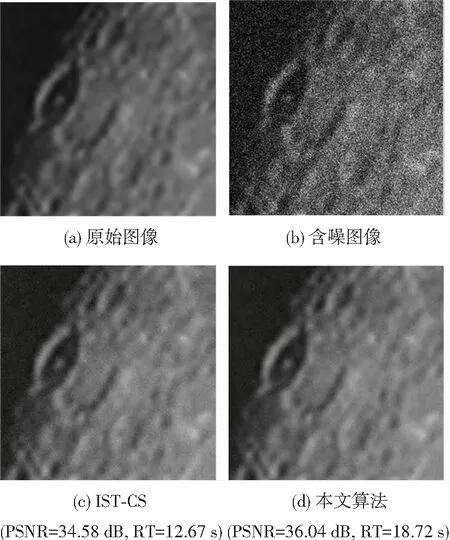
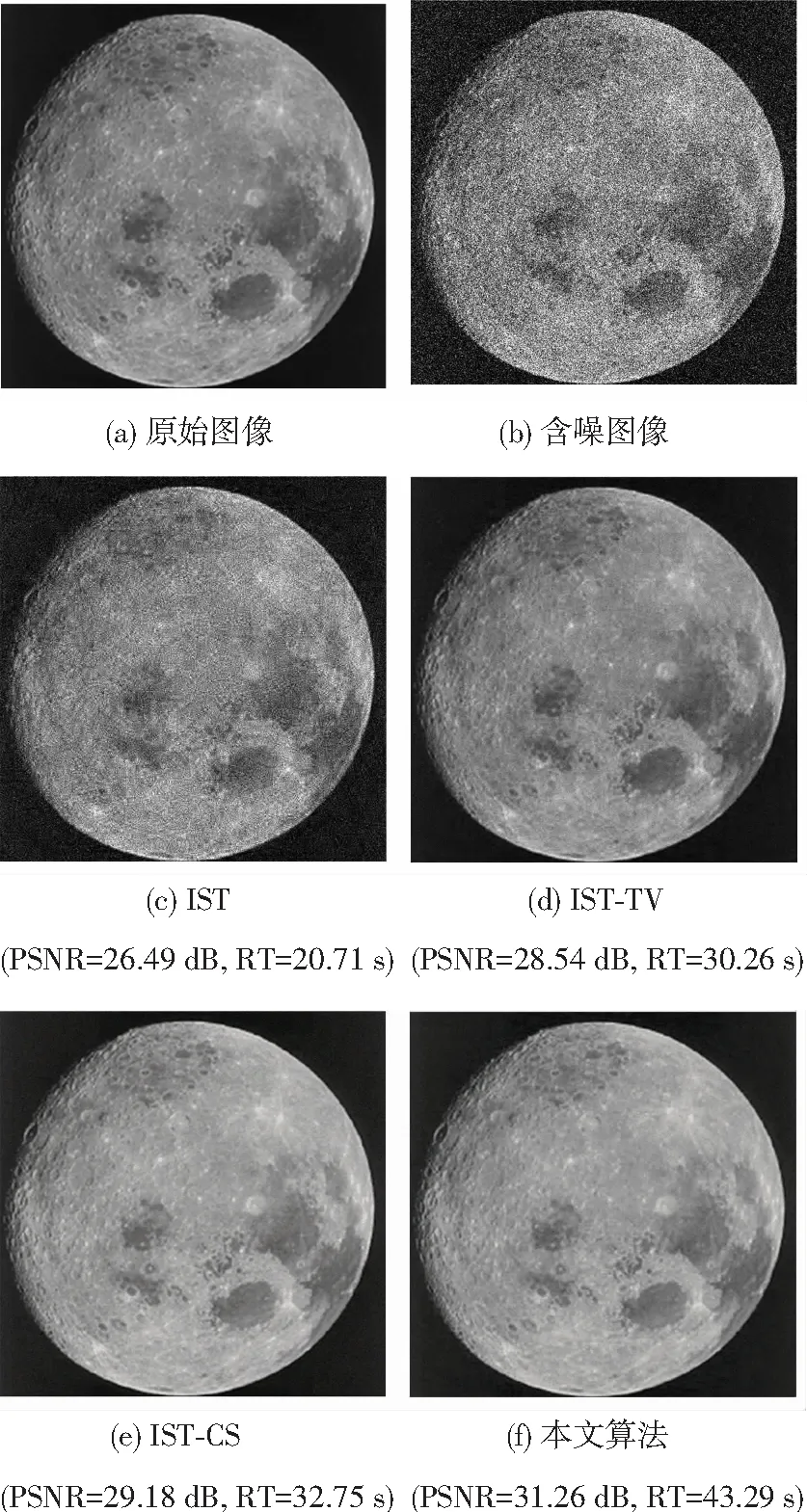
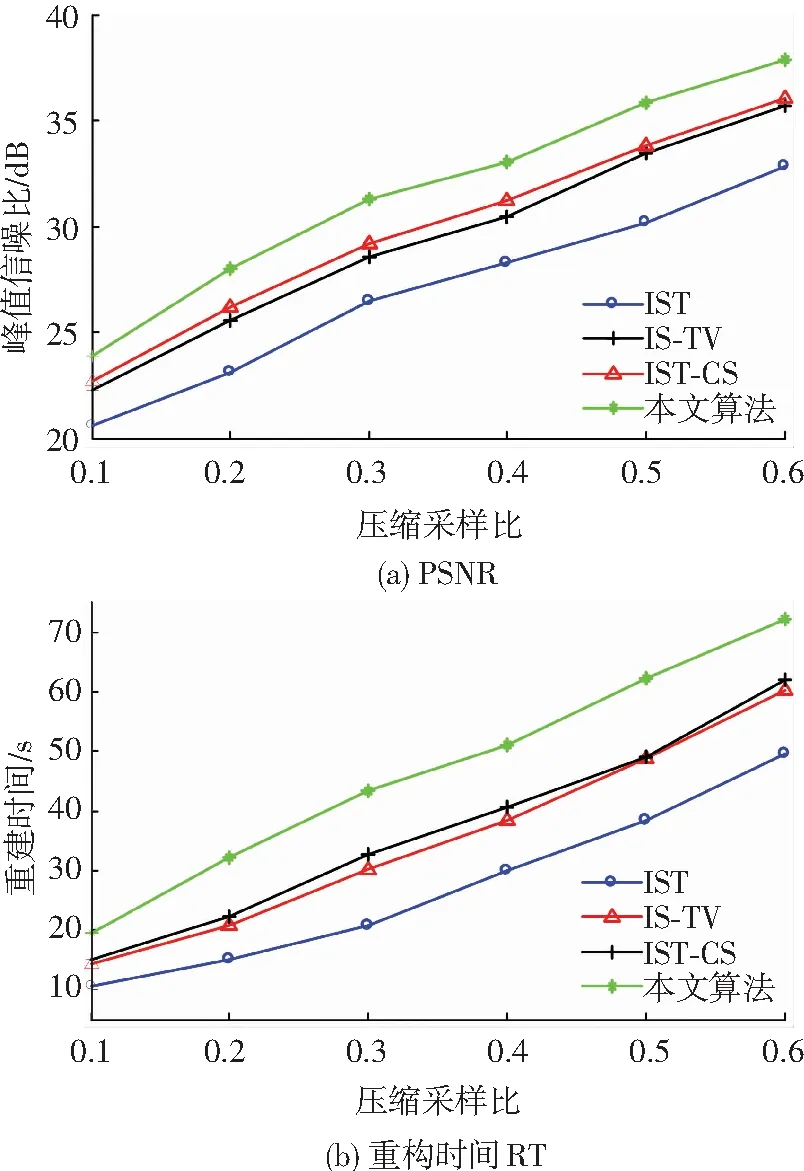
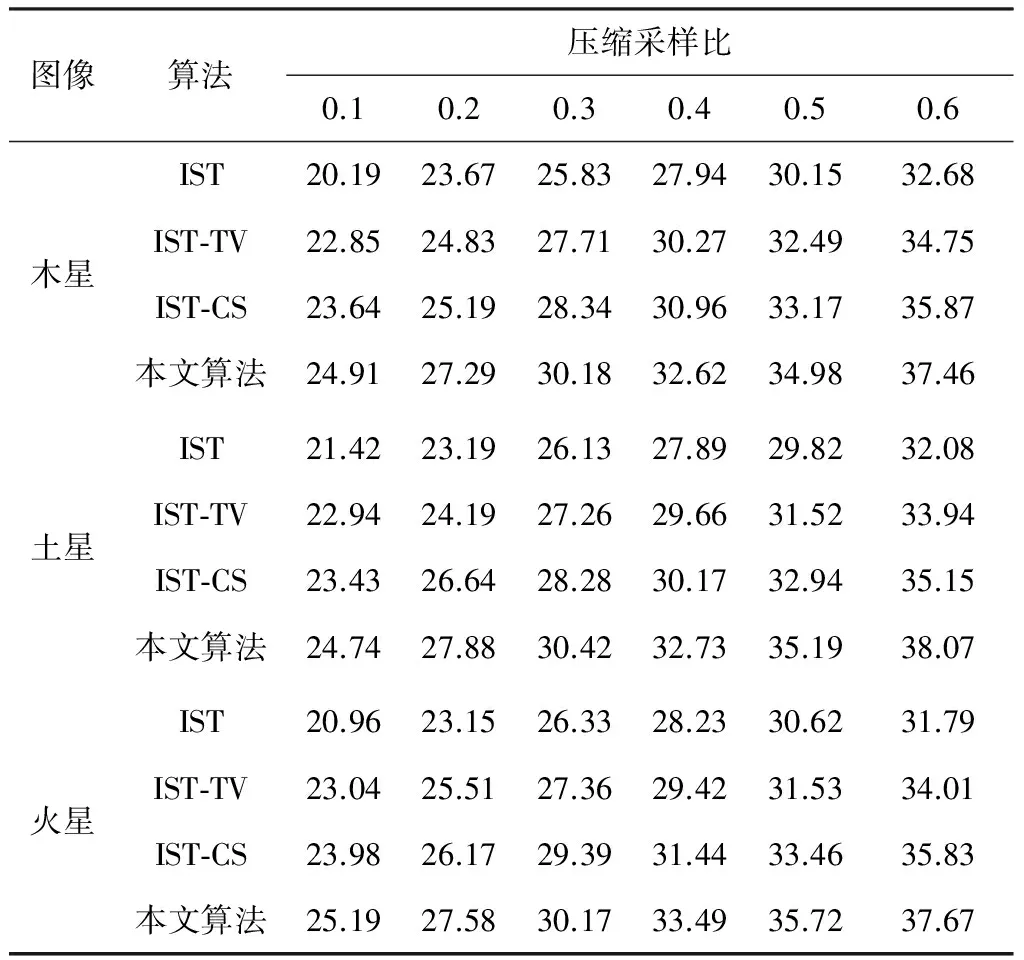
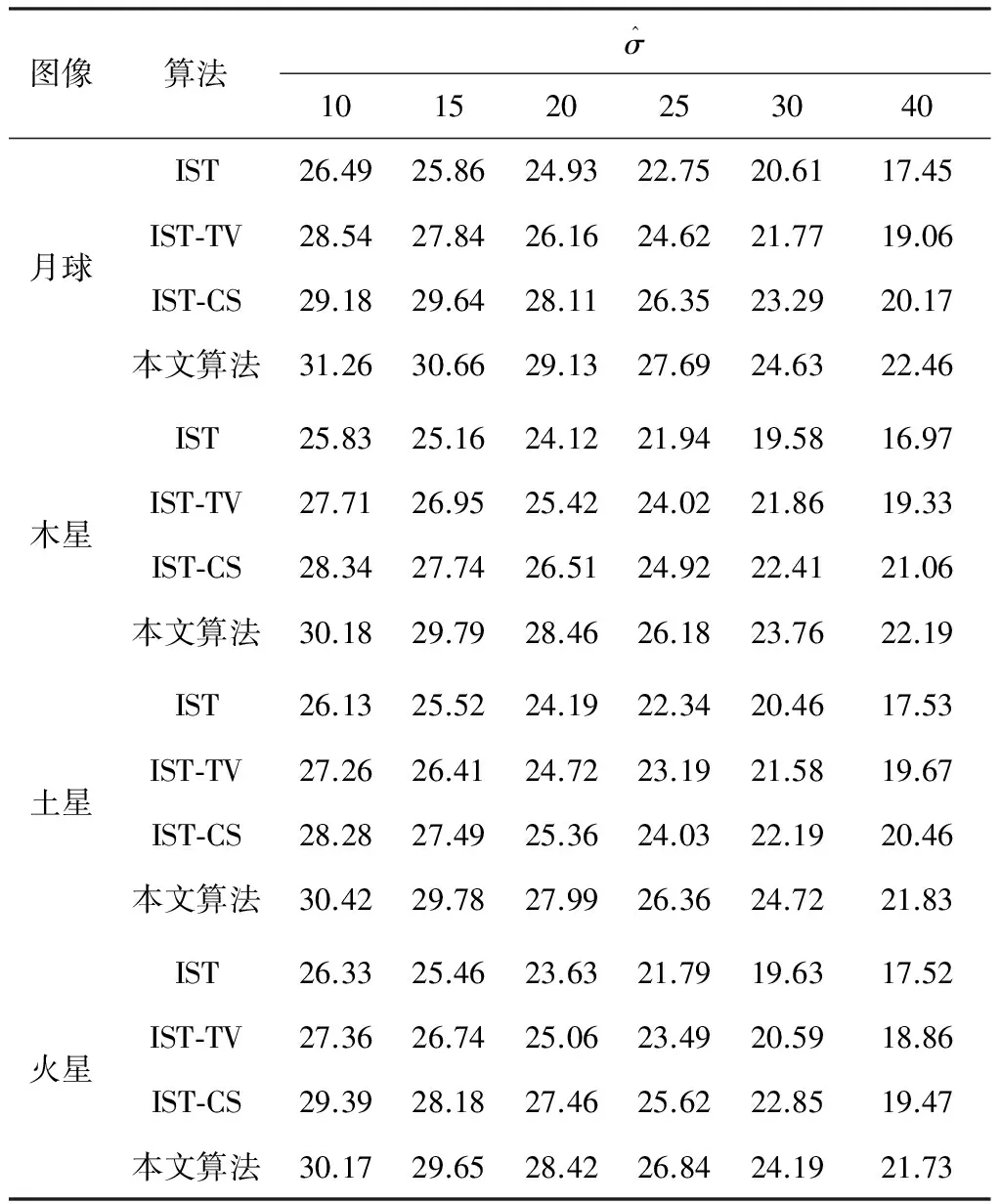
假設某一N×1信號x是K-稀疏的[6-7],則可以用一個低維非自適應矩陣(又稱為測量矩陣)Ф∈RM×N(M< y=Φx+e. (1) 從式(1)可以看出,由于M< y=Φx+e=ΦΨΨ-1x+e=Θs+e, (2) 式中s=Ψ-1x為稀疏系數.這里Θ=ΦΨ可以作為CS測量矩陣直接對s進行觀測.測量矩陣Ф要求與稀疏基Ψ不相關,兩者越不相關,需要的測量次數就越少,則可以獲得更低的信號壓縮采樣比. 具有稀疏限制的l1范數最小化方法經常用來求解CS問題(2),即 或者轉化為對稀疏系數s的求解,可表示為 式中第1項代表懲罰項,用來估算計算值與觀測值之間的偏差;第2項為正則化項,表示原始信號的先驗知識. 經典的IST算法迭代過程可描述為 xk+1=xk+HS(μkΦT(y-Φxk)). 式中:μk為線性搜索步長,為了計算方便通常設定為1,雖然簡化了計算,但影響了算法的收斂速度;HS(·)表示閾值算子,通常考慮為硬閾值算子.其中 式中:q為迭代索引;Q為最大迭代次數.當q=0時,T為通用閾值. 2.1 BB線性搜索步長 最速下降法[20]的迭代過程可表示為 xk+1=xk-μkfk. (3) 式中:fk=f(xk)為任一目標函數Γ在位置xk處的梯度向量;μk>0為線性搜索步長,它要求滿足以下條件: ). fk=ΦT(Φxk-f), 和經典的SD迭代步長算子為 為了獲得高性能的步長算子,文獻[15]用前一次的迭代信息設定當前迭代所使用的步長算子,同時修改了式(3)的迭代過程,即 xk+1=xk-Dkfk, 式中Dk=μkI.其中I為單位向量.為了保證它具有某種擬牛頓特性,需要滿足以下任一限制條件: 文獻[20]證明了BB步長算子比SD步長算子更能有效地提升最速下降法的收斂速度.本文將BB步長算子應用到IST算法中調節其收斂速度. 2.2 循環平移方法 在圖像去噪的過程中,當一幅圖像包含有較多奇異點時,將會遇到如下問題:對于某一個奇異點具有較好去噪效果的平移量可能對另一個奇異點去噪效果較差.因此,對于包含較多紋理和邊緣特征的天文圖像,就很難獲得針對所有奇異點都具有較好去噪效果的最佳平移量.循環平移方法可有效解決這一難題,其循環平移過程可描述為 式中K1、K2分別為沿行和列方向的最大平移量.在小波變換中,如果測試一幅N×N圖像x且N=2K,則認為K1=K2=K為最大平移量.Ci,j(x)為定義的循環平移算子,對于二維圖像x(m,n),可定義為 Ci,j(x)=x[mod(m+i)/N,mod(n+j)/N)]. C-i,-j(x)為Ci,j(x)的逆過程,可表示為 C-i,-j(x)=[Ci,j(x)]-1. 此外,S(x)為小波變換過程,S-1(x)為小波逆變換.θ(x)為閾值函數,本文將其考慮為硬閾值函數HS(x),并且閾值T為下降VisuShrink收縮閾值. 2.3 本文算法 綜上所述,本文算法的設計步驟概括如下: 10 月29 日上午,由山東省旅游飯店協會和山東新業態旅游住宿業分會主辦的首屆山東省文化主題飯店發展論壇在泰安銘座三泰賓館開幕。會場內“大腕”云集,在一天的時間里,業內實踐專家圍繞有關文化、生活、酒店三個議題展開了討論,共謀文化主題酒店的未來發展路徑。 1)初始化過程.初始化迭代索引q=0,最大迭代次數Q=30和重構圖像xq=0. 2)計算下降VisuShrink收縮閾值和BB步長算子μq. 3)使用下式更新估計值. xq+1=xq+HS(μqΦT(y-Φxq)). 4)對重構的圖像進行循環平移,可表示為 ). 6)q=q+1.如果q=Q,輸出重構圖像;否則,進入步驟2). 從圖1可以看出,與其他算法相比,本文算法能獲得較好的視覺質量和較高的峰值信噪比(PSNR),但花費的重構時間(reconstruction time,RT)較長.同時可以看出,IST-TV、IST-CS和本文算法都能有效地抑制偽吉布斯效應. 設定噪聲標準差和壓縮采樣比不變,如圖3所示不同算法隨迭代次數增長獲得的PSNR值.可以看出,本文算法具有比其他算法更快的收斂速度. 圖1 不同算法重構得到的結果 圖2 不同算法重構得到變化曲線 圖3 不同迭代次數下獲得的PSNR 圖4 不同算法獲得的重構結果 表1 壓縮采樣比變化時獲得的PSNR 1)本文將壓縮感知理論應用到天文圖像去噪,并在迭代收縮閾值算法的基礎上,提出了一種高性能改進算法.該算法首先使用BB步長算子調節收斂速度;其次使用提出的下降VisuShrink閾值對重構圖像進行篩選;最后對重建圖像進行循環平移以消除偽吉布斯效應. 2)本文算法與IST、IST-TV和IST-CS算法的對比分析結果表明,本文算法可以以較快的收斂速度重構一幅清晰的天文圖像,并且能有效地保護天文圖像的細節特征.在壓縮采樣比較低時,本文算法也可獲得較優的重構效果. 3)雖然本文算法的收斂速度和去噪重建性能得到很大的提高,但是花費的重建時間較長,因此如何提高本文算法的重建速度是以后改進的方向. 圖5 兩種算法重構結果對比 Fig.5 Comparison of the reconstructed result between two algorithms [1] SKODRAS A, CHRISTOPOLOS C, EBRAHIMI T. The JPEG 2000 still image compression standard[J]. IEEE Signal Processing Magazine, 2001, 18(5): 36-58.DOI: 10. 1109/79.952804. [2] WALLANCEG K. The JPEG still picture compression standard[J]. IEEE Transactions on Consumer, 2002, 38(1): 18-34. DOI: 10.1109/30.125072. [3] SHI Xiaoping, ZHANG Jie. Reconstruction and transmission of astronomical image based on compressed sensing[J]. Journal of Systems Engineering and Electronics, 2016, 27(3):680-690.DOI: 10.1109/JSEE.2016.00071. [4] ELDARY C, KUTYNIOK G. Compressed sensing: theory and applications[M]. New York: Cambridge University Press, 2012:1-515. [5] BENEDETTO J J. Compressed sensing and its applications[M]. USA: Birkhauser, 2013:97-143. [6] CANDES E, ROMBERG J. Sparsity and incoherence in compressive sampling[J]. Inverse Problems, 2007, 23(3): 969-985.DOI:10.1088/0266-5611/23/3/008. [7] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.DOI: 10.1109/TIT.2006.871582. [8] CANDES E J, TAO T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2009, 51(12): 4203-4215.DOI:10.1109/TIT.2005.858979. [9] FIGUEIREDOM A T, NOWAK R D, WRIGHT S J. Gradient Projection for sparse reconstruction: application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007,1(4):586-597.DOI:10. 1109/JSTSP.2007.910281. [10]BLUMENSATH T, DAVIES M E. Iterative hard thresholding for compressed sensing[J]. Applied and Computational Harmonic Analysis, 2009, 27(3):265-274. DOI:10.1016/j. acha.2009.04.002. [11]CAI Jianfeng, OSHER S, SHEN Zuowei. Linearized bregman iterations for compressed sensing[J]. Mathematics of Computation, 2009, 78(267): 1515-1536. DOI:10.1090/S0025-5718-08- 02189-3. [12]DAUBECHIES I, DEFRISE M, MOL C D. An iterative thresholding algorithm for linear inverse problems with a sparisity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11):1413-1457.DOI:10.1002/ cpa.20042. [13]GARG R, KHANDEKAR R. Gradient descent with sparsification: an iterative algorithm for sparse recovery with restricted isometry property[C]//Proceedings of the 26th Annual International Conference on Machine Learning. New York, NY: ACM, 2009: 337-344. DOI:10.1145/1553374.1553417. [14]JI Shihao, XUE Ya, CARIN L. Bayesian compressive sensing[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2346-2356. DOI: 10.1109/TSP.2007.914345. [15]BARZILAI J, BORWEIN J M. Two point step size gradient methods[J]. IMA Journal of Numerical Analysis, 1988, 8(1):141-148.DOI: 10.1093/imanum/8.1.141. [16]王蓓,張根耀,李智,等. 基于新閾值函數的小波閾值去噪算法[J].計算機應用,2014, 34(5): 1499-1502.DOI:10. 11772/j.issn.1001-9081.2004.05.1499. WANG Pei, ZHANG Genyao, LI Zhi, et al. Wavelet threshold denoising algorithm based on new threshold function[J]. Journal of Computer Applications, 2014, 34(5): 1499-1502.DOI: 10.11772/j.issn.1001-9081.2004.05.1499. [17]BINHN T, KHARE A. Multilevel threshold based image denoising in curvelet domain[J]. Journal of Computer Science, 2010, 25(3): 632-640. DOI:10.1007/s11390- 010-9352-y. [18]郭海濤,趙紅葉,徐雷,等. 基于循環平移和DTCWT的聲吶圖像濾波方法[J]. 儀器儀表學報,2015,36(6): 1351-1356.DOI: 10.3969/j.issn.0254-3087.2015.06.020. GUO Haitao, ZHAO Hongye, XU Lei, et al. Sonar image filtering method based on cycle shift and DTCWT[J]. Chinese Journal of Scientific Instrument, 2015,36(6): 1351-1356.DOI: 10.3969/j.issn.0254-3087.2015.06.020. [19]CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI: 10.1109/ TIT.2005.862083. [20]YUAN Yaxiang. A new stepsize for the steepest descent method[J]. Journal of Computational Mathematics, 2006, 24(2):149-156.DOI: 10.1063/1.4882499. Compressedsensingdenoisingalgorithmforastronomicalimage ZHANG Jie, ZHU Yi, SHI Xiaoping (Control and Simulation Center, Harbin Institute of Technology, Harbin 150080, China) In the deep space exploration, astronomical image acquisition, transmission and processing have always been the focus of research. To solve problems of slow convergence speed, poor denoising performance in compressed sensing iterative shrinkage-thresholding algorithm for image processing, an improved iterative shrinkage-thresholding astronomical image denoising and reconstruction algorithm with high performance is proposed. Firstly, the BB linear search stepsize of the classical steepest descent algorithm is used to accelerate the convergence speed of iterative shrinkage-thresholding algorithm; secondly, to further improve the reconstructed astronomical image quality, based on the classical VisuShrink shrinkage-threshold, a decreasing VisuShrink shrinkage-threshold is proposed to select the image information; since the pseudo-gibbs effect caused by threshold denoising method will appear in the process of image reconstruction, the cycle spinning method is finally employed to adjust the reconstructed image in each iteration. Multiple experimental results show that, compared with the traditional compressed sensing iterative shrinkage-thresholding algorithm, the algorithm proposed can not only obtain better denoising performance and faster convergence speed, but also effectively protect the astronomical image detail information, such as feature and texture. In addition, when compression sampling ratio is lower, the algorithm proposed also can obtain relatively higher peak signal to noise ratio and visual quality, proving the effectiveness of the algorithm proposed for astronomical image denoising. shrinkage-threshold; astronomical image; denoising; compressed sensing; cycle spinning 10.11918/j.issn.0367-6234.201609002 TN911.73 A 0367-6234(2017)10-0078-05 2016-09-01 國家自然科學基金(61074127) 張 杰(1986—),男,博士研究生; 史小平(1965—),男,教 授,博士生導師 史小平,sxp@hit.edu.cn (編輯張 紅)2 高性能IST算法
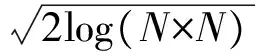
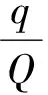
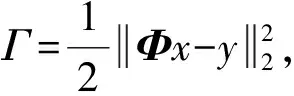
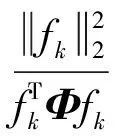
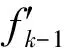
3 實驗及分析
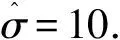
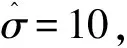


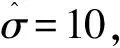
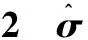

4 結 論