動態融合復雜網絡節點重要度評估方法

付 凱，夏靖波，趙小歡

(1.空軍工程大學 信息與導航學院，西安710077； 2. 95246部隊，南寧530003； 3.廈門大學 嘉庚學院，福建 漳州363105； 4. 95340部隊，廣西 百色 533616)

動態融合復雜網絡節點重要度評估方法

付 凱1,2，夏靖波3，趙小歡4

(1.空軍工程大學 信息與導航學院，西安710077； 2. 95246部隊，南寧530003； 3.廈門大學 嘉庚學院，福建 漳州363105； 4. 95340部隊，廣西 百色 533616)

為挖掘復雜網絡中的關鍵節點及提高網絡魯棒性，針對有/無線多網融合的層級網絡，提出了動態融合復雜網絡模型及其節點重要度評估方法.結合動態融合復雜網絡的特點，定義了邊連通概率、路徑連通概率、網絡連通概率、融合節點比例、融合節點分布和融合路徑比例等與網絡動態性和融合性相關的參數.在單層復雜網絡節點重要度評估指標的基礎上，設計了融合網絡節點度中心性、節點介數中心性和節點融合中心性指標.其中，融合節點的節點融合中心性表示融合節點對網絡融合的貢獻程度，非融合節點的節點融合中心性表示非融合節點對網絡融合的輔助作用程度，主要體現在作為融合節點之間的中繼節點.最后，綜合考慮網絡拓撲結構、動態融合特性等因素進行節點重要度評估.以改進的動態交織風箏網絡為例進行仿真分析，結果表明該方法能夠比較全面地刻畫節點在動態融合復雜網絡中的重要性.利用NS2搭建由光通信網和衛星通信網融合構成的仿真實驗網絡，進一步驗證了在仿真網絡環境中本方法的有效性.

復雜網絡；動態融合；節點重要度；度中心性；介數中心性；融合中心性

復雜網絡小世界效應[1]和無標度特性[2]的發現，掀起了國內外研究復雜網絡的熱潮.隨著網絡科學[3-4]的蓬勃發展，節點重要度評估進一步受到研究人員的關注，尋找復雜網絡中的關鍵節點成為網絡科學的重要研究內容.目前，節點重要度評估方法主要包括基于網絡結構的方法和基于傳播動力學的方法[5].度中心性、介數中心性[6]、特征向量中心性[7]等是典型的基于網絡結構的評估指標，其依據是網絡局部或全局屬性信息.基于傳播動力學的方法通過計算網絡中節點的影響范圍來衡量其重要度，如社會網絡中關鍵節點的挖掘[8-9].上述評估指標主要針對單層復雜網絡，隨著研究的深入和應用的拓展，多種層級復雜網絡模型[10]被相繼提出.相互依存網絡[11]描述了具有相互影響和依賴關系的網絡模型，對于預防和控制復雜系統中的相繼故障具有重要意義，如電力-計算機網等.陳宏斌等[12]提出了二元隨機網的概念，它是一種特殊的二元網，不考慮同類節點之間的相互作用，如圖書借閱網絡等.邵峰晶等[13]提出多子網復合網絡模型，通過網絡加載和拆分等網絡運算進行網絡的復合與分解，實現復雜網絡中同一子網元素間、不同子網元素間以及不同子網之間的相互關系等形式描述.超網絡[14]是一種“高于而又超于現存網絡”的網絡，用以描述規模巨大、連接復雜、具有嵌套網絡的大型復雜網絡，如供應鏈網絡等.以上層級復雜網絡側重不同子網之間的相互關系，而對于網絡模型中的節點重要性未做深入研究.沈迪等[15]提出一種交織型層級復雜網，描述由兩個具有部分相同節點、連接邊屬性近似的子網構成的層級復雜網絡，并且定義了相關測度用于衡量子網之間的密切程度及節點中心性，但只適用于靜態網絡.而節點重要度評估問題已逐漸向動態變化的時變網絡延伸，在拓撲結構變化的網絡中發現關鍵節點更具有挑戰性[16]. Basaras等[17]在介數和K-SHELL基礎上提出了動態復雜網絡中的關鍵節點發現算法，基于局部信息從而降低計算開銷，更加適合動態網絡中應用. Masaki[18]以動態變化的社會網絡為背景，提出了加權動態復雜網絡中的節點重要度評估方法.

隨著對網絡應用的需求不斷增強，多網系融合、有/無線并用成為未來網絡的發展趨勢.例如，手機、平板電腦等移動網絡終端通過無線路由器實現對互聯網的接入，就構成了有線的寬帶互聯網與無線的手機通信網之間的融合互聯，而且網絡帶寬、信號強度等使得有線和無線信道的通信質量存在差異.為了在這種融合網絡中發現關鍵節點、優化網絡結構等，需要構建新的網絡模型研究節點重要度評估問題.本文在文獻[15]的基礎上提出動態融合復雜網絡(dynamic convergence complex networks，DCCN)模型，定義了與動態性和融合性相關的網絡參數，結合網絡動態融合特性改進了節點度中心性和介數中心性指標，并提出了節點融合中心性以反映各類節點對促進網絡融合的貢獻程度，在此基礎上進行動態融合復雜網絡節點重要度評估，最后通過仿真分析驗證了方法的有效性.與現有模型相比，本文模型結合當前有/無線網絡融合發展的需求，在融合網絡的基礎上又考慮了網絡動態特性，并結合網絡動態融合特性設計或改進節點中心性指標，能夠比較全面地刻畫節點在動態融合復雜網絡中的重要性.

1 動態融合復雜網絡模型

1.1 理論基礎

設圖Ga=Va,Ea是一個無環無向無權的單層復雜網絡，Va={v1,v2,…,vn}表示網絡a的節點集合，節點數量為Va=n，Ea={e1,e2,…,em}=Va×Va為網絡a的邊集合，邊的數量為Ea=m.A=Aijn×n為網絡a的鄰接矩陣，取值為0或1，表示節點之間是否存在連接邊.在圖Ga中任意兩個節點之間最長的路徑稱為圖Ga的直徑，記為Dnd.

在單層復雜網絡中，節點vi的度中心性定義為

式中:gi為節點vi的度，n為網絡的節點數.

節點vi的介數中心性定義為

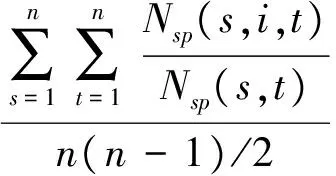
(1)

式中:Nsp(s,t)為節點vs和vt之間的最短路徑數量，Nsp(s,i,t)為節點vs和vt之間經過節點vi的最短路徑數量.

1.2 模型概述

定義1動態融合復雜網絡.由兩種以上單層復雜網絡融合而成，且其中至少有一種為動態網絡的層級網絡稱為動態融合復雜網絡.動態融合復雜網絡中的“動態”是指網絡中的邊以一定概率進行連通(主要指無線傳輸手段等間歇連接)，而節點數量保持不變.網絡動態性對介數等與路徑相關的參數影響較大，而對度等基于網絡局部屬性的參數影響較小.動態融合復雜網絡中的“融合”是指多個網絡之間存在部分節點復用，節點之間可能存在兩種以上屬性的邊.為方便研究，本文僅考慮由兩種單層復雜網絡組成的動態融合復雜網絡，且其中一種為動態網絡.

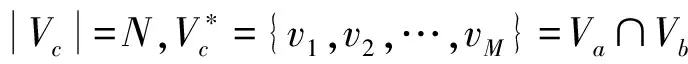
1.3 參數定義

動態融合復雜網絡最重要的特性是動態和融合，因此本文主要從動態和融合兩方面設計網絡參數.其中，網絡連通參數主要包括邊連通概率、路徑連通概率和網絡連通概率，用以描述網絡的連通狀況；網絡融合參數主要包括融合節點比例、融合節點分布和融合路徑比例，用以描述網絡的融合程度.

1.3.1 邊連通概率

在動態網絡中，如果節點vi和vj之間存在連接邊，則Pij表示該邊的連通概率，并假定非動態網絡中邊的連通概率為1.令P=PijN×N為融合網絡c的連通性矩陣，規定節點之間無連接邊時取值為0，節點之間有1條邊時為該邊的連通概率，節點之間有2條邊時取2條邊的連通概率的最大值.

1.3.2 路徑連通概率

設路徑vi-vm-vn-…-vz-vj，則Qij(k)=Pim×Pmn×…×Pzj表示該路徑的連通概率，為該路徑上所有邊的連通概率之積.值得注意的是，Qij(k)=Pim×Pmn×…×Pzj表示特定的一條路徑(vi-vm-vn-…-vz-vj，其路徑編號為k)的連通概率，而不是指節點vi和vj之間的路徑連通概率，因為節點vi和vj可能存在多條路徑(路徑編號k取不同的值)，而每一條路徑都對應一個路徑連通概率.

1.3.3 網絡連通概率

網絡連通概率定義為

反映整個網絡的平均連通狀況.

1.3.4 融合節點比例

融合節點比例定義為

Rcnp=M/N，

表示網絡節點集中融合節點所占的比例，從融合節點數量的角度反映網絡融合程度，融合節點越多則越能促進網絡的融合.

1.3.5 融合節點分布

融合節點比例在一定程度上反映了網絡的融合程度，但還存在片面性.如果融合節點比較密集地分布在局部區域，那么與融合節點分散分布的情形相比，其對促進整個網絡融合的作用會減弱.因此，定義融合節點分布為

Rcnd=Davg/Dnd，

表示網絡中融合節點的緊密程度，從融合節點位置的角度反映網絡融合程度，融合節點在網絡中的位置越分散則越能促進網絡的融合.其中，Davg為融合節點之間的平均距離，Dnd為融合網絡的直徑.

1.3.6 融合路徑比例

融合路徑比例定義為

Rcpp=Ncp/Nsp，

表示最短路徑中融合路徑所占的比例，從消息傳播的角度反映網絡融合程度，融合路徑越多則越能促進網絡的融合.其中，Nsp為網絡中所有節點對之間的最短路徑的數量，Ncp為這些最短路徑中融合路徑的數量.融合路徑是指包含兩種邊的路徑，僅包含融合節點但只有一種邊的路徑不是融合路徑.如圖1所示，對于路徑1-2-3-4，圖1(a)、(b)為融合路徑，而圖1(c)不是融合路徑.

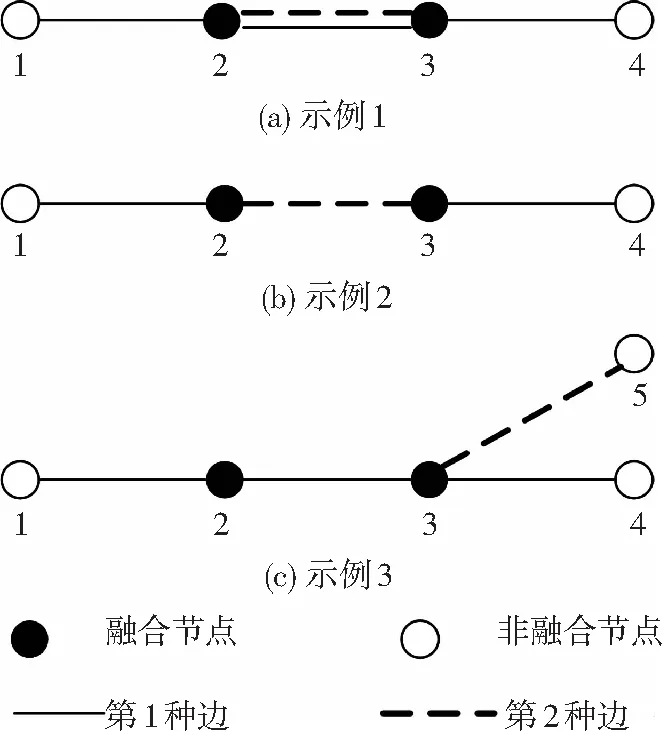
圖1 融合路徑示例

2 節點重要度評估方法

動態融合復雜網絡的節點重要度評估主要是在網絡拓撲結構的基礎上，考慮動態及融合特性的影響.度中心性和介數中心性是節點重要度評估中最常用的指標，分別基于網絡局部屬性和全局屬性反映單層復雜網絡中節點的重要性.但對于動態融合復雜網絡，其拓撲結構由于網絡融合而具有新的變化，因此本文結合其特性進行重新定義.此外，提出節點融合中心性指標，從節點促進網絡融合的角度反映其重要性.

定義2融合網絡節點度中心性.

融合網絡中節點vi的度中心性定義為

(2)

定義3融合網絡節點介數中心性.

融合網絡中節點vi的介數中心性定義為

(3)

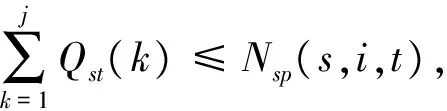
定義4融合網絡節點融合中心性.

融合網絡中節點vi的融合中心性定義為

對于融合節點，其融合中心性表示融合節點對網絡融合的貢獻程度.一旦網絡拓撲參數確定，所有融合節點的融合中心性是一個與其位置特性無關的固定值，從宏觀上反映網絡中所有融合節點對網絡融合的貢獻程度.融合節點比例越低，融合路徑比例越低，融合節點分布越密集，則網絡的融合程度越低.而在網絡融合程度低的情形下，融合節點發揮的作用就越大，從而融合節點對網絡融合的貢獻程度就越高.另外，加入參數Rncp考慮網絡動態性對融合路徑的影響，使指標的計算更加客觀.

對于非融合節點，其融合中心性表示非融合節點對網絡融合的輔助作用程度，主要體現在作為融合節點之間的中繼節點.其中，Nacn為節點vi的鄰居融合節點數量，ci為節點vi的融合聚類系數，反映其鄰居融合節點之間的連通程度，定義為

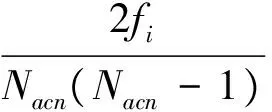
式中，fi為節點vi與其任意兩個鄰居融合節點之間所形成的三角形的個數.若gi=1或Nacn=0，則令ci=+.

由于非融合節點的融合中心性主要體現在連通那些原本相互之間連通程度較弱的融合節點上，因此節點vi的鄰居融合節點的比例越高，且它們之間的連通程度越弱，則非融合節點對網絡融合的輔助作用程度越高.如圖2所示，圖2(a)、(b)、(c)中節點1的融合中心性分別為0.40、0.60、0.36.圖2(b)比圖2(a)的值高是因為融合節點比例增加，圖2(c)比圖2(b)的值低是因為融合聚類系數提高，節點1在連通融合節點3、4、5的作用上減弱了，其融合中心性也要降低.

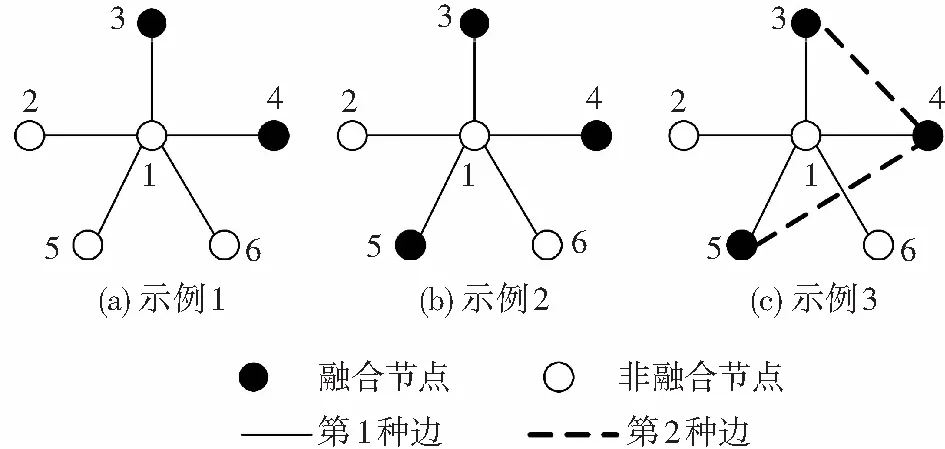
圖2 非融合節點的融合中心性示例

定義5融合網絡節點重要度.

根據定義2～定義4，綜合考慮局部位置信息、全局位置信息、網絡融合特性3個方面，定義融合網絡的節點重要度為

Ii=α×Di+β×Bi+γ×Ci.

式中，α、β、γ∈(0,1)，且α+β+γ=1，通過3個參數的設置可以調節各中心性在最終節點重要度評估中的權重.一般來說，網絡拓撲結構對節點重要度的影響是主要的，因此參數α和β應設置較大一些.融合中心性是在動態融合網絡模型中對節點重要度評估的一個改進和補充，因此參數γ應設置小一些.

3 實驗分析

3.1 典型算例

為驗證本文節點重要度評估方法的有效性，以文獻[15]中的交織風箏網絡為基礎網絡，并加入連邊的動態特性以構成動態融合復雜網絡(如圖3所示).其中，單層網絡a包含10個節點、18條邊；單層網絡b為動態網絡，包含8個節點、13條邊，邊上的數值代表邊的連通概率；融合網絡c為網絡a和b融合構成的網絡，包含13個節點、31條邊，其中5個融合節點分別由網絡a和b中具有相同編號的節點融合形成.

實驗中設置參數α=0.4，β=0.4，γ=0.2，通過MATLAB 2010a進行仿真實驗，分別計算單層網絡a和b中各節點的度中心性和介數中心性，以及網絡融合后各節點在融合網絡中的中心性指標，仿真結果見表1～3.

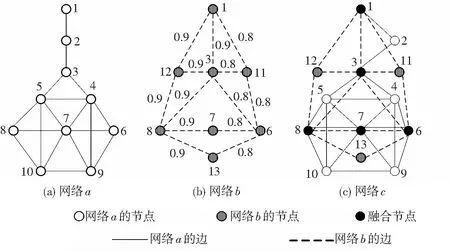
圖3 動態交織風箏網絡

節點編號12345678910111213網絡a0．1110．2220．3330．5560．5560．3330．6670．3330．4440．444———網絡b0．428—0．714——0．5710．2860．571——0．4290．4290．286網絡c(文獻[15])0．6740．1671．5860．4160．4161．4451．3491．4450．3330．3330．2310．2310．167網絡c(本文)0．4440．1671．0670．4160．4160．8750．6670．8750．3330．3330．2500．2500．167

表2 介數中心性

表3 融合中心性和節點重要度

由表1可以看出，融合節點1、3、6、7、8的度中心性較高，一是網絡融合后這些節點的度有所增加，二是式(2)使融合節點的度中心性得到加強，而非融合節點由于融合網絡節點總數的增加而使其度中心性降低，說明本文計算節點度中心性考慮了網絡融合的影響，這與文獻[15]是類似的.節點3在融合網絡中具有最高的度值并且得到加強，因而其度中心性排名最高.

由表2可以看出，本文計算的所有節點的介數中心性都不高，雖然網絡融合產生了更多的節點對和最短路徑，但式(3)考慮融合路徑和網絡動態性后使計算結果較小.與文獻[15]相比，雖然本文計算節點介數中心性的條件比較嚴格，但能夠在動態融合的網絡環境下真實反映信息傳播對介數的貢獻.節點3在各單層網絡中就具有最高的介數中心性，網絡融合后仍是許多融合最短路徑所經過的節點，因此其介數中心性排名最高.節點6和8在單層網絡中的介數中心性排名比較低，但網絡融合后在融合最短路徑上的貢獻度較大，因此介數中心性排名比較靠前.同時，節點8比節點6的值稍高，是因為網絡b左半部分的邊連通概率比右半部分的高，這點在其他對稱的節點對(如節點4、5、9和10、11和12)之間也有所體現，從而說明本文的指標能夠反映網絡連通性的影響.節點1的介數中心性不再是單層網絡中的0，主要是網絡融合后該節點在融合最短路徑上有所貢獻.節點2的介數中心性由網絡a中的0.222變為0，是由于節點1和3之間的連邊使節點2的兩條鄰邊成為了冗余路徑.

如表3所示，融合中心性方面，融合節點的值為0.429，是融合節點比例、融合路徑比例和融合節點分布等3個網絡融合參數共同決定的，反映了融合節點對網絡融合的貢獻程度.非融合節點2、11、12、13的融合中心性較高，說明它們在輔助網絡融合方面起到了較大作用，從網絡拓撲中也可以看出它們都是連接融合節點的樞紐，在融合程度不高的網絡中它們的重要性更是不能忽視.節點重要度方面，本文綜合考慮網絡拓撲結構和動態融合特性等因素，對節點重要度的評估是一個綜合評價指標.5個融合節點的重要度位居前列，這也與指標設計的基本思想是一致的.對稱節點對的重要度差異主要來自介數中心性的計算，最終反映了網絡動態性對節點重要度的影響.非融合節點13的排名緊跟融合節點之后，主要在于其融合中心性的作用，體現了對非融合節點重要度的加強，使節點重要度評估更加全面、客觀.

在節點重要度評估中，節點度中心性和融合中心性主要考慮網絡融合性的影響，節點介數中心性主要考慮網絡動態性的影響，并通過α、β、γ這3個參數的設置進行調節.由于節點度中心性和介數中心性是以網絡拓撲結構為基礎，而網絡拓撲結構是節點重要度的主要影響因素，因此本文給參數γ一個較小的固定值，并考察參數α和β的不同變化對節點重要度的影響，仿真結果如圖4所示.可以看出，隨著α的增大，網絡融合性的影響增強，融合節點的重要度有顯著的提高.隨著β的增大，網絡動態性的影響增強，各節點的重要度均有所降低，尤其對節點9～12等介數中心性較小的節點影響較大，β=0.2時其重要度均排在節點13之前，而β=0.8時均排在節點13之后.

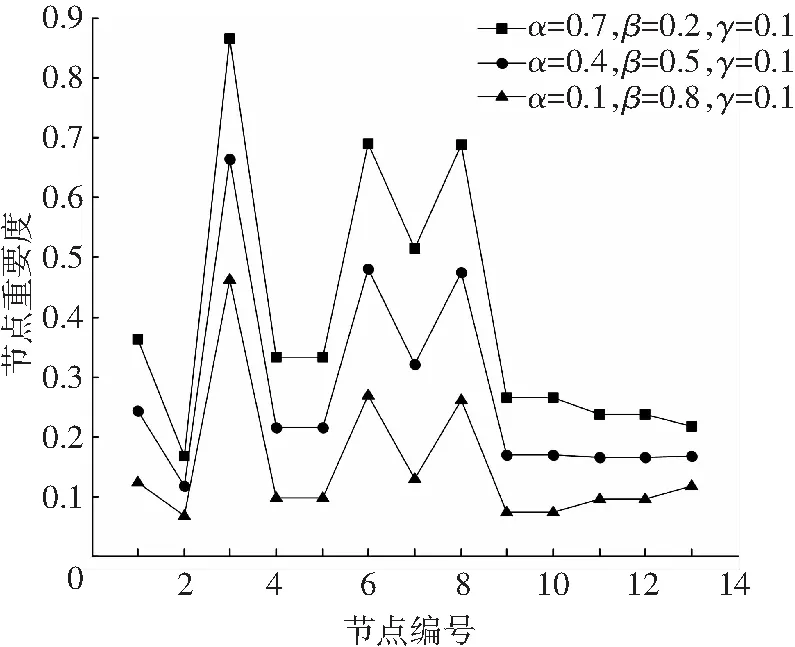
圖4 不同參數設置下的節點重要度

3.2 仿真網絡

為進一步驗證本文方法的適用性，利用NS2搭建仿真網絡，仿真場景及其對應的網絡拓撲如圖5、6所示.該仿真網絡由光通信網和衛星通信網融合構成，是典型的有線與無線混合組網的情景.網絡中共有15個節點，其中有線節點7個(W1～W7)，無線節點5個(M1～M4，B1)，融合節點3個(B2～B4).網絡中共18條鏈路，其中有線鏈路11條，無線鏈路7條.另外，仿真網絡中僅反映無線節點之間的連通關系(即兩個無線節點之間是否存在無線鏈路)，而不考慮其運動情況.

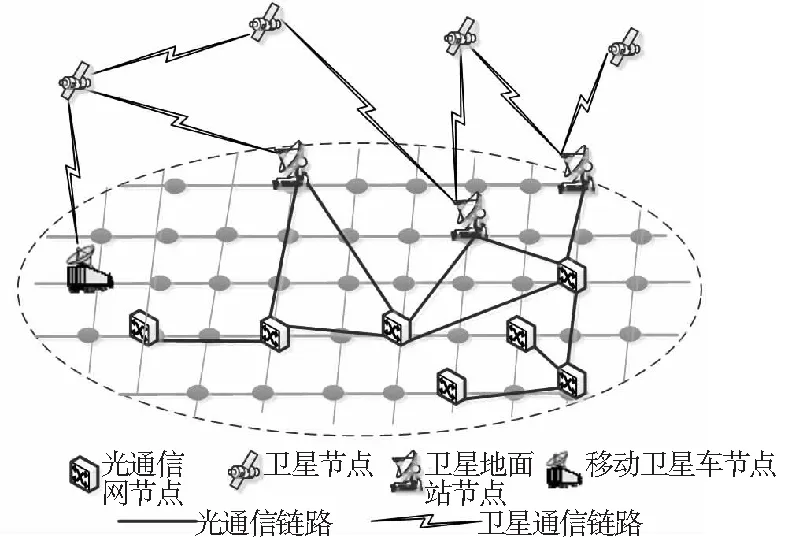
圖5 仿真場景

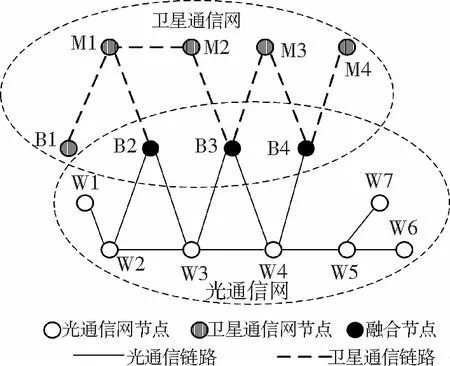
圖6 網絡拓撲

鏈路連通率反映了鏈路兩端點之間成功發送或接收數據的情況，因此本文采用鏈路連通率計算無線鏈路的邊連通概率.設置背景流量模擬網絡中的數據傳輸情況，通過流量發生器的源/目的節點設置使數據流覆蓋所有鏈路.仿真時間共100 s，以1 s為時間間隔測量無線鏈路的連通率，并取仿真時間內測量所得的鏈路連通率的平均值作為該無線鏈路的邊連通概率，計算結果見表4.設置參數α=0.4，β=0.4，γ=0.2，計算節點的度中心性、介數中心性、融合中心性和節點重要度，見表5.

表4 邊連通概率

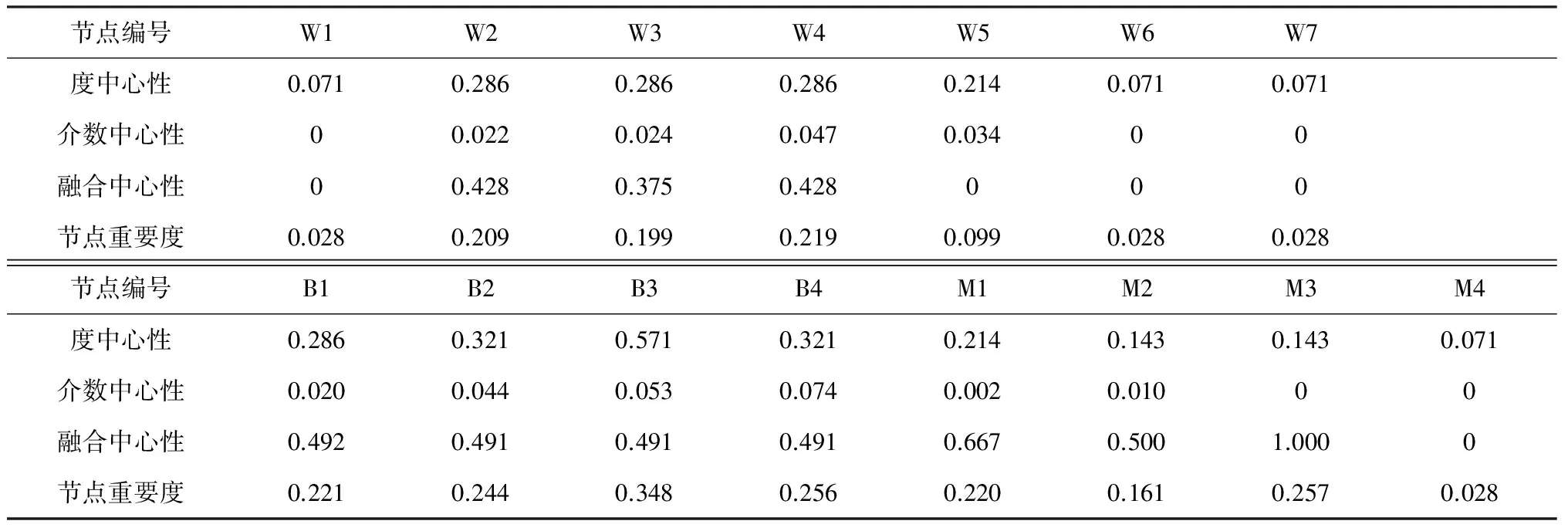
表5 中心性指標及節點重要度

由表5可以看出，B2～B4等3個融合節點的度中心性和介數中心性相對其他非融合節點較高，反映了在動態融合網絡環境中融合節點在拓撲結構上的重要性，而對于W1、W6、W7、M4等處于網絡邊緣的節點，其度中心性和介數中心性均較低.3個融合節點的融合中心性為0.491，而M1～M3等3個非融合節點的融合中心性較高，反映出它們對網絡融合的輔助作用程度較大.綜合3個中心性指標計算得出，3個融合節點的重要度較高，M3節點由于其融合中心性高而使其重要度也較高，W1、W6、W7、M4等節點由于各中心性指標均較低而使其重要度較低，其他節點的重要度處于中間的位置.通過上述分析，利用本文方法基本能夠合理地反映不同節點在動態融合網絡中的重要程度，進一步驗證了在仿真網絡環境中本文方法的有效性.

4 結 論

1)針對有/無線多網融合的層級網絡，本文綜合考慮網絡拓撲結構、動態融合特性等因素，提出了動態融合復雜網絡模型及其節點重要度評估方法.以改進的動態交織風箏網絡和NS2搭建的仿真實驗網絡為例進行仿真分析，結果表明，該方法能夠比較全面地反映動態融合復雜網絡中節點的重要度.

2)本文定義的動態網絡僅限于邊的連通性變化，未考慮節點數量的增減[19]，下一步可采用大規模有/無線融合通信網等真實網絡進行驗證.

3)文中節點重要度的計算采用各中心性指標線性加權得出，參數設置比較簡單，未來可考慮采用多屬性決策[20]等方法作進一步研究.

[1] WATTS D J, STROGATZ S H. Collective dynamics of small-world networks[J]. Nature, 1998,393(6684): 440-442. DOI: 10.1038/30918.

[2] BARABASI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439):509-512. DOI: 10.1126/science.286.5439.509.

[3] 紐曼. 網絡科學引論[M]. 郭世澤, 陳哲, 譯. 北京: 電子工業出版社, 2014: 106.

NEWMAN M E J. Networks: an introduction[M]. Guo S Z, Chen Z. Beijing: Publishng House of Electronics Industry, 2014: 106.

[4] 周濤, 張子柯, 陳關榮, 等. 復雜網絡研究的機遇與挑戰[J]. 電子科技大學學報, 2014,43(1):1-5.DOI: 10.3969/j.issn.1001-0548.2014.01.001.

ZHOU Tao, ZHANG Zike, CHEN Guanrong, et al. The opportunities and challenges of complex networks research[J]. Journal of University of Electronic Science and Technology of China, 2014, 43(1):1-5. DOI: 10.3969/j.issn.1001-0548.2014.01.001.

[5] 劉建國, 任卓明, 郭強, 等. 復雜網絡中節點重要性排序的研究進展[J]. 物理學報, 2013, 62(17):178901. DOI:10.7498/aps.62.178901.

LIU Jianguo, REN Zhuoming, GUO Qiang, et al. Node importance ranking of complex networks[J]. Acta Physica Sinica, 2013, 62(17):178901. DOI:10.7498/aps.62.178901.

[6] KOURTELLIS N, ALAHAKOON T, SIMHA R, et al. Identifying high betweenness centrality nodes in large social networks[J]. Social Network Analysis and Mining, 2013, 3(4):899-914. DOI: 10.1007/s13278-012-0076-6.

[8] SAITO K, KIMURA M, OHARA K, et al. Efficient discovery of influential nodes for SIS models in social networks[J]. Knowledge and Information Systems, 2012, 30(3): 613-635. DOI: 10.1007/s10115-011-0396-2.

[9] ZHOU Jingyu, ZHANG Yunlong, CHENG Jia. Preference-based mining of top-K influential nodes in social network[J]. Future Generation Computer Systems, 2014, 31:40-47. DOI: 10.1016/j.future.2012.06.011.

[10]張欣. 多層復雜網絡理論研究進展：概念、理論和數據[J]. 復雜系統與復雜性科學, 2015, 12(2):103-107. DOI: 10.13306/j.1672-3813.2015.02.016.

ZHANG Xin. Multilayer networks science: concepts, theories and data[J]. Complex Systems and Complexity Science, 2015, 12(2):103-107. DOI: 10.13306/j.1672-3813.2015.02.016.

[11]BULDYREV S V, PARSHANI R, PAUL G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010(464):1025-1028.DOI: 10.1038/nature08932.

[12]陳宏斌, 樊瑛, 方錦清, 等. 二元隨機網[J]. 物理學報, 2009, 58(3):1383-1390.

CHEN Hongbin, FAN Ying, FANG Jinqing, et al. Bielemental random networks[J]. Acta Physica Sinica, 2009, 58(3):1383-1390.

[13]邵峰晶, 孫仁誠, 李淑靜, 等. 多子網復合復雜網絡及其運算研究[J]. 復雜系統與復雜性科學, 2012, 9(4):20-25.

SHAO Fengjing, SUN Rencheng, LI Shujing, et al. Research of multi-subnet composited complex network and its operation[J]. Complex Systems and Complexity Science, 2012, 9(4):20-25.

[14]郭進利, 祝昕昀. 超網絡中標度律的涌現[J]. 物理學報, 2014, 63(9):090207. DOI:10.7498/aps.63.090207.

GUO Jinli, ZHU Xinyun. Emergence of scaling in hypernetworks[J]. Acta Physica Sinica, 2014, 63(9):090207. DOI:10.7498/aps.63.090207.

[15]沈迪, 李建華, 張強, 等. 交織型層級復雜網[J]. 物理學報, 2014, 63(19):190201. DOI:10.7498/aps.63.190201.

SHEN Di, LI Jianhua, ZHANG Qiang, et al. Interlacing layered complex networks[J]. Acta Physica Sinica, 2014, 63(19):190201. DOI:10.7498/aps.63.190201.

[16]HOLME P, SARAMAKI J. Temporal networks[J]. Physics Reports, 2012,519(3):97-125. DOI:10.1016/j.physrep.2012.03.001.

[17]BASARAS P, KATSAROS D, TASSIULAS L. Detecting influential spreaders in complex, dynamic networks[J]. Computer, 2013,46(4):24-29. DOI: 10.1109/MC.2013.75.

[18]MASAKI O. A method for extracting influential nodes while considering the development of social networks[C]// Proceedings of the 2012 Second International Conference on Cloud and Green Computing. Xiangtan, China: IEEE, 2012: 456-459. DOI: 10.1109/CGC.2012.77.

[19]ZHOU Jian, PAN Jiaxin, ZHOU Yanran. Node importance evaluation based on network heterogeneity[C]// Proceedings of the 2010 International Conference on Communications and Mobile Computing. Shenzhen, China: IEEE, 2010:188-194. DOI: 10.1109/CMC.2010.112.

[20]于會, 劉尊, 李勇軍. 基于多屬性決策的復雜網絡節點重要性綜合評價方法[J]. 物理學報, 2013, 62(2): 020204. DOI:10.7498/aps.62.020204.

YU Hui, LIU Zun, LI Yongjun. Key nodes in complex networks identified by multi-attribute decision-making method[J]. Acta Physica Sinica, 2013, 62(2): 020204. DOI:10.7498/aps.62.020204.

Nodeimportanceevaluationindynamicconvergencecomplexnetworks

FU Kai1,2， XIA Jingbo3， ZHAO Xiaohuan4

(1.Information and Navigation College, Air Force Engineering University, Xi’an 710077, China; 2.Unit 95246, Nanning 530003, China; 3.Tan Kah Kee College, Xiamen University, Zhangzhou 363105, Fujian, China; 4.Unit 95340, Baise 533616, Guangxi, China)

To seek key nodes and improve network robustness, the dynamic convergence complex network model and its node importance evaluation method are proposed for wired and wireless integrating layered networks. Considering characteristic of dynamic convergence complex networks, parameters including edge connection probability, path connection probability, network connection probability, convergence node proportion, convergence node distribution and convergence path proportion are designed. Based on node importance evaluation indexes in single-layer complex networks, the node degree centrality, node betweenness centrality and node convergence centrality in dynamic convergence complex networks are presented. Node convergence centrality of convergence nodes indicates their contribution to network convergence, and that of non-convergence nodes indicates their auxiliary effect to network convergence, especially they are used as relay nodes among convergence nodes. At last, node importance evaluation is implemented considering network topology structure and its dynamic convergence characteristic. Typical example results of improved dynamic convergence kite networks show that the proposed method can comprehensively depict the node importance in dynamic convergence complex networks. Simulation network composed of fiber communication network and satellite communication network is designed by NS2, further indicating the effectiveness of the proposed method.

complex networks; dynamic convergence; node importance; degree centrality; betweenness centrality; convergence centrality

10.11918/j.issn.0367-6234.201607012

TP393

A

0367-6234(2017)10-0112-08

2016-07-05

航空科學基金(20141996018)；陜西省自然科學基礎研究計劃項目(2012JZ8005)

付 凱(1987—)，男，博士研究生；

夏靖波(1963—)，男，教授，博士生導師

付 凱，fukaia3@163.com

(編輯張 紅)