不同速比下縱搖運動對立軸葉輪的性能影響

王 凱，孫 科,張 亮

(哈爾濱工程大學 深海工程技術研究中心，哈爾濱 150001)

不同速比下縱搖運動對立軸葉輪的性能影響

王 凱，孫 科,張 亮

(哈爾濱工程大學 深海工程技術研究中心，哈爾濱 150001)

浮式立軸水輪機在波浪中會發生縱搖運動，為了研究縱搖對立軸水輪機的水動力性能影響，將浮式垂直軸葉輪在波浪作用下搖蕩運動的復雜模型簡化為葉輪在均勻流中疊加簡諧搖蕩運動，應用ANSYS-CFX軟件，采用動網格和滑移網格相結合的技術建立了垂直軸葉輪旋轉和搖蕩運動的數值模擬方法,并和在均勻流中的水輪機作對比，而且對水輪機的推力系數和側向力系數的時歷曲線用最小二乘法進行擬合分析，得到水輪機阻尼系數和附加質量系數.結果表明：縱搖運動下的水輪機效率會稍微高于均勻流中的水輪機效率；縱搖運動下的水輪機推力和側向力波動幅值有大幅增加，對水輪機結構強度及疲勞效應產生不利影響；阻尼力是水輪機縱搖運動中的主要成分，附加質量力占的影響較小.

立軸水輪機；縱搖運動；阻尼系數；附加質量系數；水動力性能；最小二乘法

當今社會，化石能源在能源比例中仍然占據很大比例，但其可開采量越來越少.所以，世界上很多國家已經開始重視對綠色可再生能源的開發研究，同時潮流能也因為它的可持續性、高密度和可預測性的特點，正逐漸引起人們的重視[1-4].

潮流能水輪機是主要的潮流能開發裝置，根據主軸和來流方向的關系可以分為水平軸和垂直軸(立軸)兩種[5].在較深的海況中，浮式平臺是水輪機最好的載體，因為浮式平臺不僅可以作為水輪機、發電機及其他設備的載體，而且浮式平臺的維護、拆卸和安裝更加便利[6].但是浮式平臺在波浪的作用下會發生6個自由度的搖蕩運動，這種工況會對水輪機水動力性能有很大影響.

浮式海洋結構物在波浪作用下的水動力系數變化一直是研究者關注的重點，但是大多數海洋浮式結構都有著復雜的外形以至于對它們水動力性能的研究存在很大阻力，所以早期學者最開始都是用最簡單的結構來研究波浪下的水動力問題，如圓柱體和球體.Yeung[7]選取有限水深下的圓柱體來研究其水動力性能，通過匹配其內部和外部問題的特征函數來研究圓柱的升沉、搖蕩和翻滾3類輻射問題，然后給出了圓柱的阻尼系數和附加質量系數.結果表明,升沉附加質量是對數奇異的，而且在低頻時阻尼系數趨近一個常數.Lopes等[8]研究了半潛式球體的脈動運動形式下的水動力性能，結果表明在接近共振頻率時，振蕩形式下的阻尼系數和附加質量系數比升沉、搖擺形式下的系數要高，而且水深對阻尼系數的影響僅限于低頻范圍內.另外很多研究人員利用多級方法、特征函數法或者其他方法對簡單的結構物(圓柱、球)在波浪下的水動力性能做了詳細的研究[9-11].

但是真正的海洋結構物有著復雜的外形，按照上述方法對它們在波浪中的水動力性能問題的求解存在很大困難.因此CFD方法和實驗方法成為研究波浪中復雜外形的海洋結構物水動力性能的主要方法.Pavon等[12]利用實驗和CFD方法對比分析半潛式浮式風機垂蕩板的水動力系數，實驗模型直徑為1 m，是已知最大的實驗模型.實驗測量了阻尼系數和附加質量系數，并和CFD的計算結果對比，為浮式風機的概念設計提供參考標準.2010年，Galloway等[13]研究了三葉片水平軸水輪機在波浪中的性能影響，發現推力波動最大增加了37%、力矩增加35%；2013年， Lust等[14-15]做了相似實驗發現波浪中葉輪性能波動現象明顯，但這些研究也僅限于水平軸水輪機.

到目前為止，對浮式立軸水輪在波浪中水動力性能影響還處于探索階段.本文利用CFD技術研究立軸水輪機發生強迫縱搖運動情況下的水動力性能變化情況，針對不同速比下的水輪機工況，并和均勻流中的水輪機水動力性能對比，找出縱搖對水輪機水動力的影響規律；并采用最小二乘法原理[16]擬合縱搖水輪機的推力和側向力系數時歷曲線，得到波浪中的水輪機阻尼系數及附加質量系數.

1 數值模擬

1.1 理論基礎

垂直軸葉輪來流方向為X軸正向，表1 為立軸潮流能水輪機的主要參數.

為了方便分析，定義量綱一的參數如下：

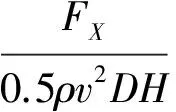
表1 立軸水輪機參數

阻尼項和附加質量項是葉輪位置角θ的函數，將它們可以展開三角級數形式為：

最后推力系數可以寫成下列級數形式：

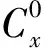
(1)

側向力系數可以寫成下列級數形式：

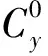
(2)

利用CFD 方法模擬立軸水輪機在波浪中的縱搖運動，可以得到CFX和CFY的時歷曲線，然后用最小二乘法擬合可以得到均勻水動力項、阻尼項和附加質量項.

1.2 立軸水輪機模型

立軸水輪機的試驗研究一般是在循環水槽中進行的，水輪機被安在實驗平臺上，水輪機在水流沖擊下轉動，并通過設定循環水槽中水流流速來模擬不同的海流情況，實驗總布置圖如圖1(a)所示.試驗平臺具體布置如圖1(b)所示，傳動軸、齒輪、傳感器、發電機和剎車電機等依次安裝在實驗平臺上.傳動軸與一傘形齒輪相連，傘形齒輪通過蝸桿連接到轉矩轉速傳感器，傳動軸上方還裝有一個小型刷環引電器；平臺下方有一法蘭盤，用于與水輪機模型相連，通過該實驗平臺可以測量出水輪機的效率等.哈爾濱工程大學循環水槽實驗室對立軸水輪機做了一系列實驗研究，實驗段尺度：長×寬×深為(8.0 m×1.7 m×1.5 m)，工作流速：0.2～2.0 m/s, 如圖1(c)所示.實驗所采用的水輪機模型參數為：v=1 m/s，D=0.8 m，H=0.6 m，C=0.12 m，Z=2，葉片翼型為NACA0018，實驗模型如圖1(d)所示.

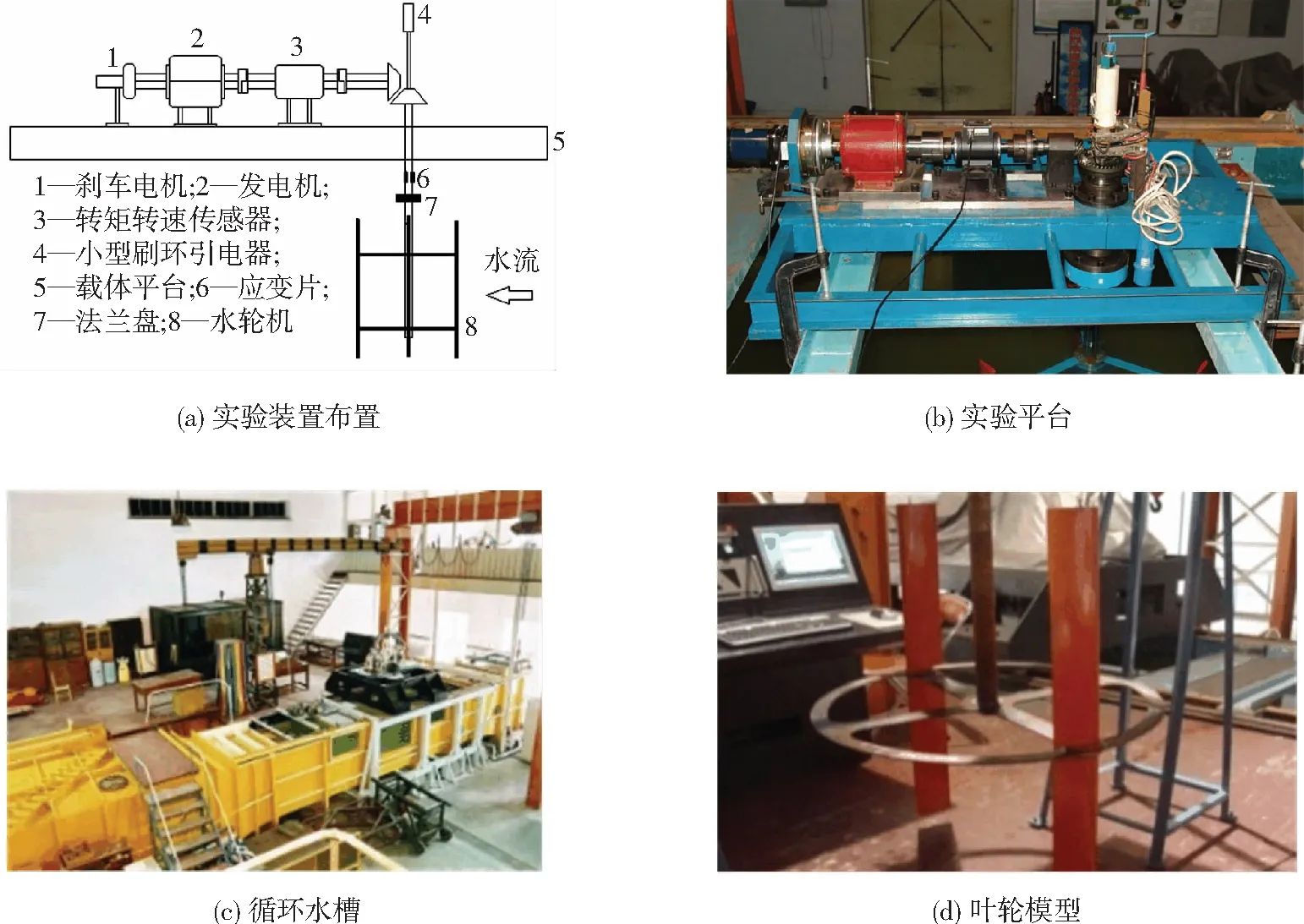
圖1 立軸水輪機實驗

除了實驗方法來研究立軸水輪機的水動力性能外，CFD方法研究水輪機的最大優勢在于可以獲得更多的流場瞬時信息，計算機的快速發展也推動著計算流體力學的發展.本文采用CFD方法模擬相同參數的水輪機來研究其水動力性能，并和實驗結果對比分析，證明CFD方法對立軸水輪機研究的可行性.如圖2為CFD計算網格模型，葉輪旋轉中心距離縱搖中心0.3 m(0.5H)，本文模擬立軸水輪機運動情況需要同時模擬葉輪的旋轉運動和縱搖運動(ξ=Asin(ωZt))，所以將計算網格分為旋轉域、縱搖域和外域3部分，如圖2(b)、(c)、(d)所示，各個域之間的相對運動都是旋轉運動，且3個域之間采用滑移網格形式.

整個計算域網格都采用結構化網格，邊界條件設置如下：模型的入口邊界為速度入口；出口邊界為壓力出口，相對壓力為0；外域的側面邊界和葉片表面分別為自由滑移壁面和無滑移壁面條件；旋轉域和縱搖域分別給定旋轉角速度和縱搖簡諧運動；計算選取的湍流模型為SST模型，選擇瞬態求解器，時間步長為葉輪自轉1°所使用的時間，時間步長的選取文獻[5,7]的研究方法.

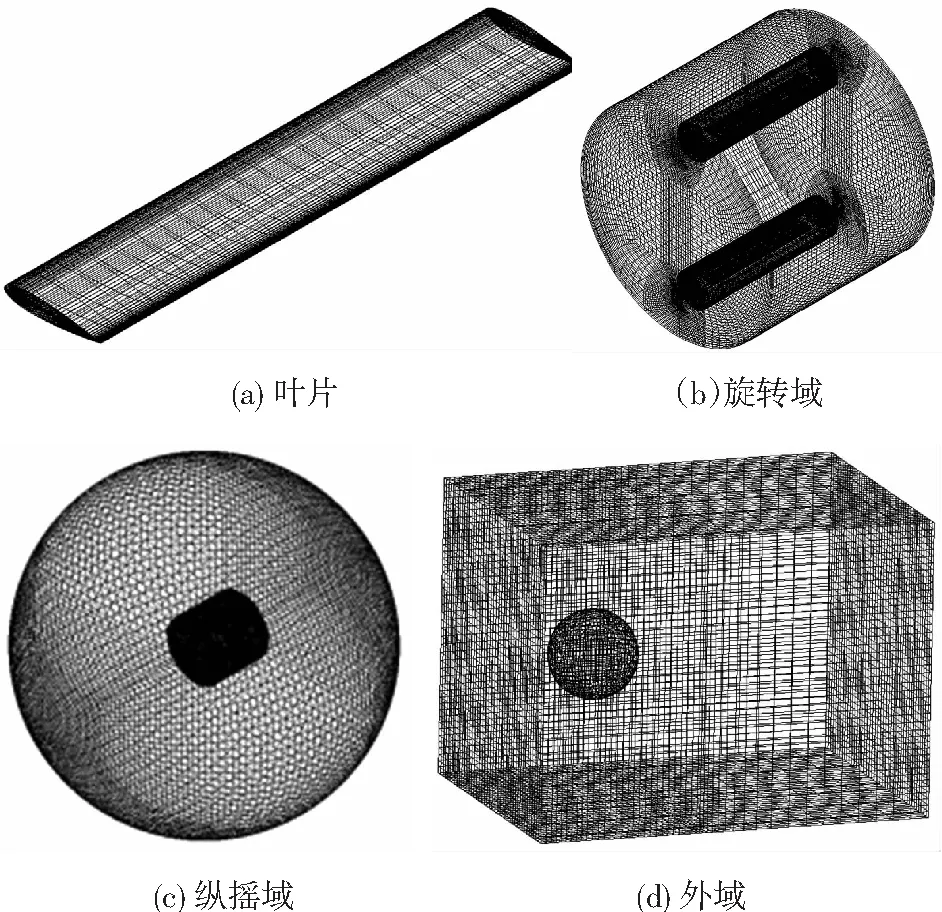
圖2 網格模型

2 結果與分析

2.1 CFD方法的可行性證明

在來流速度v=1 m/s，葉輪不發生縱搖的工況下比較同一個水輪機在實驗方法和CFD方法得出的效率—速比對比如圖3所示.從圖3中可以看出速比2.5時，兩種方法的水輪機效率都達到峰值，不同速比下的效率都比較接近，微小的差異可能是由于實驗設備限制、自由液面等造成的，但這一結果對比證明了CFD方法在立軸水輪機水動力性能研究方面的可行性.

2.2 縱搖對立軸水輪機效率的影響

來流速度v=1 m/s，分別模擬均勻流中不發生搖蕩的工況和波浪中發生縱搖運動.假設水輪機的縱搖頻率在常見的波浪頻率范圍內，規定縱搖頻率為1.2 rad/s.測量兩種運動工況下不同速比時的水動力性能.

如圖4為縱搖工況下和非縱搖工況下的水輪機效率-速比對比圖.從圖4中看出縱搖對水輪機效率曲線趨勢沒有大的影響，都是在速比2.5左右效率達到峰值.縱搖工況下的效率值略大于非縱搖的值，特別在峰值處更加明顯.

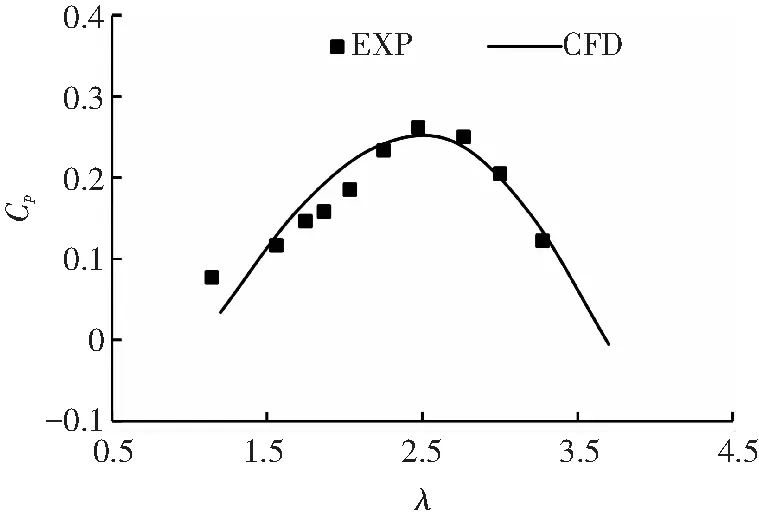
圖3 實驗結果和CFD結果比較

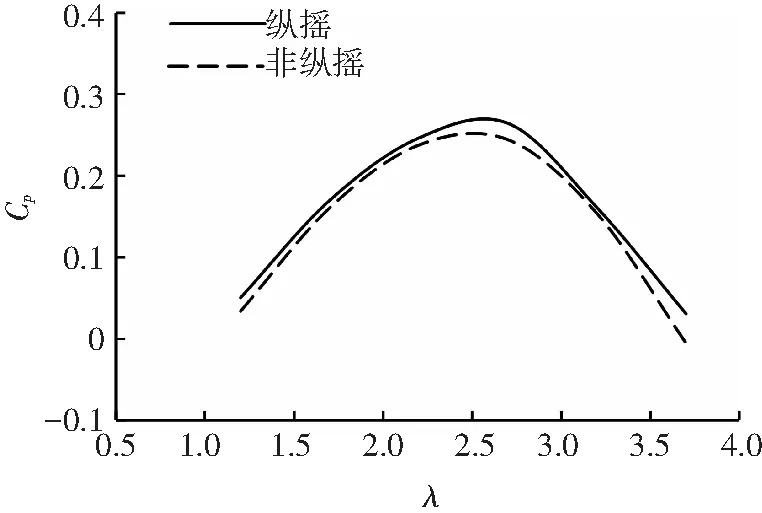
圖4 立軸水輪機能量利用率曲線對比

Fig.4 Comparison of energy utilization coefficients under different conditions

從圖5(a)可以看出，非縱搖水輪機的尾渦幾乎是對稱分布的，圖5(b)、(c)是縱搖時兩個不同狀態下的水輪機尾渦場.

圖5 水輪機尾渦場比較

從圖中可以看出水輪機尾渦受到縱搖的影響，和非縱搖尾渦場有明顯差別.在縱搖情況下，葉片周圍水流場會受到縱搖的影響，縱搖工況誘導的速度和自身旋轉的速度相互影響使葉片周圍流場復雜化，從而引起葉片受力增大，切向力的增大會引起葉輪效率提高.

2.3 縱搖對水輪機推力側向力的影響

水輪機的推力和側向力是影響水輪機結構強度和水動力性能的重要參數，通過對比在均勻流中不發生縱搖的立軸水輪機和波浪中發生縱搖情況下的水輪機的推力和側向力曲線(λ=1.5)，為水輪機的設計提供參考.

如圖6(a)、(b)所示，在均勻流中的立軸水輪機的推力和側向力是按照其自身旋轉頻率規則波動，兩條時歷曲線波峰和波谷的極值幾乎不變.在波浪中發生縱搖運動的水輪機推力和側向力的波動既受到自身旋轉頻率的影響，又受葉輪縱搖頻率的影響.如圖6(c)、(d)所示，縱搖工況下的葉輪推力和側向力的上下包絡線明顯有很大波動.

為了對比分析縱搖運動不同速比下的水輪機推力和側向力波動規律，分別選取速比λ=1.0、1.5、2.0、2.5、3.0，比較它們的推力側向力包絡曲線，如圖7所示.

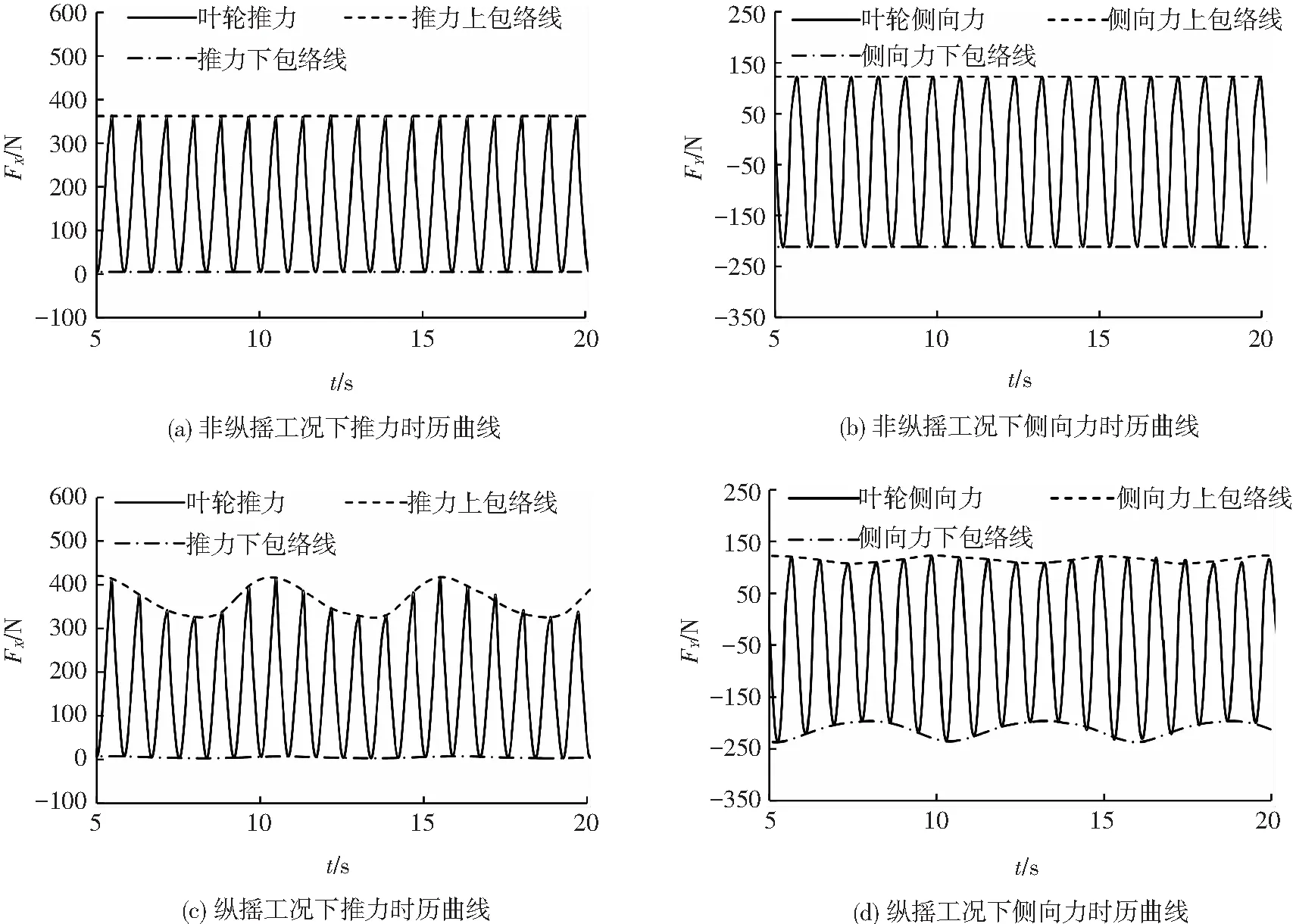
圖6 縱搖和非縱搖工況的受力時歷曲線

如圖7(a)、(b)為不同速比時的水輪機推力的上、下包絡線時歷曲線對比圖.圖7(c)、(d)為不同速比時的水輪機側向力的上、下包絡線時歷曲線對比圖.當水輪機在均勻流中不發生縱搖運動時，水輪機的推力和側向力的包絡線都為直線形式.從4幅圖中可以看出水輪機發生縱搖運動時，推力和側向力的包絡曲線明顯發生波動，而且波動形式相似.隨著速比增加，上包絡線的值隨著增大，而下包絡線正好相反，隨著速比增大而減小.推力和側向力在縱搖情況下的波動對水輪機的結構強度和疲勞效應都有不利影響.

如圖8為立軸水輪機在均勻流的推力、側向力和波浪中縱搖運動的推力、側向力的波動幅值在不同速比下的對比曲線.圖8中可以看出各個力隨速比的變化規律相同，都是隨著速比增大波動幅值也隨之增大，但縱搖運動時兩個力的波動幅值比均勻流的明顯要大.例如在速比3.0時，縱搖運動下的推力波動幅值比均勻流的增大18%，側向力波動幅值則增大了將近30%，這是因為水輪機在波浪中發生縱搖運動時，葉片附近的水流受縱搖影響變得復雜，此處水流的合速度增大，從而增大了葉輪受力，這樣不利于電能的穩定輸出及水輪機的結構安全.

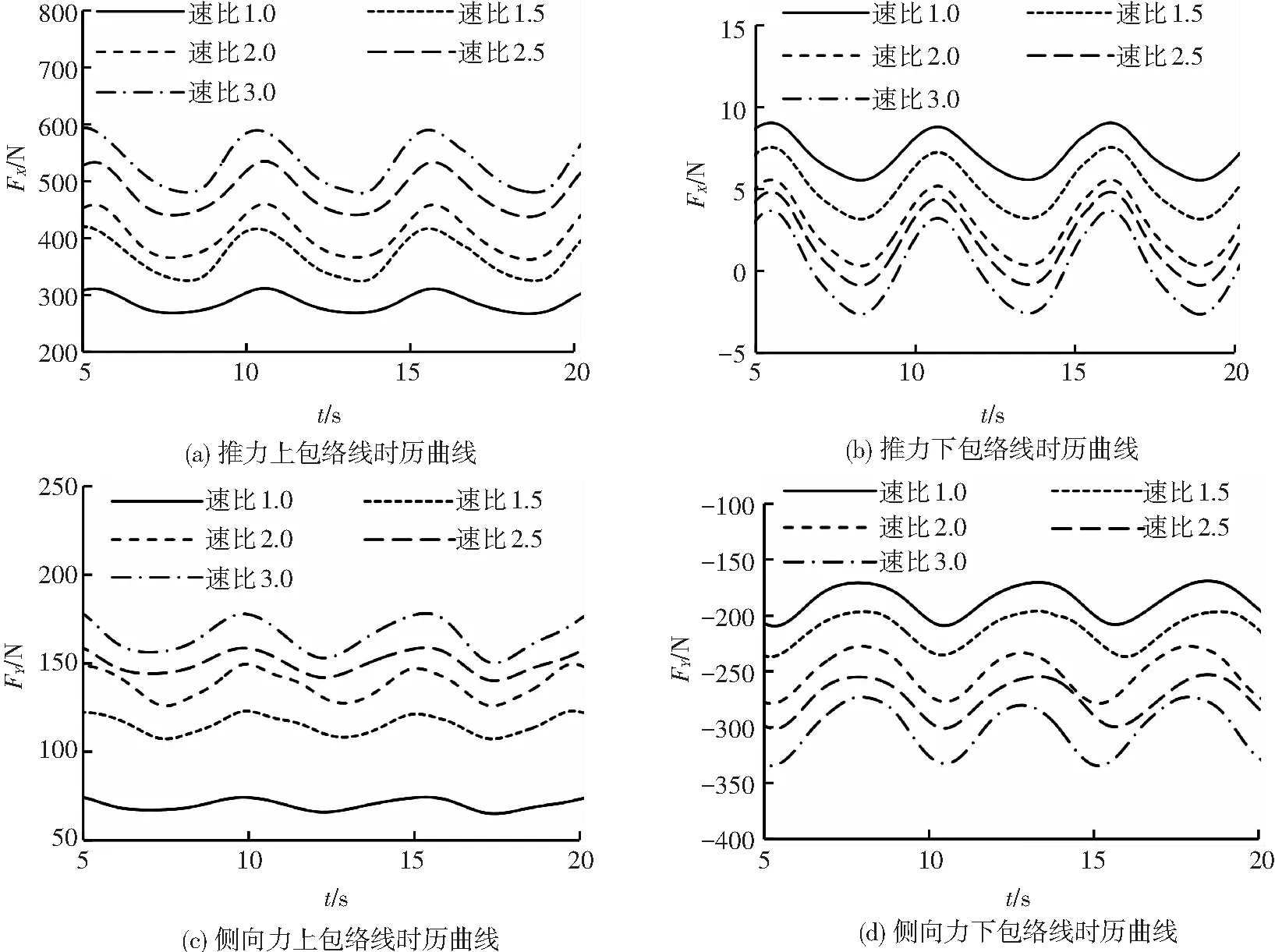
圖7 縱搖運動的推力和側向力包絡線對比

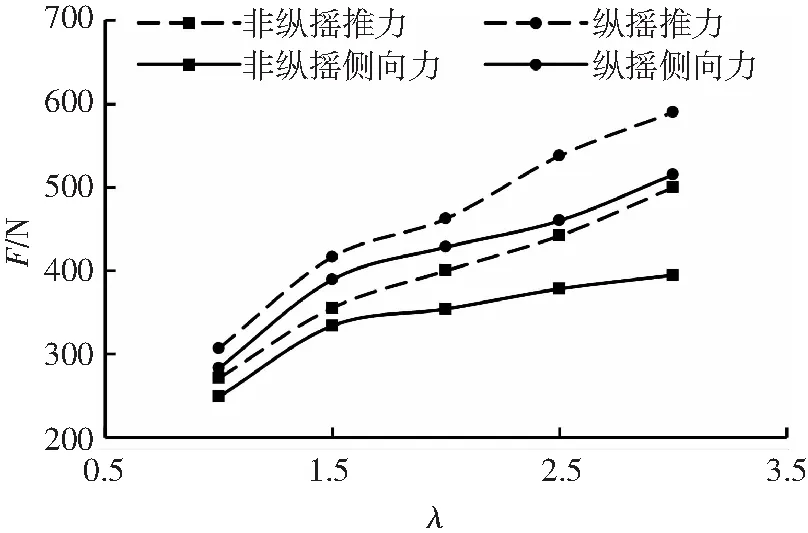
圖8 不同速比下力的波動幅值對比

Fig.8 Comparison of stress fluctuation amplitude under different speed ratio

3 載荷系數擬合分析

3.1 縱搖運動下推力系數及側向力系數的擬合

縱搖運動下的水輪機推力和側向力的時歷曲線可以通過CFD方法得到，利用最小二乘法根據式(1)、(2)可以擬合得到推力和側向力的阻尼項和附加質量項，圖9為推力和側向力的時歷曲線和擬合值的對比圖，從圖9中可以看出擬合值和被擬合的曲線高度吻合，可以對其進行對比分析.

對不同速比下推力和側向力的時歷曲線進行最小二乘法擬合，歸一化后得出CFX和CFY級數形式的各項系數，見表2、3，表中給出了CFX和CFY展開各項系數中的常數項和一次項，對其進行對比分析.

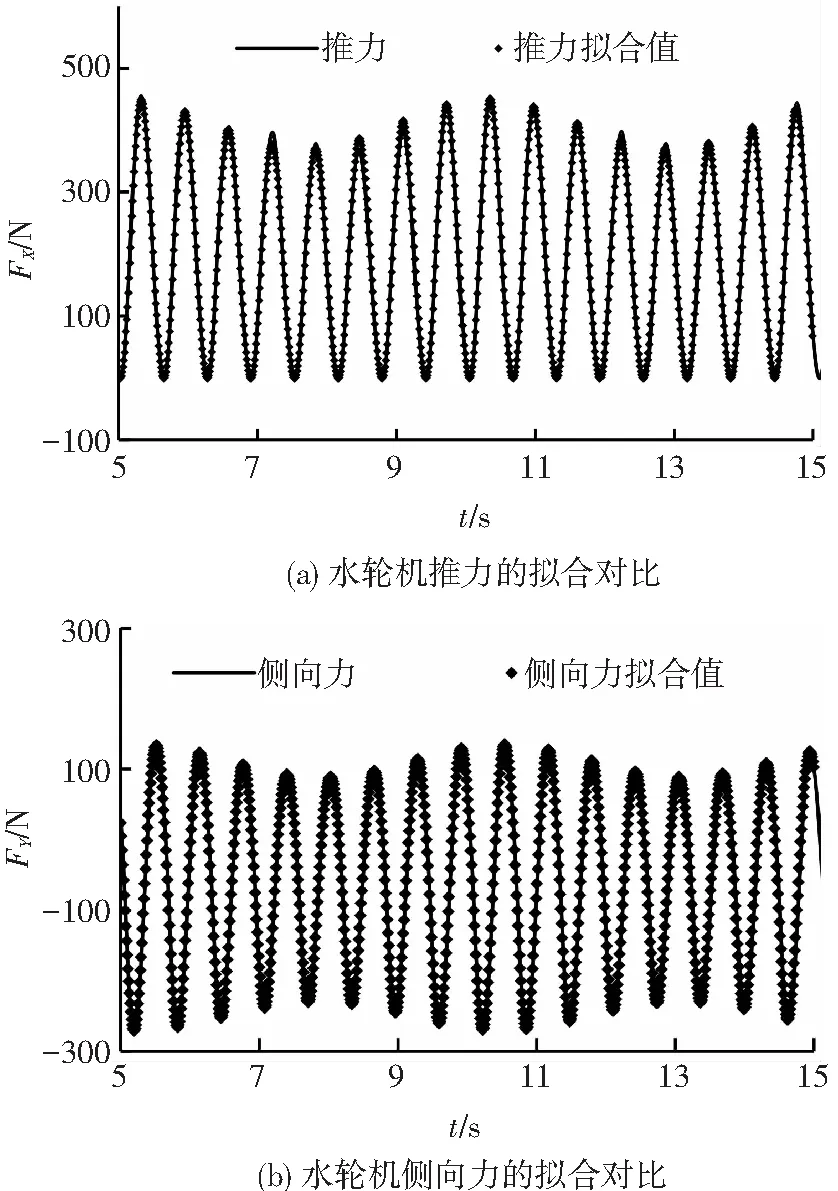
圖9 擬合值和CFD計算值的對比

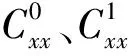
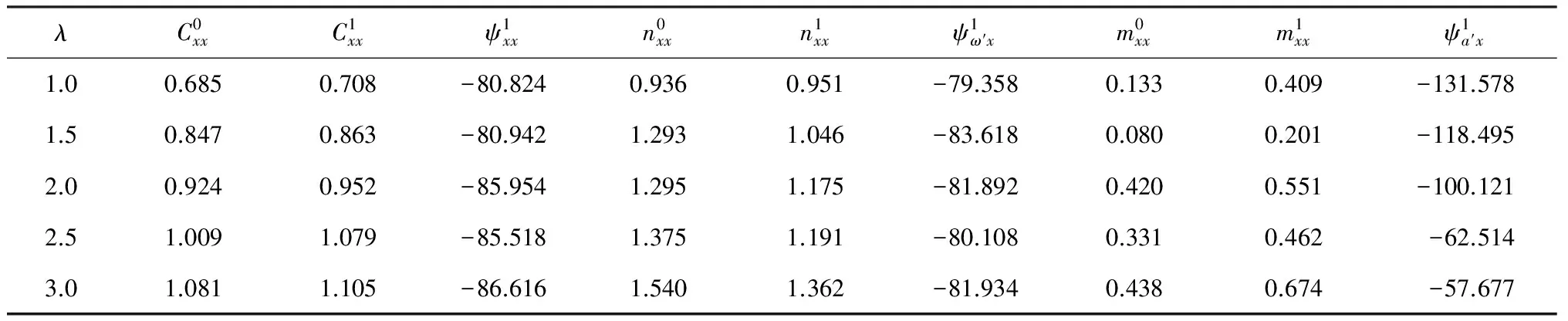
表2 CFX展開系數

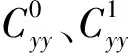
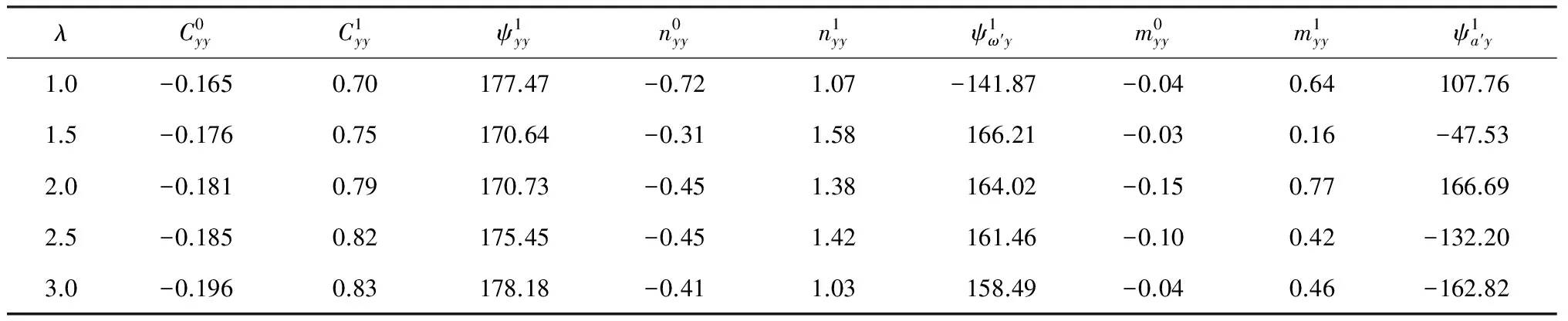
表3 CFY展開系數

3.2 水輪機計算結果的應用

本文研究了速比從1.0～3.0的強迫縱搖運動下水輪機推力和側向力，并通過最小二乘法擬合得出了附加質量和阻尼項隨速比的變化情況.因此通過插值計算，在任一速比下的縱搖水輪機的推力和側向力的附加質量和阻尼項都可以得到.然后將得到的附加質量和阻尼系數應用到浮式平臺上來分析不同速比下縱搖運動對浮式潮流電站的運動響應.

圖10為浮式垂直軸潮流電站的運動響應研究流程圖，本文主要研究的是第1步垂直軸潮流能水輪機的水動力系數分析.通過CFD方法得到不同速比強迫縱搖運動下的水動力系數時歷曲線，然后最小二乘法擬合分析得到附加質量和阻尼系數.

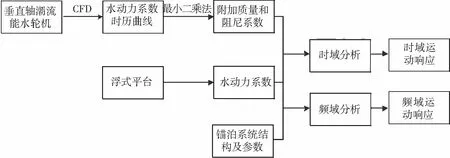
圖10 浮式垂直軸潮流能電站研究方法流程

4 結 論

1)強迫縱搖運動的立軸水輪機和均勻流中水輪機的效率曲線變化規律相似，都是在速比2.5左右達到峰值，而且縱搖情況下效率值略大于均勻流中，在速比2.5時尤其明顯.

2)隨著速比增加，推力和側向力上包絡線的值隨之增加，而下包絡線正好相反，隨著速比增加而減小.

3)立軸水輪機發生縱搖運動時，推力和側向力的波動幅值明顯比均勻流中的要大，這對葉輪的結構強度和疲勞壽命都會產生不利影響.

4)立軸葉輪的推力和側向力系數通過最小二乘法分析得到縱搖運動下的阻尼項和附加質量項，其中阻尼項比附加質量項大，所以阻尼力是水輪機縱搖運動中的主要成分，附加質量力占的影響較小.

[1] WANG Shujie, YUAN Peng, LI Dong, et al. An overview of ocean renewable energy in china[J]. Renewable and Sustainable Energy Reviews, 2011, 15(1)):91-111.DOI: 10.1016/j.rser.2010.09.040.

[2] 戴軍,單忠德,王西峰,等. 潮流水輪機的研究進展[J]. 可再生能源, 2010, 28(4): 130-133. DOI: 10.3969/j.issn.1671-5292.2010.04.031.

DAI Jun, SHAN Zhongde, WANG Xifeng, et al. Current research progress of water turbine[J]. Renewable Energy, 2010, 28(4): 130-133. DOI: 10.3969/j.issn.1671-5292.2010.04.031.

[3] LI Ye, CALISAL S M. Modeling of twin-turbinesystems with vertical axis tidal current turbines: Part I-Power output [J].Ocean Engineering, 2011, 38(4): 550-558. DOI: 10.1016/j.oceaneng.2010.11.025.

[4] 馬勇，張亮，馬良，等. 豎軸水輪機式潮流能發電裝置開發現狀與發展趨勢[J]. 科技導報, 2012, 30(12): 71-75. DOI: 10.3981/j.issn.1000-7857.2012.12.011.

MA Yong, ZHANG Liang, MA Liang，et al. Developing status and development trend of vertical axis turbinetype tidal current energy power generation device[J]. Science & Technology Review, 2012, 30(12): 71-75. DOI: 10.3981/j.issn.1000-7857.2012.12.011.

[5] 李志川.垂直軸潮流能水輪機水動力特性[D].哈爾濱：哈爾濱工程大學，2011 .

LI Zhichuan. Numerical simulation and experimental study on hydrodynamic characteristic of vertical axis tidal turbine[D].Harbin: Harbin Engineering University, 2011.

[6] JING Fengmei, XIAO Gang, MEHMOOD N, et al. Optimal selection of floating platform for tidal current power station[J]. Journal of Applied Science, Engineering and Technology, 2013 6(6): 1116-1121.

[7] YEUNG R W. Added mass and damping of a vertical cylinder in finite-depth waters[J]. Applied Ocean Research, 1981, 3(3):119-133. DOI: 10.1016/0141-1187(81)90101-2.

[8] LOPES D B S, SARMENTO A J N A, et al. Hydrodynamic coefficients of a submerged pulsating sphere in finite depth[J]. Ocean Engineering, 2002, 29(11):1391-1398. DOI: 10.1016/S0029-8018(01)00081-6.

[9] KRENK S. Time-domain analysis of frequency dependent inertial wave forces on cylinders[J]. Computers and Structures， 2013, 126: 184-192. DOI:10.1016/j.compstruc.2012.09.004.

[10]LI Yong, LIN Mian. Hydrodynamic coefficients induced by waves and currents for submerged circular cylinder[J]. Procedia Engineering, 2010, 4:253-261. DOI: 10.1016/j.proeng.2010.08.029.

[11]HU Peixin, WU G X, MA Q W, et al. Numerical simulation of nonlinear wave radiation by a moving vertical cylinder[J]. Ocean Engineering, 2002, 29(14):1733-1750. DOI: 10.1016/S0029-8018(02)00002-1.

[12]PAVON C L, IGLESIAS A S. Hydrodynamic coefficients and pressure loads on heave plates for semi-submersible floating offshore wind turbines: A comparative analysis using large scale models[J]. Renewable Energy, 2015, 81(7):864-881.

[13]GALLOWAY P W, MYERS L E, BAHAJ A S, Studies of a scale tidal turbine in close proximity to waves[C]//Proceedings of the 3rd International Conference and Exhibition on Ocean Energy. Bilbao：Deusto University, 2010:76-80.

[14]LUZNIK L, FLACK K A, LUST E E, et al. The effect of surface waves on the performance characteristics of a model tidal turbine [J]. Renewable Energy, 2013, 58:108-114. DOI: 10.1016/j.renene.2013.02.022.

[15]LUST E E, LUZNIK L, FLACK K A, et al. The influence of surface gravity waves on marine current turbine performance[J]. International Journal of Marine Energy, 2013,3-4: 27-40. DOI:10.1016/j.ijome.2013.11.003.

[16]陳良波， 鄭亞青．基于最小二乘法的曲線擬合研究[J]．無 錫 職 業 技 術 學 院 學 報，2012，11(5)：52-55. DOI: 10.3969/j.issn.1671-7880.2012.05.017.

CHEN Liangbo, ZHEN Yaqing. Study on curve fitting based on least square method [J]. Journal of Wuxi Institute of Technology, 2012, 11(5):52-55. DOI: 10.3969/j.issn.1671-7880.2012.05.017.

[17]HWANG I S, LEE Y H, KIM S J. Optimization of cycloidal water turbine and the performance improvement by individual blade control[J]. Applied Energy, 2009, 86(9):1532-1540. DOI: 10.1016/j.apenergy.2008.11.009.

Theeffectofpitchingmotiononthehydrodynamicperformanceofverticalaxisturbineunderdifferentspeedratios

WANG Kai, SUN Ke, ZHANG Liang

(Deepwater Engineering Research Center, Harbin Engineering University, Harbin 150001, China)

Floating vertical axis tidal current turbine(VATT) will occur pitching motion response in waves. To study the effect of pitching motion, a complex model of VATT moving in the waves is simplified to an impeller moving in the uniform current and superposed with harmonic motions, and the hydrodynamic performance of VATT is studied based on CFD viscous theory and ANSYS-CFX software, as well as the moving mesh and the sliding mesh. The CFX software is used to simulate the pitching motion under different speed ratio and rotating impeller is forced to pitch. The thrust coefficient and lateral force coefficient time history curves are also analyzed under different speed ratio by the method of least squares. The results show that, compared with turbine only rotating in uniform stream, the turbine under pitching motions has a little higher value in turbine’s energy utilization. The instantaneous fluctuation amplitude of the thrust and lateral force under pitching motion are obviously higher than that of turbine under uniform stream, which is bad for the structural strength and fatigue effect of turbine in waves. The damping force is the main ingredient to turbine under pitching motion and the effect of added mass force is small.

vertical axis turbine; pitching; damping coefficient; added mass coefficients; hydrodynamic performance; least squares

10.11918/j.issn.0367-6234.201604107

TK730，O352

A

0367-6234(2017)10-0145-08

2016-04-21

國家自然科學基金(11572094)；黑龍江省自然科學基金(E2016021)；上海交通大學海洋工程國家重點實驗室開放課題(1606)

王 凱(1989—) 男，博士研究生；

張 亮(1959—) 男，教授，博士生導師

孫 科，sunke@hrbeu.edu.cn

(編輯張 紅)