隱身反設計下飛翼布局氣動與隱身綜合設計

張 樂，周 洲，許曉平

(1.中國工程物理研究院 總體工程研究所，四川 綿陽621900；2. 西北工業大學 航空學院，西安710072)

隱身反設計下飛翼布局氣動與隱身綜合設計

張 樂1，周 洲2，許曉平2

(1.中國工程物理研究院 總體工程研究所，四川 綿陽621900；2. 西北工業大學 航空學院，西安710072)

為同時獲得良好的氣動和隱身性能，基于雙發動機布局下飛翼無人機大鼓包式機身，采用隱身反設計思路，開展了飛翼布局氣動與隱身綜合設計與分析研究，提出了一種減小翼型前緣半徑的機身前緣類“鷹嘴”形飛翼布局優化構型.分別采用CFD(計算流體力學)方法對M6機翼進行氣動數值模擬方法驗證，以及基于FEKO軟件中MLFMM(多層快速多極子方法)和PO(物理光學法)對圓柱體和某飛翼布局縮比模型進行隱身數值計算方法驗證，并利用該方法獲得了飛翼布局無人機氣動與隱身綜合特性.結果表明：建立的氣動與隱身數值模擬方法計算結果與實驗吻合較好，數值計算方法是可靠的；基于隱身反設計思路構建的機身前緣類“鷹嘴”形飛翼布局設計不僅縱向氣動特性略微提升，且前向(-25°～25°)隱身性能明顯提高，充分表明了隱身反設計思路的有效性；前緣類“鷹嘴”形設計主要影響機身表面壓力分布，并有助于提升升阻特性；前緣類“鷹嘴”形設計比傳統鈍形前緣設計在不同頻率和不同滾轉角下隱身特性均有所提高.

隱身反設計；飛翼布局；類“鷹嘴”形；氣動；隱身

飛翼布局具有高隱身性能與高氣動效率，且能夠提高突防能力并獲取空中優勢，因而受到人們越來越多的關注[1]，如美國正在研制的X-45[2]、X-47[3]等.為了具備更強的任務能力，飛翼布局常采用大展弦比的方式，如RQ180、RQ170等，這對飛翼布局的設計也提出了更大的挑戰.

截至目前，國內外對于飛翼布局開展了大量研究[4].在氣動設計方面，Hyoungjin等[5]對一體化翼身融合布局(BWB)進行了詳細的氣動特性分析；Mialon等[6]、甘文彪等[7]和Liebeck[8]分別針對飛翼構型進行了氣動設計及優化研究；鮑君波等[9]進行了飛翼布局氣動方案優選和試驗驗證.對于隱身特性方面，齊紅德等[10]開展了飛翼布局隱身特性數值模擬研究；張彬乾等[11]進行了飛翼布局隱身翼型優化設計.而對于氣動與隱身綜合研究方面，何開鋒等[12]開展了基于流體力學和電磁學方程數值求解的飛翼式飛機氣動隱身一體化設計研究；Lee等[13]采用并行遺傳算法對飛翼無人機開展了氣動隱身一體化設計；張德虎等[14]基于雙層代理模型開展了飛翼布局氣動隱身綜合設計；孫奕捷等[15]、Leifsson等[16]則分別結合飛翼布局飛機進行了氣動、隱身、控制等多學科優化設計研究.

上述列舉以及其他未列舉的與飛翼布局相關的研究工作均為飛翼布局無人機的氣動和隱身綜合設計提供了參考和借鑒，但其主要側重于小展弦比飛翼布局設計，或單發動機布局下飛翼布局設計研究，而基于大展弦比雙發飛翼布局，且在滿足無人機內部特殊裝載約束條件下(通常采用大鼓包式機身)進行氣動和隱身綜合設計研究的較少.本文正是基于此，并結合隱身反設計的思路開展氣動和隱身綜合設計研究與分析.

1 隱身反設計思路下飛翼布局優化構型設計

為了便于清晰地表述飛翼無人機各段翼面組成，如圖1所示定義了翼面上各段部件名稱.

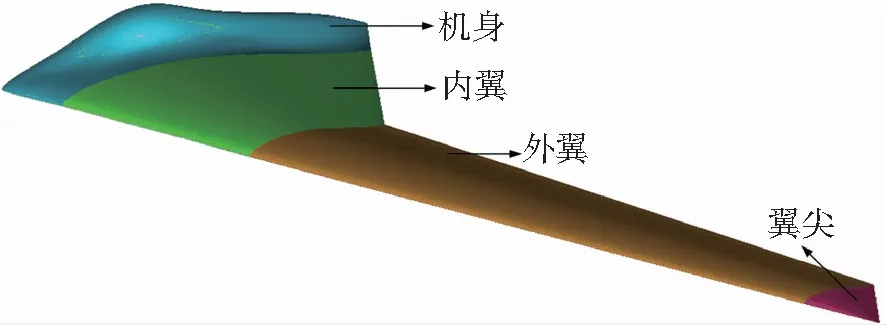
圖1 飛翼布局無人機翼面各部件定義

飛翼無人機一般翼身融合度較高，但在滿足任務載荷及內部特殊裝載(如衛通、合成孔徑雷達)等需求時，且考慮隱身需要，發動機完全深埋于機體內部，在對稱面上截面厚度較大，而內翼截面厚度相對較小，導致機身翼面會形成大鼓包.對翼型前緣設計而言，傳統設計思路一般是前緣半徑較大，這樣有助于緩和前緣流動加速情況，逆壓梯度相對更小，從而使得較大迎角范圍下流動仍是附著的，失速迎角也會增大.綜合上述兩點，可以開展大展弦比飛翼布局初始構型設計(如圖2所示).由圖2可看出，初始構型機身前緣曲率較大(前緣呈鈍形)，由對稱截面向內翼截面曲面過渡時曲率變化較大，機身前緣在前向會產生較強的鏡面反射，不利于前向隱身，且無人機最主要升力面為外翼和內翼，在保證高升、阻比特性及滿足特殊裝載約束下，為了進一步縮減前向雷達散射截面(radar cross section，RCS)，可僅針對無人機大鼓包機身開展優化修形設計.

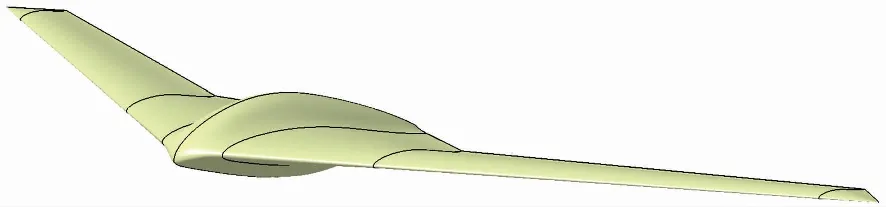
圖2 飛翼布局初始構型

反設計思路已經非常成熟地應用于飛機氣動設計中，在飛翼布局初始構型的基礎上，考慮其大鼓包機身會極大降低無人機前向角域RCS，為提升其隱身性能，提出一種基于隱身反設計思路的大展弦比飛翼布局設計.隱身反設計準則是在保持飛翼布局高升阻比前提下，僅對大鼓包機身開展合理的優化修形設計(主要基于鈍形前緣)，從而改變翼面上電磁散射分布，將機身鈍前緣強鏡面反射削減為尖頂散射、邊緣繞射等弱散射.本文隱身反設計詳細思路為：首先，分別開展飛翼無人機初始構型的氣動和隱身特性分析；從中提取無人機翼面上強電磁散射源分布；然后，在滿足內部特殊裝載布置約束下，基于獲取的強電磁散射區域，重點針對對稱截面、內翼與機身交接截面進行優化修形設計；最終，在滿足無人機內部裝載約束后，對無人機機身翼面進行一定的曲率控制(為避免形成強鏡面反射，曲率盡量保持更平緩的過渡).

基于以上隱身反設計思路，提出了一種減小翼型前緣半徑的類“鷹嘴”形前緣設計，建立了飛翼布局優化構型，如圖3所示.這種尖前緣設計可以有助于減小無人機前向和側向RCS，尤其可能會顯著提升前向隱身性能.另外，這種前緣設計可能會產生抬頭力矩，從而有助于無人機的自配平.但同時，翼型前緣半徑的減小，可能會導致氣動性能在低速大迎角狀態下下降較快，不過在高速下影響可能相對較小，因此，這種前緣設計主要在機身應用.

圖3 飛翼布局優化構型

飛翼無人機優化構型與初始構型在機身對稱截面、內翼與機身交接面處對比如圖4所示，圖4中Fw-opt為飛翼布局優化構型，Fw-initial為飛翼布局初始構型.對比可知，飛翼無人機優化構型與初始構型截面弦長不變，隱身反設計思路下將機身前緣由鈍形設計為類“鷹嘴”形，前緣曲率半徑顯著減小，這是本文優化修行設計最重要的部分；另外，在滿足機身內部裝載約束前提下，優化構型機身對稱截面處最大厚度略微下降，且其截面后段厚度略微縮小.考慮到采用減小翼型前緣半徑設計時，無人機前緣更易形成流動分離，在低速大迎角狀態下氣動性能可能會有一定程度惡化，因此，從機身對稱截面向內翼過渡時，需要對機身展向截面前緣進行適當的修形.優化修形設計時，為了抑制一定的前緣流動分離，并保證在過渡段(由機身對稱截面至內翼與機身交接面)前緣曲率平緩過渡，本文在內翼與機身交接截面采用下表面尖前緣和上表面鈍形前緣的組合修形設計.

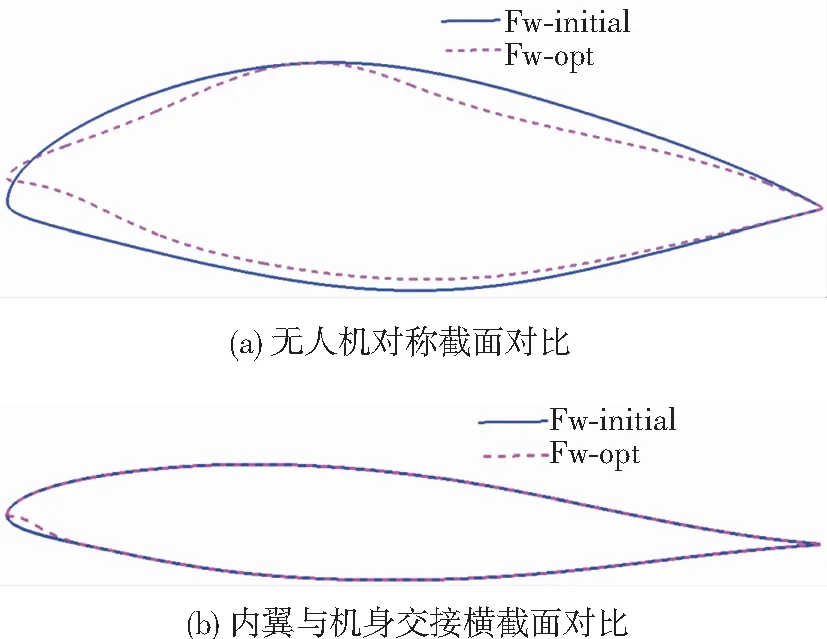
圖4 飛翼無人機初始構型與優化構型兩個典型截面對比

Fig.4 Typical section comparison between initial and optimization model of flying wing UAV

2 氣動與隱身計算方法及驗證

2.1 氣動計算方法及驗證

針對大展弦比飛翼布局氣動數值模擬，計算采用三維雷諾平均可壓縮N-S(Navier-Stokes)方程，使用有限體積法對控制方程進行離散，其中無黏對流通量采用Roe格式，黏性通量采用二階中心差分，湍流模型為k-ωSST.選用ONERA M6機翼繞流場進行氣動數值計算方法可靠性驗證，參考已有的實驗數據[17]，考慮到飛翼無人機在飛行狀態右邊界(如Ma=0.75或Ma=0.70)或大迎角狀態下可能會產生較強激波，因而選擇相近的亞音速狀態進行計算：迎角α=3.06°，馬赫數Ma=0.839 5，雷諾數Re=1.172×107.參考實驗數據的Ma和Re略高于飛翼布局無人機，但著重關注氣動計算方法對于激波強度和位置的捕捉能力.計算采用網格結點為289×65×49的C-H型結構網格，考慮到黏性計算的需要，需保證近物面Y+=1，其中遠場邊界大小分別為展長和弦長20倍，計算網格如圖5所示，在機翼前緣、后和附面層上計算網格都進行了加密處理.

M6機翼氣動數值計算結果與實驗結果表面壓力分布對比如圖6所示.對比可知，數值計算在4種典型截面上流動特性與實驗結果比較吻合，各截面處激波強度與位置捕捉均較好.整體而言，選取的數值計算方法能夠較準確捕捉流場特點，該計算時可靠有效的.

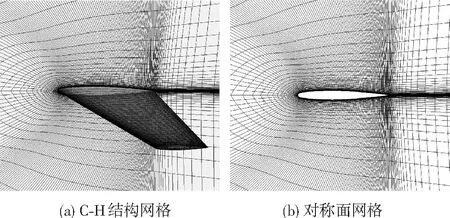
圖5 ONERA M6機翼計算網格

對于本文飛翼無人機，氣動計算方法與M6機翼計算相同，其中網格剖分仍保證近物面Y+≈1，飛行高度20 km，飛行Ma=0.6，壓力遠場邊界湍流強度為0.2%，湍流黏性比為2，邊界條件還包括對稱面和固壁等.

2.2 隱身計算方法及驗證

大展弦比飛翼布局在不同頻段下呈現的電尺寸特性是不同的，本文主要選取L、S、C波段下的典型頻率1、3、6 GHz進行隱身計算.國內外對于各種電尺寸目標隱身計算方法主要分為低頻積分和高頻近似兩類.其中低頻算法適用于任何激勵下的任意幾何形狀，考慮了各子散射體之間強電磁互耦，能夠精確求解任意復雜目標的電磁散射問題，但受計算資源和效率限制，僅適用于電小或電中尺寸計算，而高頻近似方法則忽略子散射體之間的電磁互耦，計算精度稍差，適用于高頻下計算.本文將采用成熟的商業軟件FEKO，并選取MLFMM(多層快速多極子，低頻算法)和PO(物理光學發，高頻算法)進行計算.為了驗證所采用隱身算法的有效性，分別選取圓柱體和某飛翼布局縮比模型進行對比驗證，計算坐標系與文獻[18]相同.

2.2.1 圓柱體隱身計算方法驗證

驗證計算選取經典圓柱體金屬模型[19]，其長度為711 mm，直徑為140 mm，計算頻率為5.4 GHz，計算角度θ=0°，φ=0°～180°(其中θ為水平面入射角度，φ為俯仰方向入射角度(計算角度坐標系參考文獻[18]所示))，計算采用垂直極化方式，網格量約768 86.圖7、8給出了圓柱體計算結果與實驗結果對比，由圖可知，MLFMM和PO算法計算RCS與實驗結果吻合較好.另外，MLFMM算法較PO算法在各個入射角度上計算的RCS變化趨勢更吻合，其中PO算法計算所得RCS變化曲線較MLFMM方法“零深點”(波谷點)明顯更多，這主要因為PO算法會忽略邊緣繞射、尖頂散射等而僅僅計算表面的鏡面反射，從而導致在局部入射角域RCS會明顯偏小.

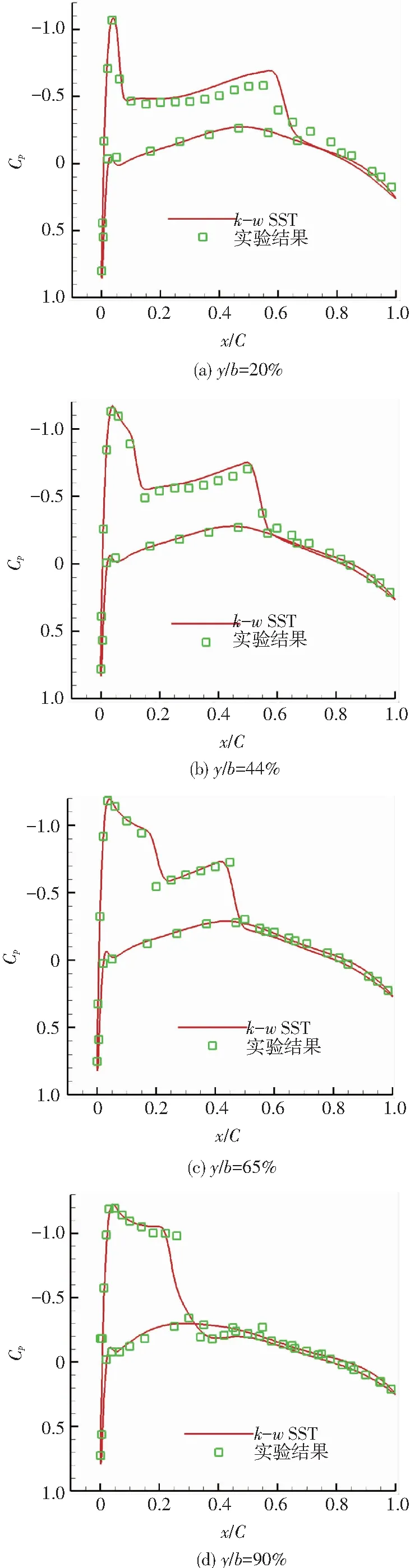
圖6 M6機翼數值計算壓力分布與實驗結果對比

Fig.6 Pressure distribution comparison between computational and experimental result of M6 wing

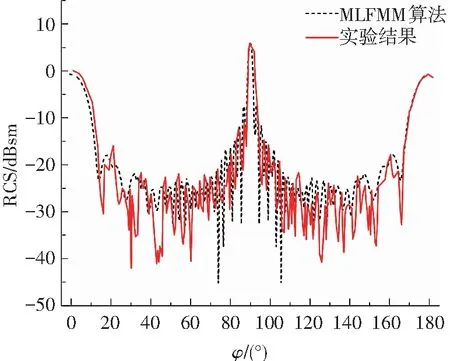
圖7 圓柱體模型實驗與MLFMM算法計算結果對比

Fig.7 Comparison between experimental and computational result with MLFMM of cylinder model

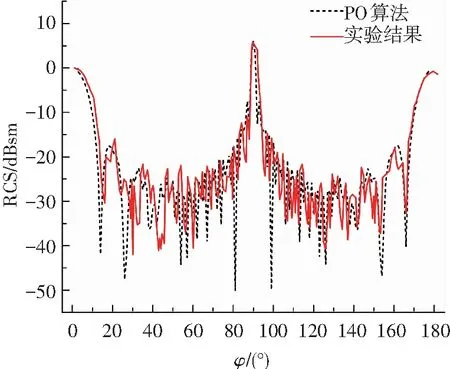
圖8 圓柱體模型實驗與PO算法計算結果對比

Fig.8 Comparison between experimental and computational result with PO of cylinder model

2.2.2 某飛翼布局縮比模型隱身試驗驗證

為了驗證所采用隱身算法對于大展弦比飛翼布局無人機電磁散射特性計算的可靠性，選取某縮比飛翼模型(與本文飛翼布局初始構型接近)進行測試與計算對比.表1所示為飛翼布局縮比模型實驗與仿真計算RCS均值對比(垂直極化).

表1某飛翼布局無人機實驗與仿真計算RCS均值對比

Tab.1 Mean value of RCS between experimental and computational result of flying wing UAV

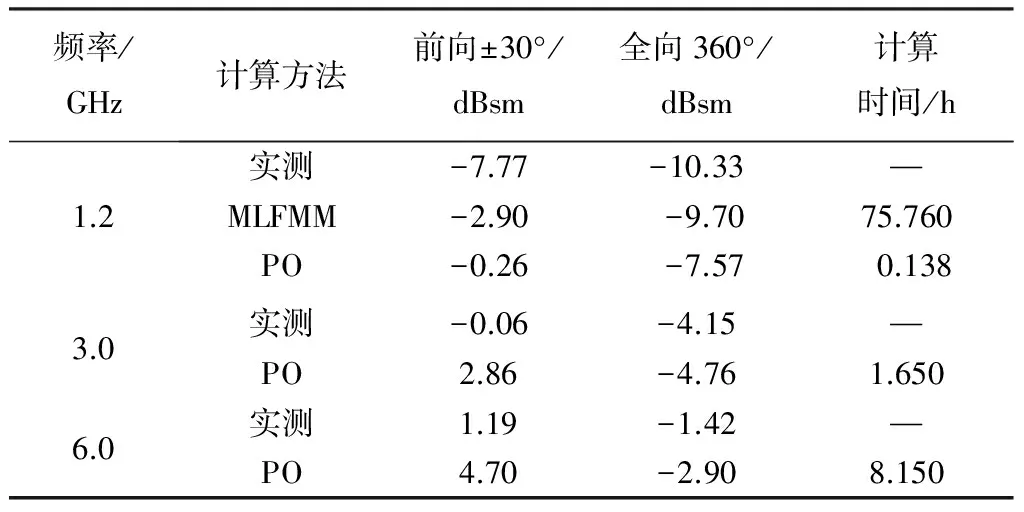
頻率/GHz計算方法前向±30°/dBsm全向360°/dBsm計算時間/h1．2實測-7．77-10．33—MLFMM-2．90-9．7075．760PO-0．26-7．570．1383．0實測-0．06-4．15—PO2．86-4．761．6506．0實測1．19-1．42—PO4．70-2．908．150

由表1可知，在頻率1.2 GHz下，與實驗結果相比，MLFMM算法計算結果比PO算法吻合更好，計算精度也更高，但整體上兩種算法RCS值差距不大.尤其隨著頻率增加，MLFMM算法需要的計算內存劇增且計算時間增長較快，在散射目標電尺寸進一步增加時，PO能夠滿足一定計算要求，可選擇PO算法進行計算.由表1還可知，整體上看，在頻率3.0、6.0 GHz下，采用PO算法計算的RCS均值與實驗結果還是吻合較好的，能夠反映出RCS變化的整體趨勢.

對于本文飛翼無人機，隱身計算采用水平極化方式，并采用單站RCS計算，且兩種算法都采用三角形面元網格，網格尺寸按照λ/6(λ為入射電磁波波長)劃分.

3 結果與分析

3.1 機身前緣類“鷹嘴”形和鈍形設計氣動性能分析

3.1.1 宏觀氣動性能結果對比

飛翼布局優化構型和初始構型的縱向基本氣動特性對比如圖9所示，由圖9可知，在迎角-2°～6°內，兩種構型升力系數和俯仰力矩系數(力矩參考點為(6 m,0,0))變化為線性的，迎角進一步增大后立即轉為非線性；而且還可以看到，在線性段，初始構型的升力系數略高于優化構型，但相應的阻力系數也有所增加，最終表現為優化構型升、阻比略大于初始構型，升、阻特性是變好的，從而也可以反映出隱身反設計思路下的飛翼布局優化構型設計達到了預期的目標.

3.1.2 表面壓力分布分析

為了更加詳細地分析表面壓力變化，選取圖10所示3個典型截面位置壓力系數進行對比.

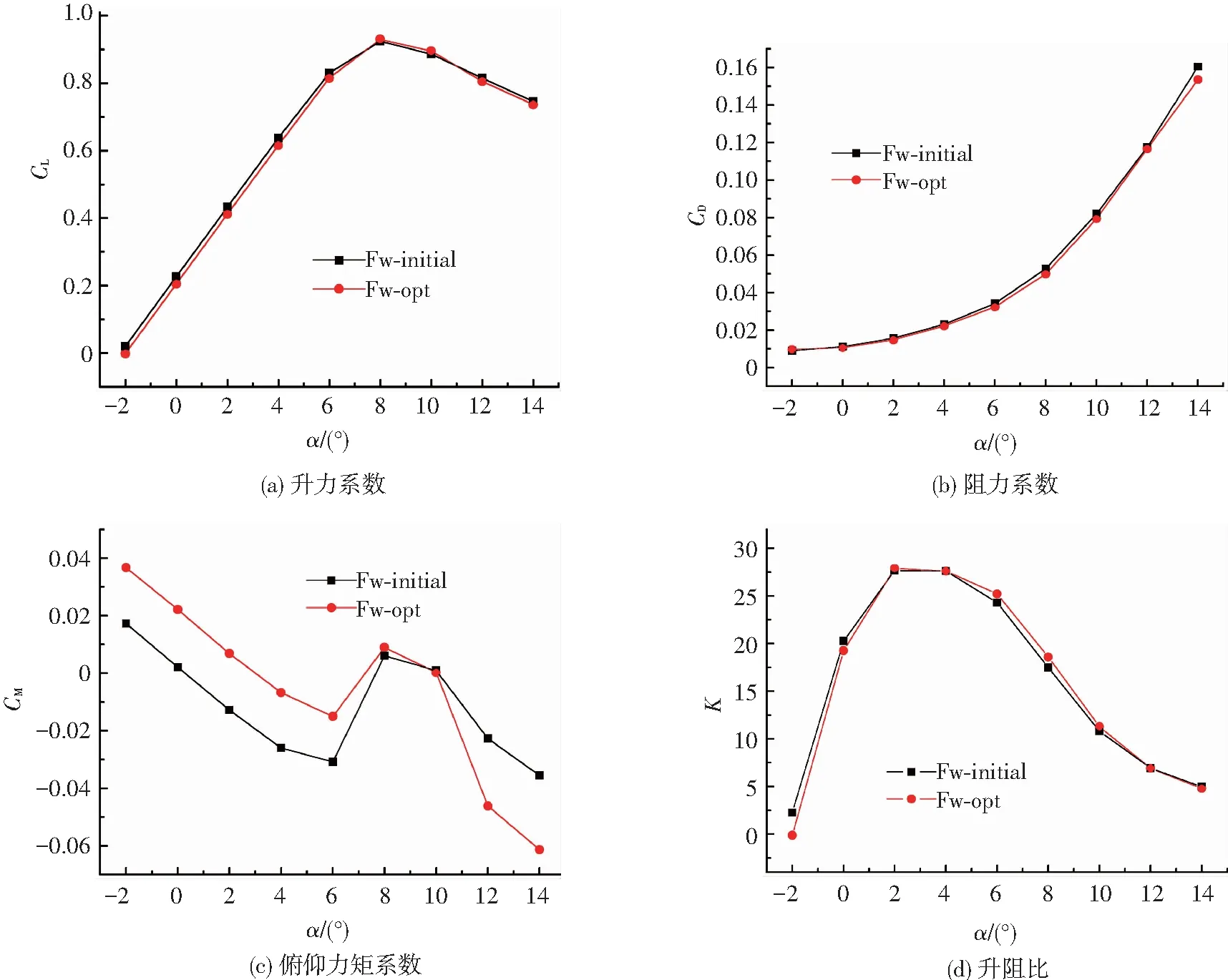
圖9 飛翼布局優化構型與初始構型縱向基本特性對比

圖10飛翼布局3個典型截面位置示意(未完全顯示外翼和翼尖)

Fig.10 Three typical spanwise locations of flying wing UAV

飛翼布局兩種構型在3個典型截面上壓力分布(迎角2°時)對比如圖11所示.對比圖11(a)、(b)可知，優化構型在機身上兩個截面壓力變化較明顯，也進一步可以看出飛翼布局機身曲面曲率變化較劇烈.由對稱面壓力分布對比可知，初始構型從前緣到弦向5%之間會形成負升力，這主要是因為其在對稱截面位置前緣是稍微向下傾斜的，導致形成的駐點在對稱截面的上翼段；而優化構型經過了優化修形設計后在對稱截面的前段升力會有所增加.另外，飛翼布局優化構型在對稱截面和展向5%截面上弦向中間位置附近后段下翼面壓力明顯小于上翼面，反映出了典型的反彎翼型翼面壓力分布特征.優化構型在截面后段會形成負升力，升力有所下降，不過會產生一定的抬頭力矩，有助于飛翼布局進行自配平.

由圖11(c)可知，在展向截面18%位置上，兩種構型上翼面表面壓力分布基本完全相同，而下翼面只在從前緣點到弦向15%處有所差異，這主要是因為兩種構型內翼上只在內翼與機身交接截面有所略微不同(參考如圖4(b)所示外形對比)，而內翼與外翼交界面和整個外翼段是不變的，所以導致了內翼段的表面壓力幾乎是不變的；另外，由圖11還可知，內翼段截面設計時仍保持了反彎翼型表面壓力分布的特點，在弦向80%位置附近上、下翼面壓力是反向的.

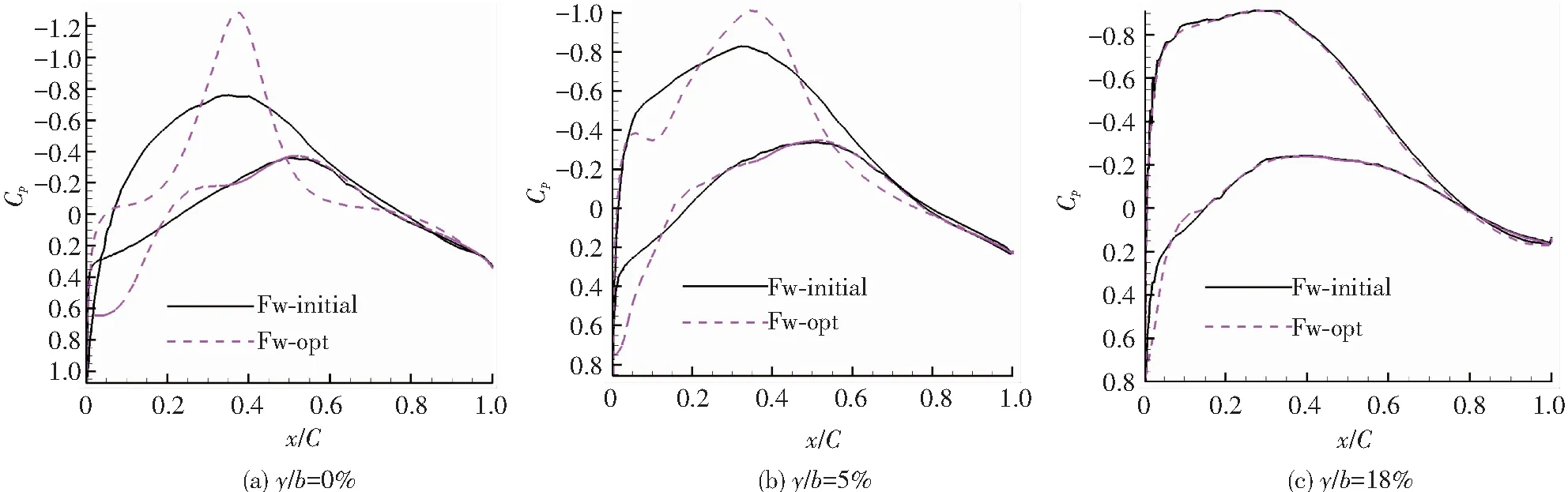
圖11 迎角2°下3個典型截面壓力分布對比

3.1.3 極限流線分析

飛翼布局無人機優化構型和初始構型上翼面在3個典型迎角下的極限流線分布如圖12所示，旨在詳細分析飛翼布局翼面上流動發展情況.

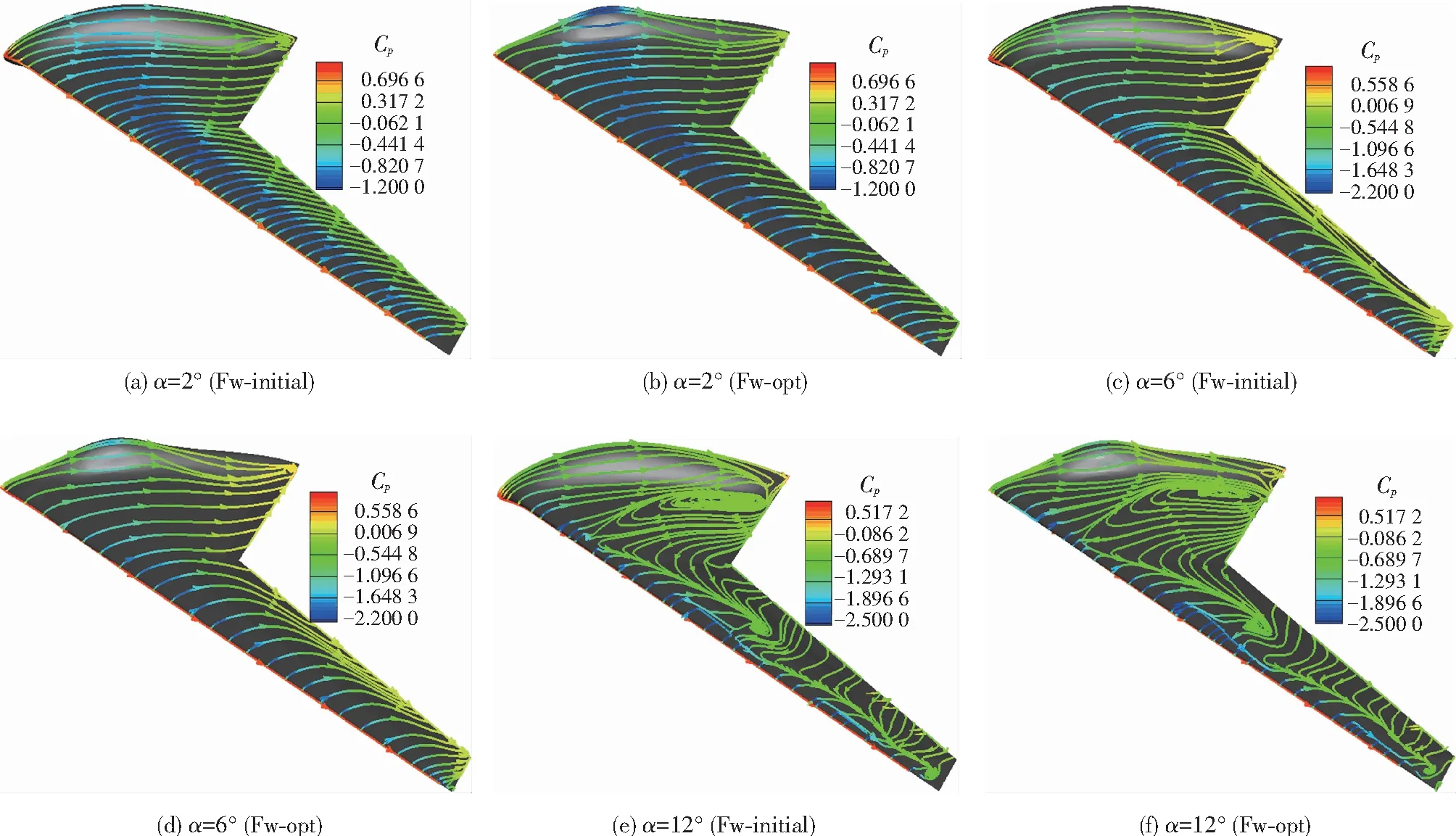
圖12 3個典型迎角下兩種構型翼面極限流線對比

分析圖12(a)、(b)可知，在巡航迎角2°下，飛翼布局兩種構型沿順流方向均基本表現為附著流動，僅僅在機身上極限流線具有一定的偏折，這是因為機身上大鼓包的存在導致其對來流形成一定的阻滯作用；由圖12還可知，兩種構型在機身上翼面后緣位置附近發生了一定的流動分離，而優化構型流動分離區域更小，其主要是由于后緣表面壓力分布造成的，機身大鼓包后段形成的流向壓力梯度與機身后掠產生的展向壓力梯度相互作用，從而導致了流動分離現象發生在機身后緣壓力恢復區.

分析圖12(c)、(d)可知，迎角6°下兩種構型內翼和外翼后緣分別形成了沿展向反方向(從翼尖到機身對稱面)和展向方向的流動.分析圖12(c)可知，初始構型在后掠翼展向壓力梯度的驅使下，且沿流動方向邊界層能量慢慢有所損失，進而使得外翼段后緣翼根位置具有一定的展向流動，但是其流線只是略微有所彎曲.另外，初始構型在外翼段后緣附近已經形成了明顯的流動分離，且產生了較清晰的分離線，不過優化構型在外翼后緣處流動分離線顯然是靠后的；由此還可看到，翼尖和外翼翼根上仍表現為沿來流方向的附著流動，這是由于受到翼尖渦影響，附近流體之間的摻混會進一步加強，翼尖位置的主流能量也會得到增強，因而克服逆壓梯度的能力自然也會提升，最終表現在翼尖流動有所改善.

分析圖12(e)、(f)可知，兩種構型翼面上分離線隨著迎角增大逐漸向前緣方向以及外翼翼根方向移動，當迎角達到12°時，外翼翼面上呈現兩條非常明顯的分離線，且其靠近翼梢位置的分離線明顯更接近前緣位置，另外，靠近外翼翼根的分離線在外翼中段產生小漩渦，而翼尖段呈現了典型的分離螺旋點；同樣地，內翼段受到外翼翼根分離區的影響，展向逆壓梯度會進一步增大，最終表現在內翼后段產生具有明顯的分離旋渦并翼面上具有大面積倒流現象，除了機身，無人機其余翼面流場結構均相當復雜.整體而言，在大迎角12°狀態下，飛翼布局兩種構型流場特性類似，不過優化構型在外翼翼面上兩條分離線比初始構型更加靠后，縱向氣動特性更好.

3.2 機身前緣類“鷹嘴”形和鈍形設計隱身性能對比

3.2.1 不同頻率下隱身特性對比

3個典型頻率下飛翼布局優化構型和初始構型RCS對比如圖13～15所示.綜合圖13～15可知，在前向角域0°～25°內(橢圓圈內所示)，優化構型RCS較初始構型明顯減小，充分體現了隱身反設計思路是有效的.

首先，可以發現，飛翼布局兩種構型在不同頻率下隨著電磁波入射角度變化時整體RCS值變化規律基本保持一致，全向360°角域內均具有6個峰值點，也即在0°～180°角域內有3個強散射點(垂直前緣方向、垂直內翼后緣方向、垂直外翼后緣方向).但是，其雖然形成了3個較強散射峰值點，但飛翼無人機整個翼面上呈現的強散射方向一般都在較集中的方位角上，強散射角域基本都是非常狹窄的，也就導致了在波峰之間的雷達回波信號其實是非常弱的，敵方雷達難以接受到連續的信號，最終也就降低了飛翼無人機被探測到的概率.

其次，當雷達頻率增加時，由于前緣強鏡面反射的高頻效應作用(頻率增大，鏡面反射強度隨之增強)，垂直飛翼無人機前緣后掠角方向RCS峰值慢慢增大.顯然，由圖還可呈現出飛翼布局無人機一定的RCS頻率特性變化，隨著頻率增加，RCS振蕩特性有所緩解；以前向角域0°～30°RCS變化為例，飛機RCS頻率變化特性可從不同頻率下RCS特性展現，其主要原因是當飛翼布局局部尺寸與雷達波長數量級相當，散射目標就在“諧振區”內，隨著頻率增大，雷達波長逐漸減小，并逐漸遠遠小于散射目標幾何尺寸，然后散射體就會處于“光學區”.

圖13 頻率1 GHz下飛翼布局初始構型與優化構型RCS對比

Fig.13 RCS comparison between initial and optimization model of flying wing UAV at the frequency of 1 GHz

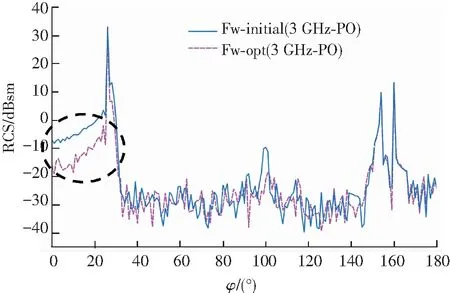
圖14 頻率3 GHz下飛翼布局初始構型與優化構型RCS對比

Fig.14 RCS comparison between initial and optimization model of flying wing UAV at the frequency of 3 GHz

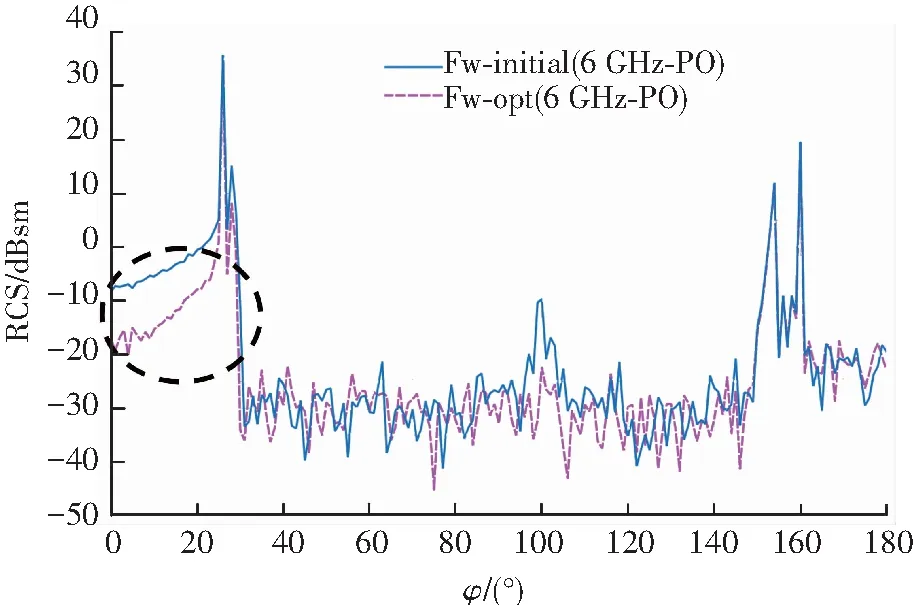
圖15 頻率6 GHz下飛翼布局初始構型與優化構型RCS對比

Fig.15 RCS comparison between initial and optimization model of flying wing UAV at the frequency of 6 GHz

然后，分析同一飛翼布局，以優化構型舉例，其在同一雷達波入射角下不同頻率時RCS變化規律是不一致的，如1 GHz頻率下，入射角58°附近會產生局部小波峰，而在3、6 GHz頻率下，在入射角度100°附近才產生小波峰，這是因為入射角58°時電磁散射相干疊加主要由機身前部和機遇前緣形成，而入射角100°時，無人機還具有機身后緣和機翼后緣電磁散射共同疊加，電磁散射也更加復雜，各個局部子散射體在不同角域下的相干散射疊加隨著頻率變化隱身特性漸漸表現出差異性.

整體上看，建立在隱身反設計思路上設計的優化構型前向RCS(主要為0°～25°)比初始構型明顯縮減，不過在其他角域上互有增減，但是RCS變化幅度都非常小，飛翼布局優化構型隱身特性明顯更優異.

3.2.2 表面電流分析

飛翼布局優化構型和初始構型在頻率1 GHz下局部表面電流對比(電磁波從正前向入射)如圖16所示，通過電流分布可分析翼面上各散射區域的分布.

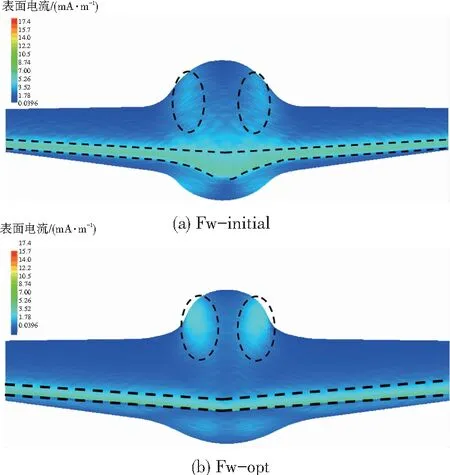
圖16 正前向(φ=0°)入射時飛翼布局兩種構型表面電流對比

Fig.16 Surface current comparison between initial and optimization model of flying wing UAV at thefront

由圖16可知，初始構型表面強電流集中在無人機前緣區域、機頭區域、內翼與機身交接面向鼓包最大厚度過渡區域(圖16(a)虛線所示)，而優化構型則主要集中在飛機前緣區域和機身兩側大鼓包區域(圖16(b)虛線所示)，整個無人機強電磁散射區域也主要分布在這些方向.通過分析兩種構型主要散射源分布區域可知，初始構型在整個鈍形前緣區域表面曲率變化劇烈，會形成很強的鏡面反射，不過優化構型在機身前緣設計為類“鷹嘴”形，表面曲率明顯減小，導致表面電流會主要匯聚于極窄的尖前緣表面，但是同樣地，優化構型機身大鼓包向內翼過渡時曲率下降較大，仍然會形成較強反射.整體而言，初始構型翼面上強表面電流區和電流強度都是顯著大于優化構型的，這與優化構型在前向RCS縮減是相互對應的(參考表面壓力分布分析).

為了定量分析飛翼布局在不同頻率和不同角域內隱身性能，表2給出了優化構型和初始構型在水平極化方式下RCS均值對比(前向±20°代表前向-20°～20°角域).由表2可知，優化構型在3個不同角域范圍RCS均值與RCS峰值基本上都小于初始構型，其中前向±20°RCS均值下降幅度最明顯，這也從定量上進一步反映出隱身反設計思路是有效的.

由表2還可知，對比不同頻率下RCS峰值，兩種構型峰值都較高(>29 dBsm)，這是由于本文飛翼無人機采用大展弦比布局，且前緣呈現單個長條形(僅有一個后掠角)，也就導致了前緣方向會累積相當強的雷達散射.再對比前向±20°和±30°角域RCS均值，優化構型在前向±20°角域隱身性能顯著優于初始構型，但在前向±30°角域隱身性能卻僅略微提升，這是由于垂直前緣(約26°)RCS峰值巨大，基于“湮沒”其余入射角下散射；另外，在3個頻率下優化構型在前向±20°RCS均值基本接近-10 dBsm，在表面使用純金屬前提下，本文大展弦比飛翼布局隱身性能是非常良好的.

表2水平極化下飛翼布局兩種構型RCS均值(不同角域內)

Tab.2 Mean value of RCS between experimental and computational result of flying wing UAV at different azimuth angles (HH)

頻率/GHz模型峰值/dBsm前向±20°/dBsm前向±30°/dBsm全向360°/dBsm1Fw?initial30．0-3．4315．328．29Fw?opt29．4-9．8014．627．743Fw?initial33．1-4．4218．3010．70Fw?opt32．0-13．0117．139．566Fw?initial35．8-4．3620．9513．41Fw?opt35．0-12．9720．1012．58

3.2.3 滾轉狀態下隱身特性對比

飛行器在執行復雜任務時，進入滾轉狀態有時難以避免，所以完全有必要開展飛翼無人機在不同滾轉狀態下隱身特性研究.選取飛翼布局右滾轉5°(順時針滾轉)，計算頻率3 GHz，選取雷達波入射角度為θ=-90°，φ=0°～360°(滾裝狀態下全機左右不對稱)，并采用水平極化方式.計算方法采用PO算法，網格劃分與前文相同，圖17給出了飛翼布局優化構型與初始構型在極坐標下RCS對比.

由圖17可知，飛翼布局優化構型在前向角域-30°～30°內RCS值明顯小于初始構型(虛線框標示)，但在其他角域內RCS僅略微互有增減，整體而言，優化構型仍保持良好的隱身特性.另外，飛翼布局初始構型在右滾轉5°下全機左側和右側入射角度下RCS峰值為22.1、24.0 dBsm，而優化構型則分別為22.0、21.9 dBsm，相比于不滾轉狀態(表面電流分析中)，兩種構型RCS峰值減小幅度達到約10 dBsm，這是因為滾轉狀態下飛機強鏡面反射會逐漸減弱引起的.由圖17還可知，對于同一飛翼無人機，滾轉狀態下無人機左右兩側入射方向的隱身性能也存在差異，甚至在局部入射角度上差距較大，如優化構型在入射角度約100°處RCS明顯大于約260°處RCS(無滾轉時應該相等)，這是因為滾轉狀態下機翼前緣、機身大鼓包等散射相干疊加不同造成的.

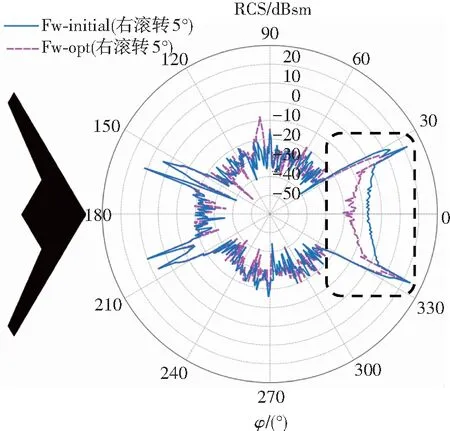
圖17 飛翼布局優化與初始構型右滾轉5°下RCS對比

Fig.17 RCS comparison between initial and optimization model of flying wing UAV at therolling angle of 5°

4 結 論

1)基于隱身反設計思路建立的機身前緣類“鷹嘴”形設計不僅氣動特性略微提升，且前向(尤其是前向±25°)隱身性能明顯提高，充分表明了隱身反設計思路的有效性.

2)機身前緣類“鷹嘴”形設計主要影響機身段表面壓力分布，并會在前緣前段形成抬頭力矩，有利于飛機的自配平.

3)機身前緣類“鷹嘴”形設計在不同頻率和各個角域內RCS均值較機身前緣鈍形設計均有所下降，尤其表現在前向±20°RCS均值明顯下降，這主要因為機體表面強電流區明顯縮減.

[1] AUSTIN R. Unmanned aircraft systems: UAVS design, development and deployment[M]. New York: John Wiley & Sons Inc., 2010:113-118. DOI: 10.1002/9780470664797.

[2] WISE K A，LAVRETSKY E. Robust and adaptive control of X-45A J-UCAS：A design trade study[C]//Proceedings of the 18th IFAC World Congress. Milano，Italy：IFAC Secretariat，2011：6555-6560. 10.3182/20110828-6-IT-1002.00716.

[3] 張航, 譚慧俊, 李湘萍. 類 X-47 狹縫式進氣道的流動特征與工作性能[J]. 航空學報，2009, 30(12): 2243- 2249.

ZHANG Hang，TAN Huijun，LI Xiangping. Flow structure and performance characteristics of X-47-like slot-shaped inlet [J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(12): 2243-2249.

[4] WOOD R M, BAUER S X S. Flying wings/flying fuselage, AIAA-2001-0311[R]. Reston: AIAA, 2001.

[5]HYOUNGJINK, LIOU M S. Flow Simulation of N2B Hybrid Wing Body Configuration,AIAA 2012-0838[R].[S.L.]:AIAA,2012.

[6] MIALON B, FOL T, BONNAUD C. Aerodynamic optimization of subsonic flying wing configurations, AIAA-2002-2931[R]. Reston: AIAA,2002.

[7]甘文彪, 周洲, 許曉平.基于準則的大展弦比飛翼氣動設計[J].北京航空航天大學學報, 2015, 41(9): 1608-1614. DOI:10.13700/j.bh.1001-5965.2014.0672.

GAN Wenbiao, ZHOU Zhou, XU Xiaoping. Aerodynamic design of high-aspect-ratio flying wing based on criteria[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(9): 1608-1614. DOI:10.13700/j.bh.1001-5965.2014.0672.

[8] LIEBECK R H. Design of the blended wing body subsonic transport[J]. Journal of Aircraft, 2004, 41(1):10-25.DOI: 10.2514/1.9084.

[9] 鮑君波, 王鋼林, 武哲.飛翼布局氣動方案優選和試驗驗證[J].北京航空航天大學學報, 2012, 38(2): 180-184.DOI:10.13700/j.bh.1001-5965.2012.02.021.

BAO Junbo, WANG Ganglin, WU Zhe. Optimization and experimental verification for aerodynamic scheme of flying-wing[J]． Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2) : 180-184. DOI:10.13700/j.bh. 1001-5965.2012.02.021.

[10]齊紅德, 岳奎志, 郁大照. 飛翼隱身特性數值模擬[J].海軍航空工程學院學報,2015, 30(3): 258-262. DOI:10.7682/j.issn. 1673-1522.2015.03.011.

QI Hongde, YUE Kuizhi, YU Dazhao. Numerical simulation of the flying wing stealth[J]. Journal of Naval Aeronautical and Astronautical University, 2015, 30(3): 258-262. DOI:10.7682/j.issn.1673-1522.2015.03.011.

[11]張彬乾, 羅烈, 陳真利，等.飛翼布局隱身翼型優化設計[J].航空學報, 2014, 35(4): 957-967. DOI:10.7527/s1000-6893.2013.0429.

ZHANG Binqian, LUO lie, CHEN Zhenli, et al. On stealth airfoil optimization design for flying wing configuration[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 957-967. DOI:10.7527/s1000-6893.2013.0429.

[12]何開鋒, 錢煒祺, 陳堅強，等. 基于流體力學和電磁學方程數值求解的飛行器氣動隱身一體化設計[J].空氣動力學學報, 2009, 27(2): 180-185. DOI: 10.3969/j.issn.0258-1825. 2009.02.007.

HE Kaifeng, QIAN Weiqi, CHEN Jianqiang, et al. Integrated aircraft design of aerodynamic and stealthy performance with numerically solving fluid dynamics and electro-magnetics equations[J]. Acta Aerodynamic Sinica, 2009, 27(2):180-185. DOI: 10.3969/j.issn.0258-1825.2009.02.007.

[13]LEE D S, GONZALE L F, SRINIVAS K, et al. Aerodynamic/RCS shape optimization of Unmanned Aerial Vehicles using Hierarchical Asynchronous Parallel Evolutionary Algorithms[C]//Proceedings of the 24th Applied Aerodynamics Conference. San Francisco: AIAA, 2006.

[14]張德虎,高正紅,李焦贊,等. 基于雙層代理模型的無人機氣動隱身綜合設計[J].空氣動力學學報,2013, 31(3):394-400.

ZHANG Dehu, GAO Zhenghong, LI Jiaozan, et al. Aerodynamic and stealth synthesis design optimization of UAV based on double-stage metamodel[J]. Acta Aerodynamic Sinica, 2013, 31(3):394-400.

[15]孫奕捷,申功璋. 飛翼布局飛機控制/氣動/隱身多學科優化設計[J],北京航空航天大學學報,2009,35 (11):1357-1360.

SUN Yijie, SHEN Gongzhang. Multidisciplinary optimization of control-aerodynamic-stealth for flying wing aircraft design [J]. Journal of Beijing University of Aeronautics and Astronautics, 2009,35 (11):1357-1360.

[16]LEIFSSONL, KO A, MASON W H, et al. Multidisciplinary design optimization of blended wing body transport aircraft with distributed propulsion[J]. Aerospace Science and Technology, 2013, 25(1):16-28. DOI: 10.1016/j.ast.2011. 12.004.

[17]SCHMITT V, CHARPIN F. Pressure Distributions on the ONERA-M6-Wing at Transonic Mach Numbers,AGARD-AR 138[R].[S.L.]:[S.n.],1979.

[18]張樂, 周洲, 許曉平,等. 飛翼無人機3種保形進氣口進氣道氣動與隱身綜合特性對比[J]. 航空動力學報, 2015, 30(7): 1651-1660. Doi:10.13224/j.cnki.jasp.2015.07.017.

ZHANG Le, ZHOU Zhou, XU Xiaoping, et al. Comparison on aerodynamic and stealthy performance of flying wing unmanned aerial vehicle with three conformal intake inlets[J]. Journal of Aerospace Power, 2015, 30(7): 1651-1660. DOI:10.13224/j.cnki.jasp.2015.07.017.

[19]阮穎錚. 雷達截面與隱身技術[M]. 北京: 國防工業出版社, 2000.

Integrateddesignonaerodynamicandstealthyofflyingwingunmannedaerialvehiclebasedonstealthyinversedesignmethod

ZHANG Le1, ZHOU Zhou2, XU Xiaoping2

(1.Institute of Systems Engineering, CAEP, Mianyang 621900, Sichuan, China；2.College of Aeronautics,Northwestern Polytechnical University, Xi’an 710072, China)

To obtain both good performance on both aerodynamic and stealthy, integrated design and analysis on aerodynamic and stealthy characteristics for flying wing unmanned aerial vehicle(UAV) is conducted based on stealthy inverse design method, focusing on the big bump in the fuselage of twin-engine layout flying wing UAV. Then a kind of fuselage with leading edge similar to eagle mouth is proposed, whose leading edge radius of airfoil is decreased. Using computational fluid dynamics (CFD) method, the numerical simulation is verified on M6 wing. Physical Optics (PO) and Multilevel Fast Multipole Method (MLFMM) are chosen for numerical study on the stealthy performance of cylinder and a certain scale model of flying wing UAV. Moreover, the verified methods are applied to study the aerodynamic and stealthy characteristics of flying wing UAV. The results show that the aerodynamic and stealthy calculation result is close to the experiment data, indicating that the numerical simulation method is valid. Not only the longitudinal aerodynamic performance of flying wing UAV with fuselage leading edge similar to eagle mouth increases appreciably, but also its stealthy performance improves significantly in the forward direction with the azimuth angle from -25°～25°. In addition, it indicates that the stealthy inverse design method is effective. The design with leading edge similar to eagle mouth mainly affects the pressure distribution of fuselage, and it is helpful to advance the lift/drag characteristic. At the same time, the stealthy performance of the optimize design is better than the traditional blunt leading edge at different frequencies and rolling angles.

stealthy inverse design; flying wing UAV; similar to eagle mouth; aerodynamic; stealthy

10.11918/j.issn.0367-6234.201607022

V211.3

A

0367-6234(2017)10-0022-09

2016-07-07

國家自然科學基金(11302178)

張 樂(1988-)，男，博士，工程師；

周 洲(1966-)，女，教授，博士生導師

張 樂，568498886@qq.com

(編輯張 紅)