驅動力矩對汽車轉向驅動分岔的影響分析?

王憲彬，施樹明

(1.東北林業大學交通學院，哈爾濱 150040； 2.吉林大學交通學院，長春 130025)

驅動力矩對汽車轉向驅動分岔的影響分析?

王憲彬1，施樹明2

(1.東北林業大學交通學院，哈爾濱 150040； 2.吉林大學交通學院，長春 130025)

為研究驅動力矩對汽車動力學穩定性的影響，以引入驅動力矩的5自由度汽車二維非線性動力學模型為基礎，利用前輪轉角作為中間變量，建立了相應的7自由度自治系統模型，分析了不同驅動方式下，驅動力矩對汽車轉向驅動分岔的動力學特征的影響。以前輪驅動汽車為例，利用相空間、狀態變量時間序列、功率譜密度和李雅普諾夫指數分析了驅動力矩對轉向驅動分岔特征影響的動力學演變過程。結果表明：驅動力矩的大小將直接影響汽車動力學系統的分岔特征，在分析汽車的動力學分岔特征時應同時考慮前輪轉角和驅動力矩兩個分岔參數的影響。

汽車非線性動力學；驅動力矩；轉向驅動耦合工況；分岔；混沌

前言

汽車的動力學特征是研究汽車主動安全性的重要理論基礎。汽車作為典型的非線性動力學系統，在極限工況下很容易出現分岔或混沌等不穩定的動力學行為。隨著非線性動力學理論和輪胎力學的發展，由于輪胎側向力的非線性特征使汽車產生轉向分岔的動力學失穩機理已基本確認[1-3]。但是經典的2自由度模型假設縱向速度不變，且不考慮輪胎縱向力對系統穩定性的影響[4]。而汽車在轉向和驅動聯合工況中，隨著縱向速度的增大，輪胎所要提供的地面縱向驅動力也越大。輪胎在不同驅動條件下能夠提供的側向力不同。因此，忽略驅動力矩的轉向分岔機理，并不能完整揭示汽車在轉向和驅動聯合工況下的動力學分岔特征，也無法解釋驅動力矩對汽車轉向驅動分岔的影響。

在轉向分岔分析中最具有代表性的研究成果是文獻[5]中提出的車身側偏角及其變化率的相平面圖。文獻[6]和文獻[7]中的研究發現：汽車系統存在3個平衡點，一個是穩定的焦點，另外兩個是不穩定的鞍點；當車身側偏角增加到一定程度后，汽車的失穩主要是由鞍結分岔引起的。文獻[8]中分析了低附著系數路面上前輪轉角變化時引起的2自由度車輛系統的分岔現象。文獻[9]中分析了當前輪轉角變化時系統的3個平衡點在相平面上的變化，并得到了狀態變量隨前輪轉角變化的分岔圖。文獻[10]中利用幾何交點軌跡法研究汽車轉向動力學的穩定性時，同樣得到了相近的結論，即汽車轉向動力學系統存在3個平衡點：一個穩定的焦點和兩個不穩定的鞍點。文獻[11]中在2自由度模型的基礎上，將縱向速度引入車身模型，去除了縱向速度不變的假設，彌補了基于2自由度模型提出的穩定性判據的不足。文獻[12]中發現了汽車轉向運動的混沌現象，指出汽車轉向失穩的本質特征是汽車動力學系統的混沌運動。文獻[13]中借助達朗貝爾原理，提出了一種基于約束分岔和連續法的分析方法，建立了包含縱向速度、側向速度、橫擺角速度和側傾的汽車動力學模型，分析了制動減速度引起的分岔現象。文獻[14]中通過對經典的滑移率定義進行拓展，分析了失穩情況下的輪胎縱向滑移率方程的有效性，建立了引入驅動的5自由度汽車非線性模型，分析了不同前輪轉角輸入時，不同驅動方式對汽車操縱穩定性的影響。

綜上所述，以2自由度汽車動力學模型為基礎的汽車轉向穩定性研究已取得了豐碩的研究成果。引入縱向速度的3自由度模型揭示了汽車失穩的混沌運動本質特征。引入驅動的5自由度模型，揭示了不同驅動方式對汽車操縱穩定性的影響。但是，驅動力矩對汽車轉向驅動分岔特征的影響及其動力學演變過程仍缺少深入研究。

1 車輛系統模型

以3自由度車輛轉向系統模型[15]為基礎，引入包含驅動力矩的車輪動力學方程，5自由度的車輛動力學系統方程見式(1)。圖1為單軌車輛模型的示意圖。

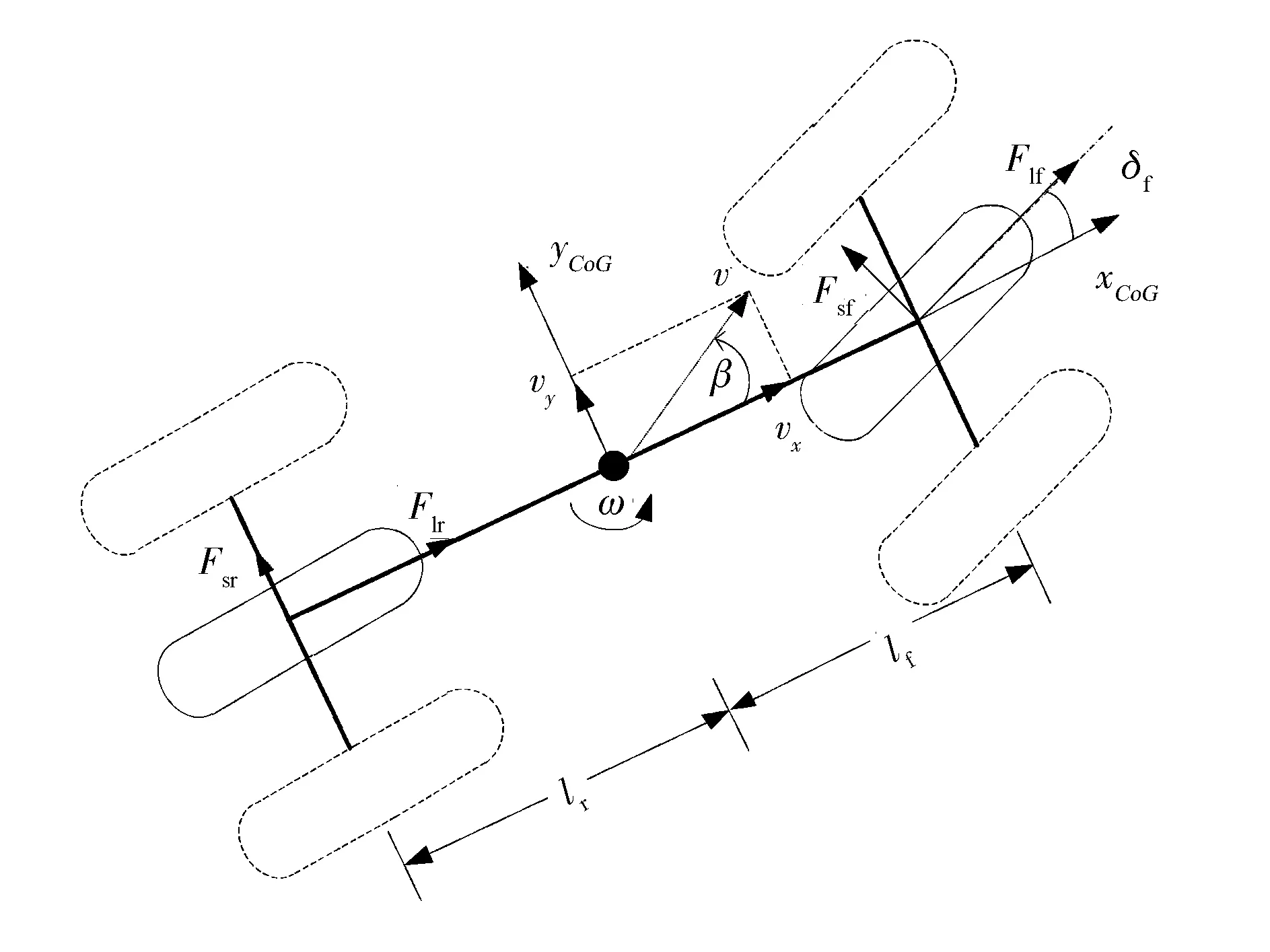
圖1 車輛系統單軌模型

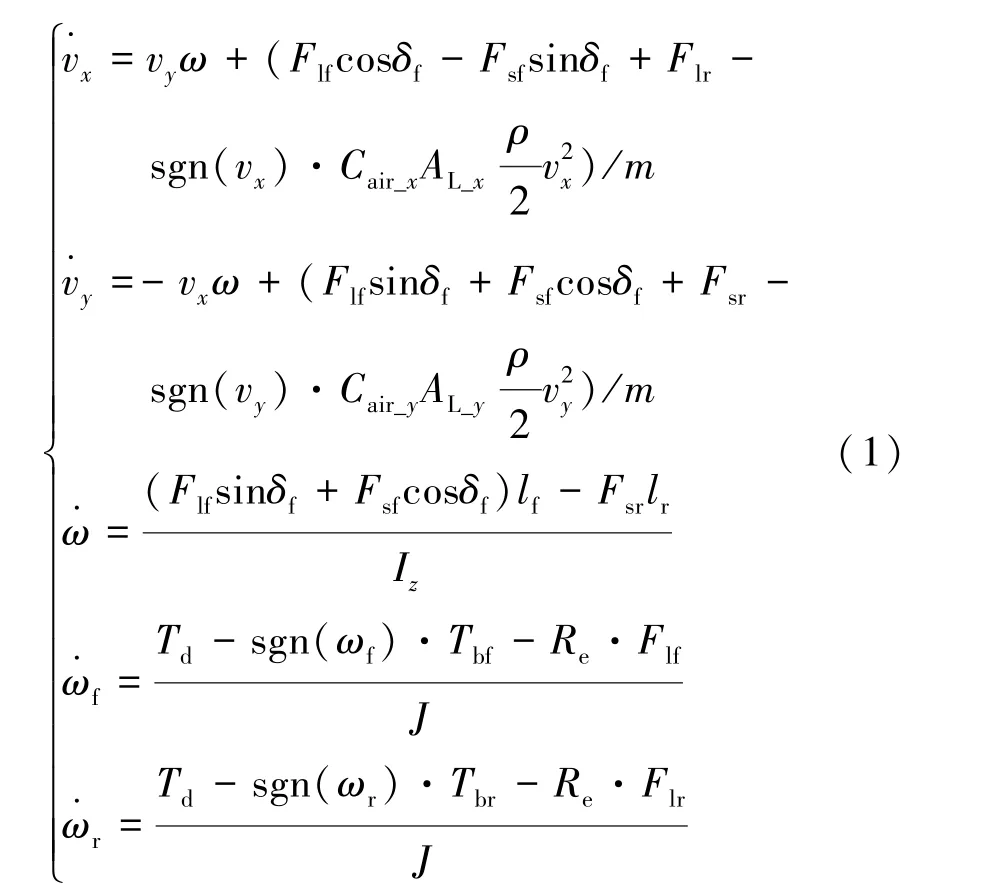
式中：m為整車質量；Iz為繞z軸的轉動慣量；vx為車輛坐標系質心處的縱向速度；vy為車輛坐標系質心處的側向速度；ω為車輛橫擺角速度；ωf為車輛前輪角速度；ωr為車輛后輪角速度；lf為車輛前輪到質心的距離；lr為車輛后輪到質心的距離；J為車輪的轉動慣量；δf為車輛前輪轉角；Cair_x，Cair_y為縱向和側向空氣阻力系數；AL_x，AL_y為車輛縱向和側向迎風面積；ρ為空氣密度；Td為驅動力矩；Tbf，Tbr為前、后輪制動力矩；Re為車輪滾動半徑；Flf，Flr，Fsf，Fsr為混合滑移狀態下，前、后車輪縱向力和側向力。

表1中給出了車輛系統模型中參數的取值。

表1 車輛參數

輪胎力的計算方法采用魔術公式[16]：

式中：B，C，D，E為參數；F為輪胎縱向力或側向力；x為輪胎滑移率或側偏角。

穩態滑移率公式[16]為

式中：ωw為車輪轉動角速度；vwx為車輪平面內，輪心處的縱向速度。

縱向輪胎力參數如表2所示。

表2 縱向輪胎力參數

前后輪的輪胎側偏角的表達式分別為

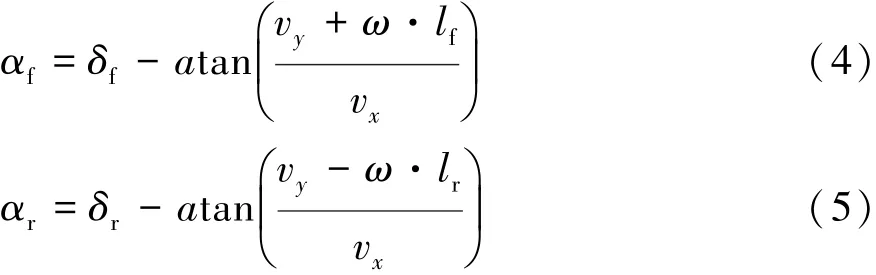
其中：δr＝0

表3為單軌車輛模型采用的側向輪胎力參數[9]。

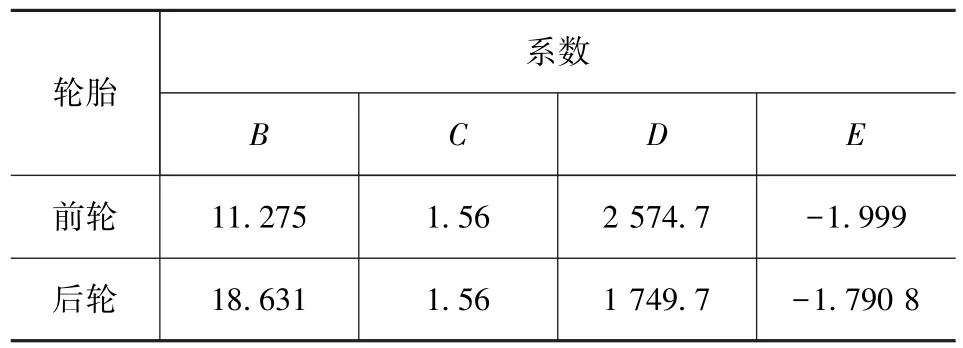
表3 側向輪胎力參數

輪胎混合滑移，采用Pacejka提出的模型進行分析，具體計算步驟按照式(6)進行[16]。

式中：Flf0，Flr0，Fsf0，Fsr0為穩態下前后車輪縱向力和側向力，其大小可用式(2)計算；Gx，Gy為輪胎力混合滑移修正函數；rx，1，rx，2，ry，1，ry，2為輪胎力混合滑移修正系數，見表4。

表4 混合滑移系數

2 驅動力矩對分岔特征的影響

2.1 自治系統模型轉化

選用典型汽車操縱穩定性試驗條件，蛇行工況作為試驗條件。為配合蛇行工況試驗，輸入的前輪轉角按正弦規律變化：

式中：A為前輪轉角的幅值；ωsf為前輪轉角的角頻率。將前輪轉角公式導入5自由度的汽車動力學模型，系統方程寫成狀態方程的形式：

其中：X＝(vy，ω，vx，ωf，ωr，δf，z)

式中：z為中間變量。為便于分析，通常將動力學方程改寫為自治方程形式。聯立式(7)～式(9)，則5自由度汽車動力學方程(式(1))的7自由度的自治方程為

2.2 驅動力矩對分岔特征的影響

試驗的縱向速度初值vx＝20m/s。驅動輪上施加的驅動力矩Td的取值范圍為0.2～140N·m，每測點其增量為0.2N·m。固定前輪轉角幅值 A＝0.03rad，前輪轉角變化頻率為f＝0.4Hz，其角頻率為ωsf＝2π·0.4＝0.8π。

圖2～圖4分別給出了縱向速度初值vx＝20m/s時，前輪驅動系統的側向速度vy、橫擺角速度ω和縱向速度vx的分岔圖。

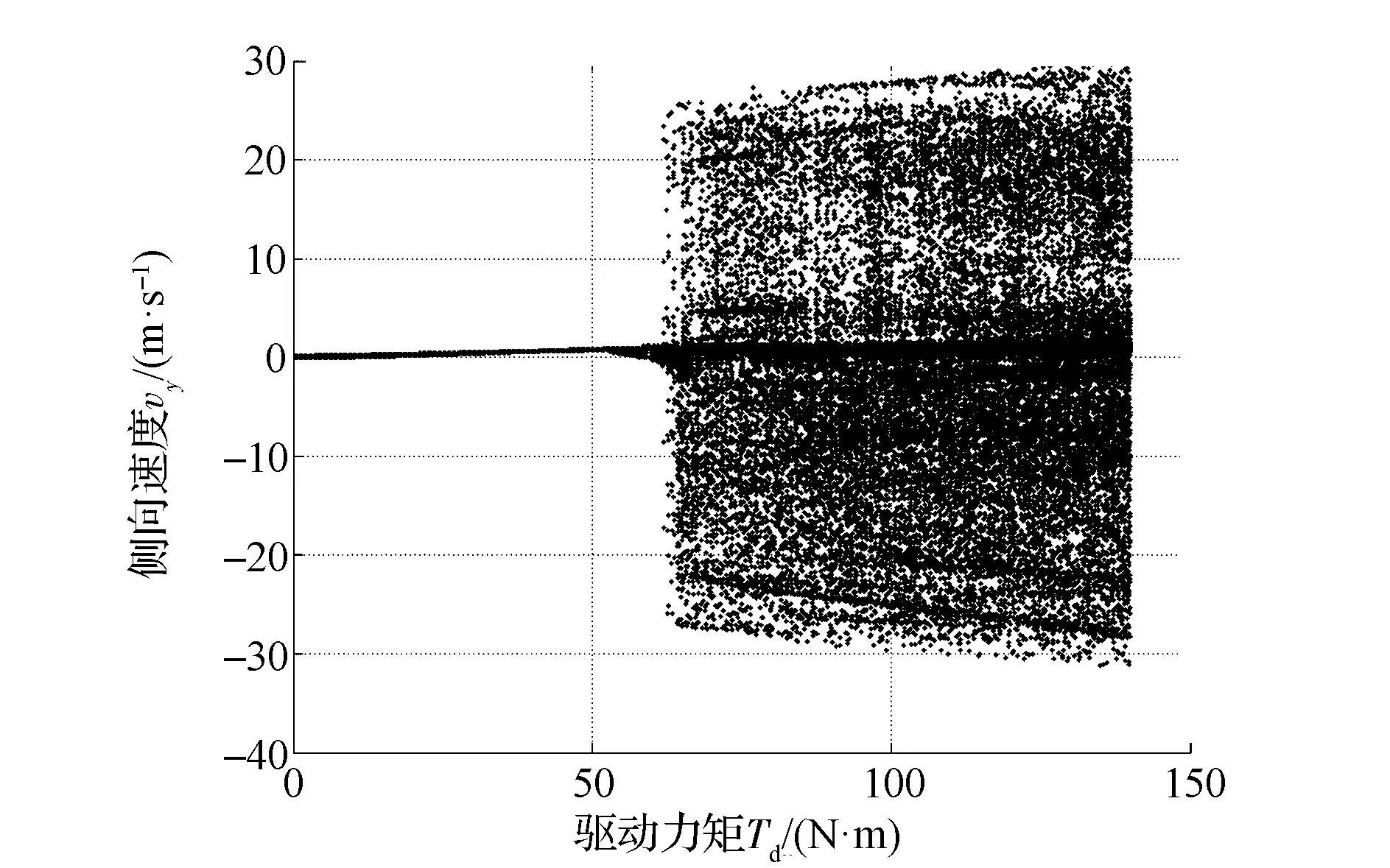
圖2 側向速度vy的分岔圖(A ＝0.03rad，vx＝20m/s，前驅)

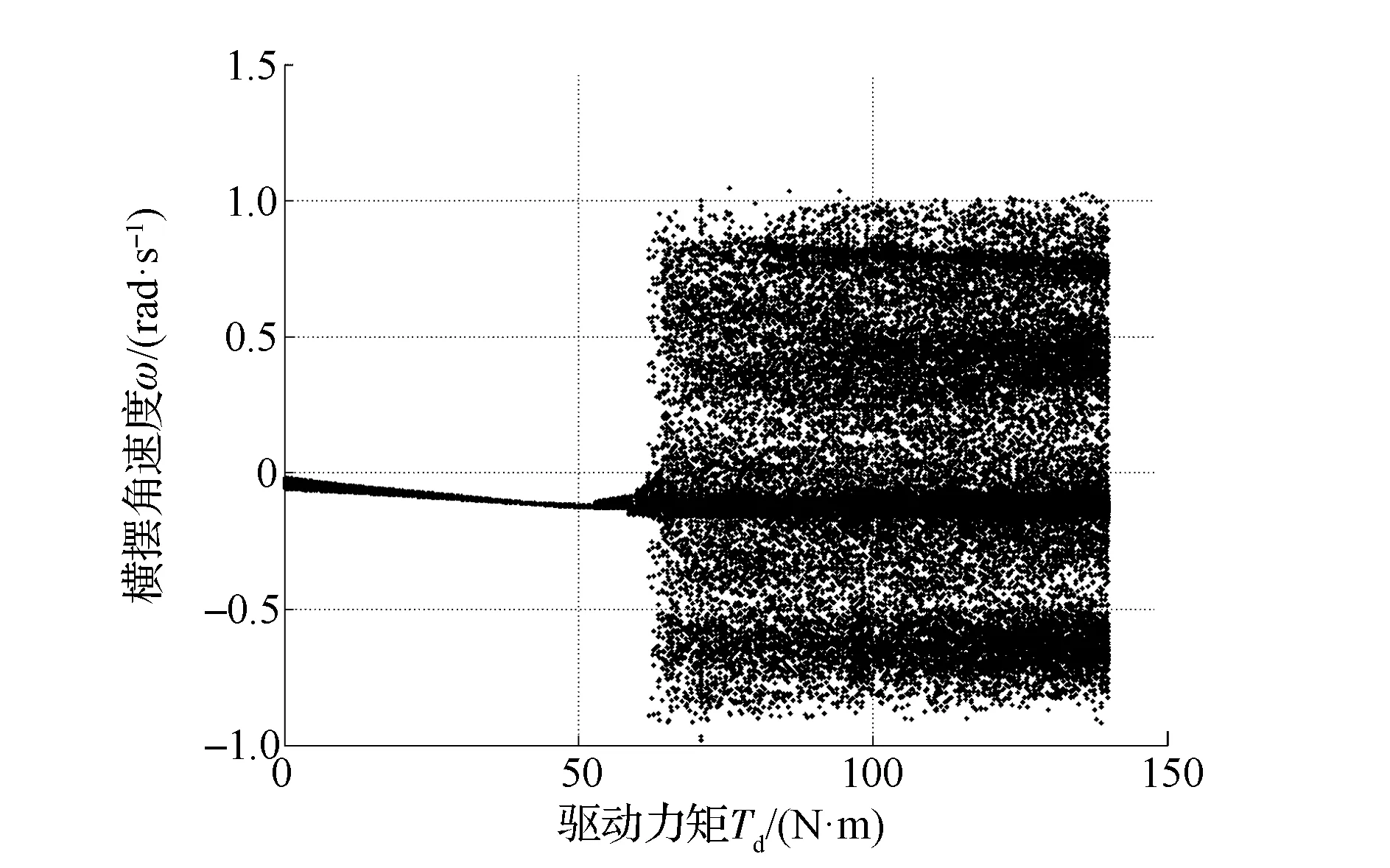
圖3 橫擺角速度ω的分岔圖(A ＝0.03rad，vx＝20m/s，前驅)

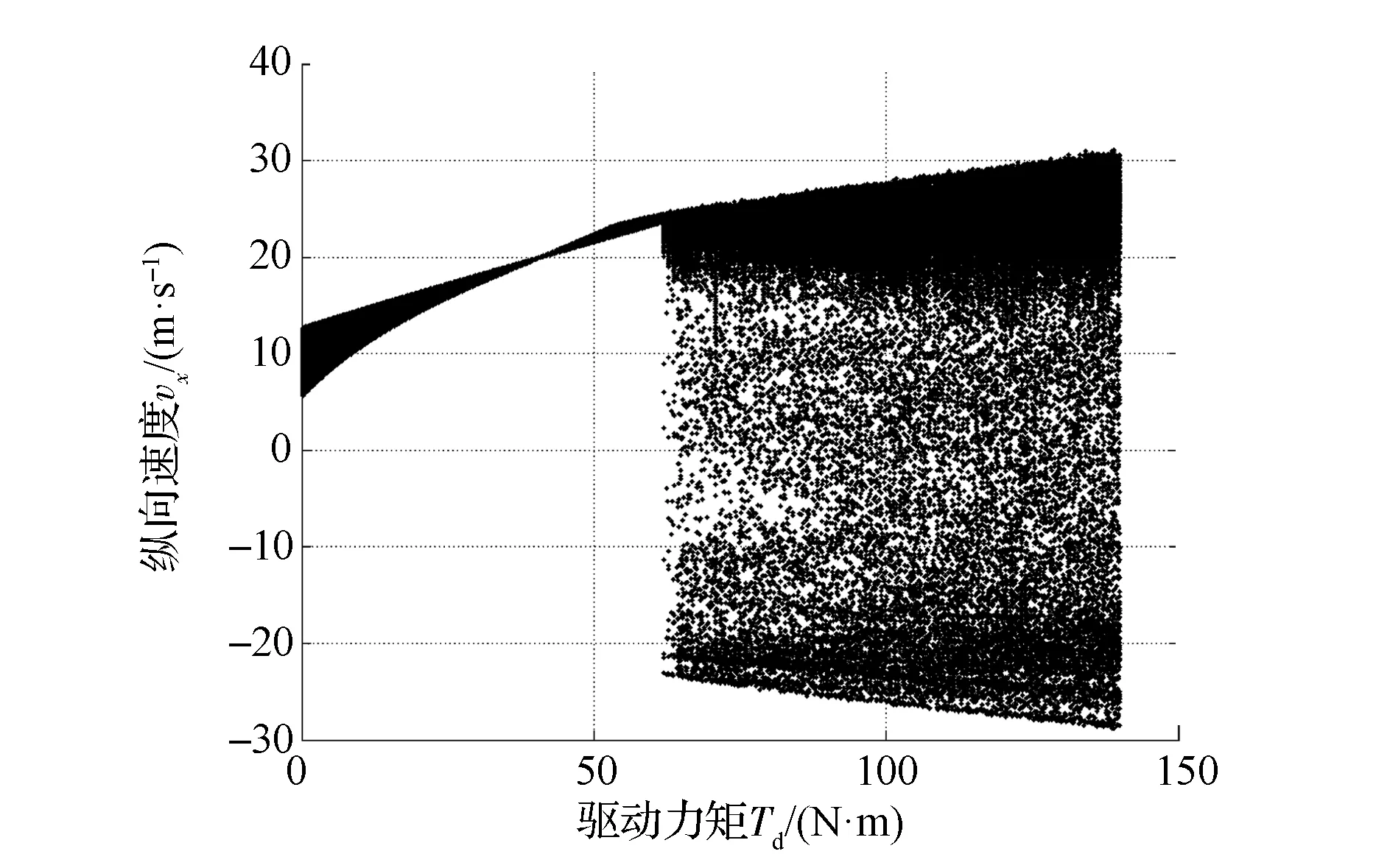
圖4 縱向速度vx的分岔圖(A ＝0.03rad，vx＝20m/s，前驅)

分岔圖的做法如下：對于給定的前輪轉角幅值A＝0.03rad和每一驅動力矩Td，當t＝0時，給定系統初值 vx＝20m/s，vy＝0，ω ＝0，ωf＝0，ωr＝0時，用MATLAB求解系統7自由度汽車動力學方程，得到系統的狀態變量隨時間的變化值。經過狀態變量瞬態變化后，在一定時間內(仿真總時長TS＝200s)對狀態變量按一定的時間頻率(本節中f＝0.4Hz)進行采樣，所有采樣點的狀態變量的取值對應驅動力矩Td的大小，在相應的變化范圍內構成了汽車系統狀態變量隨驅動力矩的分岔圖。

由分岔圖可以看出如下情形。

(1)當驅動力矩Td＜62N·m時，側向速度vy的值域范圍隨著驅動力矩Td的增大而逐漸增大，當Td＝61.8N·m時，最終 vy的值域范圍達到[-0.827 7，0.925 5]m/s。而橫擺角速度ω則隨著驅動力矩Td的增大先逐漸減小后增大，當Td＝61.8N·m時，ω的值域范圍為[-0.129，-0.008 681]rad/s。當驅動力矩Td＜62N·m時，在仿真的初始階段由于驅動力小于空氣阻力，使得縱向速度vx在驅動力矩的作用下不斷減小。隨著驅動力矩Td的增大，縱向速度的值域變化范圍出現了由大變小、再變大的過程。

(2)當驅動力矩Td＝62N·m時，側向速度vy的值域范圍突然增大到[-17.28，23.44]m/s，隨著驅動力矩的增大而逐漸增大，當Td＝140N·m時，最終vy的值域范圍達到約[-30，30]m/s。當驅動力矩Td＝62N·m時，橫擺角速度ω的值域范圍也發生了突變，增大到[-0.890 3，0.820 2]m/s。此后隨著驅動力矩的增大其值域范圍變化較為穩定，當Td＝140N·m時，ω的值域范圍為[-0.826 6，0.893 7]rad/s。當驅動力矩Td＝62N·m時，縱向速度vx的值域范圍也突然增大，約為[-23.01，24.49]m/s。隨著驅動力矩的增大，vx的值域范圍逐漸增大，當Td＝140N·m 時，vx的值域范圍為[-28.53，30.55]m/s。

圖5和圖6分別為全輪驅動和后輪驅動系統的狀態變量分岔圖。

由圖可見：全輪驅動、后輪驅動的分岔圖與前輪驅動的分岔圖的整體趨勢相近，其中橫擺角速度的分岔圖中橫擺角速度的值域范圍有所擴大；對應的分岔參數驅動力矩在不同驅動方式時明顯不同，全輪驅動系統發生分岔時的驅動力矩由前輪驅動時的Td＝62N·m減小到Td＝57.4N·m，而后輪驅動對應的驅動力矩僅為Td＝53.6N·m；不同驅動方式對應的分岔參數的大小順序為前輪驅動(Td＝62N·m)＞全輪驅動(Td＝57.4N·m)＞后輪驅動(Td＝53.6N·m)。

圖7～圖9給出了前輪轉角幅值A＝0.02rad，縱向速度初值vx＝30m/s時，前輪驅動、全輪驅動和后輪驅動系統的狀態變量分岔圖。

圖5 狀態變量的分岔圖(A＝0.03rad，vx＝20m/s，全驅)

圖6 狀態變量的分岔圖(A＝0.03rad，vx＝20m/s，后驅)

圖7 狀態變量的分岔圖(A＝0.02rad，vx＝30m/s，前驅)

圖8 狀態變量的分岔圖(A＝0.02rad，vx＝30m/s，全驅)

由圖中見：這些分岔圖的整體趨勢與前輪轉角幅值A＝0.03rad、縱向速度初值vx＝20m/s時的分岔圖的一致；但對應的分岔參數驅動力矩Td發生了相應的變化，前輪、全輪和后輪驅動系統對應的驅動力矩Td分別為134.6，105.6和60.4N·m；分岔參數驅動力矩Td在不同驅動方式時的大小對應順序沒有變化，依然為前輪驅動(Td＝134.6N·m)＞全輪驅動(Td＝105.6N·m)＞后輪驅動(Td＝60.4N·m)。

由此可見，不同驅動方式下，驅動力矩對汽車系統動力學分岔特征產生的影響不同。

圖9 狀態變量的分岔圖(A＝0.02rad，vx＝30m/s，后驅)

3 分岔特征的動力學演變過程

從動力學本質上說，5自由度汽車動力學系統的分岔現象可以歸結為：在周期轉角激勵的作用下，隨著驅動力矩的增大，5自由度汽車系統將由準周期運動過渡到混沌。

不失一般性地，本節僅對前輪驅動系統的動力學演變過程進行分析，仿真分析條件具體為：在每一恒定驅動力矩加速條件下，在前輪上施加定周期的正弦轉角。

具體試驗參數為：縱向速度初值 vx＝20m/s，vy＝ 0，ω ＝0，ωf＝0，ωr＝0，在前輪上施加恒定驅動力矩(即驅動模式為前驅)，驅動力矩Td分別取值為20，62，63 和 100N·m，前輪轉角幅值 A ＝0.03rad，前輪轉角變化的頻率為f＝0.4Hz，其角頻率ωsf＝2π·0.4＝0.8π。

3.1 驅動力矩Td＝20N·m

圖10～圖16給出了Td＝20N·m時的數值計算結果。

圖10為系統狀態變量vx-vy-ω相空間內的相軌跡。由圖可見：當Td＝20N·m時，系統的相軌跡為準周期環面。在整個仿真周期內，縱向速度vx由初始值開始逐漸增大，并穩定在一定范圍內，側向速度vy和橫擺角速度ω的絕對值由初始值開始周期振蕩，并最終穩定在一定范圍內。

由圖11和圖12中的狀態變量的時間序列也可得到與上述相同的結論。

圖10 vx-vy-ω相空間內的相軌跡(T d＝20N·m)

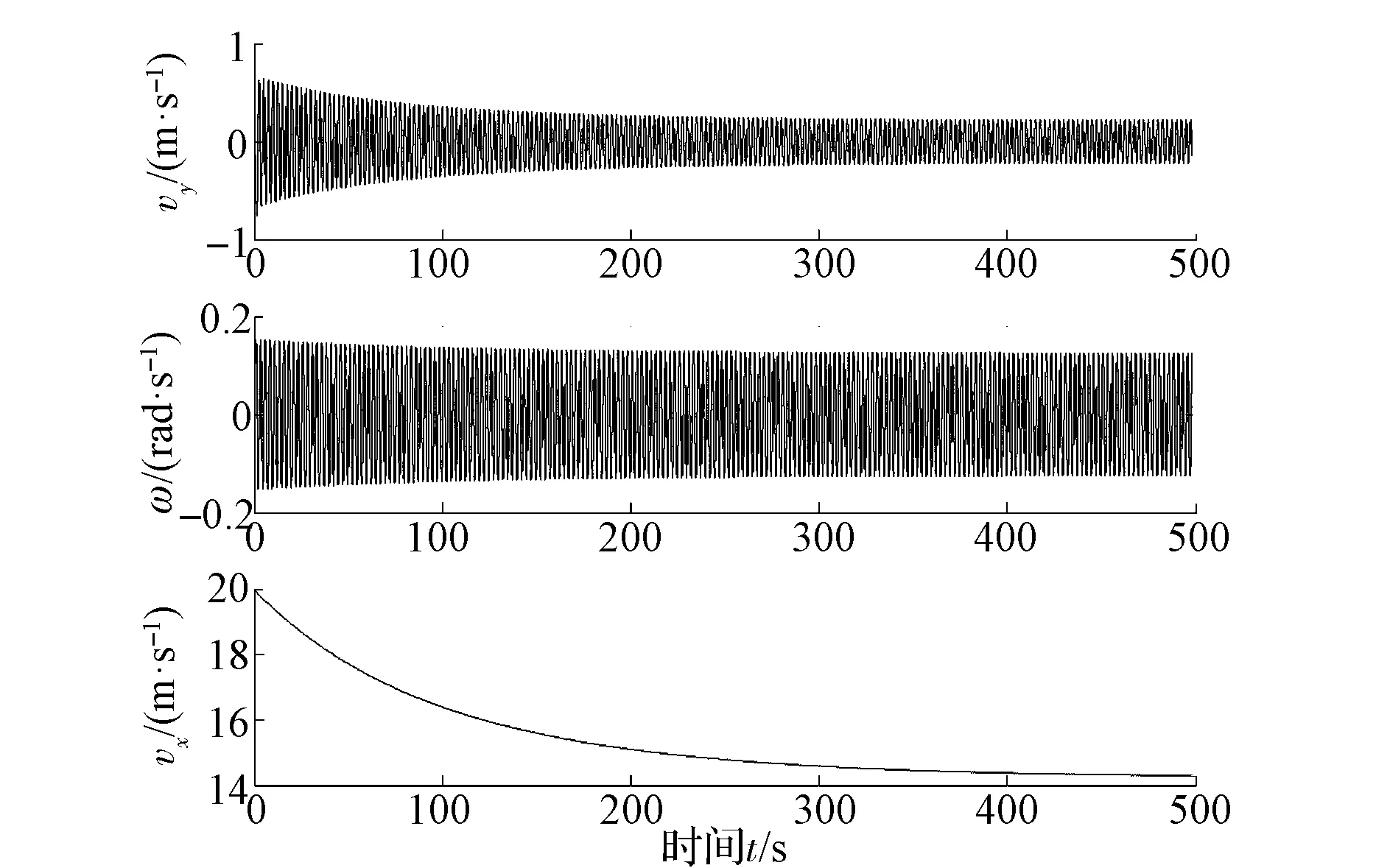
圖 11 狀態變量 (vx，vy，ω) 時間序列(T d＝20N·m)

圖 12 狀態變量 (vx，vy，ω) 時間序列局部(T d＝20N·m)

圖13為按前輪轉角的周期取值的相軌跡的龐 加萊截面圖。由圖可見，各個狀態變量的截面圖呈直線分布，這是典型的準周期運動的特征。

圖13 龐加萊截面(T d＝20N·m)

圖14 為各個狀態變量的功率譜密度圖。由圖可見：各個狀態變量的功率譜密度均呈典型的周期或準周期運動的單峰值分布特征；特別的，側向速度vy的變化頻率與前輪轉角輸入的變化頻率一致，約為0.4Hz。

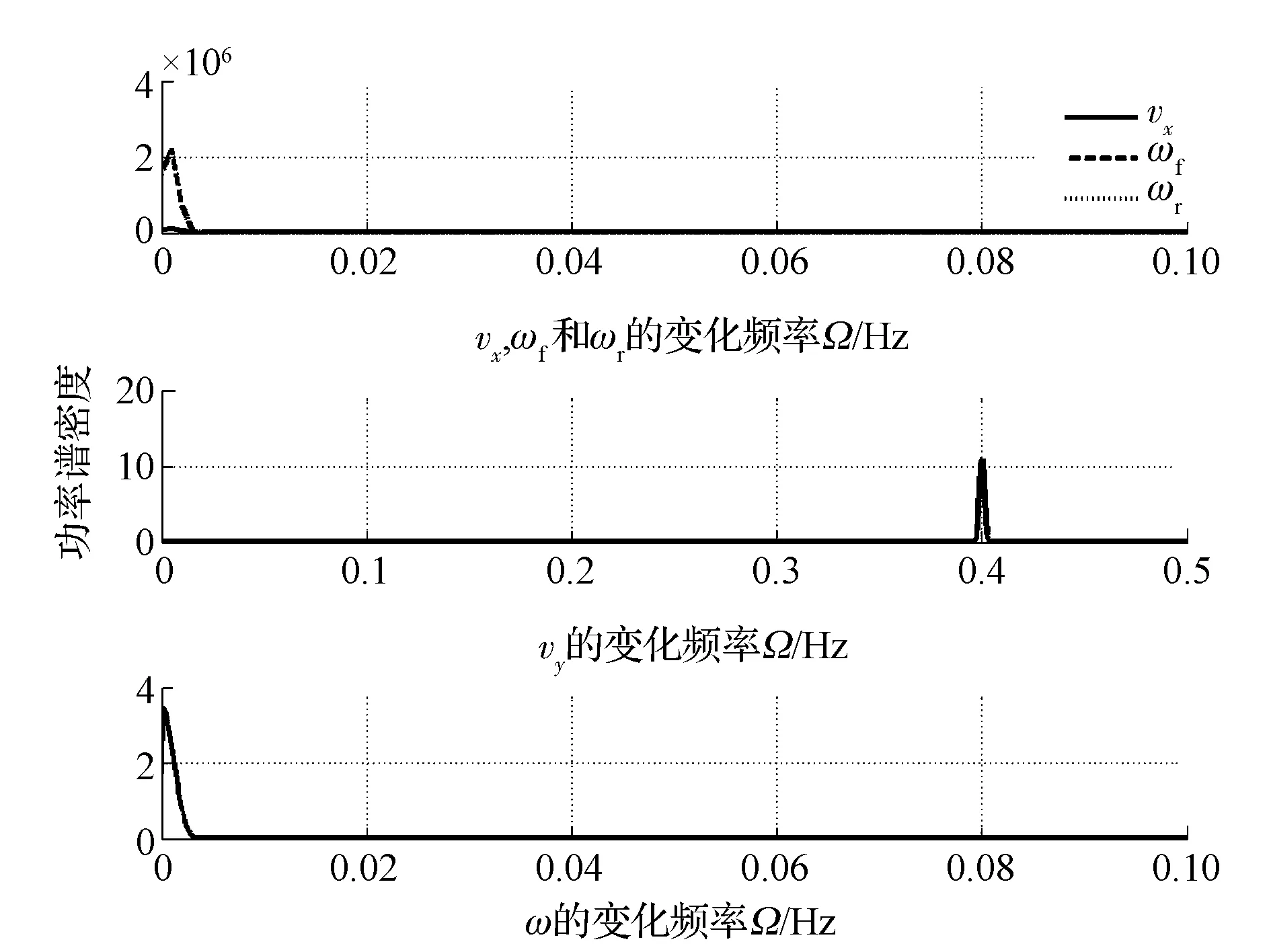
圖14 功率譜密度(T d＝20N·m)

圖15 和圖16均為系統狀態變量的李雅普諾夫指數。由圖可見，此時系統的李雅普諾夫指數譜為(0，0，0，-，-，-，-)，這證明系統處于非混沌的狀態。

圖15 李雅普諾夫指數(T d＝20N·m)

3.2 驅動力矩Td＝62N·m和Td＝63N·m

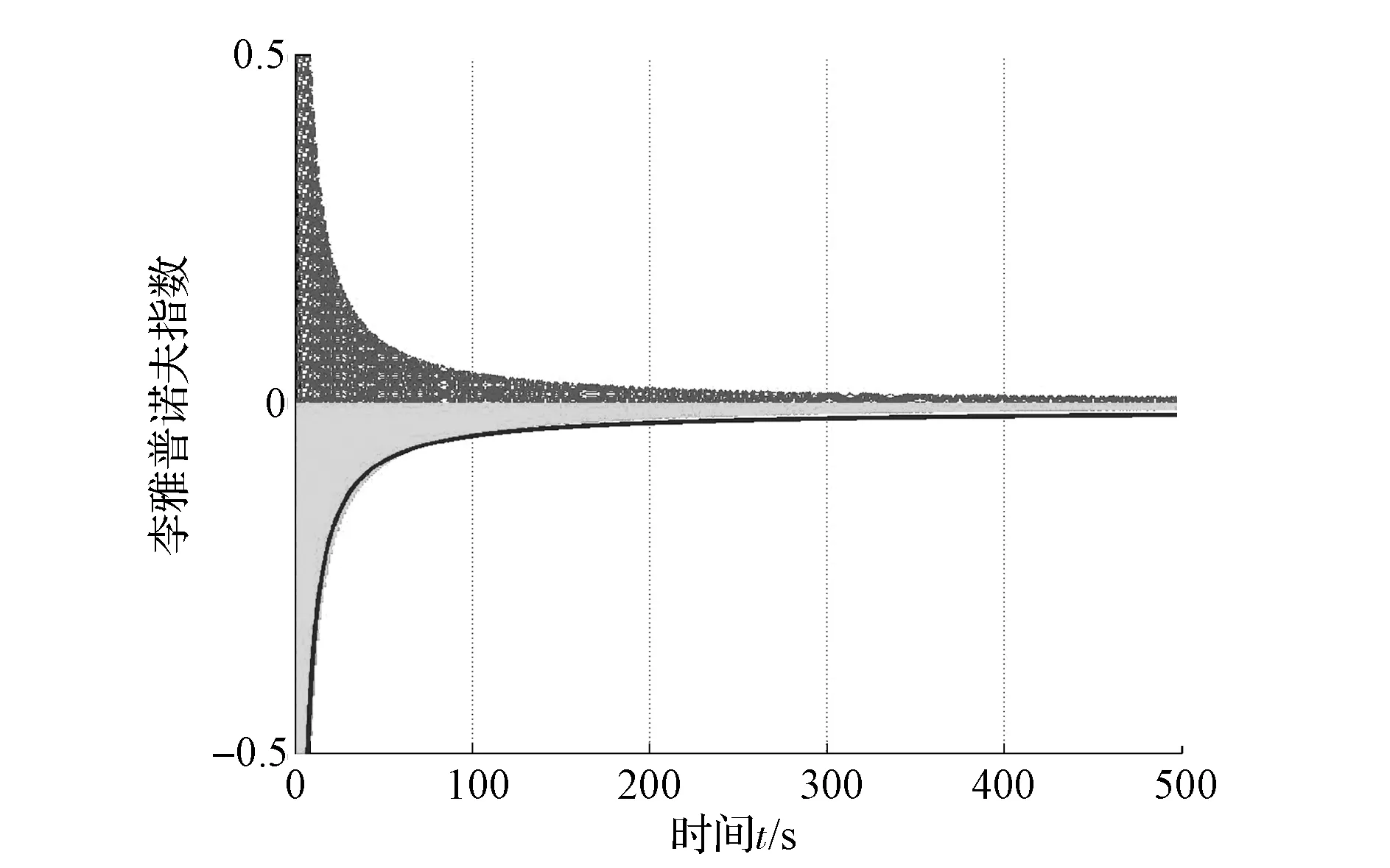
圖16 李雅普諾夫指數(T d＝20N·m)

圖17 ～圖23給出了Td＝62N·m時的數值計算結果。由上一節的分岔圖分析可知，此時系統的動力學特征發生了分岔，但分岔圖中狀態變量的結果點較為稀疏。

圖17為系統狀態變量vx-vy-ω相空間內的相軌跡。與Td＝20N·m時的相軌跡相比，系統的相軌跡由準周期環面開始逐漸破裂。

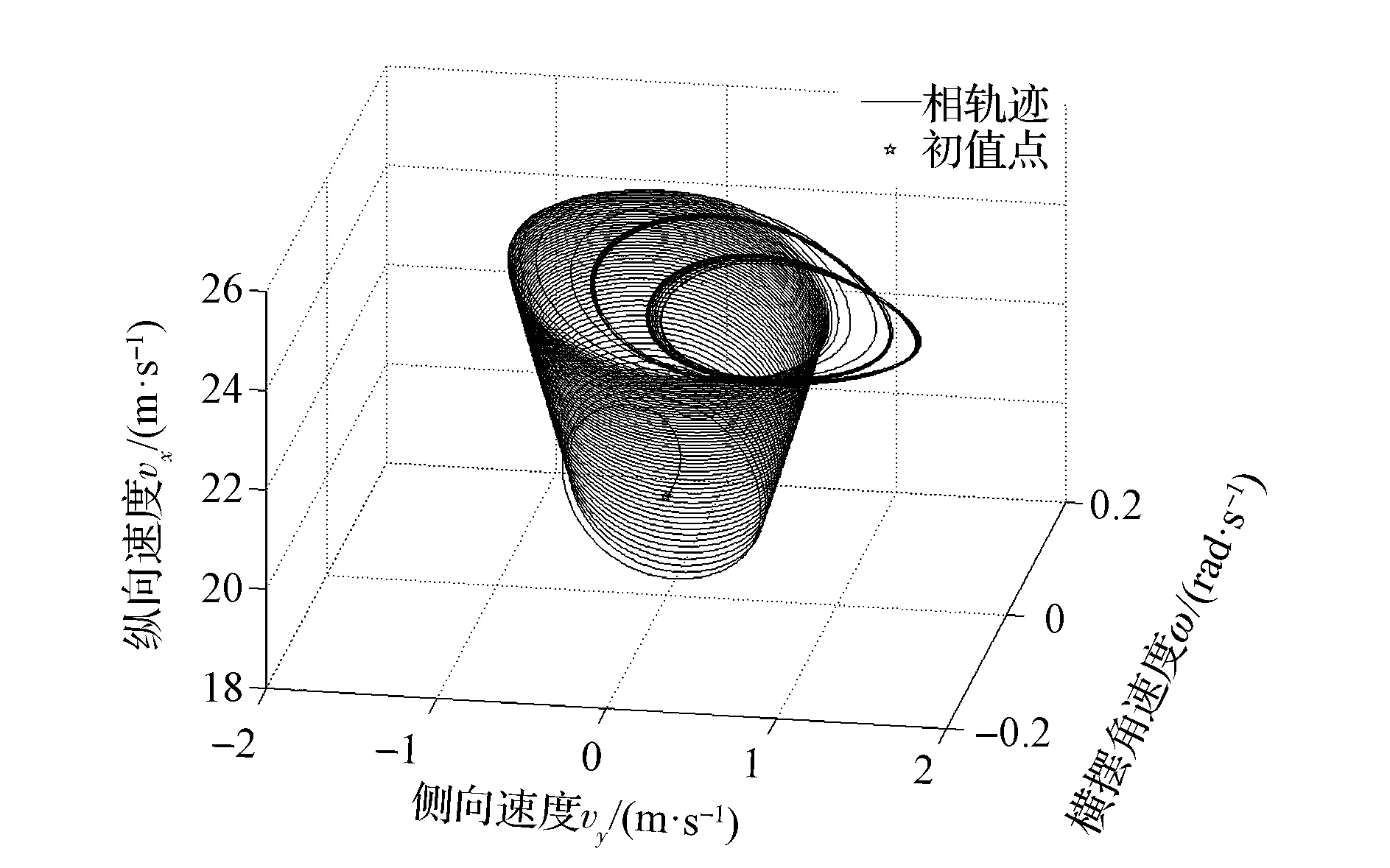
圖17 vx-vy-ω相空間內的相軌跡(T d＝62N·m)

由圖18和圖19可見：隨著驅動力矩的增大，系統的狀態變量盡管開始出現不穩定的趨勢，但最終仍然恢復了穩定狀態，其原因可能是由于驅動力矩Td＝62N·m較大，使系統處于加速狀態，在加速過程中系統出現了短暫的不穩定狀態；但系統縱向速度、側向速度和橫擺角速度之間的耦合，又使系統進入了另一個相對穩定的運動狀態，如在初始階段縱向速度不斷增加，側向速度和橫擺角速度的變化范圍也不斷加大，而當t＝145s時，縱向速度開始穩定在vx＝24.2m/s，并出現周期波動，側向速度和橫擺角速度的變化范圍也隨之減小。

圖18 狀態變量 (vx，vy，ω)時間歷程(T d＝62N·m)

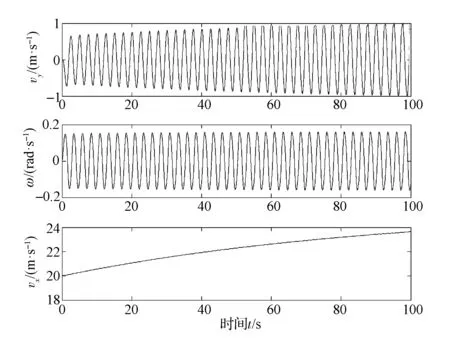
圖19 狀態變量 (vx，vy，ω) 時間歷程局部(T d＝62N·m)

與Td＝20N·m時系統的龐加萊截面圖相比，圖20中的龐加萊截面顯示：當驅動力矩達到Td＝62N·m時，系統的龐加萊截面已由直線分布過渡到了有限點集。

圖20 龐加萊截面(T d＝62N·m)

同時，圖21中的側向速度的功率譜密度也開始出現了寬頻多峰的特征。而圖22和圖23中的李雅普諾夫指數結果顯示，在仿真過程中系統體現出了一定的混沌特征，但最終又恢復到穩定狀態。即在仿真的初始階段系統的李雅普諾夫指數譜為(0，0，0，-，-，-，-)，當 t＝195s時，李雅普諾夫指數譜為(+，0，0，-，-，-，-)，說明系統存在混沌特征，當 t＝320s時，李雅普諾夫指數譜為(0，0，-，-，-，-，-)，說明系統的混沌特征消失，并最終保持到仿真結束(TS＝500s)。這與狀態變量時間序列的分析結果一致，即系統出現了短暫的不穩定狀態。綜上所述，當驅動力矩Td＝62N·m時，5自由度汽車系統的分岔特征有所體現但不明顯。

圖21 功率譜密度(T d＝62N·m)

圖22 李雅普諾夫指數(T d＝62N·m)

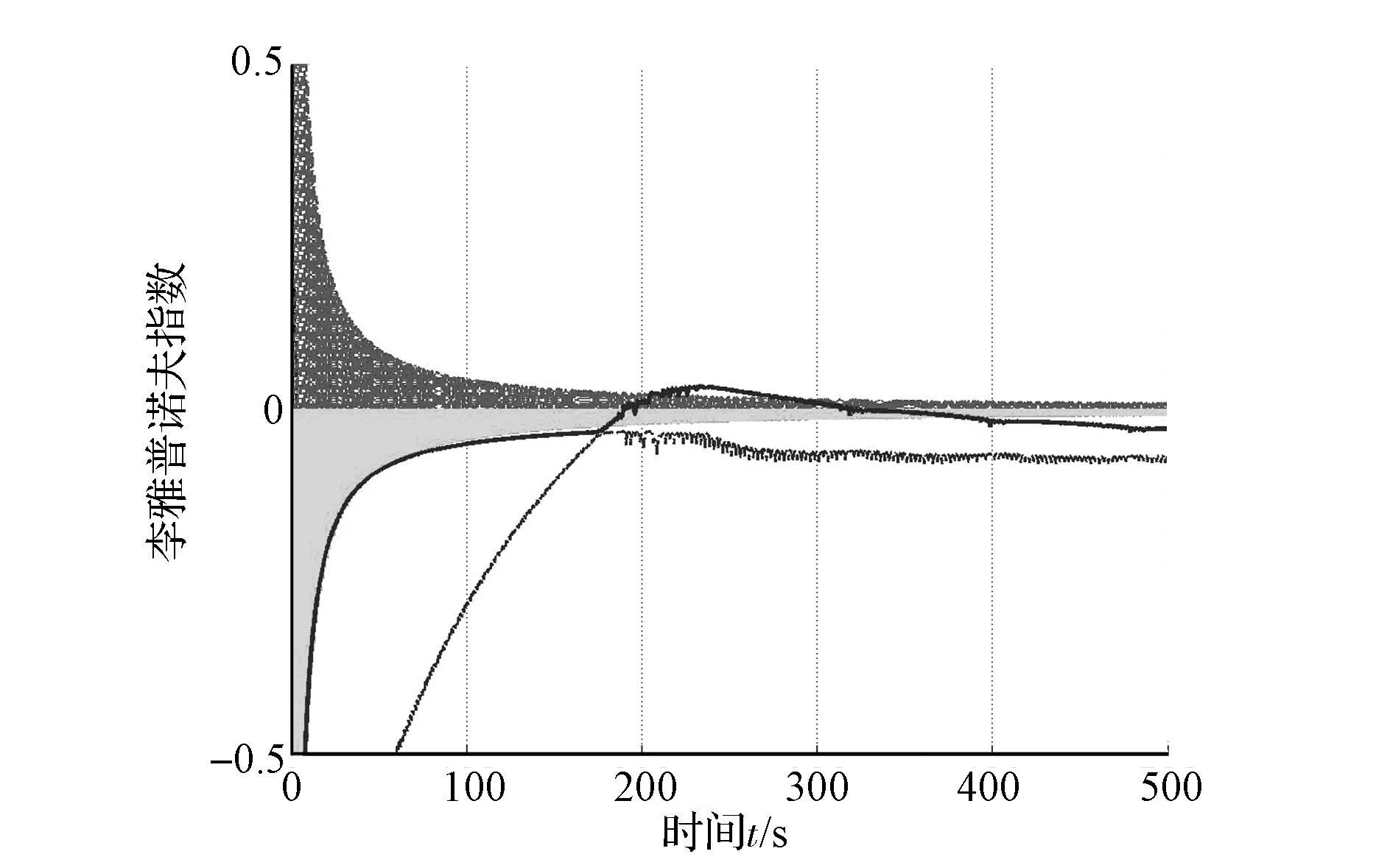
圖23 李雅普諾夫指數(T d＝62N·m)

延續上述分析，圖24～圖30給出驅動力矩Td＝63N·m時的分析結果。

圖24為系統狀態變量vx-vy-ω相空間內的相軌跡。由圖可見，與Td＝62N·m時的相軌跡相比，系統的相軌跡由準周期環面開始破裂并出現了混沌。

圖24 vx-vy-ω相空間內的相軌跡(T d＝63N·m)

由圖25和圖26可見：隨著驅動力矩的增大，系統的狀態變量在仿真過程中出現了不穩定的趨勢，最終恢復了穩定狀態，但與Td＝62N·m時的狀態變量相比，縱向速度、側向速度和橫擺角速度出現了劇烈變化，已經體現出了明顯的混沌特征，如果在實際行駛過程中出現類似的工況，駕駛員已無法駕馭汽車，將發生嚴重的交通事故。

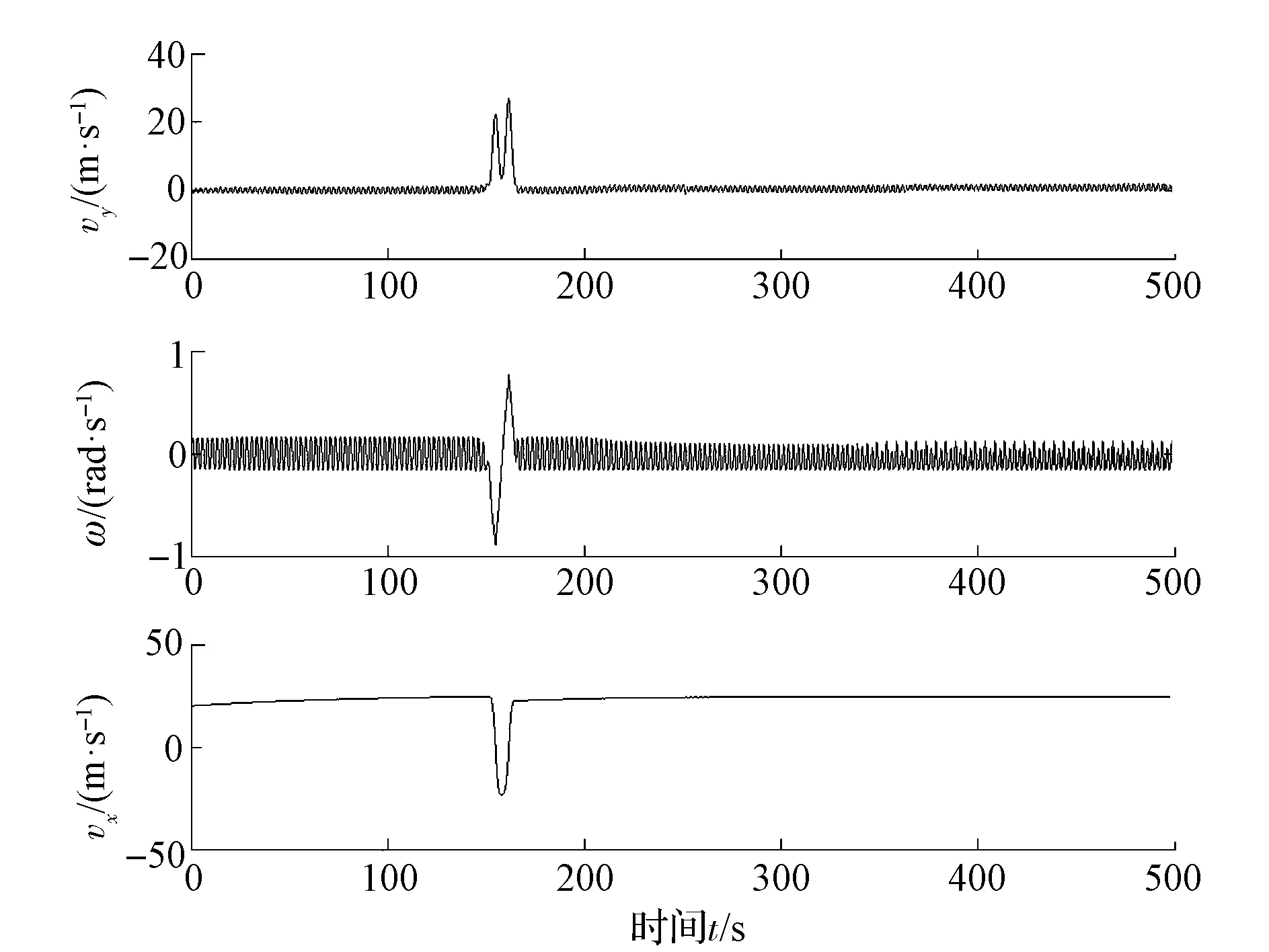
圖25 狀態變量 (vx，vy，ω)時間歷程(T d＝63N·m)

與Td＝62N·m時系統的龐加萊截面圖相比，圖27中的龐加萊截面顯示：當驅動力矩達到Td＝63N·m時，系統的龐加萊截面的有限點集的分布更為復雜。

圖27 龐加萊截面(T d＝63N·m)

圖28 中的側向速度的功率譜密度也同樣出現了寬頻多峰的特征。而圖29和圖30中的李雅普諾夫指數結果顯示，在仿真過程中系統體現出了較為明顯的混沌特征，即在仿真的初始階段系統的李雅普諾夫指數譜為(0，0，0，-，-，-，-)，當仿真時間 t＝180s時，李雅普諾夫指數譜為(+，0，0，-，-，-，-)，正的李雅普諾夫指數說明系統存在混沌特征，并最終保持到仿真結束(TS＝500s)。

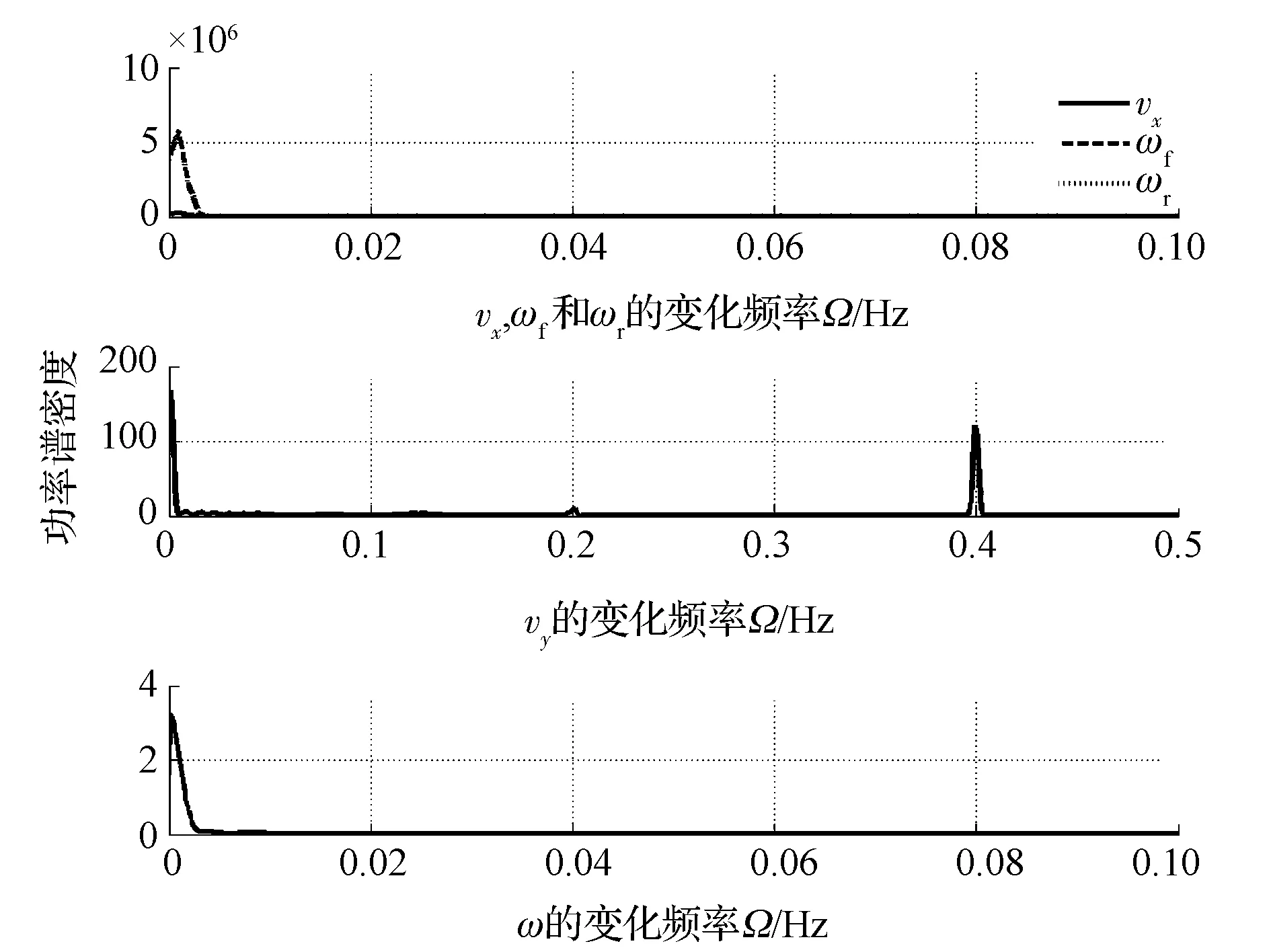
圖28 功率譜密度(T d＝63N·m)

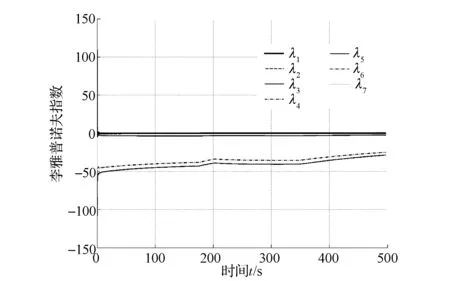
圖29 李雅普諾夫指數(T d＝63N·m)

圖30 李雅普諾夫指數(T d＝63N·m)

3.3 驅動力矩Td＝100N·m

圖31～圖37給出驅動力矩Td＝100N·m時的分析結果。由前面分岔圖的分析結果可知，此時系統已完全進入混沌狀態。

由圖31可見：系統的相軌跡由準周期環面開始破裂并出現了混沌。

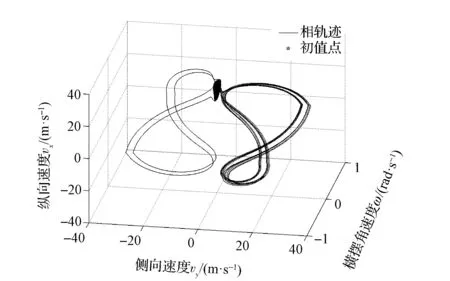
圖31 vx-vy-ω相空間內的相軌跡(T d＝100N·m)

同樣的，由圖32和圖33可見：當驅動力矩增大到Td＝100N·m時，狀態變量出現了連續的振蕩，這表示系統已失去穩定性，進入了混沌狀態。

圖32 狀態變量 (vx，vy，ω)時間歷程(T d＝100N·m)

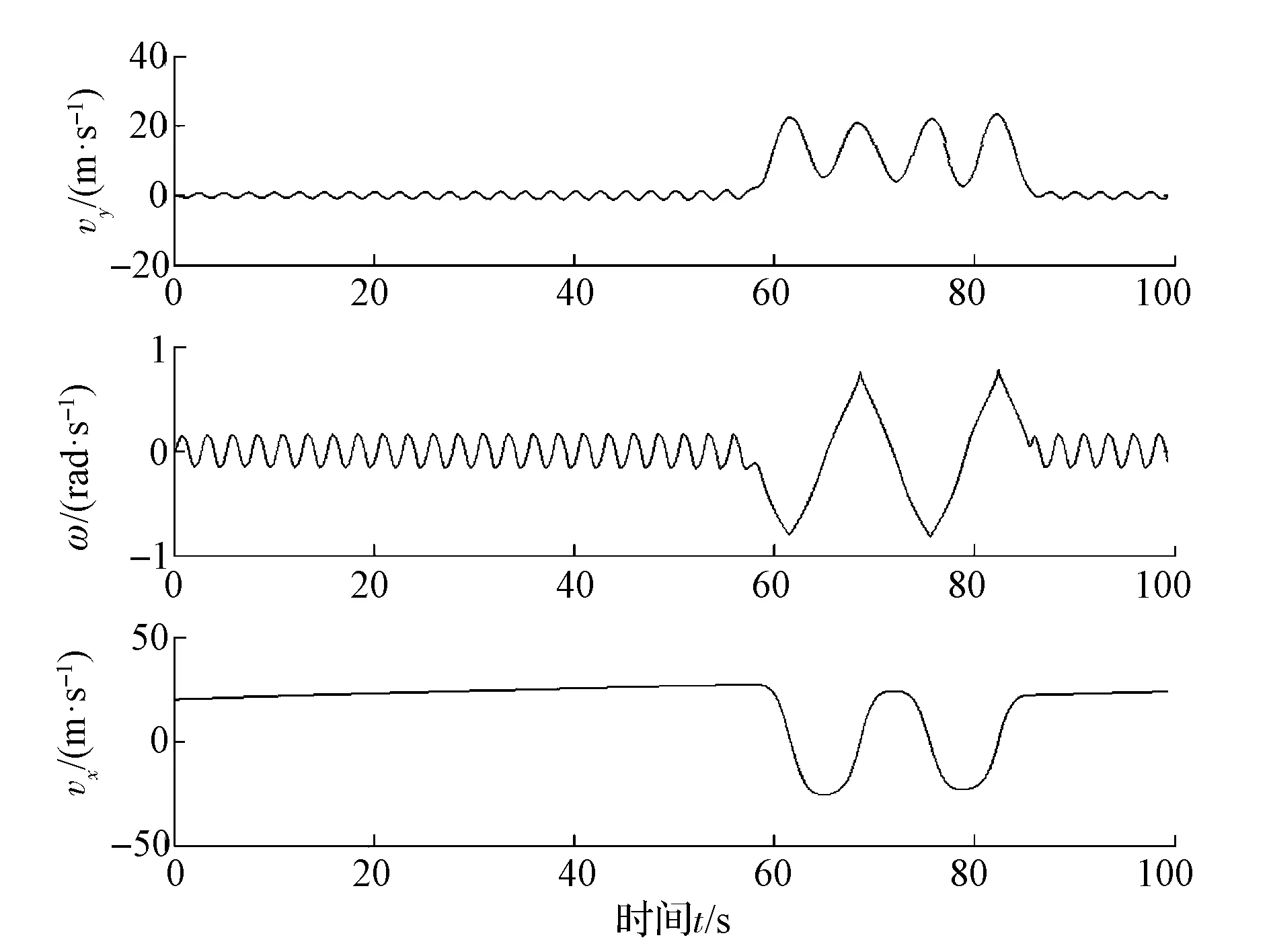
圖33 狀態變量 (vx，vy，ω) 時間歷程局部(T d＝100N·m)

而圖34中龐加萊截面的有限點集，圖35中各個狀態變量功率譜密度的寬頻多峰特征以及圖36和圖37中的正的李雅普諾夫指數，均表明系統存在混沌特征，這與分岔圖的分析保持一致。

圖34 龐加萊截面(T d＝100N·m)

圖35 功率譜密度(T d＝100N·m)

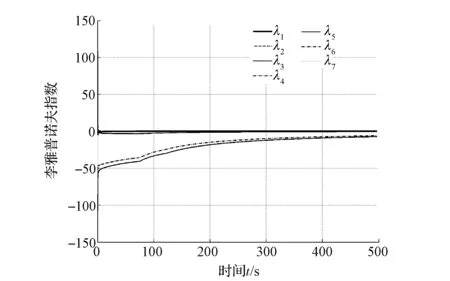
圖36 李雅普諾夫指數(T d＝100N·m)

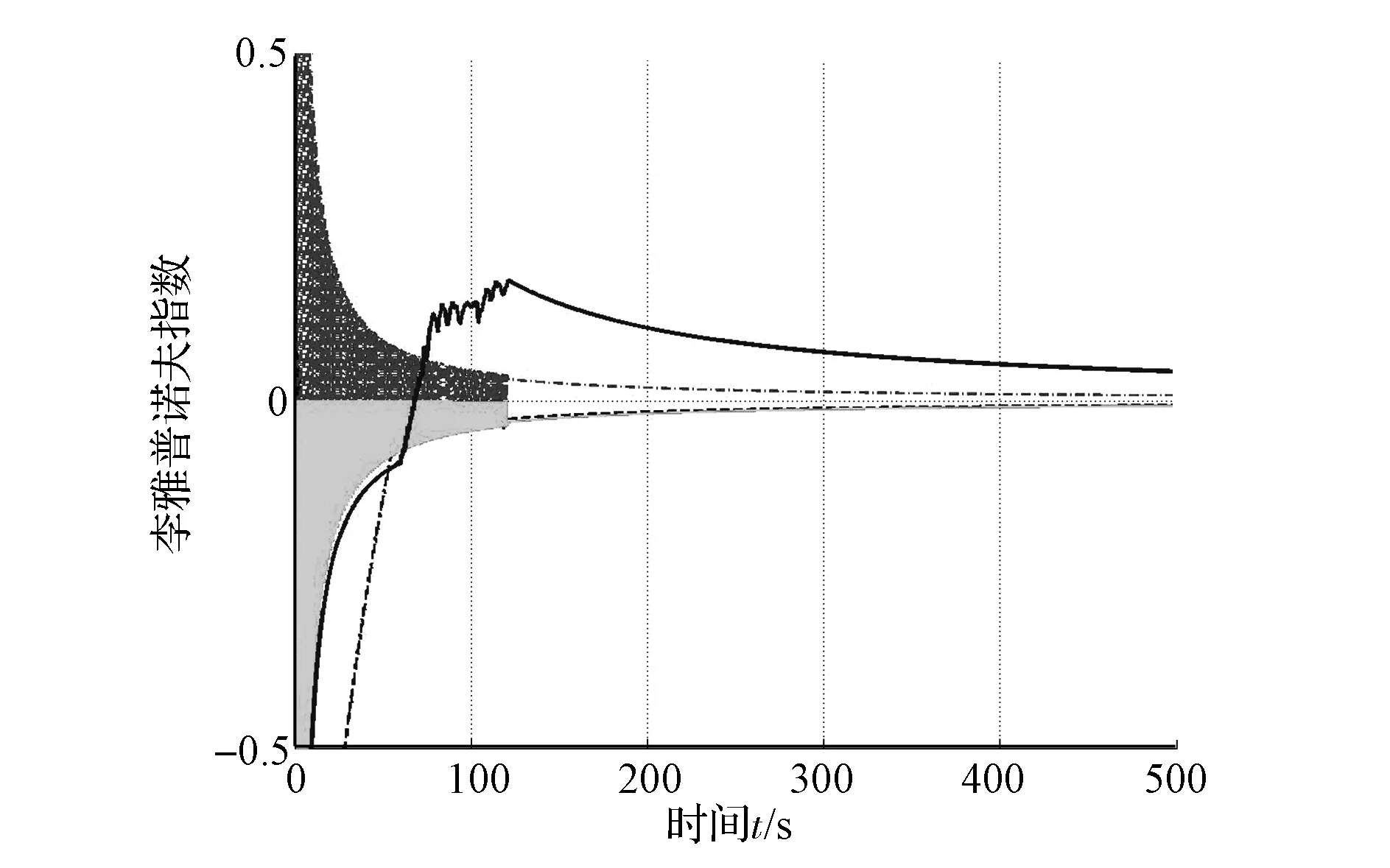
圖37 李雅普諾夫指數(T d＝100N·m)

目前，汽車主動安全控制系統通常以分層控制的結構進行設計[17]。這種結構的優點是能將復雜的輪胎力學特性與實際的受控對象，即汽車的運動狀態進行解耦，符合汽車動力學控制問題的本質，便于工程應用。但這種控制結構是通過協調各種子系統使汽車恢復穩定，而不是從汽車的運動狀態出發預防汽車的失穩。本文中的研究結果表明，如果從控制代價和可控效果的角度考慮，預防汽車失穩的控制方法其所需的控制能量低，控制效果好。

4 結論

(1)分析了不同驅動模式下，驅動力矩對系統分岔特征的影響。結果表明：與前輪轉角相似，驅動力矩的大小將直接影響汽車動力學系統的分岔特征。因此，在分析汽車的動力學分岔特征時應同時考慮前輪轉角和驅動力矩兩個分岔參數的影響。

(2)以前輪驅動模式為例，分析了5自由度汽車動力學系統在周期前輪轉角輸入條件下，系統分岔特征的動力學演變過程。結果表明：汽車動力學特征將由穩定的準周期運動過渡到混沌運動。

[1] ROSSA F D，GOBBIM，MASTINU G，et al.Bifurcation analysis of a car and drivermodel[J].Vehicle System Dynamics，2014，52(S1)：142-156.

[2] FARRONI F，RUSSO M，RUSSO R，et al.A combined use of phase plane and handling diagram method to study the influence of tyre and vehicle characteristics on stability[J].Vehicle System Dynamics，2013，51(8)：1265-1285.

[3] SADRIS，WU C.Stability analysis of a nonlinear vehiclemodel in planemotion using the conceptof Lyapunov exponents[J].Vehicle System Dynamics，2013，51(6)：906-924.

[4] 余志生.汽車理論[M].北京：機械工業出版社，2009.

[5] INAGAKIS， KUSHIRO L， YAMAMOTO M.Analysis on vehicle stability in critical cornering using phase-plane method[J].Jsae Review，1994，16(2).

[6] ONO E，HOSOE S，TUAN H D，et al.Bifurcation in vehicle dynamics and robust frontwheel steering control[J].IEEE Transactions on Control System Technology，1998，6(3)：412-420.

[7] ONO E，HOSOE S，TUAN H D，et al.Robust stabilization of vehicle dynamics by active frontwheel steering control[C].Proceeding of the 35th conference on Decision and Control， Kobe， Japan，December，1996.

[8] CATINO B， SANTINIS，BERNARDOM.MCSadaptive control of vehicle dynamics：An application of bifurcation techniques to control system design[C].Proceedings of the 42nd IEEE Conference on Decision and Control， Maui， Hmaii USA， December，2003.

[9] VINCENT N.Vehicle handling， stability， and bifurcation analysis for nonlinear vehiclemodels[D].USA，Washington D C：University of Maryland，2005.

[10] SHEN Shuiwen， WANG Jun，SHIPeng.Nonlinear dynamics and stability analysis of vehicle planemotions[J].Vehicle System Dy-namics，2007，45(1)：15-35.

[11] 劉麗，儲江偉，施樹明，等.車輛縱向加速度對操縱穩定性的影響分析[J].振動與沖擊，2009，28(6)：145-149.

[12] LIU L， SHI S， SHEN S， et al.Vehicle planar motion stability study for tyresworking in extremely nonlinear region[J].Chinese Journal of Mechanical Engineering，2010，23(2)：185-194.

[13] HORIUCHIS，OKADA K，NOHTOMIS.Analysis of accelerating and braking stability using constrained bifurcation and continuation methods[J].Vehicle System Dynamics，2008，46(S1)：585-597.

[14] WANG Xianbin， SHIShuming， LIU Li， etal.Analysis of driving mode effect on vehicle stability[J].International Journal of Automotive Technology，2013，14(3)：363-373.

[15] KIENCKE U，NIELSEN L.Automotive control systems[M].New York： Springer，2000.

[16] PACEJKA H B.Tyre and vehicle dynamic[M].Oxford：Elsevier，2006.

[17] 喻凡，李道飛.車輛動力學集成控制綜述[J].農業機械學報，2008，39(6)：1-7.

An Analysis on the Effects of Driving Torque on Vehicle Steering and Driving Bifurcation

W ang Xianbin1＆Shi Shum ing2
1.Traffic College， Northeast Forestry University， Harbin 150040； 2.Traffic College， Jilin University， Changchun 130025

To study the effects of driving torque on vehicle dynamics stability，on the basis of five degree of freedom(5 DOF)，two dimensional nonlinear dynamicsmodel of vehiclewith driving torque involved，and using the steering angle of frontwheel as an intermediate variable，a corresponding 7 DOF autonomous system model is established for analyzing the effects of driving torque on the dynamics features of vehicle steering and driving bifurcation under different drivingmodes.Taking a front-wheel-drive vehicle as an example，the dynamic evolution process of driving torque effects on steering and driving bifurcation is analyzed by using phase space，the time sequence of state variables，power spectral density and Lyapunov exponents.The results show that themagnitude of drive torque directly affects the bifurcation characteristics of vehicle dynamics system， and both bifurcation parameters， i.e.the steering angle of frontwheel and driving torque should be concurrently considered in analyzing the dynamic bifurcation characteristics of vehicle.

vehicle nonlinear dynam ics； driving torque； steering and driving coupling condition； bifurcation；chaos

10.19562/j.chinasae.qcgc.2017.10.013

?中央高校基本科研業務費專項資金(2572015CB15)、黑龍江省自然科學基金(E2015052)和國家自然科學基金(51475199)資助。

原稿收到日期為2016年8月9日，修改稿收到日期為2016年12月15日。

王憲彬，副教授，博士，E-mail：xbwang10＠ 163.com。