帶鴨翼的彈性高超聲速飛行器非線性控制
祝 姣,陳萬春,馬洪忠,楊志紅
(1. 北京航空航天大學 宇航學院,北京 100191;2. 中國航天科工集團公司三院無人機技術研究所,北京 100074;3. 北京空天技術研究所,北京 100074)
2016-06-12;
2017-07-05。
祝姣(1988—),女,博士,研究方向為高超聲速飛行器動力學建模與控制。E-mailzhujiao0406@126.com
帶鴨翼的彈性高超聲速飛行器非線性控制
祝 姣1,3,陳萬春1,馬洪忠2,楊志紅3
(1. 北京航空航天大學 宇航學院,北京 100191;
2. 中國航天科工集團公司三院無人機技術研究所,北京 100074;
3. 北京空天技術研究所,北京 100074)
高超聲速飛行器縱向靜不穩定、非最小相位和突出的彈性效應等特性給飛行器控制系統設計帶來嚴峻挑戰。針對該問題,文中采取鴨翼作為附加俯仰控制舵面與升降舵進行聯動控制的策略,以改善高超聲速飛行器的非最小相位特性和嚴重的彈性效應,從而達到提高控制性能的目的。首先,給出了考慮彈性模態的高超聲速飛行器動力學模型;其次,研究了鴨翼對飛行器非最小相位特性以及彈性模態響應的影響,并給出合適的鴨翼布局位置和鴨翼/升降舵聯動增益參數;最后,采用基于反饋線性化方法和LQR理論的非線性控制器對彈性飛行器進行控制,對比分析了鴨翼聯動控制對閉環控制性能的改善作用。研究結果表明,合理的鴨翼配置可以緩解系統的非最小相位特性帶來的不利影響,同時避免了控制輸入對特定彈性模態的激勵,從而達到提高彈性高超聲速飛行器控制性能的目的。
高超聲速飛行器;鴨翼;非最小相位;彈性模態;反饋線性化;非線性控制
0 引言
吸氣式高超聲速飛行器由于采取機體/發動機一體化設計,推力作用線在質心之下,前體升力和發動機推力會產生較大的抬頭力矩,造成飛行器的俯仰通道靜不穩定[1-2]。而采用安裝于機體尾部的大尺寸升降舵面進行俯仰通道控制時,必然會帶來嚴重的非最小相位問題。飛行器的靜不穩定特性和非最小相位特性分別構成了控制系統設計帶寬的下限和上限約束,嚴重限制了控制系統的設計空間和可達閉環性能[3]。高超聲速飛行器一般采取細長體構型和輕質結構設計,導致彈體結構頻率較低[4],而靜不穩定特性要求較高的控制頻帶,導致低階彈性模態頻率與控制系統帶寬交疊,以至于控制指令能夠激勵彈性振動,帶來嚴重的彈性穩定問題。
不考慮防熱等其他實際因素的影響,單純從控制角度來看,采取鴨翼作為冗余的俯仰控制舵面,不僅可以緩解飛行器的非最小相位特性,改善飛行器低速時的操縱性[5],還能給控制器設計提供更大的設計空間,提高飛行器的可達控制性能。文獻[2]研究了鴨翼對飛行器航跡動力學的影響,通過鴨翼與升降舵聯動控制來提高系統右半平面傳輸零點的頻率,使得系統不穩定零極點之間的頻率間隔加大,從而緩解甚至消除非最小相位特性對控制系統的限制。文獻[6]研究了采用鴨翼作為附加執行機構,以消除控制舵面對升力的氣動耦合項。由于彈性機體振動的主要激勵源來自于舵面產生的控制力,文獻[7]指出,通過采用多舵面聯合控制,可實現在滿足對剛體運動控制的同時避免激勵指定的低階彈性運動模態,從而實現提高飛行器飛行品質的目的。文獻[8]研究了彈性高超聲速飛行器的魯棒輸出反饋控制問題,鴨翼作為額外的控制舵面,結合角速率反饋,達到鎮定飛行器的不穩定零動態的目的。文獻[9]采用鴨翼聯動控制策略,用于消去模型的非最小相位特性,在此基礎上設計了基于反步法的魯棒自適應控制。
綜上所述,采用鴨翼作為附加的控制舵面,可極大程度地緩解飛行器控制系統設計所面臨的困難。本文借鑒了文獻[2,6]等提出的附加鴨翼聯動控制,采取合理的配置策略,來同時達到消除非最小相位特性和抑制彈性模態的目的,從而提高高超聲速飛行器非線性控制器性能。
1 彈性高超聲速飛行器模型
本文借鑒文獻[4]的動力學模型建模方法,該模型采用激波-膨脹波理論計算定常氣動力,采用當地活塞流理論計算彈性振動帶來的非定常氣動力。結構動力學建模時采用自由梁假設條件,因此飛行器剛體彈性之間不存在慣性耦合,剛彈耦合只體現在氣動力和廣義力中。彈性高超聲速飛行器縱向運動方程如下:
(1)

基于基礎理論所推導的模型中力和力矩的計算過于復雜,難以開展模型特性分析和控制器設計。因此,文獻[9]對初始模型中的氣動力和力矩進行了曲線擬合,得到力和力矩的簡化表達式如下:
(2)
其中,zT為推力偏心力臂,各氣動力系數和力矩系數如下式給出:
(3)
由式(2)、式(3)可知,鴨翼對飛行器的動力學特性影響主要表現在其對升力L、阻力D、俯仰力矩M以及彈性模態廣義力Ni的額外貢獻。
對式(1)進行配平并進行小擾動線性化,圖1為在h=25 908 m、V=2347.6 m/s時,原系統開環極點和傳輸零點圖,其中輸入u=[Φ,δe]T,輸出y=[V,γ]T。由圖1可知,系統存在一個不穩定極點s=2.47和不穩定傳輸零點s=4.08,該零點和極點之間頻率間隔很小。由于不穩定零點和極點分別構成了控制系統帶寬的上限和下限約束,因此控制帶寬的設計空間較小。
此外,由圖1可知,系統存在三階彈性模態,其中一階模態彈性振動頻率較低,由于靜不穩飛行器需要高帶寬控制器來保證穩定性,低階彈性頻率與控制帶寬頻率相近,控制指令容易激勵彈性模態,從而引起結構控制耦合問題。
為了改善系統非最小相位特性和抑制彈性振動,本文研究鴨翼作為冗余舵面,與升降舵進行聯動控制。本文假設升降舵大小和安裝位置均保持不變,鴨翼的尺寸固定,并與升降舵以增益kec進行聯動,其中kec≤0。
當鴨翼以增益kec與升降舵聯動控制時,相關的氣動系數等效為
(4)
2 鴨翼對非最小相位零點的影響
采用尾舵控制的飛行器,航跡響應均具有非最小相位特性,即傳遞函數γ/δe有一個不穩定零點。由文獻[10]可知,該傳遞函數的分子可表示為
其中, 1/Tγ3=-1/Tγ2為沿虛軸對稱的一正一負的實根,1/Tγ3位于右半平面。
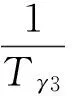
(5)
其中
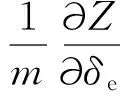
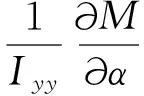
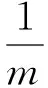
定義瞬時轉動中心為lcor=Zδe/Mδe,并代入式(5),有
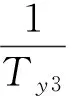
(6)
由此可見,可通過調整lcor來調整不穩定傳遞函數零點的位置。顯然,系數Zα<0,且對于不穩定飛行器來說,Mα>0。零點頻率變化趨勢如圖2所示,當lcor>0時,1/Tγ3為實數,且其頻率隨lcor減小而增加;當lcor=0,1/Tγ3頻率理論上將達到無窮;當Zα/Mα≤lcor<0時,1/Tγ3變成虛數,當lcor=Zα/Mα時,頻率為零;lcor 由于lcor由舵面產生的升力和俯仰力矩所決定,采用鴨翼與升降舵聯動控制,可通過調整聯動增益kec和鴨翼的位置xδe來調節lcor到需要位置,lcor表達式變為 (7) 為了便于分析,令k=-kec·(Zδc/Zδe),此時式(7)變為 (8) 易知式(8)的分母項恒為正。由圖2可知,當取k=1時,lcor=0,鴨翼產生的升力剛好抵消升降舵產生的升力,不穩定零點移向無窮遠處。當0≤k<1時,lcor>0,零點為不穩定實根,且隨著xδe朝向質心后移,鴨翼所產生的力矩變小,從而lcor逐漸變大。當k>1時,lcor<0。如上分析可知,當k=1時,零點的頻率可達到最大,從而留給控制系統帶寬設計空間最大。 高超聲速飛行器細長體外形、輕結構設計導致機體彈性模態頻率較低,與控制系統帶寬交疊,導致控制指令能夠有效激勵彈性模態,從而引起彈性失穩。采用鴨翼作為附加的控制舵面,與升降舵進行聯動控制,合理選擇鴨翼位置和控制增益,則可滿足對剛體運動控制的同時避免激勵一階彈性模態。此時,控制舵面產生的廣義力為 (9) 代入式(9),得到如下關系式: φ1(xδc) (10) φ1(xδe)-kφ1(xδc)] (11) 由式(11)可知,可通過調整增益k及鴨翼位置xδc來降低舵面指令對一階彈性模態的激勵。 前兩節研究了鴨翼對高超飛行器開環系統的影響,下面將結合反饋線性化和LQR理論,針對彈性高超聲速飛行器設計魯棒非線性控制器,在此基礎上,研究鴨翼聯動控制對飛行器閉環性能的影響,并進行仿真驗證。 為了采用反饋線性化方法,將彈性動力學考慮成一種未建模擾動,即不對其直接進行控制,只是通過選擇合適的鴨翼配置來避免舵面指令對彈性模態的激勵作用。 為了滿足相對階要求,忽略掉控制舵面所產生的升力和阻力項。此外,將發動機系統視為如下二階動態系統,指令Φc作為新的輸入變量: (12) 根據經典的輸入輸出線性化方法,通過對輸出變量求導可以得到: (13) 其中 取控制指令如下式: u=G*-1(v-f*(x)) (14) 將式(14)代入式(13),得到: (15) 至此系統被線性化為2個解耦的偽線性子系統。針對上述偽線性系統,可采用帶積分補償的LQR方法來設計。經過反復嘗試,LQR的權值矩陣分別選擇為 QV=ding(10,1,1,1),RV=1 Qh=ding(1,10,1,1,1),Rh=0.05 通過經典的LQR求解過程,求解Riccatti方程得到控制矩陣KV、Kh。 定義坐標變換: 其中 偽控指令可寫成如下形式: 為了驗證本文設計的基于反饋線性化的LQR控制器和鴨翼配置方案的控制效果,對彈性高超聲速飛行器的非線性模型進行仿真。在h=25 908m,V=2 347.6m/s狀態點處,跟蹤100 m/s速度階躍指令和1000 m的高度階躍指令,指令均通過如下二階參考模型進行濾波: (16) 其中,ω=0.039,ζ=0.9,圖4給出了參考指令圖。 根據第2、3節的分析結果,為了使鴨翼消除非最小相位特性和抑制一階彈性模態,鴨翼的安裝位置選擇為滿足條件φ1(xδc)=φ1(xδe),聯動增益選為k=1。系統采用鴨翼聯動控制前后兩種情況的非線性仿真對比結果如圖5所示。從仿真結果可看出,所設計的控制器能夠快速平穩的跟蹤速度和高度指令,跟蹤誤差快速收斂,驗證了所設計控制器的正確性和有效性。 可看出,與無鴨翼情況對比,增加合理配置的鴨翼作為額外控制舵面時,消除了系統非最小相位特性,從而減小了控制器設計所用模型與系統真實模型之間的誤差,使得系統跟蹤誤差更小,且收斂速度更快;且經過合理配置,升降舵面與鴨翼對一階彈性模態的激勵力相互抵消,從而避免了控制系統對一階彈性模態的激勵,使得彈性模態響應被大幅削弱,閉環系統高頻震蕩被有效抑制,系統的穩定性得到增強。 圖6給出了控制指令的時間歷程。可見,鴨翼與升降舵進行聯動時,有效舵效增加,升降所需升降舵偏的指令更小,從而一定程度上可避免舵面飽和的出現,且舵面指令的震蕩幅值和震蕩時間也得到優化。 然而,除了實際工程中鴨翼所需面臨的嚴峻的氣動熱問題之外,單純從控制角度來看,鴨翼也會帶來一些消極的影響。從圖5可以看出,當采用鴨翼控制時,系統所需配平攻角變大,且增大的幅值較高。經分析,這是由于鴨翼抵消了升降舵產生的升力,使得飛行器整體升力變小,因此需要更大的攻角來達到新的升重平衡。由于高超聲速飛行器的需要較大的控制舵面來克服靜不穩定特性以及平衡發動機推力產生的抬頭力矩,使得舵面產生的升力對總升力貢獻很大,因此需要較大的攻角增量來補償被抵消的這部分升力。進一步分析,由于較大的攻角會產生更大的阻力,因此將需要更大的油門指令來平衡阻力,正如圖6所驗證。此外,從圖5中還可以看出,由于攻角產生的彈性模態廣義力也會變大,從而使得飛行器彈性模態的靜變形更加顯著。這些問題都會給飛行器帶來不利的影響,因此實際應用中需要折中考慮各方面的因素。 (1)鴨翼可有效改變不穩定傳輸零點的頻率,從而緩解甚至消除系統嚴重的非最小相位特性。 (2)調整鴨翼的增益和位置可減弱甚至消除控制指令對一階彈性模態的激勵,從而保證彈性模態的穩定性。 (3)仿真結果表明,經選擇合適的聯動增益和鴨翼位置,附加鴨翼控制可顯著提高閉環系統的穩定性和響應性能。 [1] Bolender M A,Doman D B. A nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J] Journal of Spacecraft and Rockets,2007,44(2):374-387. [2] Bolender M A,Doman D B. Flight path angle dynamics of air-breathing hypersonic vehicles[R]. AIAA 2006-6692. [3] 葛東明.臨近空間高超聲速飛行器魯棒變增益控制[D]. 哈爾濱:哈爾濱工業大學,2011. [4] Oppenheimer M W,Doman,D B,Bolendern M A,et al. A flexible hypersonic vehicle model developed with piston theory[C] //AIAA Atmospheric Flight Mechanics Conference and Exhibit,Hilton Head.South Carolina,2007. [5] Oppenheimer M W,Skujins T,Doman D B,et al. Canard-Elevon interactions on a hypersonic vehicle[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit.2008,Honolulu,Hwaii. [6] Parker J T,Serrani A,Yurkovich S,et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J] . Journal of Guidance,Control,and Dynamics,2007,30(3): 856-869. [7] David L R,Jackson E B,Buttrill C S. Simulation study of impact of aeroelastic characteristics on flying qualities of a high speed civil transport[R]. NASA/TP-2002-211943. [8] Sigthorsson D O,Jankovsky P,Serrani A,et al. Robust linear output feedback control of an airbreathing hypersonic Vehicle [J] . Journal of Guidance,Control,and Dynamics,2008,31(4) :1052-1066. [9] Fiorentini L. Nonlinear adaptive controller design for airbreathing hypersonic vehicle[D]. Ohio State University,2010. [10] McRuer D T,Ashkenas I,Graham D.Aircraft dynamics and automatic control,Chap.5[M].Princeton University Press,Princeton,NJ,1973:336-337. Nonlinearcontrolofflexiblehypersonicvehicleswithcanard ZHU Jiao1,3,CHEN Wan-chun1,MA Hong-zhong2,YANG Zhi-hong3 (1.School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China;2. UAV Technology Institute,Beijing 100074,China;3. Beijing Aerospace Technology Institute,Beijing 100074,China) For a hypersonic vehicle with unstable longitudinal dynamics, non-minimum phase and severe aeroelastic effects, the design of flight control system is a challenging task. The feasibility of the strategy using canard in conjunction with the elevator as an additional factor is investigated, aiming to eliminating the non-minimum phase behavior and suppress the elastic mode, and to improve the performance of control system. First, a flight dynamic model with flexibility effects is presented. Second, the effects of the placement and relative ganging gain of the canard on the non-minimum phase behavior and elastic modes are demonstrated. At last, with the design of a nonlinear controller based on feedback linearization and LQR technology, the performances of the strategies with and without canards are comparatively evaluated. The simulated results show that, with the placement and relative ganging gain carefully chosen, the proposed control strategy provides an increased level of closed loop performance by suppressing the non-minimum phase behavior and eliminating control excitation of the first elastic mode. hypersonic vehicles; canard; non-minimum phase; elastic modes; feedback linearization; nonlinear control V448 A 1006-2793(2017)05-0660-06 10.7673/j.issn.1006-2793.2017.05.022 (編輯:呂耀輝)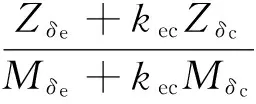
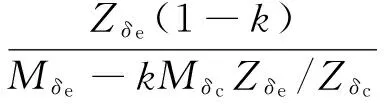
3 鴨翼對彈性模態運動的影響
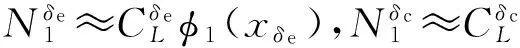
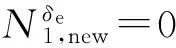
4 帶鴨翼的彈性高超聲速飛行器非線性控制器設計
4.1 基于反饋線性化的非線性控制器設計
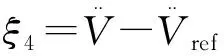
4.2 仿真結果分析
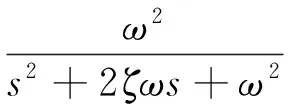
5 結論

