基于數字圖像相關法的復合材料結構失效分析

王 朝，常新龍，張有宏，張 磊，陳向東

(火箭軍工程大學 動力工程系，西安 710025)

2017-04-17；

2017-06-01。

國家自然科學基金(11302249)。

王朝(1992—)，男，碩士生，研究方向為失效物理與可靠性 。E-mail：2698963107@qq.com

基于數字圖像相關法的復合材料結構失效分析

王 朝，常新龍，張有宏，張 磊，陳向東

(火箭軍工程大學 動力工程系，西安 710025)

針對纖維增強復合材料失效機理復雜的問題，采用數字圖像相關法對拉伸試驗中的復合材料表面位移進行數字化處理，建立了基于Hashin改進準則的結構模型，對比試驗和仿真結果，分析試件的失效過程和機理。運用蒙特卡洛方法和有限元法，討論并分析影響結果精度的因素。結果表明，數字圖像相關法能夠用于觀察和分析復合材料結構的失效過程；基于Hashin改進準則的仿真模型與試驗結果一致，可以作為進一步細觀力學分析的基礎；相對于其他結構參數，縱向拉伸強度對結果精度的影響更大。該結果可為復合材料可靠性分析提供理論參考。

數字圖像相關法；復合材料；結構模型；可靠性分析；失效

0 引言

復合材料以抗腐蝕性能好、耐熱性能優異、比剛度和比強度較高等優點，廣泛用于航空、航天領域[1-2]。同時，也因復合材料性能對于制作工藝的依賴性，材料與結構的同一性等特點，導致復合材料失效過程較為復雜，對復合材料的結構設計和可靠性評估造成較大影響。因此，研究纖維增強復合材料的失效過程和失效機理顯得尤為重要。

目前，對復合材料結構失效過程的研究，大多采用仿真計算和試驗驗證相結合的方式[3-5]。景釗等[4]建立壽命預測模型，對復合材料疲勞壽命進行預測，但所采用的樣本過少，模型精度有待驗證；樊鈺等[5]對纖維材料和基體材料的變化規律進行了分析，但是未涉及具體結構的變化。現有的研究對于層合板的具體失效機理涉及較少，尤其是試驗過程中的結構變化情況也需要作深入研究，而數字圖像相關法(Digital image correlation，簡稱DIC)作為一種新型的測量方法，能夠對結構表面全場位移和應變進行分析，可通過研究試件的應變場變化來分析失效過程。

針對炭纖維復合材料結構的失效過程和失效機理研究，本文采用數字圖像相關法(DIC)對復合材料結構進行數字化處理，觀測和記錄試件拉伸試驗過程中的應變云圖；分析失效機理，建立基于Hashin改進準則的拉伸試驗模型，對照試驗結果分析試件的失效過程；基于所建立的模型，運用蒙特卡洛抽樣方法研究影響結果精度的因素，為下一步將該方法應用于復合材料結構設計和可靠性分析等更廣泛的領域提供參考依據。

1 基本原理

1.1 復合材料基本力學方程

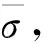
細觀應力-應變關系：

σ=C×ε

(1)

式中C為材料剛度矩陣。

宏細觀參數的關系：

已有大量工作研究了該方程的求解[6-8]，本文不再對過程進行贅述，只將結果介紹如下：

(2)

式中σ0為宏觀應力；R為纖維半徑；θ為圓心角；C(β,γ)為宏細觀剛度矩陣；Am(β,γ)為與細觀幾何結構以及子單元材料剛度相關的子矩陣；ε(β,γ)為細觀應變矩陣。

1.2 Hashin改進準則

在纖維增強復合材料拉伸試驗的過程中，復合材料試件會產生基體破壞、分層和纖維斷裂等損傷，現有的仿真計算大多是以Tsai-Hill準則、Tsai-Wu準則等為基礎開展的，無法詳細分析上述損傷過程，而Hashin準則可以準確表示這些損傷過程。但目前采用的Hashin準則在進行損傷變量計算時，所采用的唯象法無法表征和計算材料分散性，使得整個計算過程的損傷變化不連續。

考慮將參數的威布爾分布引入材料的損傷過程中，損傷過程可以由退化系數表示，由文獻[9]可知，在考慮威布爾分布后，其表達式為

(3)

式中m為威布爾分布的形狀參數；e為自然對數的底數；ε為拉伸過程中結構的應變；εf為材料的失效應變；Γ為伽馬函數。

改進后的Hashin準則如表1所示。

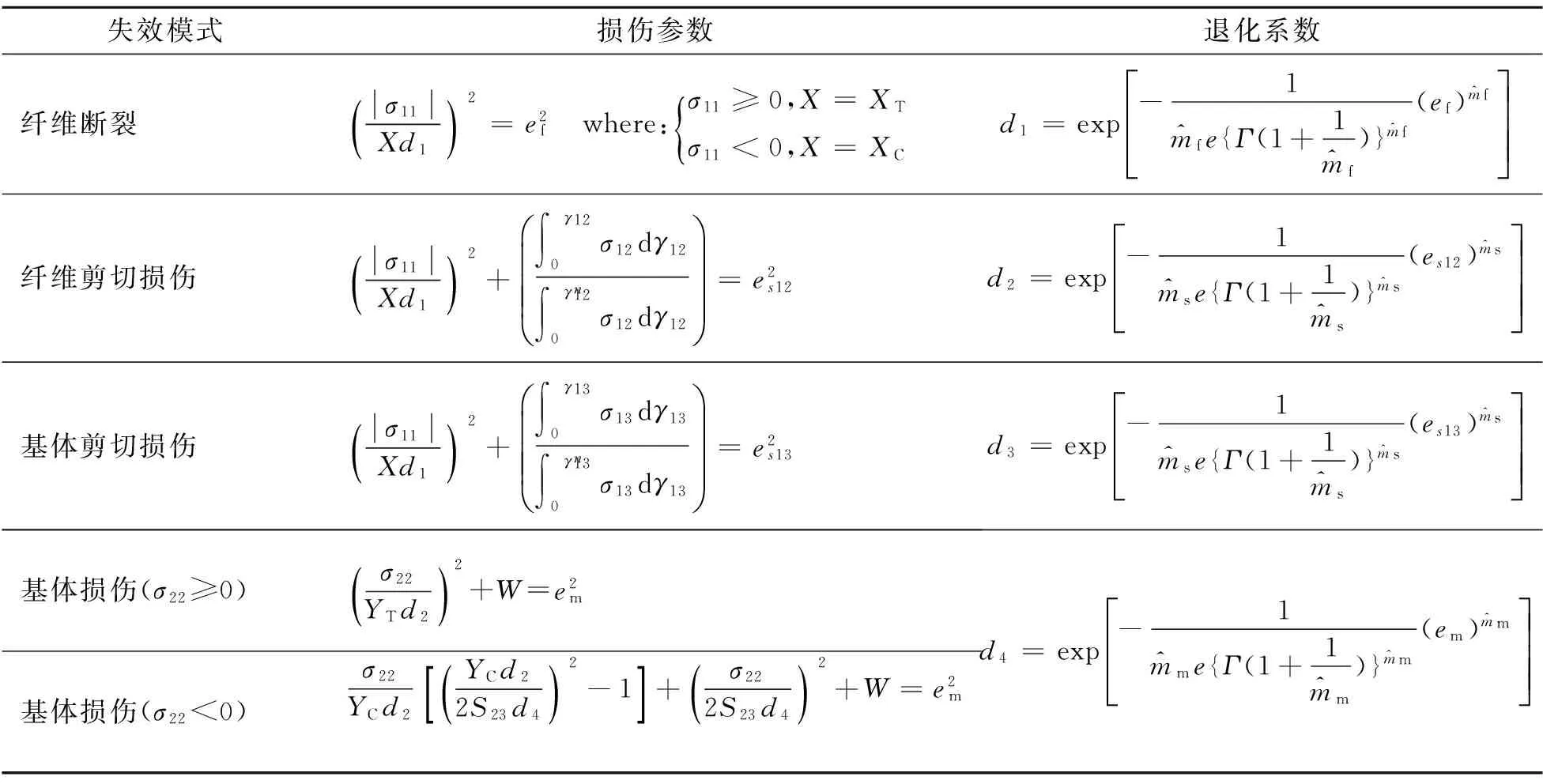
失效模式損傷參數退化系數纖維斷裂σ11Xd1()2=e2f where:σ11≥0,X=XTσ11<0,X=XC{d1=exp-1^mfe{Γ(1+1^mf)}^mf(ef)^mfé?êêêù?úúú纖維剪切損傷σ11Xd1()2+∫0γ12σ12dγ12∫0γn12σ12dγ12?è?????÷÷÷=e2s12d2=exp-1^mse{Γ(1+1^ms)}^ms(es12)^msé?êêêù?úúú基體剪切損傷σ11Xd1()2+∫0γ13σ13dγ13∫0γn13σ13dγ13?è?????÷÷÷=e2s13d3=exp-1^mse{Γ(1+1^ms)}^ms(es13)^msé?êêêù?úúú基體損傷(σ22≥0)σ22YTd2()2+W=e2m基體損傷(σ22<0)σ22YCd2YCd22S23d4()2-1[]+σ222S23d4()2+W=e2md4=exp-1^mme{Γ(1+1^mm)}^mm(em)^mmé?êêêù?úúú

在以上各式中W計算公式為

(4)

由文獻[10]可知，在對失效模式進行計算時，必須考慮耦合作用影響。出于簡化模型的考慮，本文認為損傷是不可逆過程。因此，在實際計算過程中，第n+1步的退化系數應取n和n+1步之間的最小值，即

1.3 數字圖像相關法

數字圖像相關法(Digital Image Correlation，簡稱DIC)，又稱數字散斑相關法(Digital Speckle Correlation Method，簡稱DSCM)，主要應用于計算機視覺技術領域。

數字圖像相關測量技術是圖像處理、技術識別和計算機技術結合的產物，通過將物體表面隨機分布的斑點作為變形載體，利用相關算法進行圖像處理后得到變形信息，研究和分析結構表面在外載荷或其他因素作用下的全場位移和應變。DIC測量系統一般由CCD攝像機、圖像采集卡和計算機組成，該系統測量范圍廣且自動化程度高。

2 復合材料結構試件拉伸試驗

2.1 試驗設計

試驗參考GB/T 3354—2014《定向纖維增強聚合物復合材料拉伸性能試驗方法》，采用環氧樹脂和T700炭纖維制備試驗所用復合材料的試件，由參考文獻[10]可知，該材料屬性如表2所示，試件尺寸為250 mm×25 mm×2 mm，按照[±62/02/62/0]s的順序進行鋪設。試驗時采用環氧樹脂鋁制加強片，來保證試件端部不受損傷。

采用微機控制電子萬能試驗機上進行準靜態拉伸試驗，運用攝像機檢測試件表面位移變化。測試系統所用的傳感器是CMOS攝像機，應用ARAMIS進行圖像后處理，得到應變場和位移場。

2.2 試驗結果分析

應用DIC得到試件表面應變場，選取其中一次試驗結果進行分析。圖1顯示了拉伸試驗中試件表面應變變化情況。

復合強度參數取值尺度形狀復合模量參數取值內聚性能參數取值XT/MPa248021.8E1/GPa123.4t1/MPa32.4XC/MPa951.414.6E2/GPa9.27t2/MPa68.8YT/MPa32.422.6ν120.31t3/MPa68.6YC/MPa137.710.5G12/GPa3.8GⅠC/(N/m)425S12、S13/MPa77.520.0G13/GPa3.8GⅡC/(N/m)1030S23/MPa68.640.0G23/GPa3.2GⅢC/(N/m)1030

由圖1(a)可知，試驗開始時，試件表面應變率較為均勻，在0.1%左右；在平均應變率達到0.54%時，試件表面62°鋪層沿纖維方向產生明顯應變率變化，最大應變率接近0.9%，此時發生初次破壞，如圖1(b)所示。拉伸試驗過程中，試件兩端位移最大，由于第一層與第二層鋪層角度相反，相對的位移導致兩端的層間剪切力最大，在拉伸載荷共同作用下，試件兩端位置最先沿著拉伸方向發生基體破壞和輕微纖維斷裂破壞。在試件平均應變率達到1.68%時，試件中部的應變率發生明顯突變，達到2.2%，此處產生二次破壞。由圖1(c)可知，此時試件受力結構主要是0°方向鋪層，因此主要失效模式是纖維斷裂。±62°鋪層在層間作用力下，隨著0°鋪層形變而發生進一步破壞，二次破壞發生位置在試件中間位置。此后，主要由±62°鋪層未斷裂的纖維承受外部載荷，但是纖維方向與外部載荷方向并不一致，很快就因斷裂而發生結構破壞。應變率達到1.82%時，試件結構破壞較為嚴重，由圖1(d)可看出，纖維完全發生斷裂，試件徹底失效。

試件受到破壞時的失效應力統計結果如圖2所示。由圖2可知，該批樣品失效應力分布較為分散，主要位于[1050 MPa，1160 MPa]區間內，平均值是1110 MPa，失效應變分布與應力分布較為一致，主要位于區間[1.72%，1.83%]，平均值是1.78%。由結果可知，應力和應變相關性較好。

3 拉伸試驗仿真分析

由于DIC只能處理試件表面應變場，無法將內部結構變化進行數字化處理，所以為了更加細致地分析結構的失效機理，同時與DIC結果形成對比，運用Abaqus軟件對拉伸試驗進行仿真計算。

3.1 有限元模型的建立

在仿真建模時做如下假設：在結構試件成型前后，纖維和基體的結構形式和力學性能等均不發生明顯變化，各層面之間粘接良好，且沒有缺陷；在試件受到拉伸載荷作用時僅產生線彈性變化，試件中的殘余應力和試驗過程中的干擾因素對試驗影響忽略不計。

纖維增強復合材料結構試件依據表2賦予材料屬性，有限元模型共分12個鋪層，采取對稱鋪層的方式排布，采用Abaqus仿真軟件中的cohesive單元模擬試驗時試件出現的分層損傷。

3.2 仿真結果分析與研究

對上述有限元模型進行計算，得出復合材料結構試件的參數變化過程。由于DIC主要是處理得到應變云圖，為便于對比分析，所有參數均以應變率為自變量。對所得結果進行數據處理后，得出應力-應變曲線、纖維失效和基體失效隨應變變化曲線等。

(1)應力-應變曲線分析

對應力-應變曲線進行分析和處理后，其平均曲線如圖3實線所示。

由圖3可知，層合板結構應力-應變仿真曲線與真實應力-應變曲線相比一致性較好，特別是在應變率小于0.55%時，仿真曲線和試驗結果完全重合，應力-應變呈線性關系，此時層合板并未發生明顯結構破壞。當應變率為0.55%時，兩條曲線斜率均有明顯下降，這是由于此處層合板發生拉伸破壞，仿真模型的剛度矩陣和材料細觀結構均發生退化。當應變率大于0.55%后，曲線基本走勢一致但是未能完全吻合，仿真曲線斜率大于試驗曲線。

分析可知，本文所用的剛度退化矩陣是自行設定，與試驗過程中材料損傷情況有一定出入，導致曲線結果不完全一致；當應變率大于1.71%時，試件結構損傷嚴重但仍未完全失效，試驗曲線斜率變小，直至應變率大于1.78%時，曲線才呈現明顯下降趨勢，而在進行仿真計算時，所設定的剛度矩陣在應變率達到1.73%時已完全退化，無法繼續計算，曲線呈現下降趨勢。雖然試驗應變率大于仿真應變，但拉伸試驗過程中試件的損傷更復雜，參數退化更嚴重，因此由仿真計算得到的失效應力1198 MPa大于試驗得到的失效應力平均值1103 MPa。

(2)纖維失效與基體失效隨應變率變化曲線分析

由于在進行仿真計算時，采用的是對稱鋪層的方式建立模型，因此對稱鋪層的纖維失效和基體失效情況完全相同，結果圖4所示。Hashin準則的退化系數并不完全表示結構失效情況，但在一定程度上可反應各成分的損傷情況，基于此本文對拉伸試驗中各結構變化過程分析如下。

對比圖4可知，在試驗開始時，0°鋪層的破壞方式是纖維斷裂， ±62°鋪層的破壞方式以基體破壞為主，同時伴有纖維斷裂。應變率為0.58%時，±62°鋪層的基體開始開裂而后迅速破壞，整體結構產生初次破壞，此后整體結構的拉伸載荷全部由0°鋪層承擔，其纖維破壞參數增長速率明顯加快；應變率達到1.77%時，0°鋪層纖維開始破壞而后迅速斷裂，結構產生二次破壞，載荷再次由±62°鋪層的剩余纖維承受，此后破壞極為迅速；應變率達到1.81%時，結構試件完全失效。整個失效過程與DIC所記錄的層合板失效過程較為一致。

由以上分析可知，所建立的模型與試驗過程一致性較好，能較為準確地對纖維增強復合材料的失效過程進行分析。

4 精度影響因素分析

在應用DIC進行分析時，精度對于結果分析時的有效性和準確性影響很大，所以有必要研究精度的影響因素。由于DIC是以位移和應變為處理對象，位移和應變越大，結果分析的精度越高。由拉伸試驗結果可知，應變與應力相關性較高。因此，本文認為對應力影響越大的因素對結果精度影響也就越大。

由前文結果分析可知，可運用所建立的模型分析細觀參數對宏觀性能的影響。本文主要對復合材料試件的失效過程進行研究，因此主要討論試件的失效應力。在拉伸試驗中壓縮參數對試件結構失效的影響較小，所以在分析參數對性能的影響時，主要討論縱向拉伸強度XT(纖維方向)、橫向拉伸強度YT(垂直于纖維方向)、彈性模量E1和E2以及泊松比ν12。

按照表2所示參數分布，運用蒙特卡洛方法對縱向拉伸強度XT進行采樣，運用有限元方法計算失效應力，對結果進行分布擬合，可得如圖5所示結果。

由圖5可知，采用正態分布和威布爾分布均對統計結果進行描述效果均較為理想。正態分布擬合之后平均值是1188 MPa，方差是36，威布爾分布參數分別是1208 MPa和29 MPa，兩種分布擬合與試驗結果的平均值1110 MPa較為接近。同理，對橫向拉伸強度YT，彈性模量E1、E2和泊松比ν12進行采樣后，計算失效應力并擬合其分布，結果如圖6～圖8所示。

由圖6可知，對于橫向拉伸強度YT，正態分布平均數是1190 MPa，方差是1，威布爾分布參數分別是1191、1194 MPa，正態分布擬合效果更好。由圖7、圖8可知，當彈性模量E1、E2和泊松比ν12發生變化時，失效應力變化范圍極小，因此不再對其結果分布進行擬合。

綜上所述，縱向拉伸強度產生變化時，失效應力分布在[1220 MPa, 1300 MPa]之間，分布較為廣泛，當橫向拉伸強度產生變化時，失效應力主要在[1188 MPa, 1192 MPa]之間變化，要明顯小于縱向拉伸強度的響應范圍，說明所有細觀參數中縱向拉伸強度對復合材料結構的失效應力影響最大。由以上分析可知，運用本文所制備的試件進行拉伸試驗時，縱向拉伸強度XT對結果的精度影響最大。

5 結論

(1)對試件進行拉伸試驗，由統計結果可知，該批試件的失效應力分布較為分散，平均值是1110 MPa，失效應變分布與應力分布較為一致，平均值是1.78%。

(2)采用建模仿真結合實驗結果，分析了復合材料層合板試件的拉伸失效過程：首先以基體失效為主，而后發生纖維失效，當最大應變大于1.81%時，試件完全失效，所得結論與試驗結果較為一致，證明了所建立模型的適用性與準確性。

(3)運用所建立的模型分析影響結果精度的因素，由結果可得，在本文所采用的試件進行拉伸試驗時，結構參數對結果精度均會造成影響，其中縱向拉伸強度XT對精度影響最大。

[1] Jeong H K,Shenoi R A. Probabilistic strength analysis of rectangular FRP plates using Monte Carlo simulation[J].Comput. Struct.,2000,76(3):219-235.

[2] 杜善義.先進復合材料與航空航天[J].復合材料學報，2007,24(1):1-12.

[3] Sriramula S,Chryssanthopoulos M K.Quantification of uncertainty modeling in stochastic analysis of FRP composite structures[J].Composites Part A:Appl.Sci.Manuf.,2009,40:1673-1684.

[4] 景釗，孫秦.復合材料多向層壓板疲勞壽命預測[J].固體火箭技術,2013,36(2): 237-242.

[5] 樊鈺，葉定友，陳汝訓.溫度影響下炭纖維/環氧樹脂復合材料性能預示[J].固體火箭技術,2013,36(6):831-835.

[6] 胡麗娟，張少睿，李大永，等.細觀參數對纖維增強金屬基復合材料宏細觀力學性能的影響[J].上海交通大學學報,2008,42(3):475-479.

[7] Aghdam M M，Dezhsexan A. Micromechanics based analysis of randomly distributed fiber reinforced composites using simplified unit cell model [J].Composite Structures,2005,71:327-332.

[8] Drago A，Pindera M J. Micro-macromechanical analysis of heterogeneous materials: Macroscopically homogeneous vs periodic;microstructures[J].Composites Science and Technology,2007,67(6):1243-1263

[9] 劉萬雷,常新龍,張曉軍,等．纏繞復合材料殼體低速沖擊損傷試驗與仿真研究[J].推進技術,2017,38(1):172-178.

[10] Eun-Ho Kim,In Lee. Low-velocity impact and residual burst-pressure analysis of cylindrical composite pressure vessels[J].AIAA Journal,2012,50(10):2180-2193.

Failureanalysisoffiberreinforcedcompositestructuresusingadigitalimagecorrelationmethod

WANG Chao,CHANG Xin-long,ZHANG You-hong,ZHANG Lei,CHEN Xiang-dong

(Department of Power Engineering,Rocket Force University of Engineering,Xi'an 710025,China)

Aiming at the complicated mechanism for the failure problem of fiber reinforced composite,a digital image correlation(DIC) method was used to obtain the evolution of strain field on specimen surface of the laminated sheet tensile test.A structural model was established as well based on improved Hashin criteria.The simulation results were compared with experimental ones to analyze the failure process and mechanism of the specimen.Based on Monte Carlo method and finite element method,the influence of Micro-parameters on the accuracy of the result was discussed and analyzed.The results indicate that the DIC is capable of analyzing and predicting the structural failure process.The established model based on improved Hashin criteria is in good agreement with the experimental results,which can be used as a basis for the further research on micromechanics.Compared with the other structural parameters,longitudinal tensile strength has a greater impact on the accuracy of the results.The results can provide theoretical reference for reliability of the composite materials.

digital image correlation;composite material;structural model;reliability analysis; failure

V258

A

1006-2793(2017)05-0614-06

10.7673/j.issn.1006-2793.2017.05.015

(編輯：呂耀輝)