例談高中數學解題中導數的易錯點
◆陳渙之
例談高中數學解題中導數的易錯點
◆陳渙之
高中數學知識不管是深度還是廣度,同初中數學知識點相比有了很大的提高,同時高中數學知識點之間的聯系較緊密,學生只有加強對相關知識點的理解才能為后續的學習打下良好的基礎。導數是高中數學學習當中的知識難點,所以本文對高中數學導數學習以及解題過程中容易出現的易錯點進行了具體的分析,以此提高學生的學習成績。
高中數學;導數解題;易錯點
一、未能對定義域引起高度的重視
在對最值進行求解的過程中,未能對函數變量的定義域引起高度的重視,導致了在解題的過程中出現了概念性的錯誤,為了能夠將措施的原因充分體現出來,下面進行相應的舉例說明。
有這樣一道例題:求出函數f(x)=ln(1+x)-x的單調性。
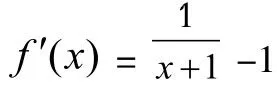
錯誤分析:根據已知條件以及定義進行分析可以得知原函數函數f(x)=ln(1+x)-x的定義域是,在解題的過程當中忽視了原函數的變量,所以也就忽視了定義域的變化。在這樣的情況之下,就造成解題思路以及解題的結果出現了錯誤。所以,原題正確的結果應該是“函數f(x)=ln(1+x)-x在(?1,0)上單調遞增”。
二、極大值和極小值的坐標點不明確
在進行函數極大值和極小值求解的時候,認為當原函數的導數等于0的時候,就是原函數的極值點。對導數相關知識點的理解不深刻不全面是存在這種錯誤思維的主要原因,認為當導數等于0的時候就可以求原函數的極值。
有這樣一道題:函數f(x)=x3-6x2+cx在x=t的時候有最小值g(t),求出g(t)的定義域以及值域。
錯誤的解法:首先對函數f(x)=x3-6x2+cx進行求導,就可以得出f′(x)=3x2?1212x+c,然后推導出:(x?2)2+c?1212,然后令f′(t)=0,那么就可以得出c=?3t2+12t。因為f(x)能夠在滿足條件的情況下取得極小值,所以f(x)=0有解,因此c<12,c=?3t2+12t<12,就可以得出t≠2,所以就可以求出g(t)的值域為:g(t)=f(t)=-2t3+6t2,其中 t≠ 2。
錯誤分析:在解答這道題的時候,我犯的錯誤是將f′(x)=0當做了f(t)的充要條件,在這道題當中,f′(x)=0應該是f(t)的必要條件。
正確的解法:c≥12的時候,f′(x)≥0,那么在這個時候f(x)沒有極值;c<12的時候,f′(x)=0兩個不同的實數根x1,x2,假如x1<x2,那么就可以得出x1<2<x2。進一步推導:當x<x1的時候,f′(x)>0,那么就可以得出f′(x)在(-∞,x1)內是增函數。當x1<x<x2的時候,f′(x)<0,f′(x)在(x1,x2)內是減函數。當x1>x2的時候,f′(x)>0,f′(x)在(x2,+∞)內是增函數。
所以就可以得出一下的結果:當f(x)在x1=x2的時候,導函數f′(x)在x1=x2的時候存在著極小值,而且只有一個。所以當t=x2且t>2的時候,就可以得出g(t)的定義域是(2,+∞),根據f(t)=3t2-12t+c=0,可以得出c=-3t2+12t,最終就可以推出 g(t)=f(t)=t3-6t2+ct=-2t3-6t2。
三、在導數學習以及計算的過程中未能有效理解導數的幾何意義
通過對導數相關知識點的學習可以得知,函數以及它的導數的幾何意義就是函數曲線在某一個點的切線的斜率,如果對這個知識點進行靈活運用,就能夠容易的解決相關的曲線切線方程。有這樣的一道題:曲線經過了點(1,1),求出該曲線的切線方程。
錯誤的解法:對y=-22x+x進行求導就可以得出:,然后將點(1,1)帶入到切線當中就可以得出原函數切線的斜率k=-3,所以就可以得出原函數的切線方程是y=-3x+4。

結束語
導數在高中數學的學習當中是十分重要的,雖然在學習的過程當中存在著一些問題,在解答有關導數題目的時候容易出現相應的錯誤。但是只要在學習的過程中加深對相關知識點的理解,加強導數題目的練習,掌握解題的思路以及技巧,就能夠有效減少解題的錯誤率,從而提高數學成績。
[1]羅沐奇.剖析高中數學導數問題易錯點[J].亞太教育,2016,33:70.
(作者單位:長沙市長郡梅溪湖中學)

