基于Laplace變換的RLC電路特性研究與仿真

劉德全， 周國清

(1. 天津大學 微電子學院， 天津 300072； 2.寧夏師范學院 物理與電子信息工程學院， 寧夏 固原 756000；3. 天津大學 遙感中心，天津 300072)

基于Laplace變換的RLC電路特性研究與仿真

劉德全1,2,3， 周國清1，3

(1. 天津大學 微電子學院， 天津 300072； 2.寧夏師范學院 物理與電子信息工程學院， 寧夏 固原 756000；3. 天津大學 遙感中心，天津 300072)

為了提高對電路中電阻、電感、電容的理解，對RLC串聯二階電路采用Laplace模型建立了傳遞函數，通過傳遞函數對電路的欠阻尼、臨界阻尼和過阻尼的工作狀態進行分析，對其狀態軌跡、頻率特性等進行了研究。在EDA軟件平臺中設計了RLC串聯電路，對3種工作狀態、狀態軌跡以及頻率特性曲線進行了仿真，得到了清晰的圖形。

拉普拉斯變換； RLC電路； 傳遞函數； 動態特性

RLC二階電路是最基本的電路之一，在RLC二階電路分析和建模仿真、RLC串聯諧振電路中的電感頻率特性、二階電路的衰減常數的估計、電路狀態軌跡、方波激勵下的二階電路的響應、RC濾波器優化等方面受到重視并進行了很多研究[1-11]。但是，相關研究多為時域分析，而在s域中分析得較少。本文通過Laplace變換將時域分析轉換為s域分析，方法簡單易懂，很容易得到電路的3種工作狀態、狀態軌跡圖和相關頻率特性曲線。

1 s域電路分析

1.1 s域電路建模

RLC串聯電路s域電路如圖1所示[12-19]。

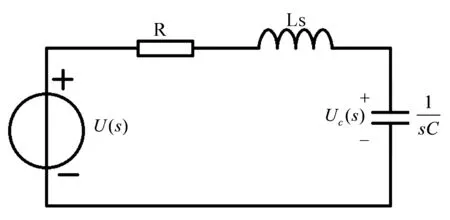
圖1 RLC串聯電路的s域電路圖

設電感、電壓的初始值為0，以電容電壓Uc為輸出變量，則電壓傳遞函數的Laplace變換方程為

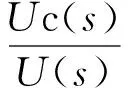
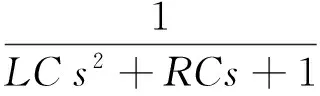
(1)

其中：

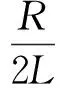
此時極點位于負實軸上，H(s)分母有(s-p1)和(s-p2)因子，它的自由響應函數包含2個不同的A1ep1tε(t)， (p1<0)和A2ep2tε(t)， (p2<0)的衰減指數函數，且極點離原點越遠，衰減得越快。自由響應與極點關系圖如圖2(c)所示。

圖2 極點與自由響應關系圖

1.2 狀態軌跡

1.3 頻率特性曲線

將s=jω代入(1)式，得到系統的頻率響應傳遞函數為

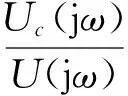
(2)

式中，|H(jω)|稱為幅頻響應，φ(ω)稱為相頻響應。當ω從0(或-∞)變動時，|H(jω)|和φ(ω)也隨之變換，繪制出其隨ω變化的曲線，就得到了幅頻特性曲線和相頻特性曲線。幅頻特性曲線和相頻特性曲線合稱為頻率特性曲線。如果在繪制曲線時，頻率以對數尺度表示，則得到的圖形分別稱為幅頻波特圖和相頻波特圖，總稱為波特圖。

2 電路特性參數仿真

2.1 動態電路的暫態和狀態軌跡

在EDA仿真軟件[22]中繪制如圖3所示電路。在圖中，Oscilloscope為四通道示波器，其中A通道為Uc信號，B通道為IL信號，C通道為CLOCK信號(1 Hz、1 V的方波電壓信號)。在進行狀態軌跡仿真時，x軸為Uc信號，y軸為IL信號，H1為電流控制的電壓源。由于該示波器只能采集電壓信號，因此，需將電感的電流信號轉換為電壓信號(線性轉換)。在該電路中，電流信號比較小，為了得到清晰的波形，其跨阻值設置較大，這里設置為500，即轉換關系為

U=500IL

(1) 當開關處于“1”位置時，即R=500 Ω，電路處于過阻尼狀態(仿真波形如圖4所示)，在所有的CLOCK、Uc和IL波形圖中，CLOCK信號為紅色，Uc信號為綠色，IL信號為藍色；

圖3 仿真測試電路

(2) 當開關處于“2”位置時，即R=200 Ω，電路處于臨界阻尼狀態，仿真波形如圖5所示；

(3) 當開關處于“3”位置時，即R=50 Ω，電路處于欠阻尼狀態，仿真波形如圖6所示；

(4) 當開關處于“4”位置時，即R=0 Ω，在理想電路時是等幅振蕩，要得到等幅振蕩波形，需要添加負阻抗元器件，在圖3中沒有負阻抗元器件，因此仿真波形應該是衰減的正弦波形，如圖7所示。

2.2 電路頻率特性曲線

按照圖8(a)所示電路設計仿真電路，采用頻率特性曲線圖表進行仿真，仿真結果如圖8(b)所示。其中，正弦波信號的頻率為100 Hz，幅度為1 V；黑色的波形線為幅頻特性曲線，紅色的波形為相頻特性曲線。很顯然，該電路具有低通濾波器的特征。

圖4 過阻尼狀態波形

圖5 臨界阻尼狀態波形

圖6 欠阻尼狀態波形

圖7 R=0時的波形

圖8 頻率特性曲線仿真

3 結語

在RLC二階串聯實驗電路中，用Laplace變換對RLC電路的暫態過程、狀態軌跡圖和頻率特性曲線進行分析，利用Proteus EDA軟件對電路的特性進行仿真，參數修改非常方便，并且降低了實驗成本、拓寬了實驗教學空間，有助于學生加深對基本元器件特性的理解，激發學習的積極性。

References)

[1] 孫文杰.Matlab電路仿真實驗常用建模方法[J].實驗室研究與探索,2016,35(7):80-84.

[2] 郝小江.RLC串聯電路暫態過程綜合實驗設計[J].實驗科學與技術,2016,14(1):39-41,94.

[3] 任兆香,顧海清,張倩，等.PSPICE仿真分析與二階動態電路教學法研究[J].實驗技術與管理，2016,33(6):117-125.

[4] 陳國杰,陳奎,周有平，等.電感頻率特性及在RLC串聯諧振電路中的應用[J].大學物理,2016,35(6):29-32.

[5] 劉松齡,熊新兵,陳首部，等.二階電路衰減常數的估計及誤差分析[J].中南民族大學學報(自然科學版),2015,34(2):100-103.

[6] 李瑞金.二階電路衰減系數的誤差分析[J].實驗科學與技術,2015,13(5):32-34.

[7] 李姿,李曼，王津.二階電路暫穩態過程與狀態軌跡的實驗研究[J].科技論壇，2013(8)：37-38.

[8] 陳杰,賀澤東,南楠.方波電動勢激勵下的RLC串聯電路共振特性研究[J].大學物理,2016,35(1):28-30.

[9] 劉曉文,薛雪,喬欣，等.方波激勵下的RLC串聯電路暫態響應仿真研究[J].實驗技術與管理,2015,32(1):112-115.

[10] 劉洪臣,陳東,劉雷.方波輸入下LC電路暫態過程實驗研究[J].實驗技術與管理,2014,31(2):23-25.

[11] 田聰.RC有源濾波器的優化設計[D].金華:浙江師范大學,2016.

[12] Hambley A R.電工學原理與應用[M].熊蘭,彭光金,孫韜，等譯.北京：電子工業出版社,2014.

[13] 吳大正.信號與線性系統分析[M].北京:高等教育出版社,2005.

[14] 邱關源,羅先覺.電路[M].北京:高等教育出版社,2008.

[15] Alexander C K, Sadiku M N O.電路基礎[M].段哲民,周巍,李宏，等譯.北京:機械工業出版社，2014.

[16] 秦曾煌.電工學[M].北京:高等教育出版社,2009.

[17] Nilsson J W, Riedel S A.電路[M].周玉坤,冼立勤，譯.北京:電子工業出版社,2015.

[18] 鄭君里,應啟珩,楊為理.信號與系統[M].北京:高等教育出版社,2011.

[19] 胡壽松.自動控制原理[M].北京:科學出版社，2013.

[20] 天煌科技實業有限公司.THKKL-2型控制理論實驗箱實驗指導書[EB/OL].(2010-12-03)[2017-04-10].https://wenku.baidu.com/view/14497b0bbb68a98271fefab3.html.

[21] 南京恒締科技有限公司.HD8662信號與系統實驗講義正文[EB/OL].[2017-04-10].http://www.docin.com/p-218347090.html.

[22] 劉德全.Proteus 8：電子線路設計與仿真[M].北京:清華大學出版社,2017.

Research and simulation of RLC circuit characteristics based on Laplace transform

Liu Dequan1,2,3， Zhou Guoqing1,3

(1. School of Microelectronics, Tianjin University, Tianjin 300072, China; 2. School of Physics and Electronic Information Engineering, Ningxia Normal College, Guyuan 756000, China；3. Remote Sensing Center, Tianjin University, Tianjin 300072, China)

In order to improve the understanding of RLC (resistance, inductance and capacitance) in the circuit, the transfer function is established by using the Laplace model for the RLC series two-order circuit. Through the transfer function, the working states of the underdamping, the critical damping and the overdamping of the circuit are analyzed, and their state trajectories and frequency characteristics, etc., are studied. The RLC series circuit is designed at the EDA software platform. The three working states, the state trajectories and the frequency characteristic curves are simulated, and the clear graphs are obtained.

Laplace transform; RLC circuit; transfer function; dynamic characteristics

TM133；TP391

A

1002-4956(2017)10-0108-04

10.16791/j.cnki.sjg.2017.10.027

2017-04-20修改日期2017-06-05

寧夏教育廳高等學校科學研究項目(NGY2016200)；寧夏高等學校本科教學質量與教學改革項目(2017(68));國家海洋局區域經濟創新示范項目(cxsf-039)

劉德全(1977—)，男，甘肅白銀，碩士，副教授，主要研究方向為電路仿真設計及信號處理.

E-mail：ldqzhh@163.com