復變函數解析的共軛復坐標解釋
滕遠江
(湖南工程學院,湖南 湘潭 411104)
復變函數解析的共軛復坐標解釋
滕遠江
(湖南工程學院,湖南 湘潭 411104)
解析函數是復變函數論的重要對象,為深刻揭示解析函數的本質特性,需要從不同角度刻畫函數的解析性。本文首先引入復變函數的共軛復坐標記號,探索復變函數在共軛復坐標下的微分特性,進而運用共軛復坐標解釋了復變函數的解析性。
復變函數;解析;共軛復坐標
1 復變函數的共軛復坐標記號
實數與復數之間存在著變換:
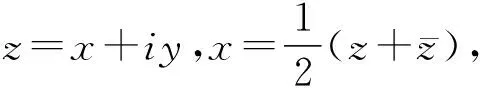
(1)
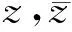
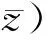
(2)
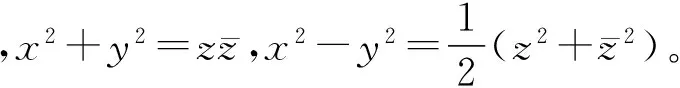

2 共軛復坐標下函數的微分
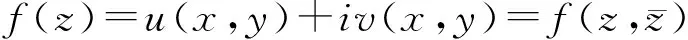
由(1)可得:
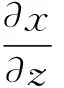
(3)
可以對復變函數f(z)進行形式偏導(二元泰勒公式可以具體解釋):
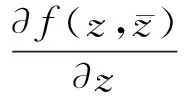
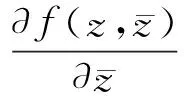
即:
(4)
另外,由(3)可得:
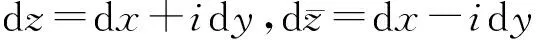
(5)
f的微分定義為du+idv,結合(5)有:
df=du+idv=(uxdx+uydy)+i(vxdx+vydy)
=(ux+ivx)dx+(uy+ivy)dy
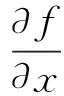
繼續演變,還有:
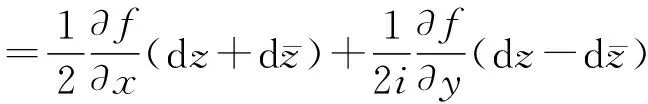
即f的全微分對:
(6)
(6)反映了f的全微分滿足一階微分形式不變性。
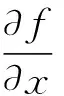
3 復變函數解析的共軛復坐標解釋
一般復變函數理論有:
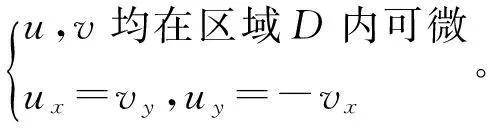
由(4)、(5)得:
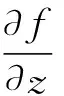
(7)
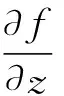
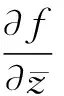
(8)
此時,由(6)知:
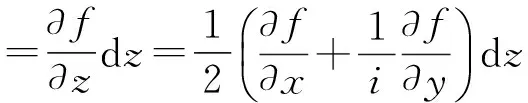
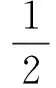
=(ux+ivx)dz
即得:
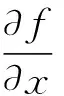
(9)
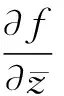
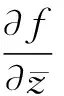
當一個解析函數f的導數f′在區域D上恒為零時,由(7)、(9)知f的實部u和虛部v關于實變量x,y的各個偏導數都恒等于零。因此u,v是常數,從而f在D上是常數。
由C.-R.方程知,區域D上解析函數f的實部u和虛部v只要有一個是常數,則f在區域D為常數[3]。
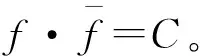
綜上所述:
解析函數f為常數?f′(z)≡0?u≡0或v≡0?|f|為常數
(10)
【定理※※】及(10)均為復變函數解析的共軛復坐標解釋[4]。
復變函數解析的共軛復坐標解釋運用到復積分理論中將產生巨大能量[5],將在今后的討論中展示。
[1] Ahlfors L.Complex Analysis. McGraw-Hill,1979.
[2] Jones G.A.Complex Functions-An Algebraic and Geometric Viewpoint[M].Singerman D.Cambridge Univerity Press,1987.
[3] 龔晟.簡明復分析[M].北京:北京大學出版社,1996.
[4] 楊澤恒,付卓如.大學復變函數課程與高中數學的銜接[J].大學數學,2013,29(01):15-17.
[5] 鐘玉泉.復變函數論(第4版)[M].北京:高等教育出版社,2013.
Conjugatecomplexcoordinateinterpretationofcomplexvariablefunction
TENG Yuan-jiang
(Hunan Institute of Engineering, Xiangtan 411104, China)
The analytic function is an important object of the complex function theory. In order to reveal the essential characteristics of the analytic function, it is necessary to describe the analytic function from different angles. In this paper, we first introduce the conjugate complex coordinate of the complex function, and explore the differential characteristic of the complex variable in conjugate complex coordinate, and then use the conjugate complex coordinate to explain the analytic property of the complex function.
Complex variable function; Analytic; Conjugate complex coordinate
O174.5
A
1674-8646(2017)18-0092-02
2017-06-16
湖南工程學院校級教改項目“本科公共數學教學的動力優化與模式革新”(2017)
滕遠江(1982-),男,理學碩士,講師。

