蘇教版初中數學二次函數最值問題解法

江蘇省常州市新北區實驗中學 潘麗琴

蘇教版初中數學二次函數最值問題解法

江蘇省常州市新北區實驗中學 潘麗琴

二次函數是初中數學的重要內容，特別是它的最值問題，更是教師“教”與學生“學”的重難點。筆者通過調查法、歸納總結等方法，對蘇教版初中數學二次函數最值問題的解法進行了歸納，以期學生能夠從容不迫地面對、解決二次函數的最值問題。

蘇教版；二次函數；最值問題；解法

二次函數的最值問題是初中數學教學的重難點，而大部分學生在面對“二次函數最值問題”的時候，往往找不到“著手點”，導致思維不暢，進而影響學生學習的質量，長此以往，同樣不利于學生樹立學好數學的自信心。為了拓展學生的思維，鍛煉和提升學生的分析能力和解題能力，實現“柳暗花明又一村”，筆者舉例說明了常用的解法，具體如下：

一、換元法

二次函數最值問題已經成為當前中考的熱點之一，它出現在試卷中的樣式呈現多樣性，因此，作為一線的教育工作者，要充分發揮自身的引導和指導作用，讓學生掌握解決最值問題的方法，從而抓住著手點，輕松解決問題。這樣不僅能夠提高學生學習數學的自信心，還能夠拓展學生的思維。通過研讀中考試卷發現，其中有一類題目考查的知識點確實是“二次函數”，但是從表面來看，其涉及很多未知量，導致學生迷茫，找不到解決途徑。

【評注】從表面來看，題目中含有3個未知數，求含3個未知數的代數式的最小值。巧妙運用“換元法”，將其轉化成為有關未知數的二次代數式，之后構建二次函數，利用函數的相關性質求取最小值。這里需要特別注意的就是t的取值范圍。

二、圖形法

圖形法又被稱之為“數形結合法”，它往往是根據問題的已知條件和結論之間的內在聯系，從而將數量關系與空間形式巧妙地結合起來，進一步根據這種“結合”，抓住題目解決的“切入點”，形成解題思路，從而準確、快速地解決問題。但是由于受到各種因素的影響，學生一般會忽視“圖形法”，甚至認為作圖是一件非常費力的事情，導致“圖形法”未能物盡其用。新課改背景下，教育工作者要抓住機遇，引導學生認識到“圖形法”的價值和意義，幫助學生擺脫不正確的思想觀念，且能夠在實踐中合理運用該方法，提高自身的解題效率，同時提高自身的正確率。

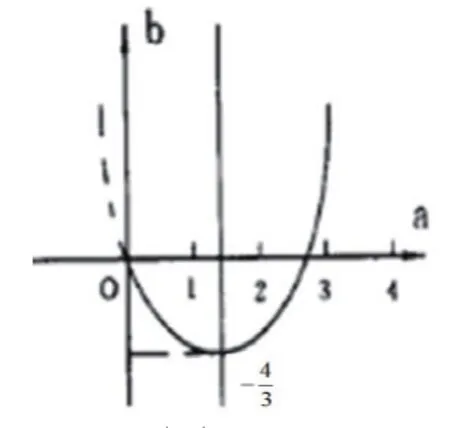
圖1

【評注】要想順利解決該類題目，首先要將問題轉化成為求取“b”的最大值與最小值；其次就是根據題意化簡，得到然后結合二次函數的相關知識點，畫出簡圖，求得“b”的最大值與最小值。乍看之下，這類題目并不是二次函數的最值問題，但實質仍舊是二次函數的最值問題，同時還考查了學生對于“圖形法”的掌握情況。

三、配方法

配方法又被稱之為“公式法”。結合二次函數的相關性質可以歸納出：對于二次函數皆為常數，且y有最大值，且考試中，往往會將其置放于實際問題中，讓學生利用二次函數的相關性質解決實際問題，從而鍛煉和提高學生利用知識解決實際問題的能力。

例3 某一個玩具廠計劃生產一種玩具兔子，每天最高的生產量為40只，且每日生產的兔子能夠全部售出。已知生產x只兔子的成本為R（元），每只玩具兔子的售價為P（元），并且R與x的關系式為R=500+30x，P與x的關系式為P=170-2x。求：

（1）當日產量為多少時，日獲取利潤可以得到1750元？

（2）當日產量為多少時，可以獲取最大利潤？最大利潤是多少元？

【分析】面對該類型題目，首先應該構建一個以“x”為自變量的函數，結合題意可以得出：結合二次函數的相關形式，函數具有最大值，通過配方法可以得到：可以得到日產量為35只時，可以獲得最大利潤，且最大利潤為1950元。

【評注】遇到實際問題時，要結合題意構建二次函數，根據“配方法”可以求得最值。

二次函數最值問題是初中數學的重難點，但是通過歸納總結可知二次函數最值問題的解決方法還是有規律性的，解決問題中，往往會運用到換元法、圖形法以及配方法，為高中階段的進一步學習奠定良好的基礎。作為一線的教育工作者，要認識到初中生的生理和心理特征，充分發揮自身的引導和指導作用，及時做好解法的歸納工作。

[1]梅寧寧．初中數學最值問題的解法探究[J]．寧波教育學院學報，2016（06）．

[2]趙秀琴． 初中數學最值問題的解法[J]．考試周刊，2012（44）．

[3]廖青馨．初中二次函數典型題的解題技巧[J]．經營管理者，2016（30）．