導引頭自適應導彈自旋方法研究*

曹爾聰, 周立勇, 朱鐵勇, 梁曉瑜, 胡小波

(北方光電股份有限公司, 西安 710043)

導引頭自適應導彈自旋方法研究*

曹爾聰, 周立勇, 朱鐵勇, 梁曉瑜, 胡小波

(北方光電股份有限公司, 西安 710043)

導彈彈體轉速變化范圍較大,會給導引頭有效跟蹤目標帶來困難。為消除彈體轉速變化對導引頭跟蹤目標的影響,文中提出一種導引頭自適應彈體轉速的設計方法。這種設計方法不但可以在彈體轉速變化的情況下實時提供正確的目標方位信息,而且可以有效提高導引頭的進動效率,實現導引頭在自旋彈體下消除轉速變化對其影響,達到導引頭精確跟蹤目標,保證導彈命中精度的目的。

導引頭;控制;彈體轉速;自適應

0 引言

導引頭制導系統基本分成兩種控制方式,一種是在彈體不旋轉條件下的控制方式,這種方式中導引頭在任意時刻目標的方位信息相對于大地坐標系是固定的。另一種是彈體在旋轉條件下的控制方式,這種方式導引頭在任意時刻目標的方位信息相對于大地坐標系是跟隨彈體旋轉而變化的,并且變化規律與導彈的自旋密切相關。

根據彈道設計,不同的藥號、裝藥量,以及不同的發射環境等條件(如海拔高度導致空氣密度的變化),均可導致導彈制導段飛行速度變化范圍較大。在導彈的空氣動力設計固定條件下,對于自旋的導彈,決定彈體轉速的一般是彈的飛行速度[1]。導彈在制導段飛行速度變化時,導彈的自旋轉速也會發生變化。導引頭如果不能對變化較大的彈體自旋轉速做出正確的反映,就無法有效的跟蹤目標,將會對導彈的命中精度產生影響。

1 自旋彈慣用處理方法

對于自旋的制導武器,為了保證導引頭能夠反映正確的視線角速度,一般通過旋轉探測器的方法改變進動線圈與探測器的機械方位,以采用固定超前角的方法適應彈體的轉速。以某型導彈導引頭為例,采用固定超前角的方法適應彈旋轉的導引頭各部件的相對位置圖見圖1。由圖1可以看出,導引頭的探測器的刻劃線位置相對于進動線圈的正方向位置沿逆時針旋轉了47°,導引頭的自旋方向從導引頭前端面方向看是逆時針旋轉。彈體旋轉的速度標稱值為6.6 r/s。

由于激光導引頭按照激光照射編碼周期工作,在每個激光編碼周期對陀螺施加的進動力矩的時間為40 ms。當導引頭捕獲目標后,導引頭在40 ms內對陀

螺產生的進動力可以用以下公式表示:

俯仰方向為:Y=A·sin(ωt+θ-47°)

(1)

偏航方向為:X=A·cos(ωt+θ-47°)

(2)

式中:ω為2π×6.6(彈體旋轉的轉速為6.6 r/s);A為導引頭進動的幅值;θ為捕獲目標相對于慣性坐標系的位置方位角。

為了闡述方便,此時捕獲的目標相對于慣性坐標系的位置在偏航正方向的坐標軸上。坐標位置歸一化后的坐標為(1,0),進動力歸一化后的值為坐標位置的均方根。對于位置坐標為(1,0)的進動力為1。

由式(1)、式(2)并不能充分的表達出導引頭的實際進動效果,利用進動力與導引頭進動時間的乘積可以表達實際的進動效果。對于坐標為(1,0)的理想進動效果為1×0.04,即為0.04。實際的進動效果分為兩個方向,偏航方向為:

(3)

俯仰方向為:

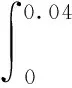
(4)

式中：ω為2π×6.6;θ為捕獲目標相對于慣性坐標系的位置方位角;捕獲的目標相對于慣性坐標系的位置方位坐標為(1,0)。因此θ為0°。

偏航方向,由式(3)可以得到:

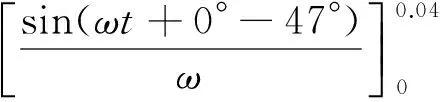
(5)

俯仰方向,由式(4)可以得到:

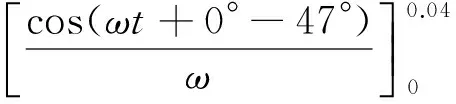
(6)

使用預置超前角的方法,從實際的進動效果上看,在俯仰方向上的進動積累效應為零,其理想進動狀態是在俯仰方向上沒有進動;在偏航方向上的進動也沒有達到理想的進動效果0.04的值,也就是損失了11.8%的進動效果。

當彈的轉速不固定為6.6 r/s,而是上下進行浮動,那么在俯仰與偏航的實際效果與理想進動效果比較值見表1。

由表1可以看出當轉速偏離6.6 r/s時,理想俯仰進動效果誤差率隨偏離值變大而變大。而實際的偏航進動效果也沒有和理想的進動效果一致,并有衰減。并且隨轉速的偏移輸出的進動角速度和需要真實目標輸出的角速度值誤差增大,造成導引頭不能真實反映目標特性,進動的效率大大降低,從而影響到導引頭的歸零時間、品質因數、跟蹤角速度等重要參數,最終影響到導彈的命中精度。因此,固定超前角適應導彈轉速的方法,雖然能夠解決某個固定旋轉速度下的導引頭跟蹤問題,但適應的范圍狹窄,進動效率不夠高[2]。

表1 固定超前角方法在不同轉速下俯仰與偏航的實際進動效果與理想進動效果比較

2 自適應處理方法

該方法基于解決導引頭在彈旋轉的條件下,導引頭仍能夠正確反映目標特性。導彈在飛行的某一時刻,導彈與目標的相對位置或視線角速度在慣性坐標系下是唯一的,并不隨著導彈的旋轉而變化,而導引頭的功能也是為導彈提供正確的目標位置或視線角速度。將導引頭識別目標的位置或視線角速率從彈體旋轉的坐標系下剝離,始終直接映射到慣性坐標系下,用此來驅動光軸指向,從而保證導彈飛行中任意時刻與目標的相對位置或視線角速度在慣性坐標系下與導引頭的指向一致[3]。

為了實現以上的目的,需要做兩步工作。

①取消導引頭的預置超前角,即將導引頭探測器的刻劃線與進動線圈的位置重合(見圖2)。

②增加半導體慣性器件或滾轉陀螺儀獲知導彈的轉速信息。

假設導引頭進動40 ms的初始時刻探測到目標的位置與彈軸的偏差角為θ,此時就是導彈與目標的相對位置或視線角速度在慣性坐標系下的坐標。歸一化后的坐標位置為(cosθ,sinθ),由半導體慣性器件或滾轉陀螺儀輸出的角速度為ω。導引頭輸出進動角速度歸一化的幅值為1,則偏航進動角速度為:

ωx=1·cos(ωt+θ)

(7)

俯仰進動角速度為:

ωy=1·sin(ωt+θ)

(8)

為了分離出θ,將ωt移入到式(7)、式(8)中得到:

1·cos(ωt+θ-ωt)=1·cos(ωt+θ)·cos(ωt)+

1·sin(ωt+θ)·sin(ωt)=1·cosθ

(9)

1·sin(ωt+θ-ωt)=1·sin(ωt+θ)·cos(ωt)-

1·cos(ωt+θ)·sin(ωt)=1·sinθ

(10)

通過移入式(9)、式(10)可以獲得導引頭在慣性坐標系的歸一化坐標(cosθ,sinθ)。因此,只要獲知導彈的旋轉速度,將導彈的轉速信息引入到導引頭進動坐標位置的計算中,從理論上是可以將彈旋轉的因素從導引頭進動角速度計算中剔除,從而達到自適應彈旋轉的功能。

為了實現以上的目的,需要從半導體慣性器件或滾轉陀螺儀獲知導彈的轉速。半導體慣性器件或滾轉陀螺儀輸出的轉速信息以模擬量的形式發送出來。模擬量的大小與轉速的大小成正比關系。cos(ωt)、sin(ωt)的時間起始點可以以接收到激光編碼信號的瞬間時刻為準。自適應算法的流程框圖如圖3所示,可以實現以上算法。

通過正弦發生器和相移形成正、余弦信號,控制正、余弦信號。同步器與激光編碼信號的瞬間時刻同步,正弦的頻率與半導體慣性器件或滾轉陀螺儀輸出的模擬量大小成正比從而和轉速成正比[4]。同時組合乘法器和加法器及減法器并引入偏航與俯仰進動角速度信號,生成新的進動角速度信號。新的角速度信號對應的坐標系始終與慣性坐標系的角偏差一致。

3 自適應方法實現

為了使導引頭實現自適應彈轉速大范圍變化必須引入姿態陀螺儀輸出的彈轉速信息。在導引頭的控制回路的前向通道中必須增加這一環節來實現算法。圖4是加數字算法的導引頭回路框圖,圖中θi(t)為導引頭到目標的視線角;θ0(t)為位標器光軸的角位置;Δθ為視線誤差角;G1為前向傳遞函數,增益為K1;G2為力矩器或驅動線圈傳遞函數,增益為KL;G3為陀螺傳遞函數,增益為KH;UOK1、UOK2分別為偏航、俯仰的進動角速度信號。

進動角速度的表達式為:

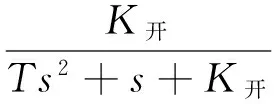
(11)

式中:UOK是導引頭控制小回路的輸出信號;K開是開環增益,K開=K1·KH·KL。

因為增加的環節在導引頭控制回路中,不能影響原有的傳遞關系,所以新增放大環節的增益為1,才能不影響系統的開環增益。因此,在設計該環節時應盡量提高計算的速度和對激光脈沖編碼初始時刻的判斷速度,減少該環節的純延遲時間。在設計電路時,應將電路的截止頻率超過原系統截止頻率5倍以上,或者在軟件中增加超前滯后環節消除電路環節的影響[5]。在數字計算環節中,放大系數應為1。因此,對軟件編寫時,應保證計算結果的模為1。

在A/D采樣和數字計算環節中需要增加一路A/D采樣獲知彈的轉速。導引頭在每個激光編碼周期對陀螺施加的進動力矩的時間為40 ms。導彈的頻響在2 Hz以下,導引頭進動的頻率的截止頻率與導彈的頻響相差12.5倍以上,在制導段內飛行的環境相對平穩,相對于出炮口和導彈加速的階段來說過載不大,因此,在40 ms的時間段內導彈轉速的突變可能性基本為零。基于這一點,可以認為在每個激光編碼周期的進動力矩作用時間40 ms內彈的轉速不變。在每個激光編碼周期內,進動力矩開始作用之前,需要對轉速進行多次采集并平均,當開始進動時就不再采集,而使用進動前的平均值參與整個進動過程的計算。為了便于計算,對于正、余弦的產生采用查表的方法,步進為0.1 Hz。在每一個頻率下每1 ms生成一個數。

為了驗證以上方法是否能達到目的。沿用考核固定前置角適應導彈轉速使用進動效果的方法考核。

在偏航方向理想的進動效果為0.04,理想的俯仰進動效果為0。

用數字計算的方法計算偏航方向的進動效果為:

偏航方向進動效果=0.001·[cos(ω·0+θ)·

cos(ω·0)+sin(ω·0+θ)·sin(ω·0)]+

0.001·[cos(ω·0.001+θ)·cos(ω·0.001)+

sin(ω·0.001+θ)·sin(ω·0.001)]+…+

0.001·[cos(ω·0.039+θ)·cos(ω·0.039)+

sin(ω·0.039+θ)·sin(ω·0.039)]

(12)

式中ω為2π×6.6。

俯仰方向的進動效果為:

俯仰方向進動效果=0.001·[sin(ω·0+θ)·

cos(ω·0)-cos(ω·0+θ)·sin(ω·0)]+

0.001·[sin(ω·0.001+θ)·cos(ω·0.001)-

cos(ω·0.001+θ)·sin(ω·0.001)]+…+

0.001·[sin(ω·0.039+θ)·cos(ω·0.039)-

cos(ω·0.039+θ)·sin(ω·0.039)]

(13)

式中ω為2π×6.6。

轉速為6.6 r/s時,坐標位置在偏航正方向的坐標軸上。θ為捕獲的目標相對于慣性坐標系的位置方位角。這時θ為0°。

經式(12)、式(13)計算獲得的進動效果分別為:

偏航方向的進動效果:0.039 9

俯仰方向的進動效果:8.0×10-6

對于θ為0°時進動效果與理想的進動效果是一致的,那么對于不同的角度又如何呢?以轉速6.6 r/s為例,使用式(12)、式(13),代入不同的彈體轉速,研究偏航與俯仰的進動效果。表2顯示的是不同轉速的進動效果情況。

由表2可以看出,對于不同的轉速,通過數字計算,偏航進動效果誤差率與理想俯仰進動效果誤差率基本為零。因此,可以看出用數字計算方法得到的進動效果與理想的進動效果對比,無論在俯仰還是在偏航方向上完全滿足精度要求。

表2 自適應轉速方法在不同轉速下俯仰與偏航的實際效果與理想進動效果比較

4 結論

采用自適應轉速的方法,可以剔除彈轉速對導引頭跟蹤目標的影響。通過計算,在不同的彈速下,無論是在俯仰還是在偏航方向,導引頭在整個進動過程中都能夠實時的反映出正確的目標方位,大大提高導引頭的實際進動效能,同時也能夠提高導引頭在歸零時間、品質因數、跟蹤角速度等重要方面的性能,從而保證導彈的命中精度。此方法在導引頭半實物仿真及靶試飛行試驗中均得到了驗證,并取得良好結果。在實際應用中還必須考慮滾轉陀螺儀的輸出精度、線性度、溫度零漂等對解算結果的影響。

[1] 鄒汝平, 張延風. 旋轉導彈自旋頻率設計 [J]. 兵工學報, 2007, 28(2): 220-222.

[2] 高長生, 張研, 魏鵬鑫, 等. 質量矩控制自旋彈彈體性能分析 [J]. 飛行力學, 2013, 31(1): 61-64.

[3] 高慶豐, 夏群力, 方蜀州, 等. 一種單通道旋轉導彈自動駕駛儀設計方法 [J]. 北京理工大學學報, 2011, 31(6): 670-674.

[4] 李友善. 自動控制原理 [M]. 北京: 國防工業出版社, 2005: 50-53.

[5] 劉興堂. 導彈制導控制系統分析、設計與仿真 [M]. 西安: 西北工業大學出版社, 2005: 22-28.

ResearchonSelfAdaptiveMissileSpinMethod

CAO Ercong, ZHOU Liyong, ZHU Tieyong, LIANG Xiaoyu, HU Xiaobo

(North Electro-Optic Co. Ltd, Xi’an 710043, China)

The change of projectile speed is difficult to track the target effectively. To eliminate the projectile speed changes affect seeker tracking target. An adaptive method is presented for the large range of projectile speed change. This method can not only under the projectile speed variation in real time to provide accurate information on the range, and effectively improve the efficiency of precession of seeker. Realize the seeker in the projectile spin eliminate change speed of its effects, precise tracking target, ensure the missile accuracy.

seeker; control; missile spin self; adaption

E932.2

A

2016-11-13

曹爾聰(1971-),女,陜西涇陽人,研究員,碩士,研究方向:精確制導控制技術。