幾類特殊曲面曲線的法曲率測地曲率和測地撓率的計算

黃 瑞

(阜陽師范學院 數學與統計學院，安徽 阜陽 236037)

幾類特殊曲面曲線的法曲率測地曲率和測地撓率的計算

黃 瑞

(阜陽師范學院 數學與統計學院，安徽 阜陽 236037)

特殊曲面曲線是曲面論中的一個重要研究對象，坐標曲線、漸近曲線、曲率線和測地線是曲面上常見的幾類特殊曲面曲線，而法曲率、測地曲率和測地撓率又是曲面曲線的三個重要的數字特征。本文首先推導出法曲率、測地曲率和測地撓率的性質；其次，列舉了三者之間最常見的幾種關系；最后，給出上述幾類特殊曲面曲線的法曲率、測地曲率和測地撓率的計算公式。

曲面曲線；法曲率；測地曲率；測地撓率

對曲面曲線的研究是經典微分幾何中曲面論中非常重要的一部分內容，而特殊的曲面曲線，如坐標曲線、漸近曲線、曲率線和測地線又是我們研究的重中之重，研究內容主要包括它們的曲率、撓率、法曲率、測地曲率、測地撓率等。曲面曲線的測地曲率在曲面的保長對應下是保持不變的，它屬于曲面的內蘊幾何學研究的內容，其計算公式的推導有許多不同的方法，[1]利用曲面論基本方程進行推導，[2]給出了直接的推導方法，但過程復雜且計算量大，[3-5]給出了曲面在正交坐標曲線網下計算測地曲率的Liouville公式的證明方法。本文列舉了法曲率、測地曲率和測地撓率之間最常見的三種關系，并由此得到曲面上的直線、漸近曲線、曲率線和測地線的法曲率、測地曲率、測地撓率的計算公式，而坐標曲線的法曲率、測地曲率、測地撓率的計算公式則由定義推導出來。

1 法曲率、測地曲率和測地撓率的計算與性質

1.1 法曲率

證明 由歐拉公式（1），（2）顯然成立，下證（3）。

若P為臍點，則，結論成立。

下設P為非臍點，若為主方向，則結論成立。現設不是P點處的主方向，由（1）不妨假設落在以P為坐標原點，（第一主方向），（第二主方向）為坐標軸的平面直角坐標系的第一象限和第四象限，若記，則，由歐拉公式得

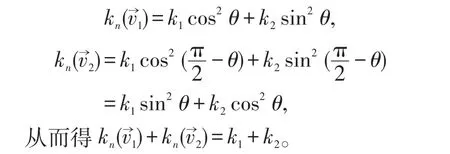
注：在P點的切平面上，以P為坐標原點，（第一主方向），（第二主方向）為坐標軸建立平面直角坐標系，關于對稱指的是所在的直線關于對稱。

1.2 測地曲率

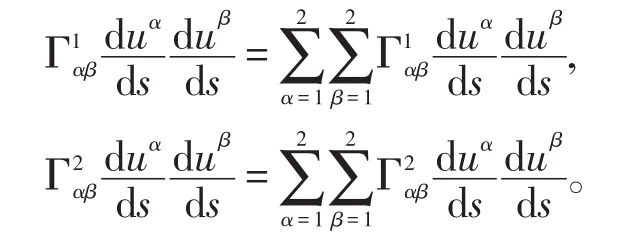
1.3 測地撓率

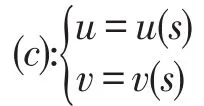
由測地撓率的計算公式知臍點處沿著任意方向的測地撓率都為0，非臍點處沿著主方向的測地撓率為0，即是曲率線的測地撓率恒為0。測地撓率具有類似法曲率的性質。

此定理的證明將在定理5之后給出。

定理3[6]若(c)為曲面上非直線的漸近曲線或測地線，則(c)的撓率等于它的測地撓率。

1.4 法曲率、測地曲率和測地撓率之間的關系

定理4[3]kn2+kg2=k2。

由定理4易見若曲面上存在直線，則直線的法曲率和測地曲率都為0。

特別指出的是，定理5中的θ具有方向性，即從到逆時針轉θ為正角，順時針轉θ為負角，而歐拉公式中出現的是sin2θ和cos2θ，因此無需考慮θ的方向性。

證明 若P為臍點，結論顯然成立。

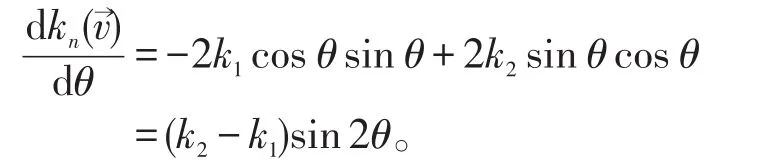
在非臍點P的小鄰域U內取正交的曲率線網作為參數曲線網，記作(u,v)，且不妨設P點沿u-曲線的切方向為第一主方向，則在P處有，從而

在上述特殊的參數系下，定理5中的θ與Liouville公式中的θ是一致的，根據[3]中Liouville公式的證明過程知

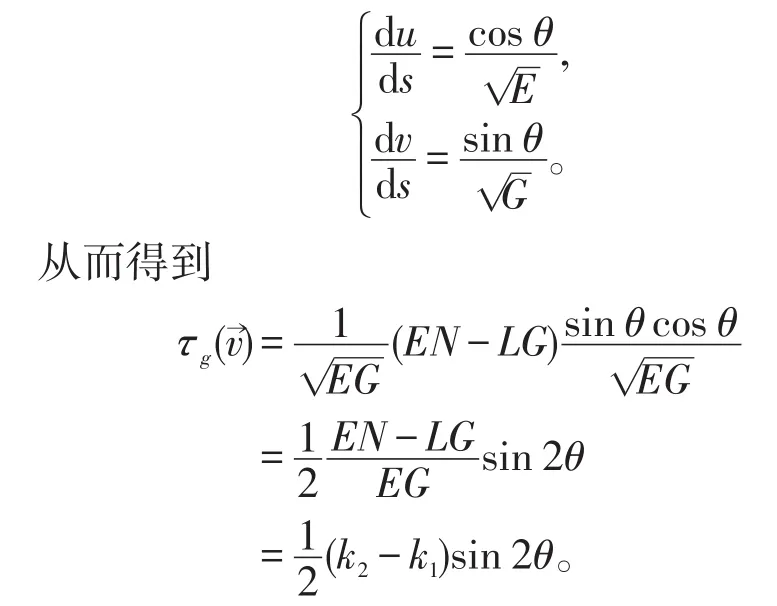
接下來給出定理2的證明。

證明 由定理5知定理2中的（1），（2）顯然成立，下證（3）。

若P為臍點，則，結論成立。

下設P為非臍點，若為主方向，則，結論成立。現設不是P點處的主方向，由定理2（1）不妨假設落在以P為坐標原點，（第一主方向），（第二主方向）為坐標軸的平面直角坐標系的第一象限和第四象限，若記從到的角為θ，則從到的角為由定理5,得

定理6 沿著任意的一條曲面曲線(c)都有成立，其中H,K分別為平均曲率和高斯曲率。

2 特殊曲面曲線的法曲率、測地曲率和測地撓率

2.1 漸近曲線

根據定理3,4，6易得下面的結論。

定理7 設(c)為S上的漸近曲線，若

（1）(c)為直線，則(c)的

（2）(c)不是直線，則(c)的，其中k,τ分別為(c)的曲率和撓率。

由定理7易見可展曲面上的漸近曲線必為平面曲線。

2.2 曲率線

由定理4易得下面的結論。

定理8 設(c)為S上的曲率線，則(c)的法曲率為主曲率，不妨記作，其中k為(c)的曲率。

2.3 測地線

根據定理3,4,6易得下面的結論。

定理9 設(c)為S上的測地線，若

（1）(c)為直線，則(c)的

（2）(c)不是直線，則(c)的kn=±k,kg=0,τg=τ，其中k,τ分別為(c)的曲率和撓率。

由定理9可得曲面上直線的測地撓率未必為零，但平面上的直線以及可展曲面上的直母線都有τg=0，另外若曲面上的測地線為非直線的平面曲線，如球面上的大圓，旋轉曲面上的經線等等，則此測地線的測地撓率為0。

2.4 坐標曲線

證明u-曲線(c)的方程還可以寫作，由于，從而得到

下求(c)的測地曲率，將測地曲率計算公式中的張量記號轉換成高斯記號得到(c)的測地曲率

從而得到(c)的測地曲率

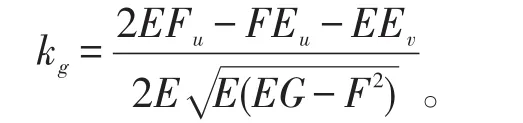
同理可得到下面的定理。

3 結束語

本文首先給出了法曲率、測地曲率和測地撓率的一些“有趣”的性質，如沿著兩個共線的切方向，法曲率和測地撓率都相等，而沿著兩個正交的切方向，法曲率之和為該點處的主曲率之和，測地撓率之和為零。其次總結了法曲率、測地曲率和測地撓率之間的關系，并由此輕松得到直線、漸近曲線、曲率線和測地線這4類特殊曲面曲線的法曲率、測地曲率和測地撓率的計算公式。最后用最原始的定義法得到任意曲面的坐標曲線的法曲率、測地曲率和測地撓率的計算公式，特別地Liouville公式是本文定理10,11中測地曲率計算公式的特例。

[1]梅向明，黃敬之.微分幾何[M].4版.北京：高等教育出版社，2008：146-149.

[2]邢家省，張光照.曲面上曲線的測地曲率向量的注記[J].吉首大學學報(自然科學版)，2013，34（4）：7-10,15.

[3]陳維桓.微分幾何[M].北京：北京大學出版社，2006：229-237.

[4]邢家省，白 璐，高建全.曲面正交網下測地曲率計算公式的推導方法[J].四川理工學院學報(自然科學版)，2015，28（4）：75-79.

[5]羅秀華，張光照，邢家省.曲面正交網下測地曲率和高斯曲率的計算公式的推導方法[J].河南科學，2015，33（7）：1081-1086.

[6]黃 瑞.特殊曲面曲線的性質[J].阜陽師范學院學報(自然科學版)，2016，33（3）：8-11.

Calculations of normal curvature,geodesic curvature and geodesic torsion of some special types of curves on surface

HUANG Rui
(School of Mathematics and Statistics,Fuyang Normal University,Fuyang Anhui236037，China)

Special curve on surface is an important research object in surface theory.Coordinate curves,asymptotic line,curvature line and geodesic line are some special curves which are common on surface,while normal curvature,geodesic curvature and geodesic torsion are the three important numerical traits.This paper first derives the nature of normal curvature,geodesic curvature and geodesic torsion,then lists some common relations among the three,and lastly provides the calculation formulas of normal curvature,geodesic curvature and geodesic torsion of the special types of normal curvature.

curve on surface;normal curvature;geodesic curvature;geodesic torsion

O186.1

A

1004-4329（2017）03-023-04

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）03-023-04

2017-06-17

安徽省高校自然科學研究重點項目（KJ2017A341）；安徽省質量工程項目（2014zy138，2015gxk149）；阜陽師范學院質量工程項目（2016JYXM23，2016JYXM25）資助。

黃 瑞(1985- )，女，碩士，講師，研究方向：微分幾何。