三桿張拉整體的結(jié)構(gòu)剛度分析

羅阿妮，伍承旭，劉賀平

(哈爾濱工程大學(xué) 機(jī)電學(xué)院，黑龍江 哈爾濱 150001)

三桿張拉整體的結(jié)構(gòu)剛度分析

羅阿妮，伍承旭，劉賀平

(哈爾濱工程大學(xué) 機(jī)電學(xué)院，黑龍江 哈爾濱 150001)

三桿張拉整體結(jié)構(gòu)是張拉整體結(jié)構(gòu)體系的基礎(chǔ)，為了更好的研究張拉整體結(jié)構(gòu)體系的力學(xué)性能，本文對(duì)三桿張拉整體結(jié)構(gòu)剛度影響因素進(jìn)行了研究。根據(jù)張拉整體的構(gòu)型理論，利用Matlab軟件編程，建立了三桿張拉整體結(jié)構(gòu)的數(shù)學(xué)模型以及有限元模型。通過(guò)數(shù)值仿真計(jì)算，分析了在軸向力和扭矩作用下，預(yù)緊力、材料彈性模量以及構(gòu)件截面尺寸對(duì)結(jié)構(gòu)軸向、徑向、扭轉(zhuǎn)變形的影響。由仿真計(jì)算數(shù)據(jù)結(jié)果得出：對(duì)張拉整體結(jié)構(gòu)剛度的主要影響因素是預(yù)緊力，而材料彈性模量、構(gòu)件截面尺寸等影響因素次之，該結(jié)論為改善張拉整體結(jié)構(gòu)剛度提供了一定的理論支持。

張拉整體； 彈性剛度； 幾何剛度； 預(yù)緊力； 彈性模量； 截面尺寸； 平衡矩陣

Abstract：Three- bar tensegrity structure is the basis of tensegrity system. In order to better study the mechanical performance of tensegrity system,the factors that influence the stiffness of a three- bar tensegrity structure were investigated in this study. Matlab software was utilized to establish the mathematical and finite- element models of the three- bar tensegrity structure in accordance with the structural theory of tensegrity. Numerical simulation calculations were performed to obtain the pretightening force; the elastic modulus of material; and the effects of the section size of the structure on axial, radial, and torsional deformation under axial force and torque. The analysis of simulation data revealed that tensegrity structural stiffness is mainly influenced by pretightening force, followed by the elastic modulus of the materials and the sectional size of structural parts. Results provide theoretical support for the improvement of the stiffness of the tensegrity structure.

Keywords：tensegrity structures; elastic stiffness; geometric stiffness; pretightening force; modulus of elasticity; sectional dimension; equilibrium matrix

自上世紀(jì)60年代美國(guó)建筑師Fuller提出張拉整體的概念至今，憑借其優(yōu)越的結(jié)構(gòu)特性，已經(jīng)成為研究熱點(diǎn)之一。Geiger在張拉整體概念的基礎(chǔ)上發(fā)展出了索穹頂結(jié)構(gòu)體系，在建筑領(lǐng)域得到廣泛應(yīng)用[1-5]；國(guó)內(nèi)學(xué)者如袁行飛等提出的環(huán)形張拉整體結(jié)構(gòu)[6]以及羅堯治等構(gòu)建的平板型張拉整體結(jié)構(gòu)[7]等，在張拉整體基本單元基礎(chǔ)上進(jìn)行的拓?fù)溲芯咳〉昧艘恍┻M(jìn)展。

國(guó)內(nèi)外張拉整體結(jié)構(gòu)的研究主要集中于結(jié)構(gòu)的構(gòu)型拓?fù)渖希鴮?duì)于結(jié)構(gòu)力學(xué)性能方面的研究較少。三桿張拉整體結(jié)構(gòu)作為張拉整體結(jié)構(gòu)體系中最為常見(jiàn)、最為基礎(chǔ)的基本單元，大部分的張拉整體結(jié)構(gòu)研究都是在其基礎(chǔ)上發(fā)展起來(lái)。所以三桿張拉整體結(jié)構(gòu)的力學(xué)性能，也將決定著以其為基礎(chǔ)所構(gòu)建更為復(fù)雜的張拉整體結(jié)構(gòu)的力學(xué)性能。本文將研究在軸向外載和扭轉(zhuǎn)力矩的作用下，預(yù)緊力、彈性模量，構(gòu)件截面尺寸對(duì)三桿張拉整體結(jié)構(gòu)的軸向變形、徑向變形和扭轉(zhuǎn)變形的影響，從而獲得提高張拉整體結(jié)構(gòu)剛度的措施，為張拉整體的研究與應(yīng)用提供一定的理論支持。

1 張拉整體結(jié)構(gòu)的數(shù)學(xué)模型

如圖1所示的三桿張拉整體結(jié)構(gòu)，其中3根粗線表示桿構(gòu)件，6個(gè)小圓圈表示節(jié)點(diǎn)，節(jié)點(diǎn)1、2、3之間的細(xì)線表示下端面水平索構(gòu)件，節(jié)點(diǎn)4、5、6之間的細(xì)線表示上端面水平索構(gòu)件，上下端面節(jié)點(diǎn)之間的細(xì)線表示斜索構(gòu)件，h表示結(jié)構(gòu)高度，R表示上下端面的外接圓半徑，φ表示上端面與下端面的相位角。分析該結(jié)構(gòu)的剛度時(shí)，需要各構(gòu)件向量，因此，本文將從節(jié)點(diǎn)矩陣和連接矩陣入手，建立此三桿張拉整體結(jié)構(gòu)數(shù)學(xué)模型。

圖1 三桿張拉整體Fig.1 3- bar tensegrity structure

1.1 節(jié)點(diǎn)矩陣

對(duì)于三桿張拉整體結(jié)構(gòu)，其下端面的三個(gè)節(jié)點(diǎn)坐標(biāo)通式可以表示為

(1)

式中i=1，2，3。

上端面的三個(gè)節(jié)點(diǎn)坐標(biāo)通式可以表示為

(2)

式中j=4，5，6

因此，三桿張拉整體結(jié)構(gòu)的節(jié)點(diǎn)矩陣可以表示為

(3)

1.2 構(gòu)件連接矩陣

在三桿張拉整體結(jié)構(gòu)的數(shù)學(xué)模型中，無(wú)論是桿還是索，都是以一個(gè)節(jié)點(diǎn)為構(gòu)件起點(diǎn)，另一個(gè)節(jié)點(diǎn)為構(gòu)件終點(diǎn)，由此可以列出各個(gè)構(gòu)件與節(jié)點(diǎn)之間的關(guān)系，這個(gè)關(guān)系可以用矩陣表示，并將該矩陣稱為連接矩陣。在連接矩陣中，構(gòu)件起點(diǎn)對(duì)應(yīng)元素為“-1”，構(gòu)件終點(diǎn)對(duì)應(yīng)元素為“1”。

如圖1所示的三桿張拉整體結(jié)構(gòu)，桿構(gòu)件及其兩端節(jié)點(diǎn)具體連接情況如表1所示。

表1 桿構(gòu)件與節(jié)點(diǎn)的連接

(4)

而索構(gòu)件及其兩端節(jié)點(diǎn)情況和索構(gòu)件的連接矩陣分析方法與桿構(gòu)件相同，此處就不再贅述。

1.3 構(gòu)件矢量矩陣

利用節(jié)點(diǎn)矩陣和連接矩陣就可以獲得相應(yīng)構(gòu)件向量。所有桿構(gòu)件組成結(jié)構(gòu)的桿向量矩陣，其表達(dá)形式為

(5)

式中bi(i=1，2，3)表示第i根桿向量。

同理，此三桿張拉整體結(jié)構(gòu)的9根索構(gòu)件向量組成結(jié)構(gòu)的索向量矩陣，其表達(dá)形式為

(6)

式中：si(i=1，0，2，…，9)表示第i根索向量，前6列表示水平索向量，后3列表示斜索向量。

2 張拉整體的結(jié)構(gòu)剛度分析

2.1 結(jié)構(gòu)剛度矩陣

張拉整體結(jié)構(gòu)的結(jié)構(gòu)剛度是反映結(jié)構(gòu)中節(jié)點(diǎn)受力與位移的關(guān)系，因此在對(duì)它進(jìn)行剛度分析時(shí)，其整體的受力變形關(guān)系可以表示為

F=Kδ

(7)

式中：F為結(jié)構(gòu)節(jié)點(diǎn)所受的外載向量，K為結(jié)構(gòu)的剛度矩陣，δ為結(jié)構(gòu)的節(jié)點(diǎn)位移向量。

對(duì)于任意張拉整體結(jié)構(gòu)，除了構(gòu)件材料的力學(xué)性能對(duì)結(jié)構(gòu)剛度有所貢獻(xiàn)外，構(gòu)件內(nèi)部用于維持結(jié)構(gòu)自平衡的初始預(yù)緊力對(duì)結(jié)構(gòu)剛度也起著重要影響。因此張拉整體的結(jié)構(gòu)剛度矩陣K由兩部分組成，即

K=Ke+Kg

(8)

式中：Ke為構(gòu)件材料的力學(xué)性能對(duì)結(jié)構(gòu)剛度的貢獻(xiàn)，稱為彈性剛度矩陣，Kg為預(yù)緊力對(duì)結(jié)構(gòu)剛度的貢獻(xiàn)，稱為幾何剛度矩陣。

2.2 彈性剛度矩陣

彈性剛度矩陣是反應(yīng)構(gòu)件抵抗軸向變形的能力，其主要參數(shù)有彈性模量，構(gòu)件尺寸等，本文采用有限元法，首先從構(gòu)建構(gòu)件單元的彈性剛度矩陣出發(fā)。

圖2 力與位移
Fig.2 Force and displacement

對(duì)于圖2所示以i、j為兩端節(jié)點(diǎn)的構(gòu)件單元，其受力變形關(guān)系如下：

(9)

(10)

(11)

式中：Keij即為構(gòu)件單元彈性剛度矩陣，E為構(gòu)件單元彈性模量，A為構(gòu)件單元橫截面積，lij為單元長(zhǎng)度，α、β以及γ分別為構(gòu)件單元與局部坐標(biāo)系x軸、y軸以及z軸的夾角。

由于每個(gè)構(gòu)件單元的彈性剛度矩陣是基于不同局部坐標(biāo)系下建立起來(lái)的，因此在求取結(jié)構(gòu)彈性剛度矩陣時(shí)，必須引入相應(yīng)的協(xié)調(diào)矩陣進(jìn)行坐標(biāo)轉(zhuǎn)換，坐標(biāo)轉(zhuǎn)換方法如下[8-11]：

(12)

將所有坐標(biāo)系轉(zhuǎn)換后的構(gòu)件單元彈性剛度矩陣求和，Ke即為所求結(jié)構(gòu)彈性剛度矩陣：

(13)

式中n為張拉整體結(jié)構(gòu)的桿數(shù)目。

2.3 幾何剛度矩陣

張拉整體結(jié)構(gòu)幾何剛度反映了構(gòu)件抵抗內(nèi)力方向發(fā)生改變的能力[12]，決定它的重要參數(shù)是構(gòu)件內(nèi)部的初始預(yù)緊力，而獲取初始預(yù)緊力的首要步驟是建立結(jié)構(gòu)的力平衡方程。本文通過(guò)結(jié)構(gòu)中各節(jié)點(diǎn)的受力分析，得到結(jié)構(gòu)的力平衡方程，即

AT=W

(14)

式中：A為結(jié)構(gòu)平衡矩陣[13]，T為結(jié)構(gòu)的構(gòu)件預(yù)緊力向量，W為結(jié)構(gòu)的節(jié)點(diǎn)外載荷向量。

當(dāng)結(jié)構(gòu)所受外載為0時(shí)，結(jié)構(gòu)將處于自穩(wěn)定狀態(tài)，這時(shí)的構(gòu)件內(nèi)力即為其初始預(yù)緊力。通過(guò)求解外載為0時(shí)的平衡方程，即可獲得各構(gòu)件的初始預(yù)緊力。

實(shí)際上，平衡矩陣A存在著N階酉陣、半正定的N×M階對(duì)角矩陣以及M階酉陣[14]：

AN×M=UN×N·SN×M·VM×M

(15)

式中：N代表結(jié)構(gòu)自由度；M代表構(gòu)件數(shù)目，矩陣S的對(duì)角線元素就是AA*及A*A的奇異值，個(gè)數(shù)與平衡矩陣的秩相等，U和V的列組成了平衡矩陣正交的基向量，分別張拉整體結(jié)構(gòu)的位移模態(tài)向量和自應(yīng)力模態(tài)向量。

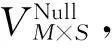
(16)

根據(jù)上式，那么初始預(yù)緊力密度T可以如下表示

(17)

(18)

式中：λ為零空間正交基底的組合系數(shù)向量，其元素可以為任意實(shí)數(shù)。

通過(guò)上述方法即可計(jì)算獲得一組初始預(yù)緊力向量：

(19)

由計(jì)算結(jié)果發(fā)現(xiàn)，由于張拉整體結(jié)構(gòu)的對(duì)稱性，所以同類構(gòu)件的預(yù)緊力相同，T中1～2n行為水平索預(yù)緊力，2n～3n行為斜索預(yù)緊力，3n～4n行為桿預(yù)緊力。其中，n為桿數(shù)目。

在獲得構(gòu)件初始預(yù)緊力密度后，則可以進(jìn)行構(gòu)件單元幾何剛度矩陣的構(gòu)建。與構(gòu)建彈性剛度矩陣時(shí)的受力位移分析相同，構(gòu)件的預(yù)緊力與位移之間的關(guān)系可以表示為

(20)

(21)

式中：Kgij為構(gòu)件單元的幾何剛度矩陣，E為三階單元矩陣，tm為構(gòu)件單元對(duì)應(yīng)的預(yù)緊力，m=1，2，…，n。

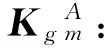
(22)

將所有坐標(biāo)系轉(zhuǎn)換后的構(gòu)件單元彈性剛度矩陣求和，Kg即為所求結(jié)構(gòu)彈性剛度矩陣：

(23)

式中n為張拉整體結(jié)構(gòu)的構(gòu)件數(shù)目。

3 受載仿真計(jì)算分析

本文選用的三桿張拉整體結(jié)構(gòu)數(shù)學(xué)模型的具體結(jié)構(gòu)參數(shù)如表2所示，而力學(xué)參數(shù)可以根據(jù)三桿張拉整體的構(gòu)件自應(yīng)力平衡關(guān)系，按照2.3節(jié)中的方法求得。初始桿力為10 N，水平索力為4.260 N，斜索力為6.093 N。

表2 結(jié)構(gòu)參數(shù)

對(duì)此張拉整體結(jié)構(gòu)分別施加軸向外載與扭轉(zhuǎn)力矩，研究預(yù)緊力、構(gòu)件彈性模量、構(gòu)件尺寸等對(duì)結(jié)構(gòu)的變形影響，而彈性模量在計(jì)算過(guò)程中與橫截面積是乘積關(guān)系，因此本文只作橫截面積的參數(shù)分析。此張拉整體結(jié)構(gòu)在外力的作用下，將發(fā)生軸向變形、端面外接圓直徑的變化、上下端面扭轉(zhuǎn)三種主要變形。下面將對(duì)此結(jié)構(gòu)施加軸向力和扭轉(zhuǎn)力矩，通過(guò)Matlab軟件編程分析，獲得上述三種變形數(shù)據(jù)，研究各參數(shù)對(duì)結(jié)構(gòu)剛度的影響。

首先以上端面三個(gè)節(jié)點(diǎn)為施力點(diǎn)，并沿結(jié)構(gòu)軸線向下的方向施加載荷為20 N，所獲得的分析結(jié)果如表3以及圖3所示。由表可知，在軸向載荷下，隨著預(yù)緊力的增加，軸向位移、徑向位移以及扭轉(zhuǎn)角的變化量都減小。而且在預(yù)緊力增加的初期，各變形量減小趨勢(shì)顯著。

表3小幅增加預(yù)緊力帶來(lái)的位移變化

Table3Aslightincreaseinpreloadresultedindisplacementchanges

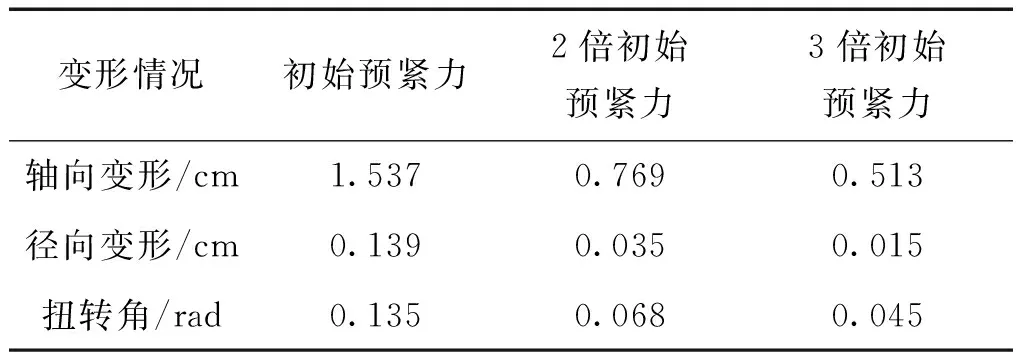
變形情況初始預(yù)緊力2倍初始預(yù)緊力3倍初始預(yù)緊力軸向變形/cm1.5370.7690.513徑向變形/cm0.1390.0350.015扭轉(zhuǎn)角/rad0.1350.0680.045

在進(jìn)一步增大預(yù)緊力的情況下，通過(guò)計(jì)算獲取的位移變形數(shù)據(jù)如表4以及圖4所示，以軸向位移為例，當(dāng)預(yù)緊力由6倍初始預(yù)緊力增加到7倍初始預(yù)緊力，位移變化量?jī)H僅為0.366，因此當(dāng)預(yù)緊力達(dá)到6倍初始預(yù)緊力時(shí)，若繼續(xù)增加預(yù)緊力，那么三類變形的變化敏感度明顯下降。即當(dāng)所有構(gòu)件的預(yù)緊力都超過(guò)外載時(shí)，利用預(yù)緊力的增加來(lái)減小結(jié)構(gòu)各方面變形的效果就不顯著了。

圖3 小幅增加預(yù)緊力對(duì)應(yīng)的變形量Fig.3 A slight increase in preload corresponds to the amount of deformation

Table4Asubstantialincreaseinpreloadresultingindisplacementchanges

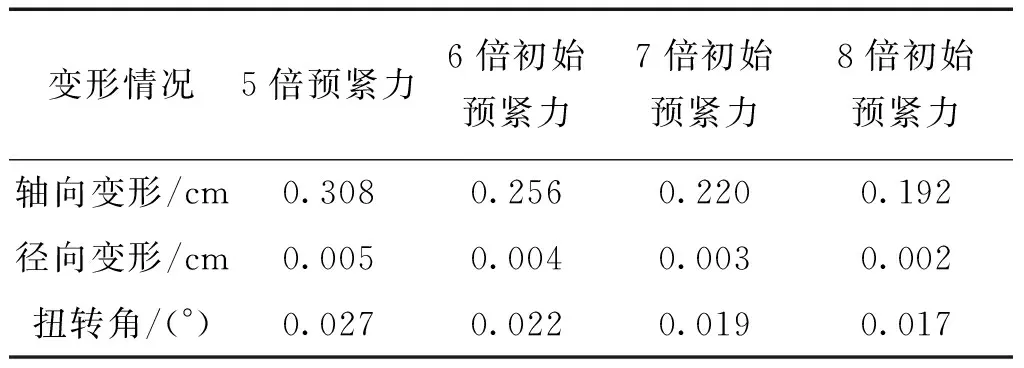
變形情況5倍預(yù)緊力6倍初始預(yù)緊力7倍初始預(yù)緊力8倍初始預(yù)緊力軸向變形/cm0.3080.2560.2200.192徑向變形/cm0.0050.0040.0030.002扭轉(zhuǎn)角/(°)0.0270.0220.0190.017

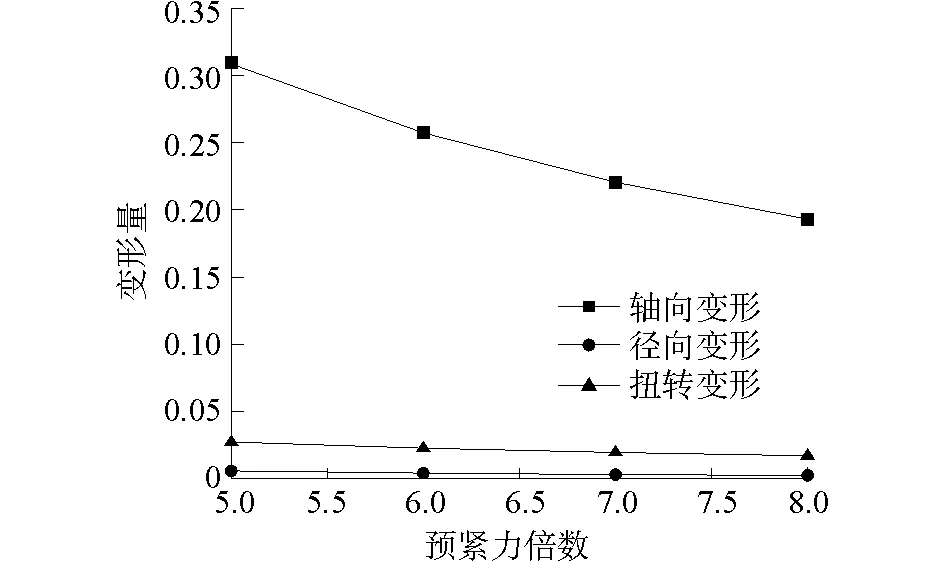
圖4 大幅增加預(yù)緊力對(duì)應(yīng)的變形量Fig.4 A substantial increase in preload corresponds to the amount of deformation

同類構(gòu)件截面變化對(duì)結(jié)構(gòu)變形的影響如表5所示。在軸向載荷下，改變同類構(gòu)件的橫截面積，結(jié)構(gòu)的軸向位移、徑向位移以及扭轉(zhuǎn)角都整體維持在一個(gè)恒定值。因此，在構(gòu)件的彈性變形范圍內(nèi)，三桿張拉整體結(jié)構(gòu)的構(gòu)件截面尺寸的改變對(duì)結(jié)構(gòu)的各方面的剛度影響都很小。在此類載荷的作用下，構(gòu)件的彈性模量對(duì)結(jié)構(gòu)的各方面剛度的影響也很小。

表5改變構(gòu)件截面積情況下的位移

Table5Thedisplacementofthecrosssectionofthecomponentischanged

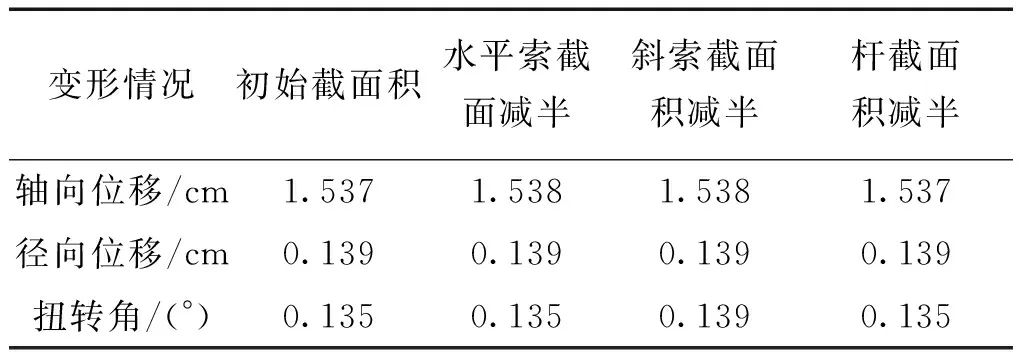
變形情況初始截面積水平索截面減半斜索截面積減半桿截面積減半軸向位移/cm1.5371.5381.5381.537徑向位移/cm0.1390.1390.1390.139扭轉(zhuǎn)角/(°)0.1350.1350.1390.135

按照上面的分析方法，將上端面三個(gè)節(jié)點(diǎn)作為施力點(diǎn)，對(duì)結(jié)構(gòu)施加扭轉(zhuǎn)載荷為3 N·m。通過(guò)分析可知，在扭轉(zhuǎn)載荷作用下，隨著預(yù)緊力的增加，此結(jié)構(gòu)各方向的位移急劇下降，而后下降趨勢(shì)逐漸趨于平穩(wěn)，最后保持定值。這與軸向載荷作用下的預(yù)緊力對(duì)結(jié)構(gòu)剛度的影響類似，此外，在結(jié)構(gòu)位移變化趨于定值時(shí)，也必然存在預(yù)緊力與結(jié)構(gòu)外載之間的數(shù)量關(guān)系，而通過(guò)力與力矩的對(duì)比顯然無(wú)法直觀的反應(yīng)兩者之間的關(guān)系，因此采取將力矩分解為等效節(jié)點(diǎn)力的措施，即上端面每個(gè)節(jié)點(diǎn)承受外力約為6.7 N，總外力為20 N。將扭矩等效為水平節(jié)點(diǎn)力后，再通過(guò)增加預(yù)緊力獲得的數(shù)據(jù)如表6以及圖5所示，當(dāng)預(yù)緊力增加到6倍左右時(shí)，三類位移受預(yù)緊力增大的影響明顯下降，而此時(shí)各構(gòu)件的預(yù)緊力恰好都大于總外力，因此可以得到與軸向載荷情況下同樣的結(jié)論，即只有當(dāng)所有構(gòu)件預(yù)緊力都大于外載荷時(shí)，結(jié)構(gòu)的三類位移趨于定值。

表6等效外載荷為20N時(shí)的位移

Table6Displacementunderequivalent20Nexternalload

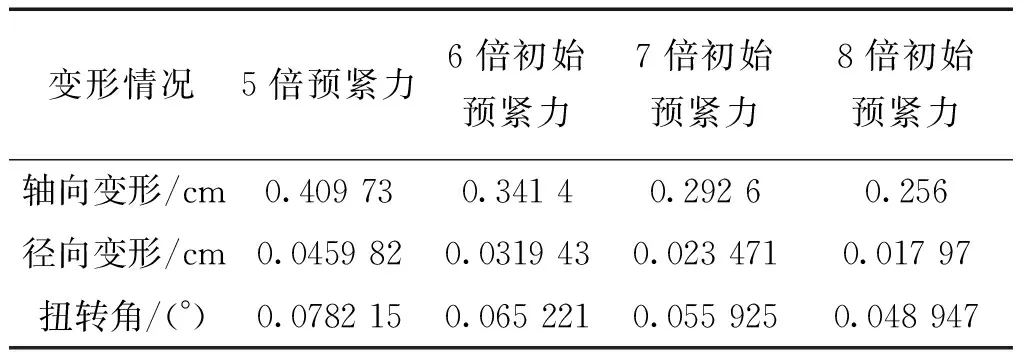
變形情況5倍預(yù)緊力6倍初始預(yù)緊力7倍初始預(yù)緊力8倍初始預(yù)緊力軸向變形/cm0.409730.34140.29260.256徑向變形/cm0.0459820.0319430.0234710.01797扭轉(zhuǎn)角/(°)0.0782150.0652210.0559250.048947

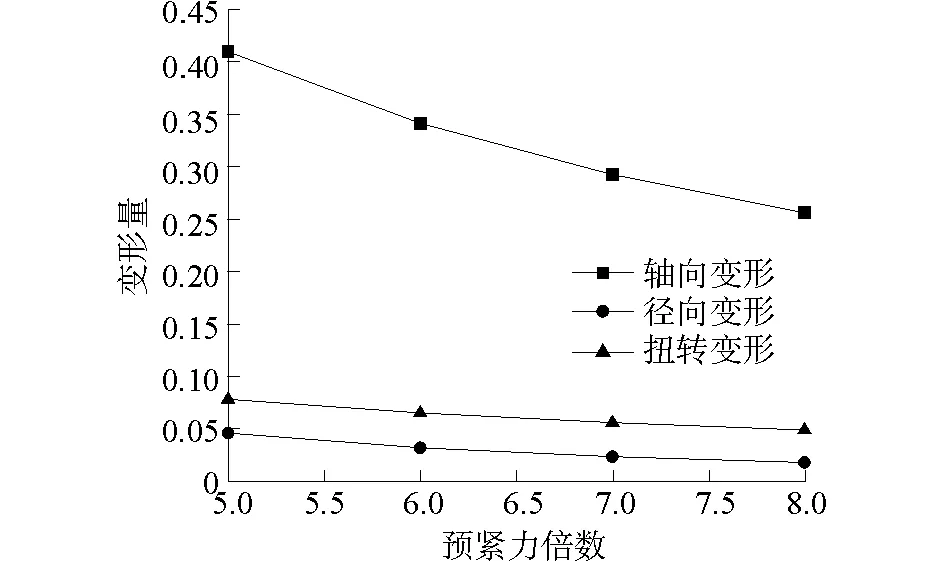
圖5 等效外載為20 N時(shí)的預(yù)緊力與變形量Fig.5 Preload and deformation of equivalent 20 N under external loading

在扭轉(zhuǎn)載荷下，構(gòu)件的橫截面積對(duì)此結(jié)構(gòu)的軸向位移、徑向位移以及扭轉(zhuǎn)角的影響與在軸向載荷下的情況也類似，三類變形幾乎恒定不變。同理，在此類載荷作用下，構(gòu)件彈性模量對(duì)三類變形的影響也可以忽略。

通過(guò)上面計(jì)算結(jié)果分析可知，預(yù)緊力對(duì)三桿張拉整體結(jié)構(gòu)的各方面變形都有顯著影響，構(gòu)件的截面尺寸和彈性模量對(duì)結(jié)構(gòu)各方面的變形的影響卻很小。但是隨著預(yù)緊力逐漸增大，結(jié)構(gòu)各方面變形的變化量也逐漸減小，即預(yù)緊力達(dá)到一定程度時(shí)，預(yù)緊力對(duì)結(jié)構(gòu)剛度的影響逐漸減小，結(jié)構(gòu)剛度幾乎趨于不變，這是由于當(dāng)預(yù)緊力無(wú)限增大，結(jié)構(gòu)的剛化不斷加強(qiáng)，使得整個(gè)結(jié)構(gòu)更趨近于一個(gè)剛性結(jié)構(gòu)，對(duì)于一般的剛性結(jié)構(gòu)而言，彈性剛度為結(jié)構(gòu)的唯一剛度，而要顯著改變“剛性”張拉整體結(jié)構(gòu)的剛度勢(shì)必要使預(yù)緊力發(fā)生與彈性剛度相同數(shù)量級(jí)的改變，顯然這是不明智的，且索的抗拉強(qiáng)度、桿的抗壓強(qiáng)度也面臨著挑戰(zhàn)。

4 結(jié)論

1)預(yù)緊力對(duì)張拉整體結(jié)構(gòu)的結(jié)構(gòu)剛度影響很大。隨著預(yù)緊力的增加，結(jié)構(gòu)剛度將增加，其各方面變形將減小。但隨著預(yù)緊力逐漸增加，結(jié)構(gòu)剛度改善的有效性降低。

2)構(gòu)件的彈性模量和橫截面積對(duì)結(jié)構(gòu)剛度貢獻(xiàn)不明顯，即兩者的變化對(duì)此結(jié)構(gòu)各方面變形影響很小。

3)在實(shí)際工程應(yīng)用中，可以通過(guò)增加預(yù)緊力提升張拉整體結(jié)構(gòu)的剛度；同時(shí)，在不影響張拉整體結(jié)構(gòu)剛度的情況下，可以適當(dāng)減小構(gòu)件橫截面積來(lái)達(dá)到減小結(jié)構(gòu)整體質(zhì)量的目的。

[1] GEIGER D, ANDREW S, CHEN D. The design and construction of two cable domes for the Korean Olympics [C]//Shells, Membranes and Space Frames, Proceedings of the IASS Symposium on Membrane Structures and Space Frames, Osaka,1986: 15-19.

[2] HERSKOWITZ M. Dome hits 30: Historic construction covers all bases [R]. Houston Post 1995: B9.

[3] RASTORFER D. Structural gymnastics for the olympics [J]. Architectural record, 1988， 176(10)： 128-135.

[4] 董石麟，袁行飛. 索穹頂結(jié)構(gòu)體系若干問(wèn)題研究新進(jìn)展[J]. 浙江大學(xué)學(xué)報(bào), 2008, 42(1): 1-7. DONG Shilin,YUAN Hangfei.Cable domes on new developments in[J]. Journal of Zhejiang University, 2008, 42 (1): 1-7.

[5] 王澤強(qiáng)，程書(shū)華，尤德清,等. 索穹頂結(jié)構(gòu)施工技術(shù)研究[J]. 建筑結(jié)構(gòu)學(xué)報(bào), 2012, 33(4): 67-76. WANG Zeqiang, CHENG Shuhua, YOU Deqing，et al. Research on the technology of cable dome structure[J]. Construction of building structures， 2012, 33 (4): 67-76.

[6] 袁行飛，彭張立，董石麟.環(huán)形張拉整體結(jié)構(gòu)的研究和應(yīng)用[J]. 土木工程學(xué)報(bào), 2008, 41(5): 8-13. YUAN Hangfei, ZHANG Peng, DONG Shilin. Tensegrity torus of the research and application of[J]. China civil engineering journal, 2008, 41 (5): 8-13.

[7] 羅堯治，董石麟.平板型張拉整體結(jié)構(gòu)幾何體系及受力特性分析[J]. 空間結(jié)構(gòu), 2001, 7(1): 11-16. LUO Yaozhi, DONG Shilin. Analysis of geometric system and mechanical behavior of flat tensegrity structures[J]. Spatial structure, 2001, 7 (1): 11-16.

[8] 徐斌，高躍飛，余龍. Matlab有限元結(jié)構(gòu)動(dòng)力學(xué)分析與工程應(yīng)用[M]. 北京：清華大學(xué)出版社, 70-72. XU Bin, GAO Yuefei, YU Long. Matlab finite element structure dynamics analysis and engineering applications[M]. Beijing: Tsinghua University press, 70-72.

[9] 胡于進(jìn)，王璋奇.有限元分析及應(yīng)用[M]. 北京: 清華大學(xué)出版社, 2009: 4. HU Yujin, WANG Zhangqi. Finite element analysis and application[M]. Beijing: Tsinghua University press, 2009: 4.

[10] 李亞智，趙美英，萬(wàn)小朋.有限元法基礎(chǔ)與程序設(shè)計(jì)[M]. 北京: 科學(xué)出版社, 2004. LI Yazhi, ZHAO Meiying, WAN Xiaopeng. Finite element method and program design[M]. Beijing: Science Press, 2004.

[11] 王煥定，陳少峰，邊文鳳.有限單元法基礎(chǔ)及MATLAB編程[M]. 北京: 高等教育出版社, 2012. WANG Huanding, CHEN Shaofeng, FENG Wen. Finite element method and MATLAB programming[M]. Beijing: Higher Education Press, 2012.

[12] 夏巨偉. 索桿張力結(jié)構(gòu)的預(yù)張力偏差和剛度解析[D].杭州：浙江大學(xué), 2014. XIA Juwei. Cable tension deviation strut structure and stiffness analysis[D].Hangzhou:Zhejiang University, 2014.

[13] 梁銳. 基于平衡矩陣?yán)碚摰膹埨w結(jié)構(gòu)形態(tài)分析[D].成都：西南交通大學(xué), 2013. LIANG Rui. Shape analysis of tensegrity structures based on equilibrium matrix theory[D].Chengdu:Southwest Jiao Tong University, 2013.

[14] 蔣正新，施國(guó)梁.矩陣?yán)碚摷捌鋺?yīng)用[M]. 北京：北京航空學(xué)院出版社, 1988. JIANG Zhengxin, SHI Guoliang. Matrix theory and application[M]. Beijing: Beijing Institute of Aeronautics Press, 1988.

Structuralstiffnessofthree-bartensegrity

LUO Ani, WU Chengxu, LIU Heping

(College of mechanical and electrical engineering，Harbin Engineering University，Harbin 150001，China)

10.11990/jheu.201606086

http://www.cnki.net/kcms/detail/23.1390.u.20170426.1815.092.html

TU399

A

1006- 7043(2017)09- 1450- 06

2016-06-27. < class="emphasis_bold">網(wǎng)絡(luò)出版日期

日期：2017-04-26.

國(guó)家自然科學(xué)基金項(xiàng)目(51605111, 51675114)；中央高校基本科研業(yè)務(wù)費(fèi)專項(xiàng)項(xiàng)目(HEUCFM170701).

羅阿妮(1978-), 女, 副教授； 伍承旭(1991-), 男, 碩士研究生； 劉賀平(1975-), 男, 副教授.

劉賀平，E- mail:liuheping@hrbeu.edu.cn.

本文引用格式：羅阿妮，伍承旭，劉賀平. 三桿張拉整體的結(jié)構(gòu)剛度分析[J]. 哈爾濱工程大學(xué)學(xué)報(bào)， 2017， 38(9): 1450-1455.

LUO Ani, WU Chengxu, LIU Heping. Structural stiffness of three- bar tensegrity[J]. Journal of Harbin Engineering University， 2017， 38(9): 1450-1455.