有限體積法的實體結構疲勞可靠性分析

于艷春，李建操，陳衛東，路勝卓

(1.東北農業大學 水利與土木工程學院，黑龍江 哈爾濱 150030; 2. 滁州學院 地理信息與旅游學院，安徽 滁州 239000; 3.哈爾濱工程大學 航天與建筑工程學院,黑龍江 哈爾濱 150001)

有限體積法的實體結構疲勞可靠性分析

于艷春1，李建操2，陳衛東3，路勝卓3

(1.東北農業大學 水利與土木工程學院，黑龍江 哈爾濱 150030; 2. 滁州學院 地理信息與旅游學院，安徽 滁州 239000; 3.哈爾濱工程大學 航天與建筑工程學院,黑龍江 哈爾濱 150001)

為了提高實體結構系統疲勞可靠性的計算效率,本文采用有限體積法研究了實體結構系統的疲勞可靠性問題。通過依據累積損傷模型對結構元件的疲勞可靠性進行分析，建立了實體結構系統的分析模型，分析了實體結構系統疲勞失效機理和判別方法。本文利用改進的分支限界法搜索了結構系統的主要失效模式，采用簡化的疲勞可靠性分析方法計算了結構系統的疲勞可靠度。通過算例分析，得到的結構系統疲勞可靠度的計算結果在簡單界值法的估算范圍內，且隨著疲勞載荷循環次數的增加可靠度不斷減小。該計算結果的趨勢是正確的、符合客觀實際的，證明了提出方法的正確性，為結構系統疲勞可靠性分析提供理論基礎。

有限體積法； 疲勞可靠性； 結構系統； 失效模式； 累積損傷； 分支限界法； 實體結構； 失效機理

Abstract：In this study, the finite volume method was adopted to analyze the fatigue reliability of a solid structure system and to optimize its computational efficiency. The fatigue reliability of structural elements was analyzed on the basis of the cumulative damage model. The analytical model of a solid structure system was established, and the fatigue failure mechanism of a solid structure system was analyzed. In addition, the recognition of fatigue failure was explored, and the main failure modes of the structural system were investigated through the improved branch- and- bound method. The fatigue reliability of the structural system was calculated through the simplified fatigue reliability analysis method. The analysis of calculation examples revealed that the fatigue reliability of the structure system is within the estimation range of the simple bound- value method. In addition, reliability continuously decreases with increasing fatigue load cycles. The trend of the calculation results was correct and valid, thus validating the method. The proposed method provides a theoretical basis for the fatigue reliability analysis of structural systems.

Keywords：finite volume method; fatigue reliability; structural system; failure mode; cumulative damage; branch- and- bound method; solid structure; failure mechanism

對于工程中大多數結構體系，結構系統破壞的主要形式是結構在疲勞載荷作用下的失效破壞。在現實生活中，有很多結構常年受自然界的各種疲勞載荷的作用，在使用壽命期間內的主要失效形式是疲勞失效，因此，研究結構系統的疲勞可靠性分析意義重大。在國外，Wirsching等基于S-N曲線疲勞損傷分析方法對元件的疲勞可靠性進行了分析[1]。隨后，Stahl等對結構元件的疲勞可靠性研究作了更進一步的分析討論[2-4]。在國內，還有許多文獻在結構系統的疲勞可靠性分析領域做了相關研究[5-10]。張永蒼研究了在對稱循環載荷下的結構系統的疲勞可靠性分析的基本過程。董聰等研究了結構系統疲勞壽命的可靠性分析的基本理論與計算方法，提出了分枝- 約界法。綜上，結構系統的疲勞可靠性分析比結構元件的可靠性分析發展的緩慢，這是由于結構系統疲勞可靠性分析要比結構元件的疲勞可靠性分析復雜的多。由于實際工程中的絕大多數的結構是靜不定結構，結構系統的失效形式非常復雜，如何高效地搜索主要失效模式，同時考慮各個失效模式之間的相關性仍是結構系統的疲勞可靠性分析的難點問題。大多數的疲勞可靠性分析主要針對桁架結構，對于實體結構的疲勞可靠性分析較為少見。因此，本文基于有限體積法對實體結構的疲勞可靠性進行了研究。

1 結構元件的疲勞可靠性研究

1.1 S- N曲線法

S-N曲線是表達載荷應力S與疲勞壽命N之間關系的曲線，在疲勞設計分析中，一般采用確定斜率雙對數線性模型，S-N曲線的表達式為

lgN=lgA-mlgS

(1)

或者

NSm=A

(2)

式中：S為選定的應力范圍水平，N為在確定的應力作用下的疲勞壽命的某一統計特征值，m和A表示材料的常數。

在實際的工程應用中，結構的疲勞損傷累加到一定程度時，結構發生疲勞破壞，即循環載荷作用的時間越長，結構的疲勞累積損傷值在不斷地增大。因此將累積損傷D(n)作為基本參數，則其安全余量方程為

MD=D(n)-Dc≤0

(3)

式中：D(n)為累積損傷，Dc為累積損傷臨界值，這里認為Dc為一常數，且Dc=1。則元件的可靠度可寫成

P=P{D(n)-Dc≤0}

(4)

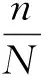
(5)

累積損傷D(n)也可以用對數正態分布來描述，且在相同應力條件下，隨著疲勞載荷循環數的增加，疲勞累積損傷的期望和方差等統計特性也是線性累加的。在常幅載荷作用下，構件的累積損傷是線性變化的。即當t=0時，構件還沒有損傷，累積損傷的期望和方差為零，若一次循環載荷產生的損傷的期望和方差為dE和dD，則在t=n時刻元件累積損傷的期望和方差為dEn和dDn，dE和dD與載荷水平有關。對數正態分布的期望和方差可以表示為

(6)

Var=e(2μ+σ2)(eσ2-1)

(7)

由以上兩式可求出

(8)

(9)

則結構元件在常幅疲勞載荷作用下的疲勞可靠性指標的表達式為

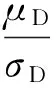
(10)

累積損傷的分布可由疲勞壽命的分布分析得到，即

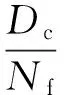
(11)

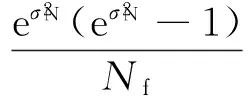
(12)

式中：σN為疲勞壽命的方差，Nf為極限疲勞壽命。

2 結構系統的疲勞可靠性研究

2.1 結構系統的失效機理

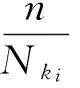
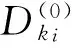
(13)

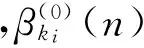
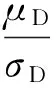
(14)

式中：dE、dD分別為累積損傷的期望和方差，可以通過式(11)、(12)求出。

若假定各結構元件的疲勞失效概率均為同一值Pc，則由式(13)、(14)可以反求出n，即當各結構元件的疲勞失效概率達到某一個相同值時，可以求出每個結構元件所需要的載荷循環數nki。結構元件的nki值越小，則說明該元件可能最先失效。因此，取nki值最小的結構元件作為第一個失效元，并選取nki值在一定范圍內的元件作為第一級臨界失效元。假設元件的最小nki值為nmin，則

C≤nmin/n≤1

(15)

式中C的取值可根據具體分析情況而定。

當確定第一個失效元疲勞失效后，根據疲勞失效的特點，將該失效元從結構系統中去掉，重新對結構系統進行內力分析，可以計算出其他未失效元件的累積損傷和失效概率，同樣也可以求出未失效元件的nki值。取未失效元件中nki值的最小的元件作為下一個失效元，并選取nki值在一定范圍內的結構元件作為第二級臨界失效元。這樣重復計算，直到有m個元件失效后，在結構系統中形成一個臨界破壞截面，該臨界破壞截面的承載能力不斷下降，此時如果計算未失效的元件中最小的nki值小于某一設定值nc時，nc的取值可根據后續失效元件的失效時間而定。此時可以認為其余未失效元件即將在很短的時間內失效，導致該臨界破壞截面的承載能力即將喪失，而整個結構系統的承載能力大幅度降低，不能滿足原有的承載能力，使得結構系統失效。以上過程為本文研究實體結構系統的疲勞可靠性分析的結構系統的失效機理。

2.2 結構系統主要失效模式的搜索

2.2.1 第一級臨界失效元的確定

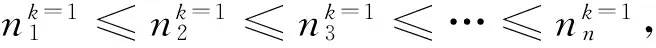
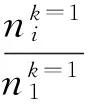
(16)

式中C的取值可根據具體情況分析而定。由于此時結構處于完整的初始階段，通過S-N曲線的表達式(2)可知，元件的內力越大，其疲勞壽命就越小，元件累積損傷的越快，它的破壞概率就越大。因此，可以直接選取一定范圍的內力較大的元件作為第一級的臨界失效元，這樣可以縮減許多工作量。

2.2.2 第k級臨界失效元的確定

假設在疲勞載荷的作用下，有k1、k2、…、kk-1共k-1個結構元件失效，將這k-1個結構元件在結構系統中去掉，內力重新分配，可以求出未失效的元件ki(i=k,k+1,…,N)的疲勞累積損傷值，即

(17)

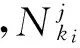
假設又經歷了時間nk，可以由式(13)、(14)計算出未失效元件ki的疲勞可靠性指標和疲勞失效概率。若假定各元件的疲勞失效概率均為同一值Pc，則由式(13)、(14)可以反求出nk，可以取未失效元件中nk值最小的元件作為第k級的失效元，并選取nki值在一定范圍內的結構元件作為第k級臨界失效元。這樣按上述方法重復搜索，直到滿足整個結構系統失效的條件，最終形成系統的一個主要失效模式。

2.3 結構系統的失效概率

考慮到疲勞破壞的特殊性，結構的疲勞破壞是一個時間歷程，認為主要失效模式在同一時間同時發生破壞的可能性很小，即各主要失效模式破壞的共概率很小，近似為零。呂海波等提出了一種簡化的疲勞可靠性分析方法[12]。

假設結構系統含有m個主要失效模式，每一個失效模式的失效概率分別為a1、a2、…、am，ai是當其余失效模式不發生時，第i個失效模式發生的概率。若用事件E1、E2、…、Em分別表示各個主要失效模式發生導致結構系統失效，P1、P2、…、Pm分別為相應的失效概率，則

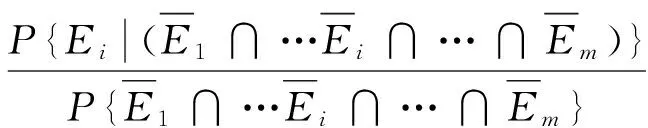
(18)

有以下方程組:

(19)

求解上面的方程組可得到P1、P2、…、Pm，整個系統的失效概率為

Pf=P1+P2+…+Pm

(20)

3 算例分析

3.1 等截面實體結構

如圖1所示的實體結構模型，結構的一端是固定端，另一端是自由端，結構上作用著均勻分布的疲勞載荷F(t)，載荷的形式表示為

F(t)=-1.0×102sin(5.0×103πt)

(21)

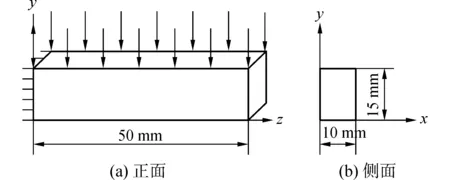
圖1 實體結構模型Fig.1 Calculation model of entity structure

結構的材料參數：密度為7 800 kg/m3、彈性模量為210 GPa、泊松比為0.3，根據文獻[7]選取S-N曲線法中的參數為：m=3.152，A=3.26×1012。這里將結構的疲勞壽命N看作隨機變量，且服從對數正態分布，疲勞壽命的均值通過S-N曲線法進行估算，變異系數取為0.54。將該實體結構采用有限體積法進行網格劃分，共劃分了418實體單元，151個節點。對該實體結構進行結構系統的疲勞可靠性分析。

采用有限體積法對結構系統進行內力分析，求出每個實體單元的最大應力σmax。并選取得到的σmax較大的實體單元作為第一級失效元件及臨界失效元件。由于單元個數較多，只列出部分與分析有關的單元的最大應力值，如表1所示。

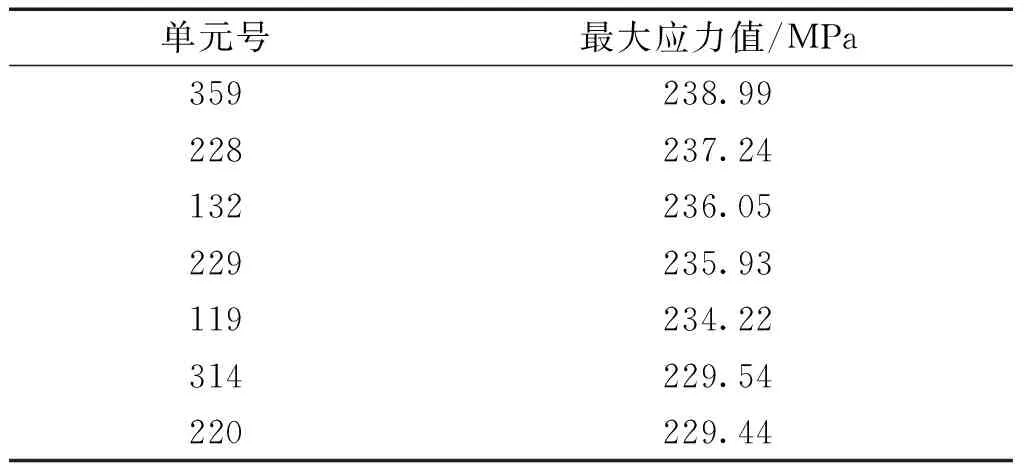
表1 單元的應力值

這里選取實體單元359為第一級失效元，228、132、229、119為第一級臨界失效元。

以單元號229為第一失效元的分支為例，分析失效模式形成的過程。單元229失效后，將單元229從結構系統中去掉，內力重新分配，由前述方法可以求出未失效元件的疲勞可靠性分析參數，由于單元數較多，只列出與分析有關的單元，計算當疲勞失效概率為50%時，單元所需要的載荷循環次數ni的值，見表2。

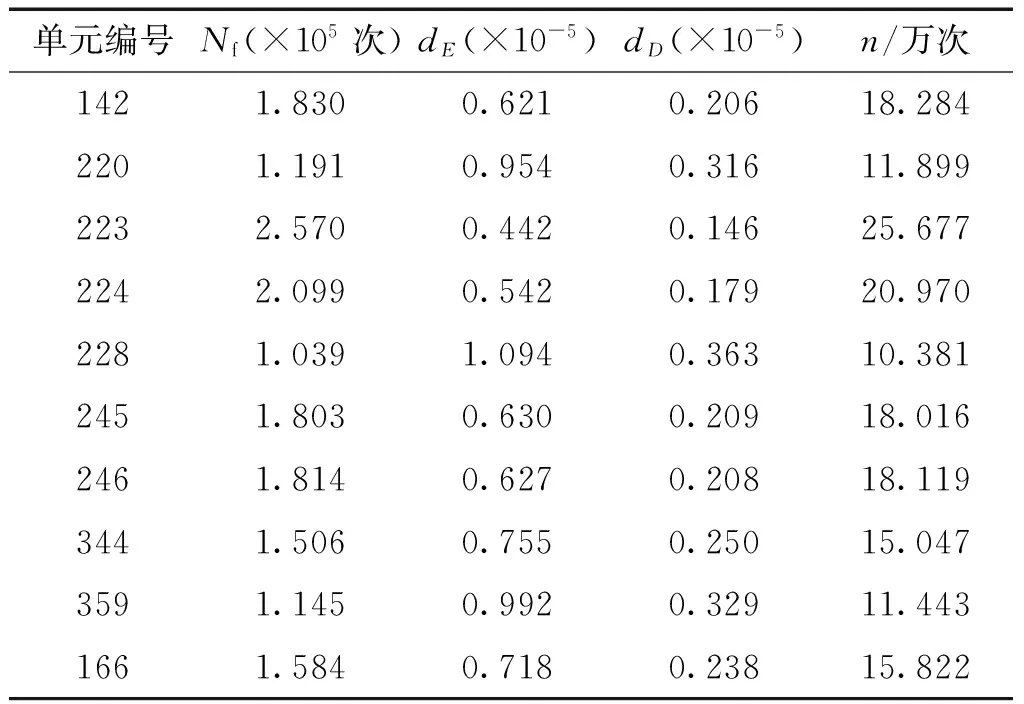
表2 第一級疲勞可靠性參數

從表2中可看出，選取單元228作為第二級失效元。取C=1.02，第二級沒有選取臨界失效元。將單元228從結構系統中去掉，同理可求出未失效元件的疲勞可靠性分析參數見表3。

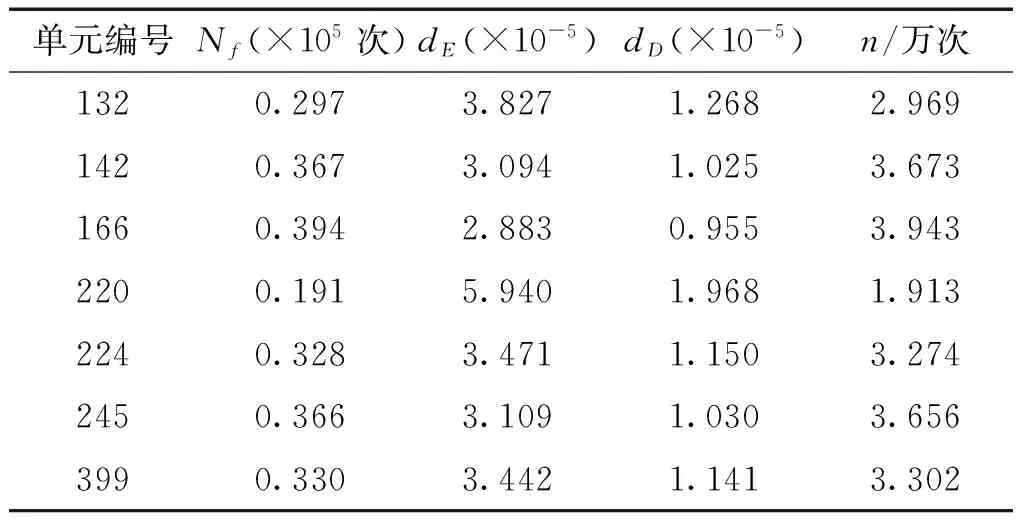
表3 第二級疲勞可靠性參數

由表3可知，選取單元220作為第三級失效元。取C=1.02，第三級沒有選取臨界失效元。同理可求未失效元件的疲勞可靠性分析參數見表4。

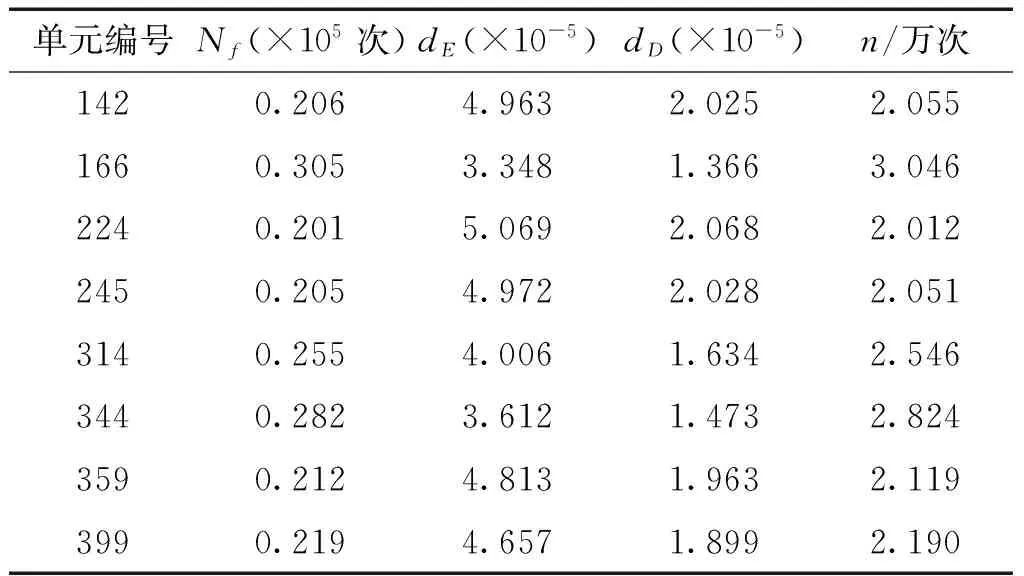
表4 第三級疲勞可靠性參數Table 4 Parameters of fatigue reliability for third stage

從表4的計算結果可看出，n值最小的單元為244，因此，選取單元224作為第四級失效元。取C=1.02，第四級沒有臨界失效元。同理尋找下一級失效元，直到第十級失效單元132失效后，將未失效元的疲勞可靠性參數列于表5中。

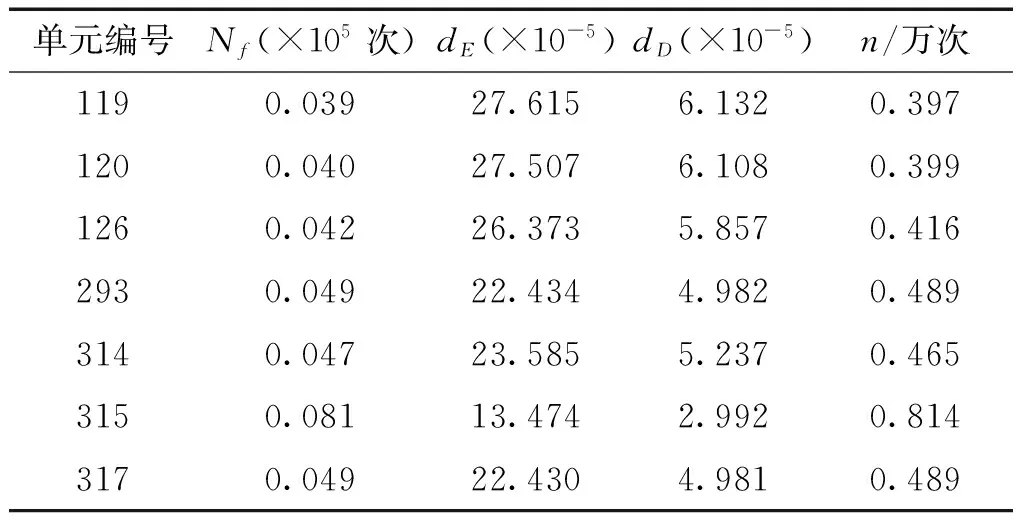
表5 第十級疲勞可靠性參數Table 5 Parameters of fatigue reliability for tenth stage

從表5的計算結果可看出，n值最小的單元為119，因此，選取單元119作為第十一級失效元。取C=1.02，選取單元120作為第十一級臨界失效元。從該計算分支的失效模式的失效路徑可以看出，只有該級包含臨界失效元，其他各級都不含有臨界失效元。同樣將單元119從結構系統中去掉，重新分配，按上述方法繼續搜索下一級失效元，直到計算到第十四級失效元314失效后，計算未失效元的疲勞可靠性參數，計算結果列于表6中。

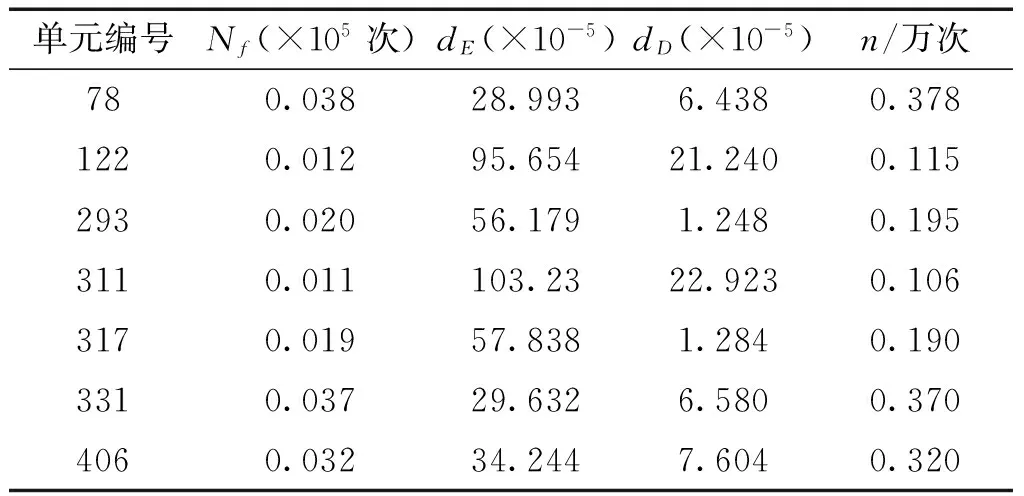
表6 第十四級疲勞可靠性參數Table 6 Parameters of fatigue reliability for fourteeth stage

由表6可知，選取單元311作為第十五級失效元。取C=1.02，第十五級沒有臨界失效元。同理可求未失效元件的疲勞可靠性分析參數見表7。

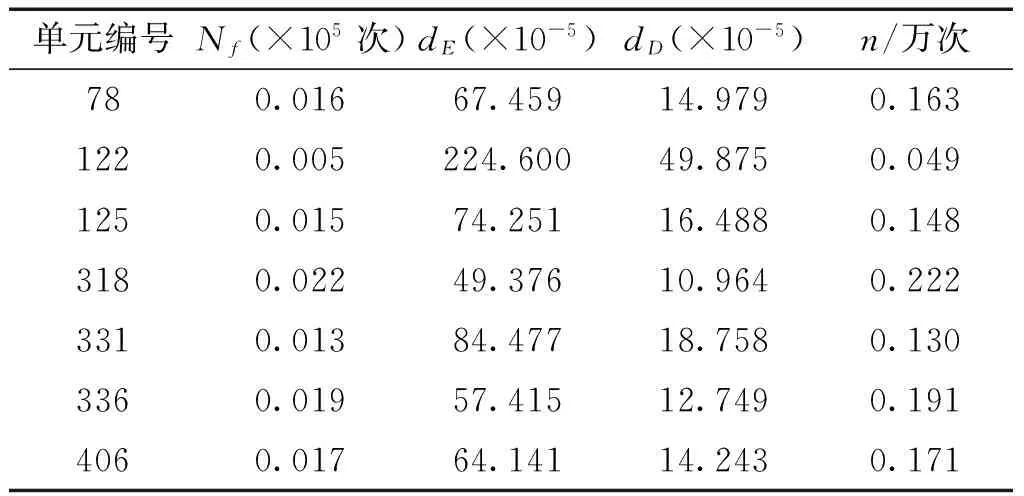
表7 第十五級疲勞可靠性參數Table 7 Parameters of fatigue reliability for fifteenth stage

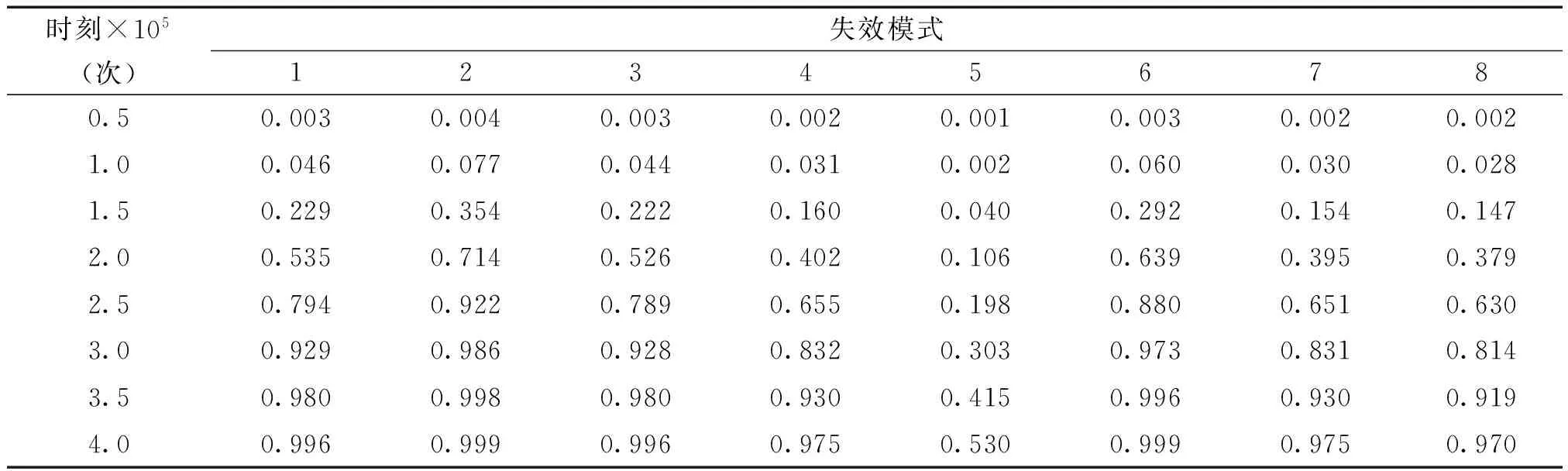
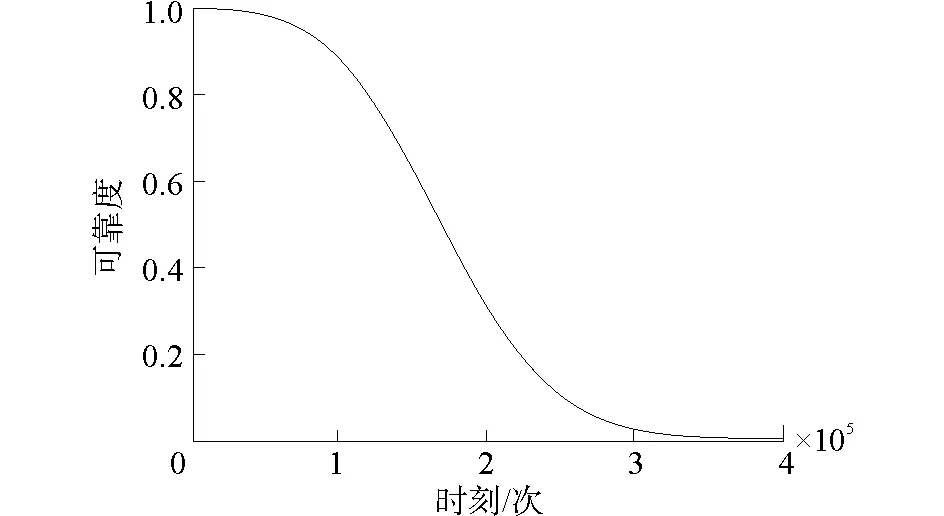
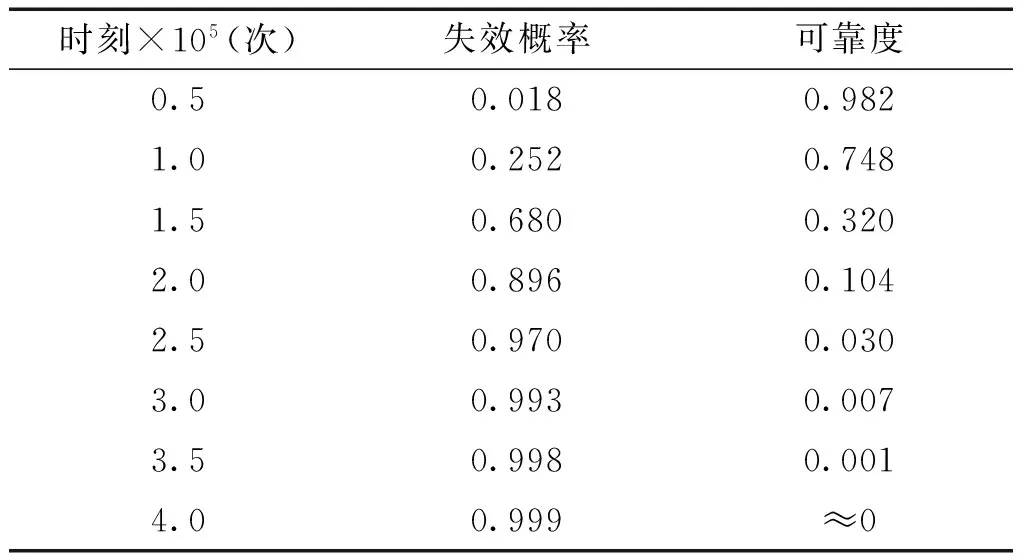
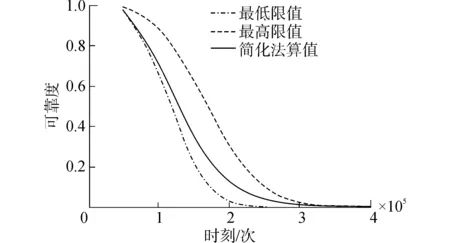
從表7的計算結果可看出，單元為122的n值最小，最小值為488。取nc=1 000，則有n

一個失效模式形成后，檢查該失效模式的最后失效級上是否還有臨界失效元，因為該失效模式的最后失效級是第十五失效級，在第十五失效級上沒有臨界失效元，因此，恢復第十五失效級上的失效元。返回到第十四失效級上，繼續查看是否存在臨界失效元，按此方法進行搜索。由于該失效模式在第十一失效級上存在臨界失效元，所以恢復第十一失效級上的失效元119后，返回到第十失效級上，重新選取臨界失效元120作為第十一失效級上的失效元，將單元120從結構系統中去掉，內力重新分配，按上述方法繼續搜索下一級失效元，直到滿足結構系統失效的條件，又形成了一個新的失效模式，該失效模式的失效路徑如表中的失效模式6所示。

由于該分支的所有失效級上已經沒有臨界失效元，所以該分支的失效模式搜索完畢，然后進行下一新分支的失效模式的搜索。例如以單元119為第一級失效元的新分支，按照上述方法進行新分支的失效模式的搜索。各主要失效模式的失效路徑如表8所示。

表8 失效模式

計算各主要失效模式在各個時刻下的失效概率，計算結果見表9。根據表中的計算結果繪制了失效模式2的可靠度下降曲線，如圖2所示。

同理，其他失效模式也可以繪制出如圖2所示的可靠度下降曲線。從圖中可以看出，該計算結果是令人滿意的，即隨著疲勞載荷循環次數的增加，結構系統的可靠度在不斷減小。

表9 各個失效模式在不同時刻的失效概率

圖2 可靠度下降曲線Fig.2 Decline curve of reliability

各個主要失效模式的失效概率求出后，通過綜合考慮主要失效模式的失效概率來計算實體結構系統的失效概率。首先采用簡單界值法對結構系統的可靠性進行估算。估算結果如表10所示。

表10 疲勞可靠度估算值

采用針對結構系統疲勞可靠性計算的簡化算法計算了結構系統的疲勞可靠度和失效概率，結果列于表11。

同時將表10中的計算結果與表11中的計算結果進行分析并繪制了結構系統的可靠度下降曲線，如圖3所示。

從圖4的計算結果可以看出采用簡化算法計算的結構系統的疲勞可靠度在估算的范圍內，且結構系統的疲勞可靠度的計算結果的趨勢是正確的，即隨著疲勞載荷循環次數的增加，結構系統的可靠度在不斷減小，結構系統的失效概率在不斷增大，該計算結果是符合實際的。

表11結構系統疲勞可靠性的簡化算法計算結果

Table11Resultsoffatiguereliabilityofstructuralsystemonthesimplifiedmethod

時刻×105(次)失效概率可靠度0.50.0180.9821.00.2520.7481.50.6800.3202.00.8960.1042.50.9700.0303.00.9930.0073.50.9980.0014.00.999≈0

圖3 結構系統疲勞可靠度下降曲線Fig.3 Decline curves of fatigue reliability of structural system

4 結論

1) 采用有限體積法分析了實體結構系統的疲勞可靠性。結構系統的疲勞可靠度的計算結果的趨勢是正確的，即隨著疲勞載荷循環次數的增加，結構系統的可靠度在不斷減小。

2)結構系統疲勞可靠性分析大多數以桁架結構為例采用桿單元作為結構元件研究，而文中以實體結構的實體單元作為結構元件研究，給出了實體結構系統疲勞失效的判別準則及搜索結構系統主要失效模式的基本過程，為實體結構系統的疲勞可靠性分析提供了理論參考。

由于采用簡化的疲勞可靠性計算方法計算的結構系統的失效概率，因而沒有充分考慮各失效模式之間的相關性，這點可作為后續工作進行深入研究。

[1] MARTINDALE S G, WIRSCHING P H. Reliability- based progressive fatigue collapse[J].Journal of structural engineering, 1983, 109(8): 1792-1811.

[2] STAHL B, GEYER J F. Fatigue reliability of parallel member systems[J].Journal of structural engineering, 1984, 110(10): 2307-2323.

[3] KARSAN D I, KUMAR A. Fatigue failure paths for offshore platform inspection[J]. Journal of structural engineering, 1990, 116(6): 1679-1695.

[4] SAAD L, AISSANI A, CHATEAUNEUF A, et al. Reliability- based optimization of direct and indirect LCC of RC bridge elements under coupled fatigue- corrosion deterioration processes[J]. Engineering failure analysis, 2016, 59: 570-587.

[5] DI C F, FANELLI P,VIVIO F. Fatigue reliability evaluation of riveted lap joints using a new rivet element and DFR[J]. International journal of fatigue, 2017, 101(2): 192-208.

[6] XU Yazhou. Fatigue reliability evaluation using probability density evolution method[J].Probabilistic engineering mechanics, 2015, 42: 1-6.

[7] YU Feng, GAO Chao, HE Yuting, et al. Investigation on tension- tension fatigue performances and reliability fatigue life of T700/MTM46 composite laminates[J]. Composite structures, 2016, 136: 64-74.

[8] GAO Haifeng, FEI Chengwei, BAI Guangchen, et al. Reliability- based low- cycle fatigue damage analysis for turbine blade with thermo- structural interaction[J]. Aerospace science and technology, 2016, 49: 289-300.

[9] KHASHABA U A, ALJINAIDI A A, HAMED M A. Fatigue and reliability analysis of nano- modified scarf adhesive joints in carbon fiber composites[J]. Composites part b- engineering, 2017, 120: 103-117.

[10] ROVINELLI A,GUILHEM Y, PROUDHON H. Assessing reliability of fatigue indicator parameters for small crack growth via a probabilistic framework[J]. Modelling and simulation in materials science and engineering, 2017, 25(4): 158-170.

[11] MINER M A. Cumulative damage in fatigue[J]. Journal of applied mechanics, 1945, 12(3): 159-164.

[12] 呂海波.結構疲勞可靠性分析方法[D]. 南京:南京航空航天大學， 2000: 28-42. LV Haibo. Study on the method of structural fatigue reliability analysis[D]. Nanjing: Nanjing University of Aeronautics and Astronautics， 2000: 28-42.

Fatiguereliabilityanalysisofstructuralsystembasedonfinitevolumemethod

YU Yanchun1, LI Jiancao2, CHEN Weidong3, LU Shengzhuo3

(1.College of Water Conservancy and Architecture, Northeast Agricultural University, Harbin 150001, China; 2.College of Geographical Information and Tourism, Chuzhou University, Chuzhou 239000, China; 3.College of Astronautics and Architectural Engineering, Harbin Engineering University, Harbin 150001, China)

10.11990/jheu.201605051

http://www.cnki.net/kcms/detail/23.1390.u.201708020.1714.002.html

TB114.3

A

1006- 7043(2017)09- 1413- 07

2016-05-16. < class="emphasis_bold">網絡出版日期

日期：2017-08-20.

國家自然科學基金青年科學基金項目(51508123);安徽省高等學校自然科學研究項目(KJ2015B06);滁州學院科研基金項目(2014QD030，2014PY04).

于艷春(1984-), 女, 講師,博士； 陳衛東(1966-), 男, 教授, 博士生導師； 李建操(1980-), 男, 講師,博士.

李建操,E- mail：lijiancao@yeah.net.

本文引用格式：于艷春，李建操，陳衛東，等. 有限體積法的實體結構疲勞可靠性分析[J]. 哈爾濱工程大學學報， 2017， 38(9): 1413-1419.

YU Yanchun, LI Jiancao, CHEN Weidong, et al. Finite volume analysis of the fatigue reliability of a solid structural system[J]. Journal of Harbin Engineering University， 2017， 38(9): 1413-1419.