改進(jìn)SST湍流模型在分離流中的應(yīng)用

康莊，倪問(wèn)池，孫麗萍

(哈爾濱工程大學(xué) 深海工程技術(shù)中心，黑龍江 哈爾濱 150001)

改進(jìn)SST湍流模型在分離流中的應(yīng)用

康莊，倪問(wèn)池，孫麗萍

(哈爾濱工程大學(xué) 深海工程技術(shù)中心，黑龍江 哈爾濱 150001)

針對(duì)標(biāo)準(zhǔn)SST模型無(wú)法對(duì)分離流動(dòng)進(jìn)行準(zhǔn)確的數(shù)值模擬的問(wèn)題，本文根據(jù)分離流動(dòng)的特性，在傳統(tǒng)SST模型的基礎(chǔ)上增加了能量傳遞耗散項(xiàng)，提升了該模型對(duì)分離流動(dòng)的模擬精度。以開(kāi)源軟件OpenFOAM為平臺(tái)，運(yùn)用改進(jìn)的SST湍流模型，對(duì)亞臨界雷諾數(shù)情況下的圓柱繞流算例進(jìn)行計(jì)算，并結(jié)合已有的實(shí)驗(yàn)結(jié)果，與原始SST模型的計(jì)算結(jié)果進(jìn)行對(duì)比。結(jié)果證明：改進(jìn)的SST模型能有效彌補(bǔ)原始SST模型在模擬分離流時(shí)，漩渦脫落強(qiáng)度偏小的缺陷，對(duì)于亞臨界雷諾數(shù)下的分離流動(dòng)的數(shù)值模擬具有良好效果。

改進(jìn)SST模型； 分離流動(dòng)； 湍流模型； 數(shù)值模擬； 亞臨界雷諾數(shù)； OpenFOAM軟件； 圓柱繞流

Abstract：Given that the standard SST model often fails to produce accurate numerical simulations for separated flow, the simulative precision of the separated flow model can be improved by accounting for the characteristics of separated flow and the increased energy- transfer dissipation item on the basis of the traditional SST model. A flow around a circular cylinder under subcritical Reynolds number was calculated by applying the improved SST turbulence model with the open- source software OpenFOAM as the platform. The calculation results of the original SST model were compared with that of the proposed model. Results showed that the improved SST model can effectively remedy the defect of small- vortex shedding strength in separated flow simulated by the original SST model. Moreover, it has an excellent effect on the numerical simulation of separated flow under subcritical Reynolds number.

Keywords：improved SST model; separated flow; turbulence model; numerical simulation; subcritical Reynolds number; OpenFOAM software; flow around a cylinder

數(shù)值模擬是研究渦分離流動(dòng)重要方法之一。影響數(shù)值模擬結(jié)果的精度的因素很多，其中，湍流模型是影響計(jì)算結(jié)果的重要因素之一[1]。按照不同湍流模型對(duì)N- S方程的求解方法差異，數(shù)值模擬可以分為直接數(shù)值模擬(direct numerical simulation，DNS)、大渦模擬(large eddy simulation，LES)[2]和雷諾平均法模擬(reynolds averaged navier- stokes，RANS)[3]三種方法。DNS與LES法具有較高的計(jì)算精度，但計(jì)算量巨大，計(jì)算時(shí)間過(guò)長(zhǎng)，當(dāng)前難以應(yīng)用于大雷諾數(shù)下復(fù)雜流場(chǎng)的計(jì)算[4]。對(duì)于分離流動(dòng)的數(shù)值模擬，主要還是基于 RANS 方法開(kāi)展。由于分離流動(dòng)流動(dòng)復(fù)雜，常規(guī)的k-ε與k-ω湍流模型，由于存在各自的缺陷，難以獲得精確的計(jì)算結(jié)果[5]。結(jié)合k-ε與k-ω模型優(yōu)勢(shì)的SST模型在當(dāng)前應(yīng)用最廣，然而運(yùn)用原始SST模型計(jì)算分離流動(dòng)，其精度仍然無(wú)法令人滿意。

已有的研究表明，運(yùn)用SST湍流模型對(duì)亞臨界雷諾數(shù)下的圓柱繞流以及圓柱體分離流動(dòng)進(jìn)行數(shù)值模擬，當(dāng)雷諾數(shù)大于104左右時(shí)，分離流動(dòng)的橫向位移以及圓柱繞流的升力系數(shù)的數(shù)值模擬結(jié)果均小于實(shí)驗(yàn)值。運(yùn)用傳統(tǒng)SST模型無(wú)法對(duì)分離流動(dòng)現(xiàn)象進(jìn)行準(zhǔn)確的數(shù)值模擬，必須加以修正。

當(dāng)前，很多學(xué)者對(duì)原始湍流模型進(jìn)行了研究和改進(jìn)[6-11]。任蕓針對(duì)離心泵的特點(diǎn)，利用 RNGk-ε模型和 Realizablek-ε模型對(duì)SST模型進(jìn)行了改進(jìn)，以考慮大旋轉(zhuǎn)和曲率影響[12]。甘文彪對(duì)原始SST模型進(jìn)行了分離修正與可壓性修正，提高了模型預(yù)測(cè)分離流動(dòng)的能力[13]。Zhang等對(duì)SST模型進(jìn)行改進(jìn)，用以計(jì)算海洋表面溫度[14]。這些改進(jìn)針對(duì)各自的問(wèn)題取得了較好的效果，但無(wú)法直接應(yīng)用于分離流動(dòng)的模擬。

本文基于SST模型的上述缺陷，根據(jù)分離流動(dòng)的特性，在傳統(tǒng)SST模型的基礎(chǔ)上增加了能量傳遞項(xiàng)，提升了該模型對(duì)分離流動(dòng)的模擬精度，并以開(kāi)源軟件OpenFOAM為平臺(tái)，運(yùn)用改進(jìn)的SST湍流模型，對(duì)典型雷諾數(shù)下的圓柱繞流算例進(jìn)行計(jì)算，驗(yàn)證其性能。

1 SST湍流模型

1.1 原始SST模型

剪應(yīng)力輸運(yùn)(shear stress transport，SST) 模型是由Menter于1994年提出的，其基本思路是通過(guò)變形，將k-ε湍流模型與Wilcox 兩方程k-ω湍流模型通過(guò)混合函數(shù)結(jié)合起來(lái)[15]。在近壁面使用k-ω模型，在遠(yuǎn)離壁面充分發(fā)展的流場(chǎng)中采用k-ε湍流模型，充分結(jié)合了k-ω模型對(duì)分離流模擬精度高以及k-ε模型對(duì)湍流初始參數(shù)敏感度低的優(yōu)勢(shì)，是當(dāng)前應(yīng)用最廣的湍流模型之一，其無(wú)量綱的形式如下

渦粘性

(1)

湍動(dòng)能

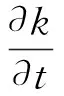
(2)

比耗散率

(3)

其中,第二混合函數(shù)

(4)

湍動(dòng)能k的生成項(xiàng)

(5)

第一混合函數(shù)

(6)

式中：

(7)

F1在近壁面處取1，在遠(yuǎn)離近壁面處取值為0，從而實(shí)現(xiàn)k-ε與k-ω模型的切換。相應(yīng)地，輸運(yùn)方程中的各系數(shù)也可由混合函數(shù)F1表示。

φ=φ1F1+φ2(1-F1)

(8)

1.2 改進(jìn)SST模型

已有的研究成果表明，傳統(tǒng)的k-ε以及SST模型在模擬分離流動(dòng)時(shí)，無(wú)法獲得令人滿意的結(jié)果，計(jì)算所得的漩渦脫落強(qiáng)度明顯小于實(shí)驗(yàn)觀測(cè)值[16-17]。Medic認(rèn)為，標(biāo)準(zhǔn)雷諾平均湍流模型的耗散率方程在預(yù)測(cè)分離流動(dòng)時(shí)存在缺陷，將會(huì)產(chǎn)生較大的計(jì)算誤差以至于抑制渦的脫落[18]。在標(biāo)準(zhǔn)雷諾平均湍流模式建立中，渦一般被定義為兩種尺度，一種是與時(shí)均流動(dòng)發(fā)生相互作用的大尺度渦結(jié)構(gòu)(large eddies)，這類渦通過(guò)與時(shí)均剪切運(yùn)動(dòng)的作用，從時(shí)均流動(dòng)能中源源不斷地提取能量以維持湍流的脈動(dòng)運(yùn)動(dòng)。另一種尺度的渦是耗散渦結(jié)構(gòu)(dissipative eddies)，這類渦尺度很小，它們通過(guò)粘性起耗散湍流脈動(dòng)動(dòng)能的作用[19]。對(duì)此，Younis經(jīng)過(guò)大量的理論與實(shí)驗(yàn)分析，認(rèn)為渦在從大尺度變?yōu)樾〕叨鹊倪^(guò)程中，也存在能量耗散，且耗散頻率與渦泄頻率相同[20]。因此，當(dāng)漩渦產(chǎn)生時(shí)，耗散譜應(yīng)當(dāng)變?yōu)橐韵滦问剑?/p>

e(κ,t)=(A0+A(t))κs

(9)

式中：A0是常數(shù)，κ為波數(shù)，s為待定系數(shù)，A(t)是反應(yīng)渦從大尺度變?yōu)樾〕叨鹊倪^(guò)程中，存在的能量耗散的附加項(xiàng)，它在平穩(wěn)流動(dòng)中應(yīng)當(dāng)趨于0。

根據(jù)湍動(dòng)能k與耗散譜的關(guān)系

(10)

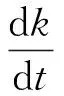
(11)

可以推出分離流動(dòng)中，耗散率ε的表達(dá)式應(yīng)當(dāng)為

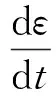
(12)

根據(jù)上述ε的表達(dá)式，并通過(guò)定義A(t)的表達(dá)形式，Younis針對(duì)k-ε模型，建議對(duì)耗散率方程中的系數(shù)Cε1進(jìn)行如下修正(k-ε模型的具體形式見(jiàn)文獻(xiàn)[21])：

(13)

上述湍流模型對(duì)分離流動(dòng)的計(jì)算精度雖有提高，但此模型的穩(wěn)定性較差，特別對(duì)于雷諾數(shù)較低的情況，有較大的誤差。可將此修正思路應(yīng)用于SST模型，從而提高該模型對(duì)逆壓梯度的靈敏度，降低近壁區(qū)的計(jì)算難度，從而實(shí)現(xiàn)對(duì)分離流動(dòng)更準(zhǔn)確的預(yù)報(bào)。

本文借鑒Younis針對(duì)k-ε模型耗散率方程的修正思路，根據(jù)ε和ω的關(guān)系式ε=Cμkω，將k-ε模型耗散率方程的修正項(xiàng)轉(zhuǎn)化為用ω表示的比耗散率的形式，并根據(jù)SST模型比耗散率方程的形式進(jìn)行相應(yīng)變換，得到新的修正項(xiàng)形式為

(14)

式中：Q為時(shí)均流場(chǎng)中每個(gè)單位體積中的湍動(dòng)能，k為湍動(dòng)能，Pk為湍動(dòng)能k的生成項(xiàng)，β′為經(jīng)驗(yàn)常數(shù)，根據(jù)數(shù)值優(yōu)化方法[22]求得。本文經(jīng)過(guò)反復(fù)調(diào)試，取β′=0.54。將R項(xiàng)添加到原始SST方程的比耗散率輸運(yùn)方程中，得到改進(jìn)的SST比耗散率方程形式如下：

(15)

其余的方程與系數(shù)均與原始SST模型相同，得到改進(jìn)SST湍流模型。

2 圓柱繞流數(shù)值模型

2.1 計(jì)算域及網(wǎng)格

本文在亞臨界雷諾數(shù)下，分別用原始以及改進(jìn)的SST湍流模型進(jìn)行圓柱繞流數(shù)值模擬，并對(duì)模擬結(jié)果進(jìn)行詳細(xì)的對(duì)比分析。

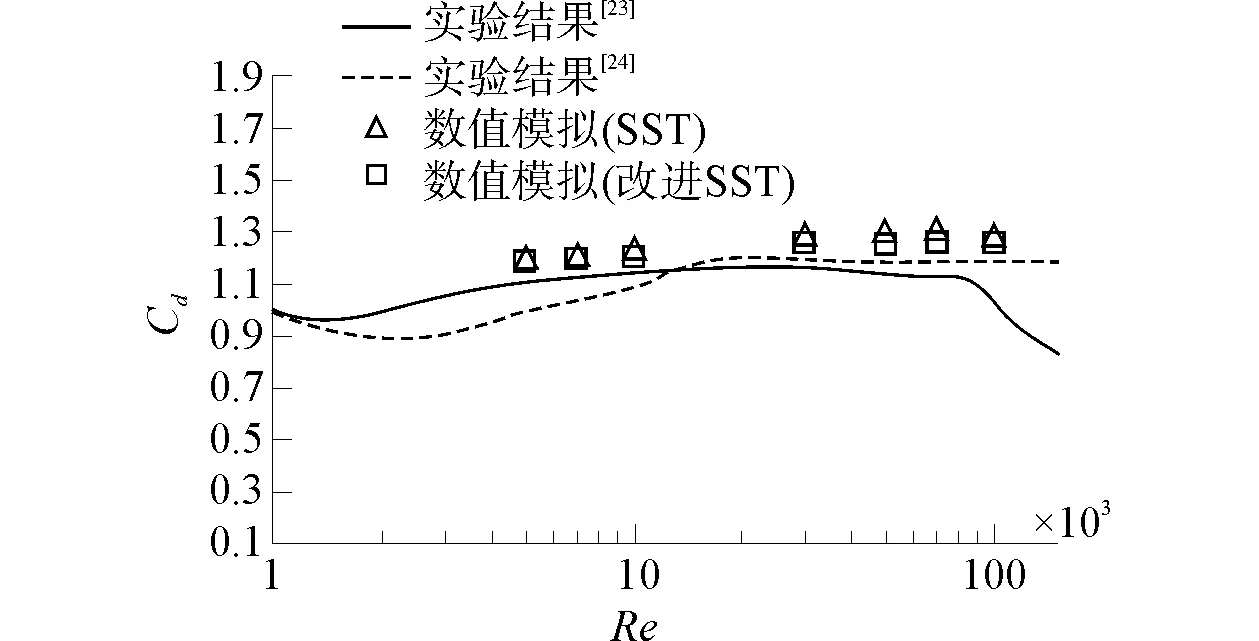
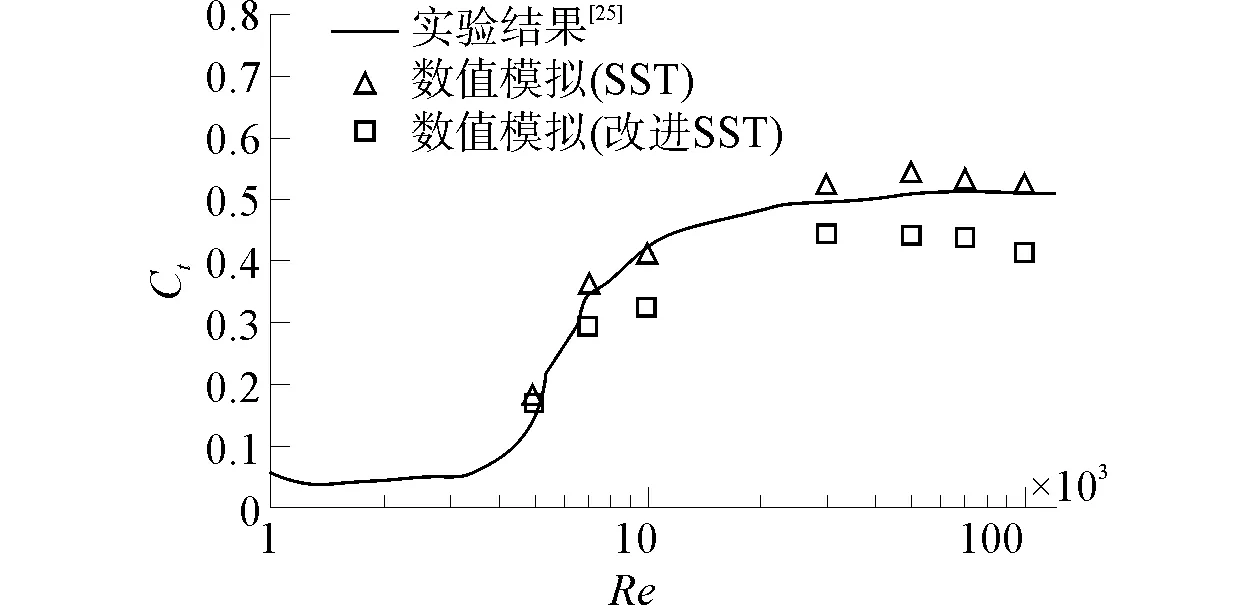
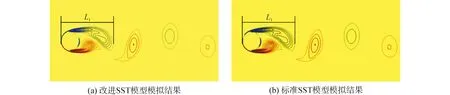
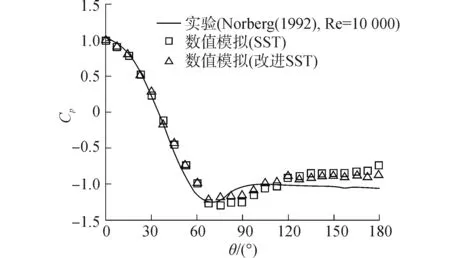
本次模擬所使用的網(wǎng)格如圖1、圖2所示。其中，坐標(biāo)系定義為：以圓柱中心點(diǎn)為坐標(biāo)原點(diǎn)，來(lái)流方向?yàn)閤軸方向，垂直來(lái)流方向?yàn)閥軸方向，z軸方向?yàn)閳A柱展向。計(jì)算域劃分為：-6D

圖1 計(jì)算域整體網(wǎng)格Fig.1 Global mesh for circular cylinder

圖2 圓柱周圍局部網(wǎng)格Fig.2 Local mesh for circular cylinder

網(wǎng)格劃分為：圓柱周圍3D的范圍內(nèi)采用O型網(wǎng)格，在其他區(qū)域使用六面體網(wǎng)格。網(wǎng)格數(shù)量根據(jù)雷諾數(shù)不同進(jìn)行相應(yīng)的調(diào)整，改變貼近圓柱表面的第一層網(wǎng)格厚度，保證y+<1。邊界條件為：圓柱表面采用無(wú)滑移固壁，入口采用均勻來(lái)流，出口采用壓力梯度為零，其余均為對(duì)稱邊界。

2.2 計(jì)算方法

對(duì)SST湍流模型的改進(jìn)通過(guò)開(kāi)源軟件OpenFOAM實(shí)現(xiàn)。計(jì)算過(guò)程中，各項(xiàng)的離散方法如下：時(shí)間項(xiàng)采用 backward 隱式歐拉格式進(jìn)行離散，對(duì)流項(xiàng)采用帶限制器的線性差分(total variation diminishing, TVD)格式進(jìn)行離散，擴(kuò)散項(xiàng)采用高斯線性守恒格式進(jìn)行離散。

3 數(shù)值模擬結(jié)果分析

3.1 基本參數(shù)分析

本文選取圓柱繞流穩(wěn)定階段的數(shù)據(jù)，對(duì)其進(jìn)行相應(yīng)的后處理，得到各工況下，圓柱繞流的平均阻力系數(shù)、均方根升力系數(shù)以及ST數(shù)等基本參數(shù)，如表1所示。

為了驗(yàn)證本文改進(jìn)湍流模型的性能，分別將兩種湍流模型的阻力系數(shù)、ST數(shù)數(shù)值模擬結(jié)果與文獻(xiàn)[23-24]實(shí)驗(yàn)觀測(cè)結(jié)果進(jìn)行對(duì)比，并將數(shù)值模擬結(jié)果與對(duì)應(yīng)的實(shí)驗(yàn)觀測(cè)結(jié)果繪在同一圖中，如圖3、圖4所示。

表1 圓柱繞流基本參數(shù)數(shù)值模擬結(jié)果

圖3 平均阻力系數(shù)對(duì)比圖Fig.3 Contrast of average drag coefficient

圖4 ST數(shù)對(duì)比圖Fig.4 Contrast of ST number

從圖3與圖4中可以看出，改進(jìn)SST模型的平均阻力系數(shù)計(jì)算結(jié)果較原始SST模型略微偏大，但差異很小，可以忽略。對(duì)于ST數(shù)，改進(jìn)SST模型的計(jì)算結(jié)與原始SST模型的計(jì)算結(jié)果完全一致。根據(jù)本文的理論，改進(jìn)模型中所添加的能量耗散項(xiàng)的能量耗散頻率等于渦泄頻率，因此添加的R項(xiàng)不會(huì)改變圓柱繞流的漩渦脫落頻率，因此ST數(shù)不會(huì)改變。該數(shù)值模擬的結(jié)果與理論吻合。總而言之，對(duì)于分離流動(dòng)的平均阻力系數(shù)以及ST數(shù)，運(yùn)用改進(jìn)SST湍流模型的計(jì)算結(jié)果與原始SST模型的計(jì)算結(jié)果差異較小，且與實(shí)驗(yàn)值吻合度較好。

圖5為兩種湍流模型的均方根升力系數(shù)數(shù)值模擬結(jié)果與文獻(xiàn)[25]實(shí)驗(yàn)觀測(cè)結(jié)果對(duì)比圖。從圖5中可以看出，當(dāng)雷諾數(shù)較小時(shí)，兩種湍流模型的升力系數(shù)計(jì)算結(jié)果相近，且與實(shí)驗(yàn)值吻合較好，但當(dāng)雷諾數(shù)較大時(shí)，運(yùn)用原始SST模型計(jì)算所得的圓柱繞流均方根升力系數(shù)始終小于實(shí)驗(yàn)觀測(cè)值，偏差較大，可見(jiàn)在較大雷諾數(shù)情況下原始SST模型會(huì)產(chǎn)生較大的誤差，抑制渦的脫落，從而使得升力系數(shù)明顯偏小。此時(shí)，改進(jìn)SST模型的升力系數(shù)計(jì)算結(jié)果較原始SST模型的結(jié)果顯著增大，并且與實(shí)驗(yàn)觀測(cè)值的誤差較小。因此，本文改進(jìn)的SST模型能有效克服標(biāo)準(zhǔn)模型抑制渦脫落的缺陷，顯著提升分離流動(dòng)升力系數(shù)的數(shù)值模擬精度。

圖5 均方根升力系數(shù)對(duì)比圖Fig.5 Contrast of RMS lift coefficient

3.2 尾渦與流場(chǎng)分析

圖6與圖7分別為Re=5 000 與Re=100 000 時(shí)圓柱繞流的等值線渦量圖，其中，L1表示尾流區(qū)的回流區(qū)長(zhǎng)度。從圖中可以看出，兩種湍流模型都能捕捉到明顯的“2S模式”尾渦[26]，并且在雷諾數(shù)較低時(shí)，尾渦的形態(tài)區(qū)別不大。然而當(dāng)雷諾數(shù)較大時(shí)，改進(jìn)SST模型模擬的尾流區(qū)的回流區(qū)長(zhǎng)度明顯大于標(biāo)準(zhǔn)SST模型的模擬結(jié)果。結(jié)合圖5升力系數(shù)的模擬結(jié)果可知，標(biāo)準(zhǔn)SST湍流模型在模擬較高雷諾數(shù)的分離流動(dòng)時(shí)，回流區(qū)長(zhǎng)度不足，渦脫落受到抑制，使得升力系數(shù)的計(jì)算結(jié)果明顯偏小。進(jìn)一步驗(yàn)證了改進(jìn)SST湍流模型能有效克服標(biāo)準(zhǔn)SST模型在雷諾數(shù)較大時(shí)，預(yù)測(cè)分離流動(dòng)漩渦脫落強(qiáng)度不足的缺陷，大大提升了分離流的模擬精度。

圖6 兩種湍流模型渦量圖Re=5 000Fig.6 Vorticity contours with two turbulence models when Re=5 000

圖8為Re=10 000的情況下，沿圓柱表面周向的時(shí)均壓力系數(shù)分布圖。沿圓周方向均勻取48個(gè)點(diǎn)，記錄各點(diǎn)的平均壓力數(shù)據(jù)，以表示圓柱表面壓力系數(shù)分布。圖中可以看出，改進(jìn)SST模型周向壓力響應(yīng)的最小值點(diǎn)約為65°處，且壓力系數(shù)約為-1.2左右，與實(shí)驗(yàn)值基本吻合，而標(biāo)準(zhǔn)SST模型周向壓力響應(yīng)的最小值點(diǎn)約為70°處，且壓力系數(shù)約為-1.3左右，其位置和大小相較于實(shí)驗(yàn)結(jié)果均有相對(duì)較大的偏差。可見(jiàn)改進(jìn)SST模型對(duì)于流場(chǎng)的壓力分布具有更高的模擬精度。

圖7 兩種湍流模型渦量圖Re=100 000Fig.7 Vorticity contours with two turbulence models when Re=100 000

圖8 沿圓柱表面周向的時(shí)均壓力系數(shù)分布圖Fig.8 Pressure coefficient distribution around cylinder surface

4 結(jié)論

1)改進(jìn)SST湍流模型對(duì)分離流動(dòng)均方根升力系數(shù)模擬結(jié)果的準(zhǔn)確性較原始SST模型有顯著提升。

2)當(dāng)雷諾數(shù)較大時(shí)，改進(jìn)SST模型模擬的尾流區(qū)的回流區(qū)長(zhǎng)度明顯大于標(biāo)準(zhǔn)SST模型的模擬結(jié)果。

3)改進(jìn)SST模型對(duì)于流場(chǎng)的壓力分布具有更高的模擬精度。

4)本文所改進(jìn)的SST湍流模型能有效彌補(bǔ)原始SST模型在模擬較高雷諾數(shù)下的分離流動(dòng)時(shí)，漩渦脫落強(qiáng)度偏小的缺陷，對(duì)于亞臨界雷諾數(shù)下的分離流動(dòng)的數(shù)值模擬具有良好效果。

[1] YANG Xiaoyu, TUCKER P G. Assessment of turbulence model performance: Severe acceleration with large integral length scales [J]. Computers & fluids, 2016, 126: 181-191.

[2] BASSI F, BOTTI L, COLOMBO A, et al. On the development of an implicit high- order discontinuous galerkin method for DNS and implicit LES of turbulent flows [J]. European journal of mechanics - b/fluids, 2015, 51(13): 1758-1760.

[3] ASHTON N, WEST A, LARDEAU S, et al. Assessment of RANS and DES methods for realistic automotive models [J]. Computers & fluids, 2016, 128: 1-15.

[4] SPALART P R. Strategies for turbulence modelling and simulations [J]. International journal of heat & fluid flow, 2000, 21(3): 252-263.

[5] JOHANSSON S H, DAVIDSON L, OLSSON E. Numerical simulation of vortex shedding past triangular cylinders at high Reynolds number using a k- ε turbulence model [J]. International journal for numerical methods in fluids, 1993, 16(10): 859-878.

[6] 顧璇, 郜冶, 賀征,等. 小離地高度下翼型氣動(dòng)特性計(jì)算模型的研究[J]. 哈爾濱工程大學(xué)學(xué)報(bào), 2008, 29(11): 1160-1165. GU Xuan, GAO Ye, HE Zheng, et al. Modeling aerodynamic performance of an airfoil with small ground clearance[J]. Journal of Harbin Engineering University, 2008, 29(11): 1160-1165.

[7] MA Y, ZHOU X, BI D, et al. Improved air- sea flux algorithms in an ocean- atmosphere coupled model for simulation of global ocean SST and its tropical pacific variability [J]. Climate dynamics, 2015, 44 (5-6): 1473-1485.

[8] ROCHA P A C, ROCHA H H B, CARNEIRO F O M, et al.k-ωSST (shear stress transport) turbulence model calibration: A case study on a small scale horizontal axis wind turbine [J]. Energy, 2013, 65(C): 412-418.

[9] KIM Y, XIE Z T. Modelling the effect of freestream turbulence on dynamic stall of wind turbine blades [J]. Computers & fluids, 2016, 129: 53-66.

[10] BALOGH M, PARENTE A. Realistic boundary conditions for the simulation of atmospheric boundary layer flows using an improvedk-εmodel [J]. Journal of wind engineering & industrial aerodynamics, 2015, 144: 183-190.

[11] 陳慶光, 徐忠, 張永建. RNGk-ε模式在工程湍流數(shù)值計(jì)算中的應(yīng)用[J]. 力學(xué)季刊, 2003, 24(1):88-95. CHENG Qingguang, XU Zhong, ZHANG Yongjian. Application of RNGk-εmodels in numerical simulations of engineering turbulent flows [J]. Chinese quarterly of mechanics, 2003.

[12] 任蕓, 劉厚林, 舒敏驊,等. 考慮旋轉(zhuǎn)和曲率影響的SSTk-ω湍流模型改進(jìn)[J]. 農(nóng)業(yè)機(jī)械學(xué)報(bào), 2012, 43(11): 123-128. REN Yun, LIU Houlin, SHU Minhua, et al. Improvement of SSTk-ωturbulence model and numerical simulation in centrifugal pump [J]. Transactions of the Chinese society for agricultural machinery, 2012， 43(11): 123-128.

[13] 甘文彪, 周洲, 許曉平,等. 基于改進(jìn)SST模型的分離流動(dòng)數(shù)值模擬[J]. 推進(jìn)技術(shù), 2013, 34(5): 595-602. GAN Wenbiao, ZHOU Zhou, XU Xiaoping, et al. Investigation on improving the capability of predicting separation in modified SST turbulence model [J]. Tuijin jishu/journal of propulsion technology, 2013, 34(5): 595-602.

[14] ZHANG R H, KLEEMAN R, ZEBIAK S E, et al. An empirical parameterization of subsurface entrainment temperature for improved SST anomaly simulations in an intermediate ocean model [J]. Journal of climate, 2005, 18(2): 350-371.

[15] MENTER F R. Two- equation eddy- viscosity turbulence models for engineering applications [J]. Aiaa journal, 2012, 32(8): 1598-1605.

[17] JUNG Y W, PARK S O. Vortex- shedding characteristics in the wake of an oscillating airfoil at low Reynolds number [J]. Journal of fluids & structures, 2005, 20(3): 451-464.

[18] MEDIC G. Etude mathématique des modèles aux tensions de reynolds et simulation numérique d′écoulements turbulents sur parois fixes et mobiles[J]. Bibliogr, 1999.

[19] 張兆順. 湍流理論與模擬[M]. 北京：清華大學(xué)出版社, 2005. ZHANG Zhaoshun. Theory and modeling of turbulence[M]. Beijing: Tsinghua University Press, 2005.

[20] YOUNIS B A, PRZULJ V P. Computation of turbulent vortex shedding [J]. Computational mechanics, 2006, 37(5): 408-425.

[21] WILCOX D C. Turbulence modeling for CFD [J]. Dcw industries la Canada California USA, 1998: 363-367.

[22] SU J, GU Z, XU X. Advances in numerical methods for the solution of population balance equations for disperse phase systems [J]. Science in China, 2009, 52(8): 1063-1079.

[23] ZDRAVKOVICH M M. Conceptual overview of laminar and turbulent flows past smooth and rough circular cylinders [J]. Journal of wind engineering & industrial aerodynamics, 1990, 33(1): 53-62.

[24] ESD U. Mean forces, pressure and flow field velocities for circular cylindrical structures single cylinder with two- dimensional flow: 80025 [S]. UK, London: IHS ESDU International Plc, 1986: 1-66.

[25] NORBERG C. Fluctuating lift on a circular cylinder: review and new measurements [J]. Journal of fluids & structures, 2003, 17(1): 57-96.

[26] KANG Z, NI W, SUN L. An experimental investigation of two- degrees- of- freedom VIV trajectories of a cylinder at different scales and natural frequency ratios[J]. Ocean engineering, 2016, 126: 187-202.

ApplicationoftheimprovedSSTturbulencemodelforseparatedflow

KANG Zhuang, NI Wenchi, SUN Liping

(Deepwater Engineering Research Center, Harbin Engineering University, Harbin 150001, China)

10.11990/jheu.201606063

http://www.cnki.net/kcms/detail/23.1390.u.20170426.1801.070.html

U661.1

A

1006- 7043(2017)09- 1359- 06

2016-06-22. < class="emphasis_bold">網(wǎng)絡(luò)出版日期

日期：2017-04-26.

國(guó)家青年自然科學(xué)基金項(xiàng)目(51509045);國(guó)家留學(xué)基金項(xiàng)目(201606680106); 中央高校基本科研業(yè)務(wù)費(fèi)專項(xiàng)資金—博士研究生科研創(chuàng)新基金項(xiàng)目(HEUGIP201702).

康莊(1978-),男,副教授,博士生導(dǎo)師； 倪問(wèn)池(1991-),男,博士研究生.

倪問(wèn)池, E- mail：niwenchi@hrbeu.edu.cn.

本文引用格式：康莊，倪問(wèn)池，孫麗萍. 改進(jìn)SST湍流模型在分離流中的應(yīng)用[J]. 哈爾濱工程大學(xué)學(xué)報(bào)， 2017， 38(9): 1359-1364.

KANG Zhuang, NI Wenchi, SUN Liping. Application of the improved SST turbulence model for separated flow[J]. Journal of Harbin Engineering University， 2017， 38(9): 1359-1364.