一種特殊的多米諾擴縮運算

劉小青 許 進

?

一種特殊的多米諾擴縮運算

劉小青 許 進*

(北京大學(xué)信息科學(xué)技術(shù)學(xué)院 北京 100871);(北京大學(xué)高可信軟件技術(shù)教育部重點實驗室 北京 100871)

該文提出一種稱為334擴縮運算的多米諾擴縮運算。使用該運算構(gòu)造了一類特殊的極大平面圖——334-型極大平面圖，證明了該類圖均為樹型2-色不變?nèi)χ颐總€-階334-型極大平面圖恰有個2-色不變?nèi)χ皞€樹著色。證明了該運算可用于構(gòu)造純樹著色極大平面圖，并提出猜想：若極大平面圖是純樹(純?nèi)Γ旌?著色，則對實施334擴(縮)輪運算后，所得之圖仍是純樹(純?nèi)Γ旌?著色。

半封漏斗；樹型2-色不變?nèi)χ患儤渲?34擴輪運算

1 引言

文獻[6,7]對平面圖的著色類型進行了研究，將著色分為樹著色和圈著色，依據(jù)著色類型將4-色平面圖分為3類：純樹著色型、純?nèi)χ秃突旌现停⑻岢隽思儤渲孪搿耙粋€平面圖是純樹著色圖當(dāng)且僅當(dāng)它是正二十面體或啞鈴極大平面圖”，若該猜想成立，則著名的已有43年歷史的唯一4-色平面圖猜想成立。文獻[13]定義了一類特殊的圈著色2-色不變?nèi)χ诖嘶A(chǔ)上，將4-色非Kempe平面圖的Kempe等價類分為樹型，圈型和循環(huán)圈型，這也是非Kempe平面圖存在的根源。若一個-色圖的都有-著色構(gòu)成一個Kempe等價類，則稱該圖為Kempe圖。

本文給出了一種構(gòu)造具有相同著色類型的極大平面圖類的方法，包含334擴輪運算和334縮輪運算。具體安排如下：第2節(jié)給出了334擴輪運算及334縮輪運算的定義；第3節(jié)基于334擴縮運算研究了一類樹型2-色不變?nèi)χ珮O大平面圖334-型極大平面圖的基本性質(zhì)；第4節(jié)討論了334-型極大平面圖的著色性質(zhì)；第5節(jié)給出了用334擴輪運算構(gòu)造純樹著色極大平面圖的方法。

文中未給出的相關(guān)定義、記號與理論參見文獻[6,13-15]。

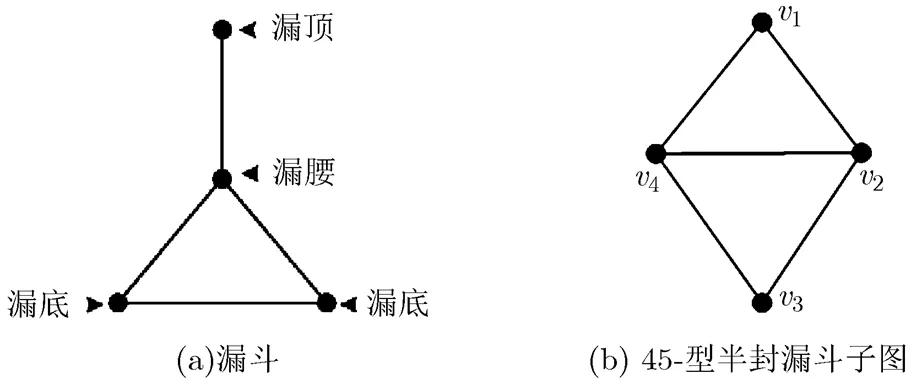
圖1 漏斗與45-型半封漏斗子圖

2 334擴縮運算

把圖1(a)中所示的圖稱為漏斗，其中度數(shù)為1的頂點稱為漏頂；度數(shù)為3的頂點稱為漏腰；2個度數(shù)為2的頂點稱為漏底。若一個圖的頂點導(dǎo)出子圖是漏斗，則該子圖稱為漏斗子圖。334擴縮運算本質(zhì)上是一種多米諾擴縮運算[14]，其中，334擴輪運算包含2次擴3-輪運算以及一次擴4-輪運算；334縮輪運算包含2次縮3-輪運算以及一次縮4-輪運算。設(shè)是一個極大平面圖，圖是一個標(biāo)號如圖1(b)所示的半封漏斗。若是的一個子圖，且，，則稱是的一個45-型半封漏斗子圖，簡稱為45-型子圖。

334擴輪運算的對象圖是極大平面圖中的45-型子圖。334擴輪運算，記作，是指按照如下步驟，將的一個45-型子圖(如圖1(b)所示)變成圖2(a)~2(d)中最右邊所示構(gòu)形的過程：

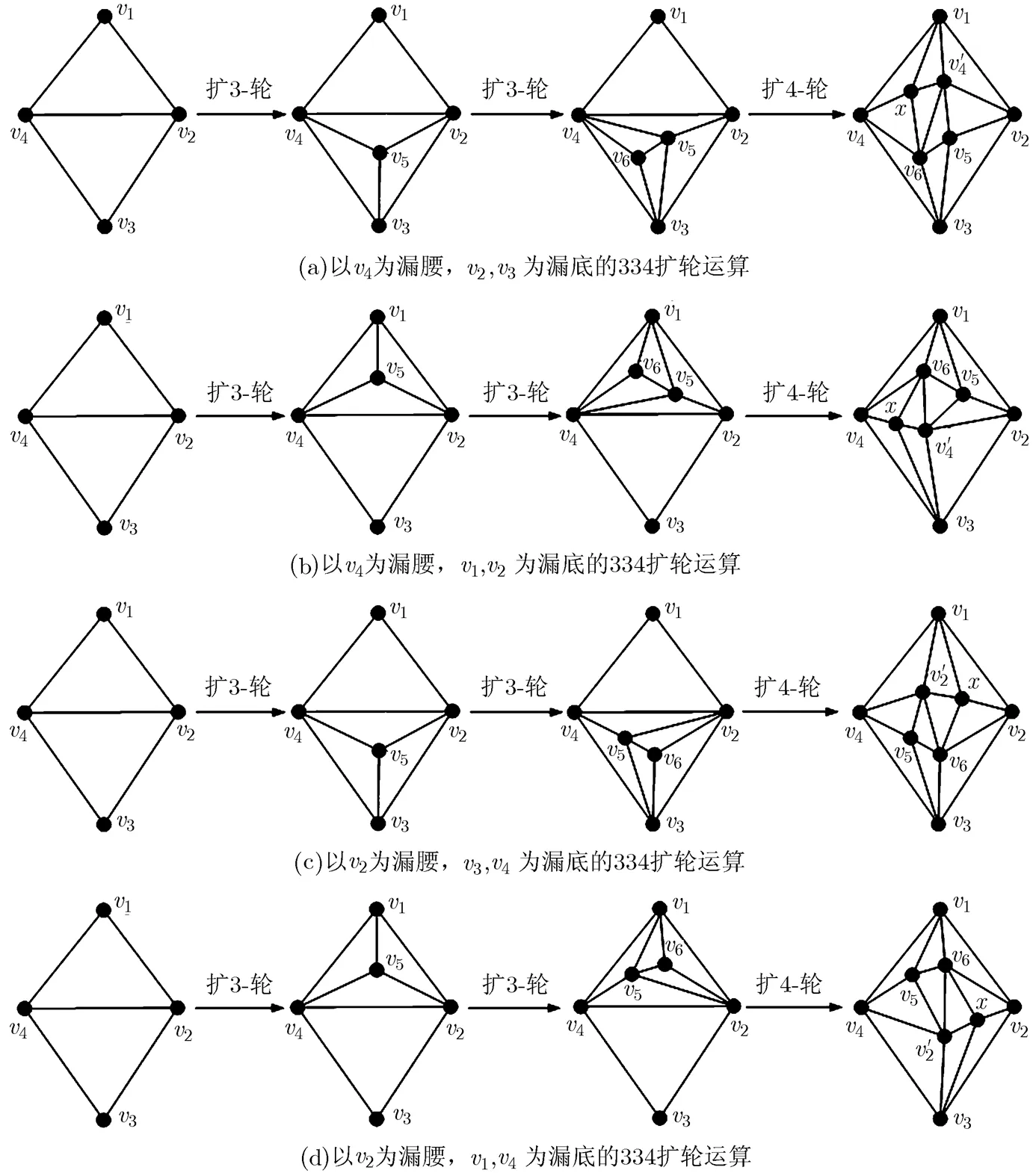
圖2 選擇不同漏腰和漏底的334擴輪運算過程示意圖

(2)在圖2(a)與圖2(d)中，2個最右邊構(gòu)形的區(qū)別僅是構(gòu)形的內(nèi)部頂點標(biāo)號不同，若對一個極大平面圖的同一個45-型子圖分別實施如圖2(a)和圖2(d)所示過程的334擴輪運算，則得到2個相同的極大平面圖，故視這2個構(gòu)形是相同的；同理，圖2(b)與圖2(c)中2個最右邊的構(gòu)形是相同的。

圖3(a)，圖3(d)，圖3(e)，圖3(h)中最右邊構(gòu)形的區(qū)別僅是構(gòu)形的頂點標(biāo)號方式不同，對一個極大平面圖的同一個334子圖分別實施如圖3(a)，圖3(d)，圖3(e)，圖3(h)所示過程的334縮輪運算，則得到4個相同的極大平面圖，故視圖3(a)，圖3(d)，圖3(e)，圖3(h)中最右邊的構(gòu)形是相同的；同理，圖3(b)，圖 3(c)，圖3(f)，圖3(g)中最右邊的構(gòu)形是相同的。

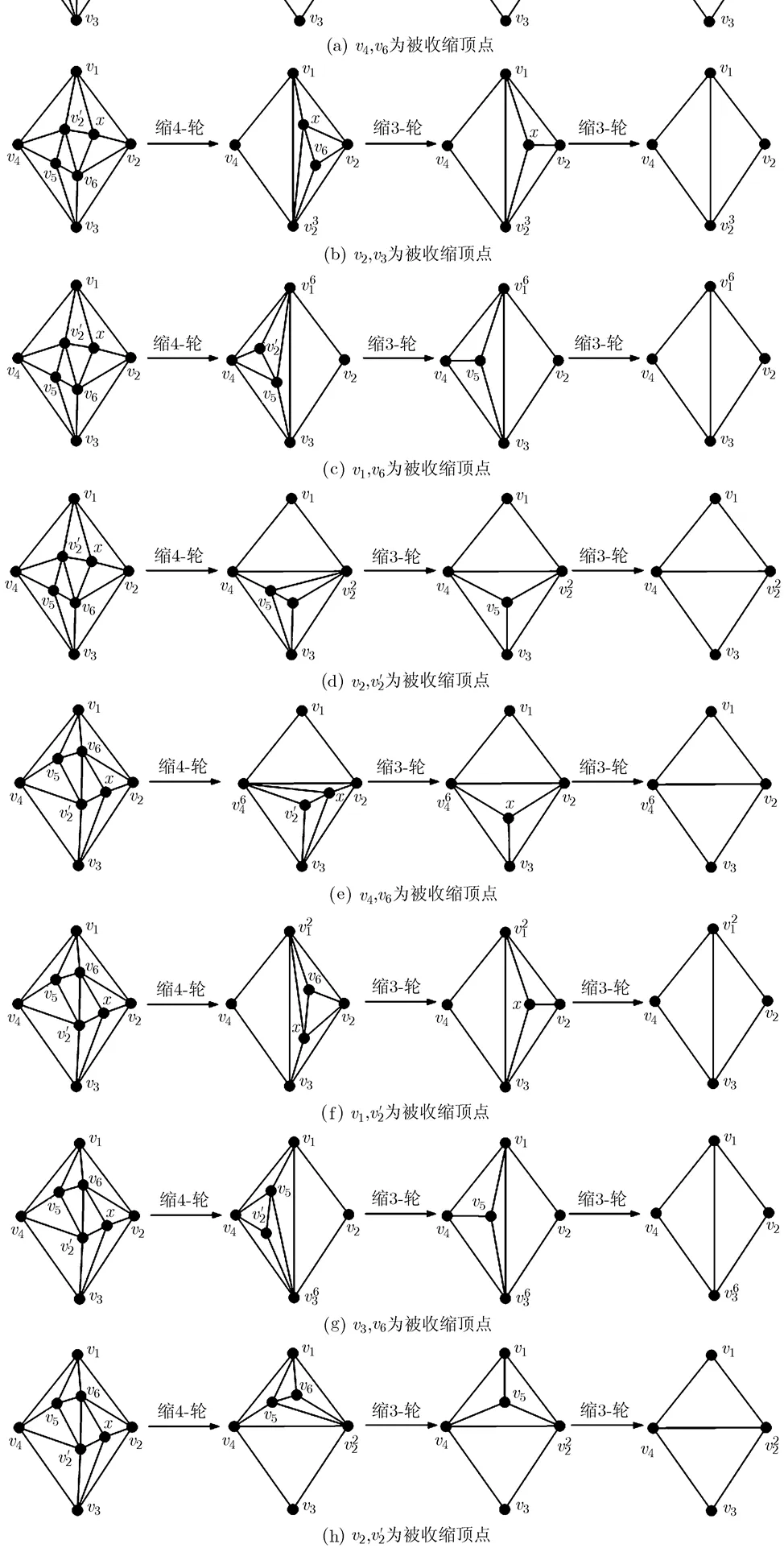
圖3 選擇不同被收縮點對的334縮輪運算過程示意圖

3 334-型極大平面圖

3.1334-型極大平面圖及構(gòu)造

圖4所示的圖是階數(shù)最小的最小度為4且含45-型子圖的極大平面圖，稱為8-階334-型極大平面圖，記作。

3.2 334-型極大平面圖的基本性質(zhì)

由定理2可推出下述結(jié)論：

證明 由前面討論知，任意334子圖僅有一個與之不相同的334子圖。

圖4 8-階334-型極大平面圖 圖5 2個12-階334-型極大平面圖

若將圖5(a)中上方的334子圖替換為與之不相同的334子圖，如圖6(a)所示，則得到一個與圖5(b)同構(gòu)的圖；若將圖5(a)中下方的334子圖替換為與之不相同的334子圖，如圖6(b)所示，則得到一個與圖5(b)同構(gòu)的圖。若將圖5(b)中的任意一個334子圖替換為與之不相同的334子圖，則得到與圖5(a)同構(gòu)的圖。故時結(jié)論成立。

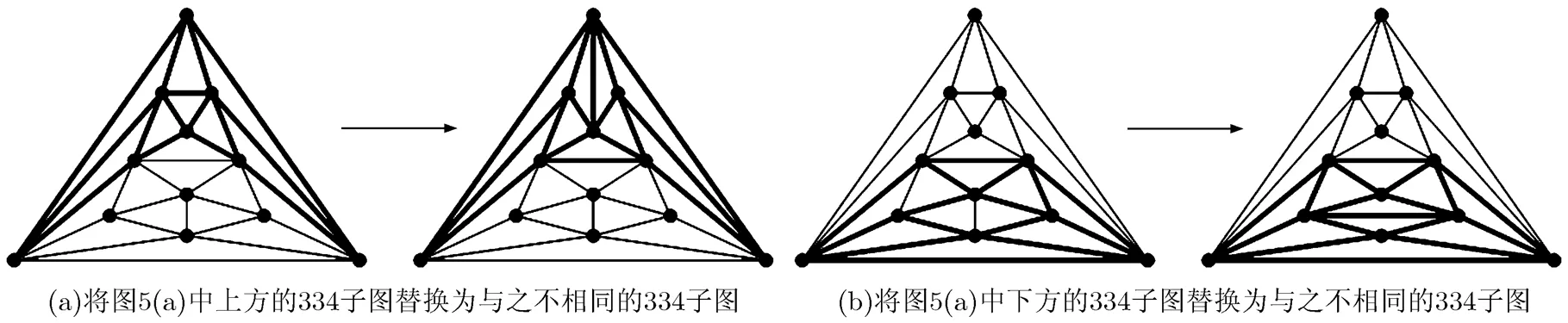
圖6 定理3證明示意圖

由推論1和定理3，可直接推出下述結(jié)論：

定理4 每個334-型極大平面圖恰有4個4度頂點。

8-階334-型極大平面圖為如圖4所示的圖，其度序列為44445555，結(jié)論成立。12-階334-型極大平面圖共有2個，分別如圖5(a)，圖5(b)所示，它們均恰含4個4度頂點，結(jié)論成立。

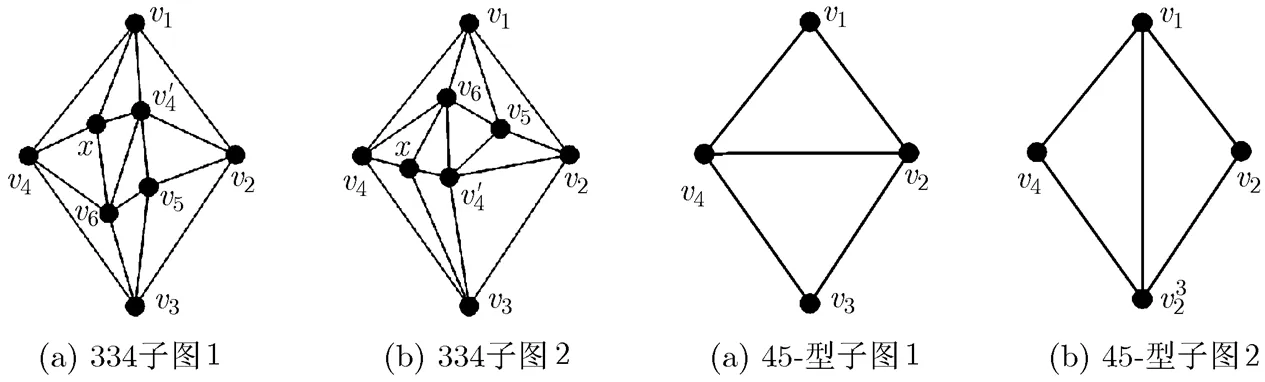
圖7 2個不相同的334子圖　　　　　　圖8 2個不相同的45-型子圖

4 334-型極大平面圖著色性質(zhì)

在擴4-輪運算過程中，對象子圖2-長路的內(nèi)點被劃開成為2個頂點，如圖9所示，將該內(nèi)點稱為擴點，由劃開產(chǎn)生的2個頂點稱為擴點的拷貝頂點。類似，把擴5-輪運算對象子圖的漏腰稱為擴點，擴點被劃開后產(chǎn)生的2個頂點稱為擴點的拷貝頂點。

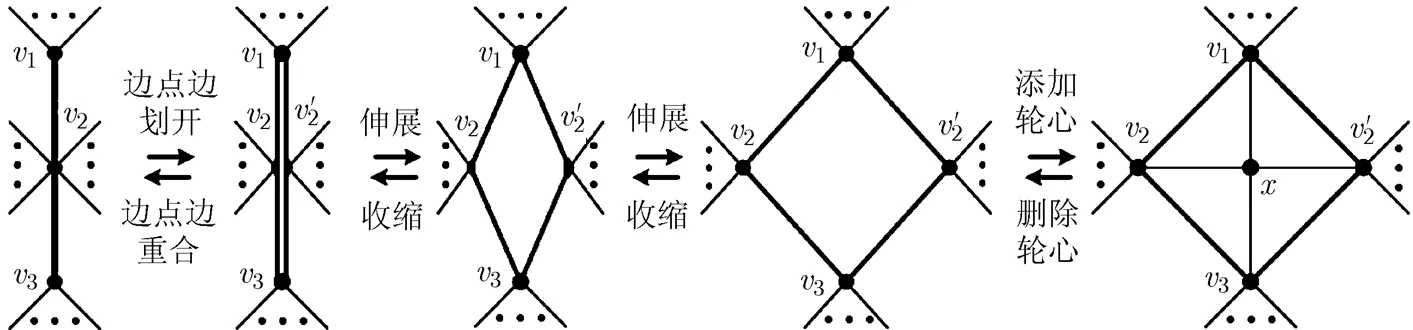
圖9 擴縮4-輪運算的示意圖

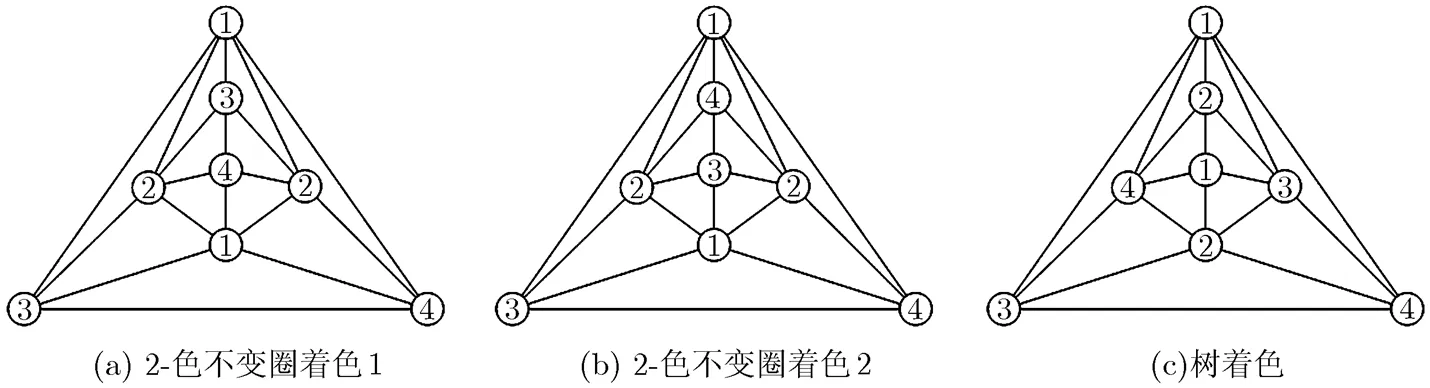
圖10 的所有著色

定理5 每個334-型極大平面圖均是樹型2-色不變?nèi)χ?/p>

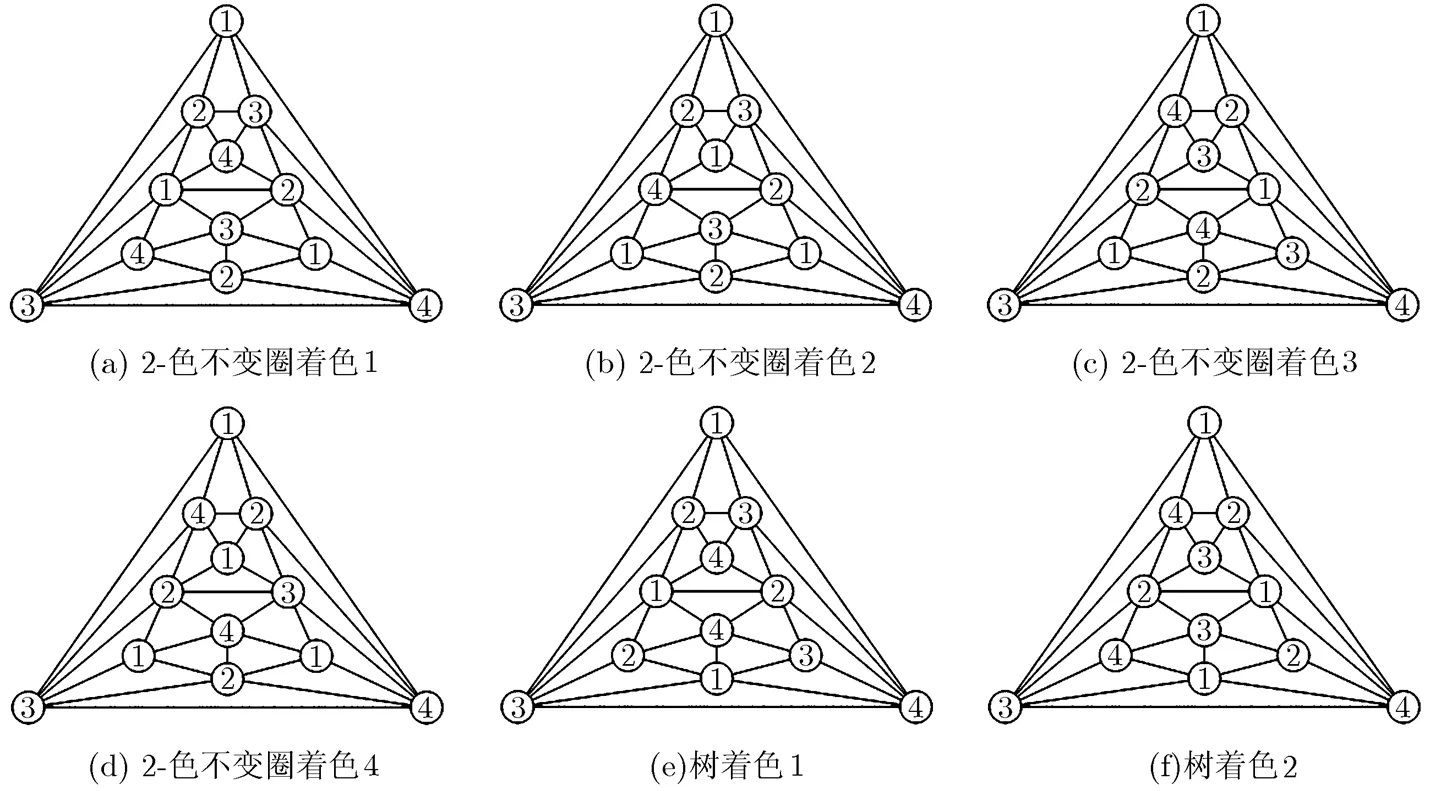
圖11 的所有著色

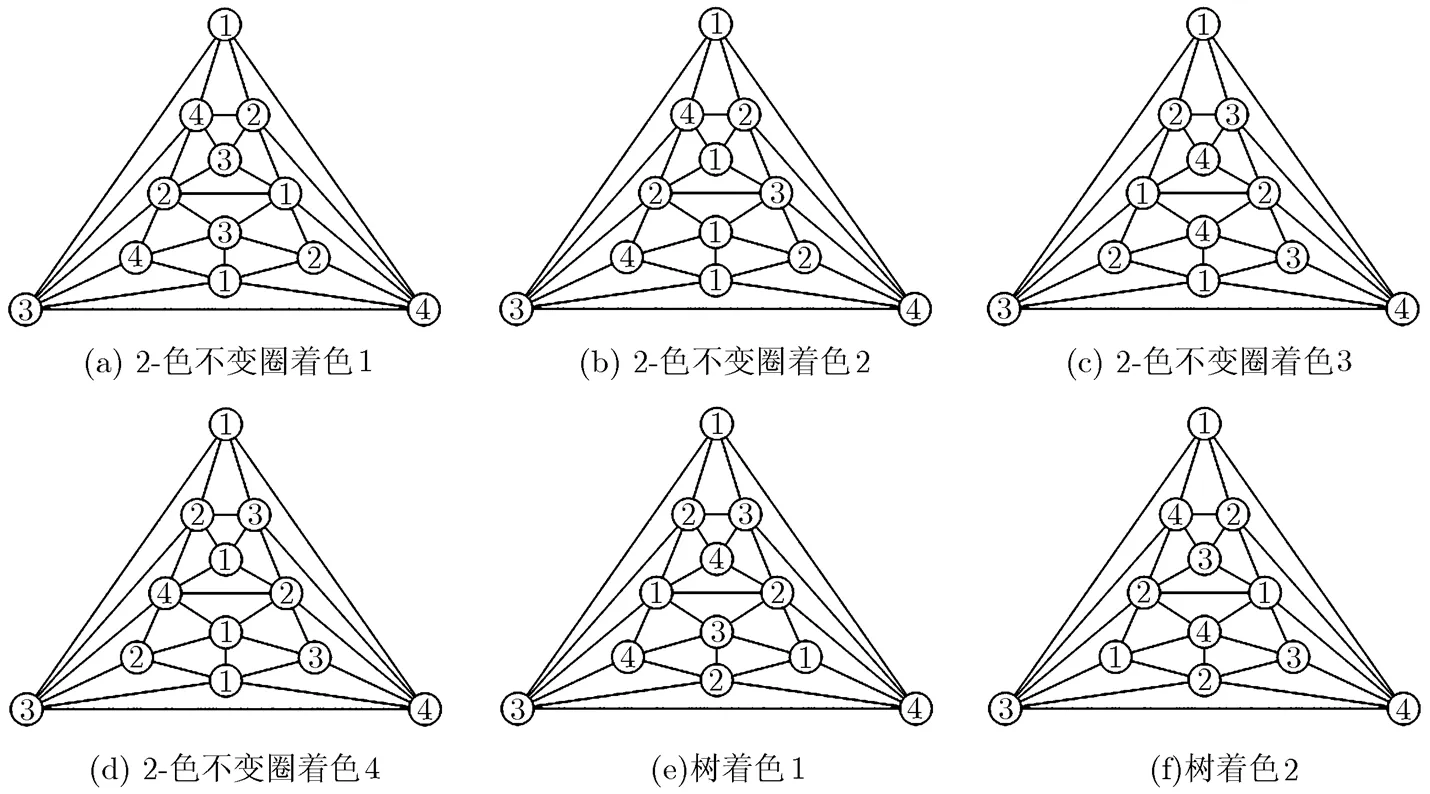
圖12 的所有著色

證畢

5 構(gòu)造純樹著色極大平面圖

利用334擴輪運算，除了構(gòu)造334-型極大平面圖，還可以構(gòu)造其它非常重要的圖類，例如，純樹著色極大平面圖。7至11階最小度的極大平面圖共有54個[14]，其中純樹著色的圖只有1個[6,7]，記作，如圖13(a)所示。共有3個45-型子圖。對其中的任意一個45-型子圖實施334擴輪運算，均得到如圖13(b)所示的13-階純樹著色極大平面圖，記為。

由定理5知，從一個最小度為4的8-階樹型2-色不變?nèi)χ珮O大平面圖出發(fā)，實施任意次數(shù)的334擴輪運算后，所得之圖均是樹型2-色不變?nèi)χ模辉儆啥ɡ?知，從一個最小度為4的9-階純樹著色極大平面圖出發(fā)，實施任意次數(shù)的334擴輪運算后，所得之圖也都是純樹著色的。基于這些結(jié)論，我們進一步提出如下猜想：

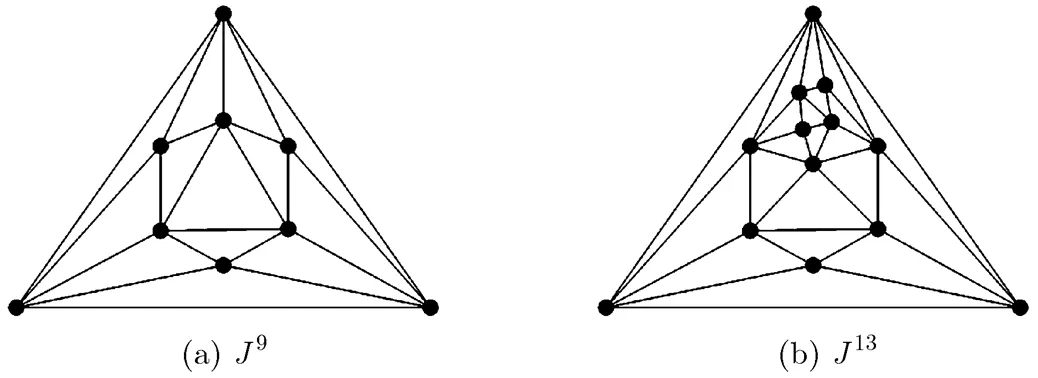
圖13 和

6 結(jié)束語

本文給出了一種稱為334擴縮運算的擴縮運算，它能夠構(gòu)造具有相同著色類型的4-色極大平面圖。在后續(xù)工作中，我們將對文中給出的猜想予以論證，并進一步研究不同著色類型圖所具有的特殊性質(zhì)。

[1] MOHAR B. Kempe Equivalence of Colorings[M]. Graph Theory in Paris. Birkh?user Basel, 2006: 287-297. doi: 10.1007/978-3-7643-7400-6_22.

[2] VERGNAS M L and MEYNIEL H. Kempe classes and the Hadwiger conjecture[J]., 1981, 31(1): 95-104. doi: 10.1016/S0095-8956(81) 80014-7.

[3] FEGHALI C, JOHNSON M, and PAULUSMA D. Kempe equivalence of colourings of cubic graphs[J]., 2015, 49: 243-249. doi: 10.1016/ j.endm.2015.06.034.

[4] MCDONALD J, MOHAR B, and SCHEIDE D. Kempe equivalence of edge-colorings in subcubic and subquartic graphs[J]., 2012, 70(2): 226-239. doi: 10.1002/jgt.20613.

[5] BELCASTRO S M and HAAS R. Counting edge-Kempe- equivalence classes for 3-edge-colored cubic graphs[J]., 2014, 325(13): 77-84. doi: 10.1016/ j.disc.2014.02.014.

[6] 許進. 極大平面圖的結(jié)構(gòu)與著色理論(3): 純樹著色與唯一4-色極大平面圖猜想[J]. 電子與信息學(xué)報, 2016, 38(6): 1328-1353. doi: 10.11999/JEIT160409.

XU J. Theory on structure and coloring of maximal planar graphs(3): Purely tree-colorable and uniquely 4-colorable maximal planar graph conjectures[J].&, 2016, 38(6): 1328-1353. doi: 10.11999/JEIT160409.

[7] XU J, LI Z P, and ZHU E Q. On purely tree-colorable planar graphs[J]., 2016, 116(8): 532-536. doi: 10.1016/j.ipl.2016.03.011.

[8] GREENWELL D and KRONK H V. Uniquely line-colorable graphs[J]., 1973, 16(4): 525-529. doi: 10.4153/CMB-1973-086-2.

[9] THOMASON A G. Hamiltonian cycles and uniquely edge colourable graphs[J]., 1978, 3: 259-268. doi:10.1016/S0167-5060(08)70511-9.

[10] FIORINI S and WILSON R J. Edge colouring of graphs[J]., 1977, 23(1): 237-239.

[11] FISK S. Geometric coloring theory[J]., 1977, 24(3): 298-340. doi: 10.1016/0001-8708 (77)90061-5.

[12] TOMMY R J and BJARNE T. Graph Coloring Problems[M].New York: USA, John Wiley & Sons, Inc., 1994: 1-295.

XU J. Theory on structure and coloring of maximal planar graphs (4):-operations and Kempe equivalent classes[J].&, 2016, 38(7): 1557-1585. doi: 10.11999/JEIT160483.

[14] 許進. 極大平面圖的結(jié)構(gòu)與著色理論(2): 多米諾構(gòu)形與擴縮運算[J]. 電子與信息學(xué)報, 2016, 38(6): 1271-1327. doi: 10.11999/JEIT160224.

XU J. Theory on structure and coloring of maximal planar graphs(2): Domino configurations and extending-contracting operations[J].&, 2016, 38(6): 1271-1327. doi: 10.11999/JEIT 160224.

[15] BONDY J A and MURTY U S R. Graph Theory[M]. New York: USA, Springer, 2008: 8-200.

劉小青： 女，1986年生，博士生，研究方向為圖論與組合優(yōu)化.

許 進： 男，1959年生，教授，研究方向為圖論與組合優(yōu)化、生物計算機、社交網(wǎng)絡(luò)與信息安全等.

Special Type of Domino Extending-contracting Operations

LIU Xiaoqing XU Jin

(,,100871,);(,,100871,)

In this paper, a new domino extending-contracting operation, called 334 extending-contracting operation, is put forward, on the basis of which, it is proposed to construct a particular kind of graphs, i.e., 334-type maximal planar graphs, and proved that all those graphs are tree-type and 2-chromatic cycle-unchanged colored and every 334-type maximal planar graphs of orderhas exactly2-chromatic cycled-unchanged colorings andtree-colorings. Additionally, it is proved that an infinite family of purely tree-colored graphs can be generated by implementing a series of 334 extending-wheel operations, and conjectured that if a maximal planar graphis purely tree-colored (purely cycle-colored or impure-colored), then the graph obtained by implementing one 334 extending-wheel (contracting-wheel) operation onis still purely tree-colored (purely cycle-colored or impure-colored).

Semi-funnels; Tree-type and 2-chromatic cycle-unchanged colored; Purely tree-colored; 334 extending- wheel operations

O157.5

A

1009-5896(2017)01-0221-10

10.11999/JEIT160886

2016-08-29；改回日期：2016-12-06；

2016-12-14

許進 jxu@pku.edu.cn

國家973計劃項目(2013CB329600)，國家自然科學(xué)基金(61372191, 61472012, 61472433, 61572046, 61502012, 61572492, 61572153, 61402437)

The National 973 Program of China (2013CB329600), The National Natural Science Foundation of China (61372191, 61472012, 61472433, 61572046, 61502012, 61572492, 61572153, 61402437)