以問題為核心上好初中幾何復(fù)習(xí)課

劉長良

以問題為核心上好初中幾何復(fù)習(xí)課

劉長良

問題是思維的核心，精心設(shè)計(jì)一個好的問題，運(yùn)用恰當(dāng)?shù)姆椒ǎ芤I(lǐng)學(xué)生輕松愉快地串連相關(guān)知識點(diǎn)、串聯(lián)形異質(zhì)同的問題，解決復(fù)雜的相關(guān)問題和生活中的實(shí)際問題，如復(fù)習(xí)“圓的有關(guān)性質(zhì)”時，可以運(yùn)用如下方法。

一、尋求多解，串聯(lián)知識方法

例題：如圖已知：△ABC是⊙O的內(nèi)接三角形，AD是高，AE是⊙O的直徑，求證AB·AC＝AD·AE

解法一：連結(jié)BE，∵AE是⊙O的直徑，∴∠ABE＝∠ADC＝90°，又∵∠E＝∠C，∴△ABE∽△ADC，∴，∴AB·AC＝AD·AE

反思解題過程回顧所用知識點(diǎn)和解題技巧：圓周角定理及其推論、圓心角定理、垂徑定理、相似三角形判定及性質(zhì)；添加輔助線技巧；作弦心距、構(gòu)成直徑所對的圓心角是常用輔助線作法。

二、探究變式，串聯(lián)形異質(zhì)同問題

根據(jù)問題特征，變化圖形，串聯(lián)形異質(zhì)同問題。通過問題變式和解答，不但能使學(xué)生迅速解答難度較大的問題，而且能有效培養(yǎng)學(xué)生探究發(fā)現(xiàn)問題的能力，激發(fā)學(xué)生興趣。針對以上問題作下列變式：

變式一：如圖2已知：△ABC是⊙O的內(nèi)接三角形，AD是高，BE是⊙O的直徑，

求證：AB·AC＝AD·BE

變式二：如圖3已知：△ABC是⊙O的內(nèi)接三角形，以A為圓心作⊙A，使⊙A與BC邊相切于點(diǎn)D，⊙A的半徑為r，作⊙O的直徑AE，

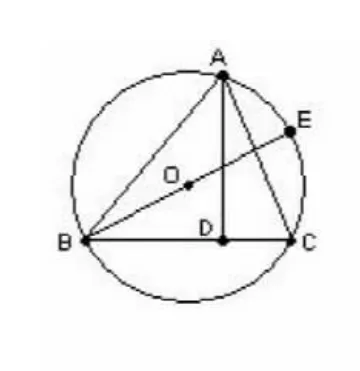
圖2

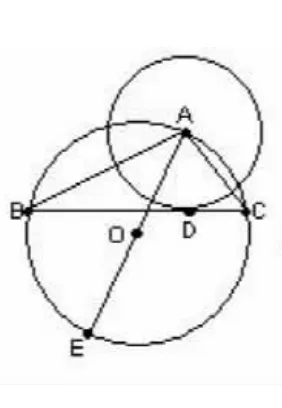
圖3

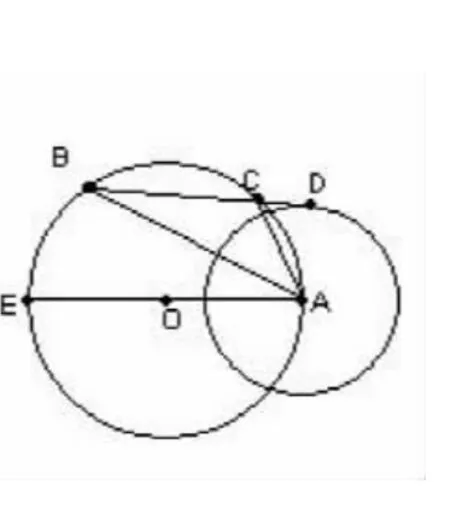
圖4

求證：AB·AC＝AE·r。

變式三：如圖4已知：△ABC是⊙O的內(nèi)接三角形，以A為圓心作⊙A，使⊙A與BC邊的延長線相切于點(diǎn)D，⊙A的半徑為r，作⊙O的直徑AE，

求證：AB·AC＝AE·r。

三、運(yùn)用結(jié)論，迅速解決復(fù)雜問題

1.解決函數(shù)最值問題

如圖5、已知：△ABC是⊙O的內(nèi)接三角形，AD是高，AB+AC＝12，AD＝3，設(shè)⊙O的半徑為y，AB的長為x。

（1）求y與x的函數(shù)關(guān)系式；

（2）當(dāng)x取何值時，⊙O的面積最大，并求⊙O的最大面積。

2.設(shè)計(jì)圓半徑的測量方案

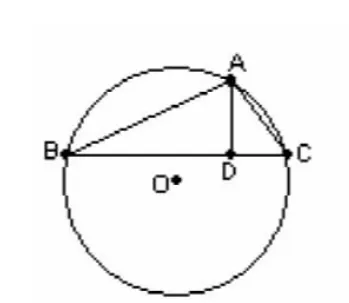
圖5

圖6

圖6 所示的是一個殘缺的機(jī)器輪子，現(xiàn)在手中只有標(biāo)有刻度的尺子，請你設(shè)計(jì)測量機(jī)器輪子半徑的方案，并求出輪子的半徑。

上數(shù)學(xué)復(fù)習(xí)課時，設(shè)計(jì)一個好的數(shù)學(xué)問題，讓學(xué)生盡可能多的尋求多種解法，針對問題廣泛聯(lián)想，探究變式，注重結(jié)論在相關(guān)問題中的應(yīng)用，能調(diào)動學(xué)生的學(xué)習(xí)積極性，大大提高復(fù)習(xí)效率，有效培養(yǎng)學(xué)生的創(chuàng)造性思維能力。

（作者單位：山東蒙陰縣孟良崮中學(xué)）