基于優化設計的門式卸車機結構可靠性分析

李永華,梁校嘉,周 峰,陳秉智(.大連交通大學 交通運輸工程學院,遼寧 大連 608; .大連交通大學 機械工程學院,遼寧 大連 608)

基于優化設計的門式卸車機結構可靠性分析

李永華1,梁校嘉1,周 峰2,陳秉智1
(1.大連交通大學 交通運輸工程學院,遼寧 大連 116028; 2.大連交通大學 機械工程學院,遼寧 大連 116028)

將優化設計與可靠性理論相結合進行門式卸車機的結構可靠性分析.利用ANSYS Workbench進行參數化實體建模,采用中心復合設計擬合響應面并進行參數靈敏度分析,在此基礎上分別使用Screening，MOGA及NLPQL 3種算法對參數尺寸進行優化和對比分析,得到最佳設計方案,在保證滿足強度要求的條件下,減小卸車機體積.再根據優化分析的結果,以最大等效應力不超過材料許用應力為可靠性評定指標,使用六西格瑪分析技術比較模型優化前后的結構可靠性,優化后的結構可靠性有所提高.在分析結構輕量化問題的同時考慮了其安全可靠性要求,為卸車機的制造與優化改進提供了理論指導.

門式卸車機; 參數化; 優化設計; 結構可靠性

門式卸車機作為卸車機的一種重要結構形式被廣泛應用于現代工業生產,是承擔運料卸料任務的重要卸車設備[1].通常采用經驗設計法確定結構配置方案,增大了安全系數,使得設計結果具有較大的盲目性,在實際生產中可能出現加強裕度過大、浪費材料的現象[2-3].由于其結構復雜,在制造過程中產生的誤差所導致的尺寸不確定性對其結構可靠性也會造成一定影響[4].因此,節約材料,降低制造成本，同時保證其結構安全可靠是卸車機設計過程中亟待解決的問題.

一些學者對大型裝卸設備,尤其是起重機行業的輕量化設計及可靠性分析方面進行了較多的研究.焦洪宇等[5]基于變密度法,在橋式起重機箱型主梁腹板處劃分若干子域,通過周期性拓撲優化數學模型,得到輕量化的主梁最優拓撲形式.劉全興等[6]從設計計算方法、結構、材料、工藝等方面對起重機輕量化設計研究進行了論述和評論.楊瑞鋼等[7]依據時變可靠性理論,研究橋式起重機金屬結構抗力時變模型與載荷時變模型,通過計算不同金屬結構抗力衰減系數下的結構可靠度,發現隨著抗力衰減系數的增加,橋式起重機金屬結構可靠度逐漸降低.李金平等[8]通過擬合響應面,結合一次二階矩法,計算起重機臂架中壓彎桿件穩定性為失效模式的可靠度.目前對卸車機設備進行上述相關方面的研究很少見到,有必要對其深入研究.

本文通過Finite Element Modeler(FEM)模塊對有限元劃分后的網格進行幾何重塑,快速轉化為可參數化實體,設定主梁與端梁的截面尺寸作為輸入參數,在保證結構強度的前提下,以體積最小為目標,進行結構優化.然后使用六西格瑪模塊(Six Sigma Analysis,SSA)對優化前后的結構進行可靠性評估.該過程避免了使用三維繪圖軟件對卸車機進行參數化建模,提高了設計效率,并考慮到優化后的結構的可靠性是否滿足要求,給出一個較合理的設計方案.

1 門式卸車機有限元分析

1.1門式卸車機參數化模型建立

本文采用的門式卸車機模型主要由心盤、主梁、端梁及支腿組成,如圖1所示.

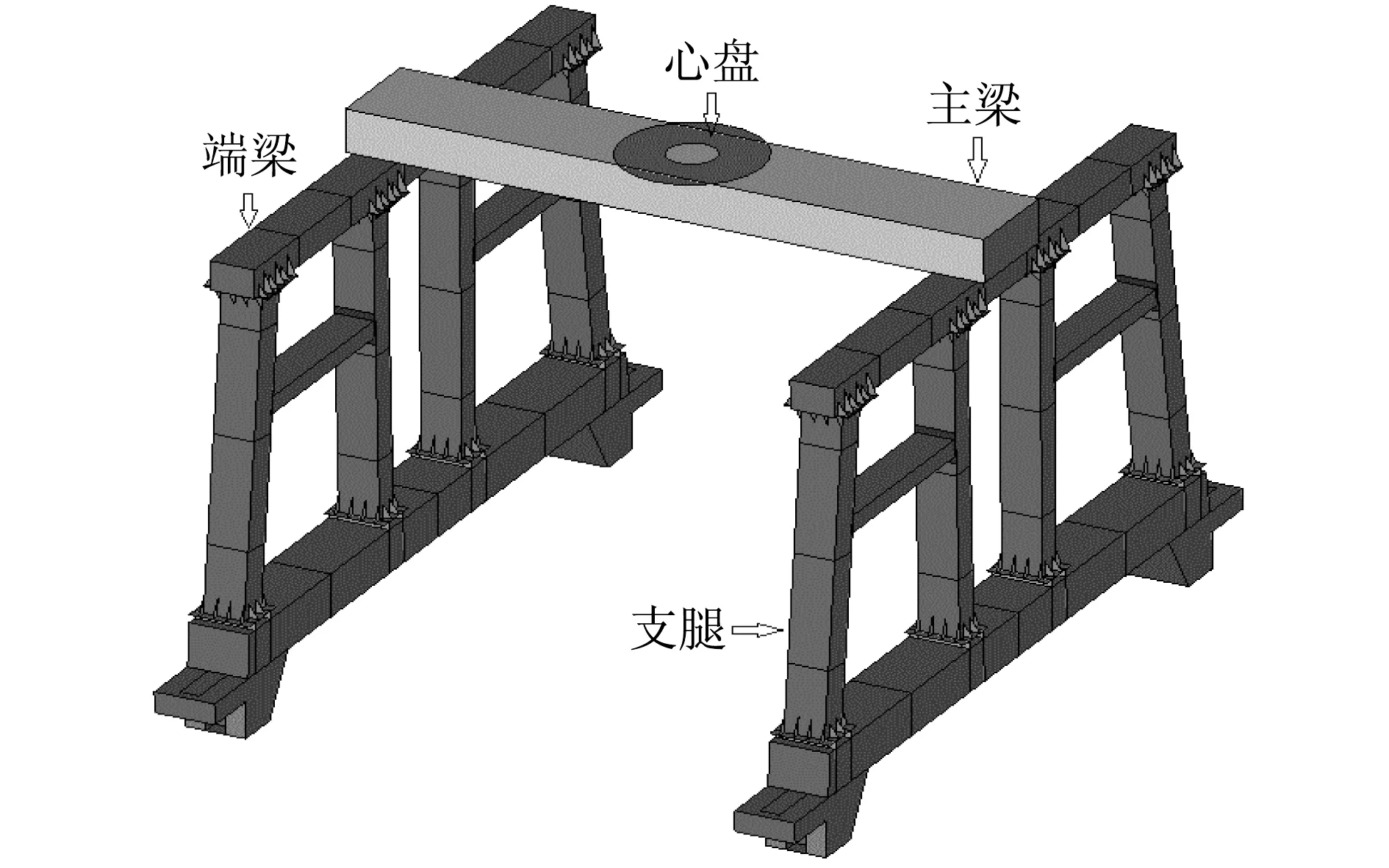
圖1 門式卸車機模型Fig.1 Model of gantry unloader

該模型采用Shell63單元劃分,將cdb文件導入Workbench中的FEM模塊生成幾何模型,為之后的模型參數化提供幾何基礎,并在Static Structural模塊中進行參數化設計及相關力學分析計算,建立對應關系,當參數變化時,對應的數據也會發生相應變化[9].這里選取模型的心盤厚度XinPan、主梁上蓋板厚度SGB、主梁左腹板厚度ZFB、左端梁板厚度b2、右端梁板厚度b1、主梁右腹板厚度YFB及主梁下蓋板厚度XGB 7個參量作為輸入變量.

該卸車機模型材料選用WEL590號鋼,其材料屬性主要參數如表1所示.

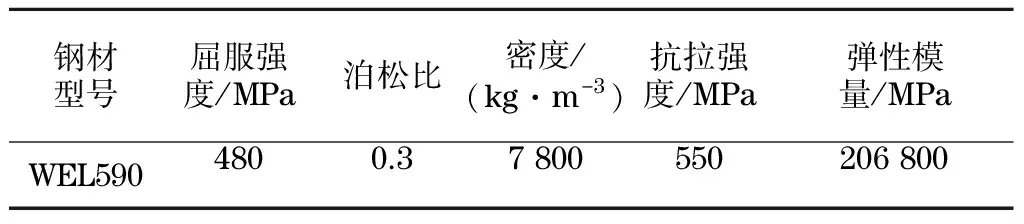
表1 WEL590號鋼材料屬性Tab.1 Material properties of WEL590 steel

1.2載荷施加及約束

將重新生成的參數化模型導入Static Structural模塊,施加邊界條件.在危險工況下,對梁中部心盤施加向下的集中力FZ=-29 300 N和繞軸線的轉矩MX=-7.5e+007 N·mm,行走機構4個支腿輪處斷面施加固定約束,如圖2所示.

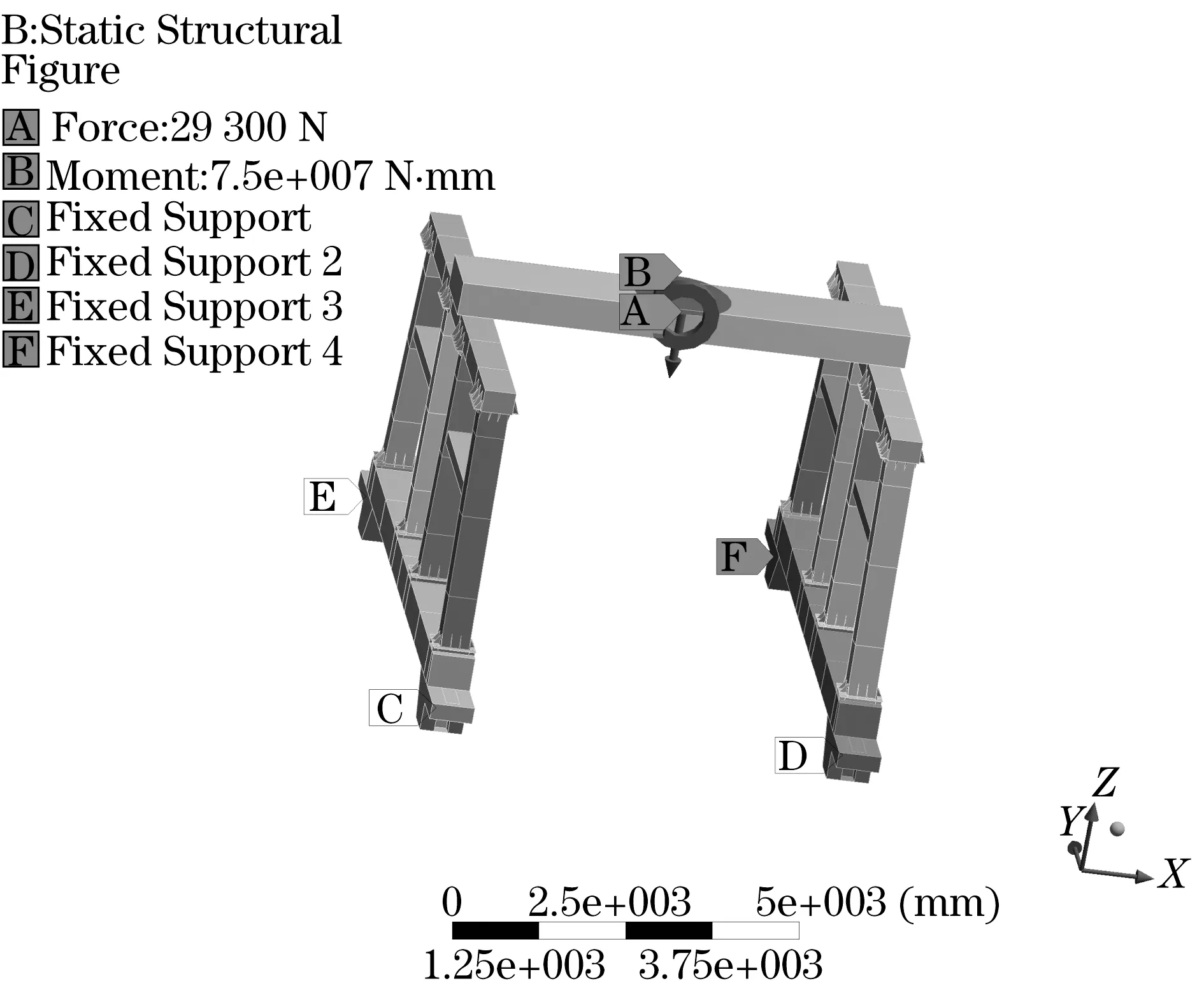
圖2 施加力與約束Fig.2 Applied loads and constraints

從圖3可以看出,最大等效應力為315.05 MPa,受力部位在心盤處.這里選擇最大等效應力Smax和模型體積Volume作為輸出變量.

對于σs/σb=480/550=0.87>0.7的鋼材,其基本許用應力[σ]按下式計算[10]:

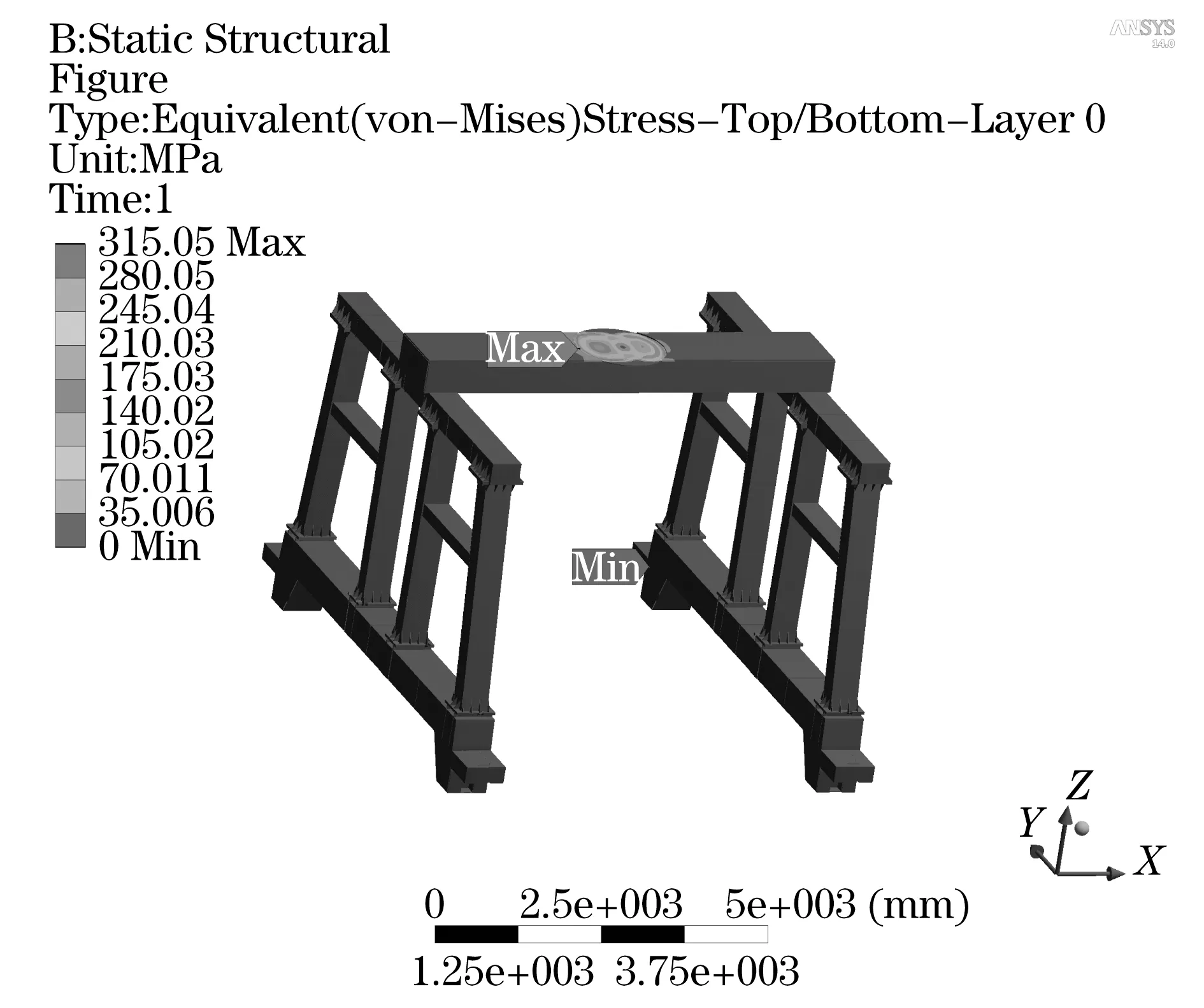
圖3 卸車機受力分布圖Fig.3 Equivalent stress nephogram of unloader

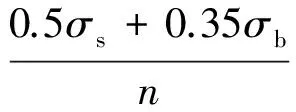
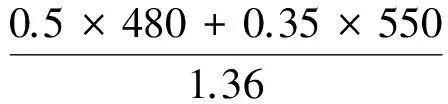
式中:n取1.36.

由于Smax<[σ],其結構滿足強度要求且具有一定的冗余量,可以對結構進行輕量化設計.

2 響應面擬合及靈敏度分析

運用Design Exploration優化模塊,以試驗設計為基礎擬合響應面,能夠真實地反映設計變量與響應之間的關系[11].首先定義各輸入變量的取值范圍,通過計算參數的響應值,得到各參數的靈敏度,從而確定變量對優化目標的影響程度.

表2為7個變量的取值范圍,根據實際生產設計要求確定.因靈敏度分析的需要,定義各輸入變量為連續型變量.

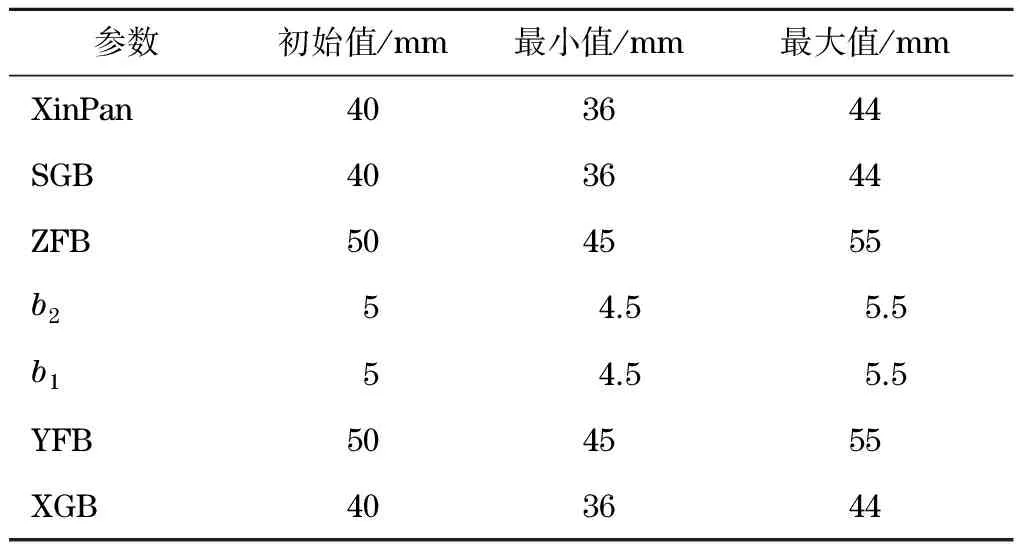
表2 輸入參數設置Tab.2 Input parameter settings

采用中心復合設計(Central Composite Design,CCD)擬合響應面,利用試驗數據擬合多項式方程,用方差分析評估擬合效果[12].進行79次試驗設計,計算結束后,通過各輸入點及響應值擬合響應面,優化設計即根據優化準則從擬合出的響應面上尋找最優區域[2].圖4和圖5分別是最大等效應力Smax和模型體積Volume的響應面.

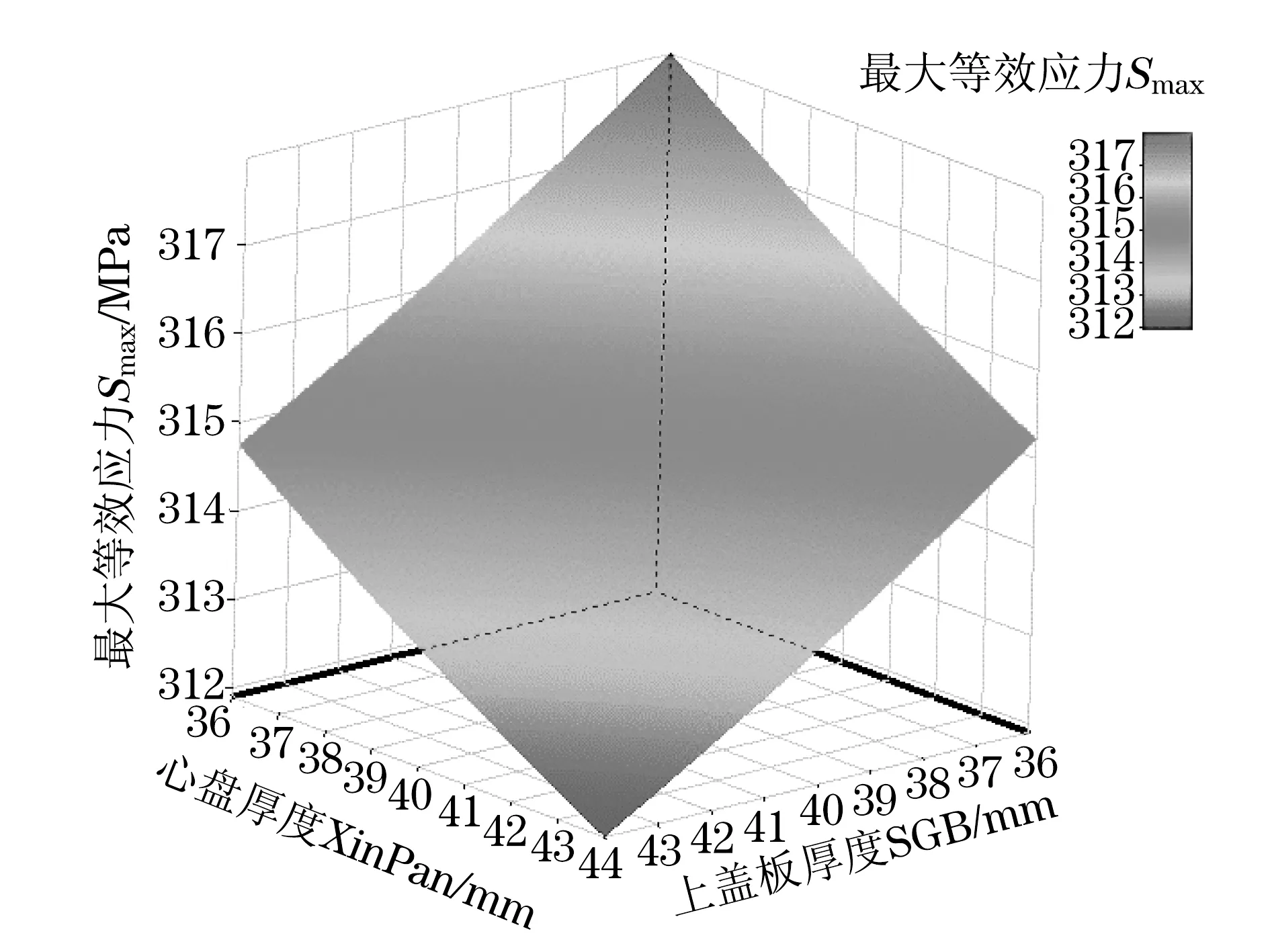
圖4 最大等效應力響應面Fig.4 Response surface of maximum equivalent stress

圖5 模型體積響應面Fig.5 Response surface of model volume

由圖4可知,隨主梁心盤XinPan和主梁上蓋板厚度SGB的增大,卸車機最大等效應力呈減小趨勢.由圖5可知,隨主梁下蓋板厚度XGB和左腹板板厚ZFB的增大,卸車機體積呈增大趨勢.兩個響應面幾乎是平面,輸入變量對響應的影響是線性的,因此其擬合精度也較高.

此外,根據計算輸出的結果,可給出各個輸入參數的靈敏度,使其在一張圖中顯示出來,能夠更加直觀地表現出參數對響應的影響,如圖6所示.

在圖6中,各輸入變量與最大等效應力呈反比關系,與卸車機體積呈正比關系.靈敏度分析圖顯示的趨勢與之前響應面的分析結果相吻合,其中左端梁板厚度b2對最大等效應力影響最大,為保障結構強度,可適當增加其厚度,減小其余參量厚度,為之后的優化提供一個可行設計思路.

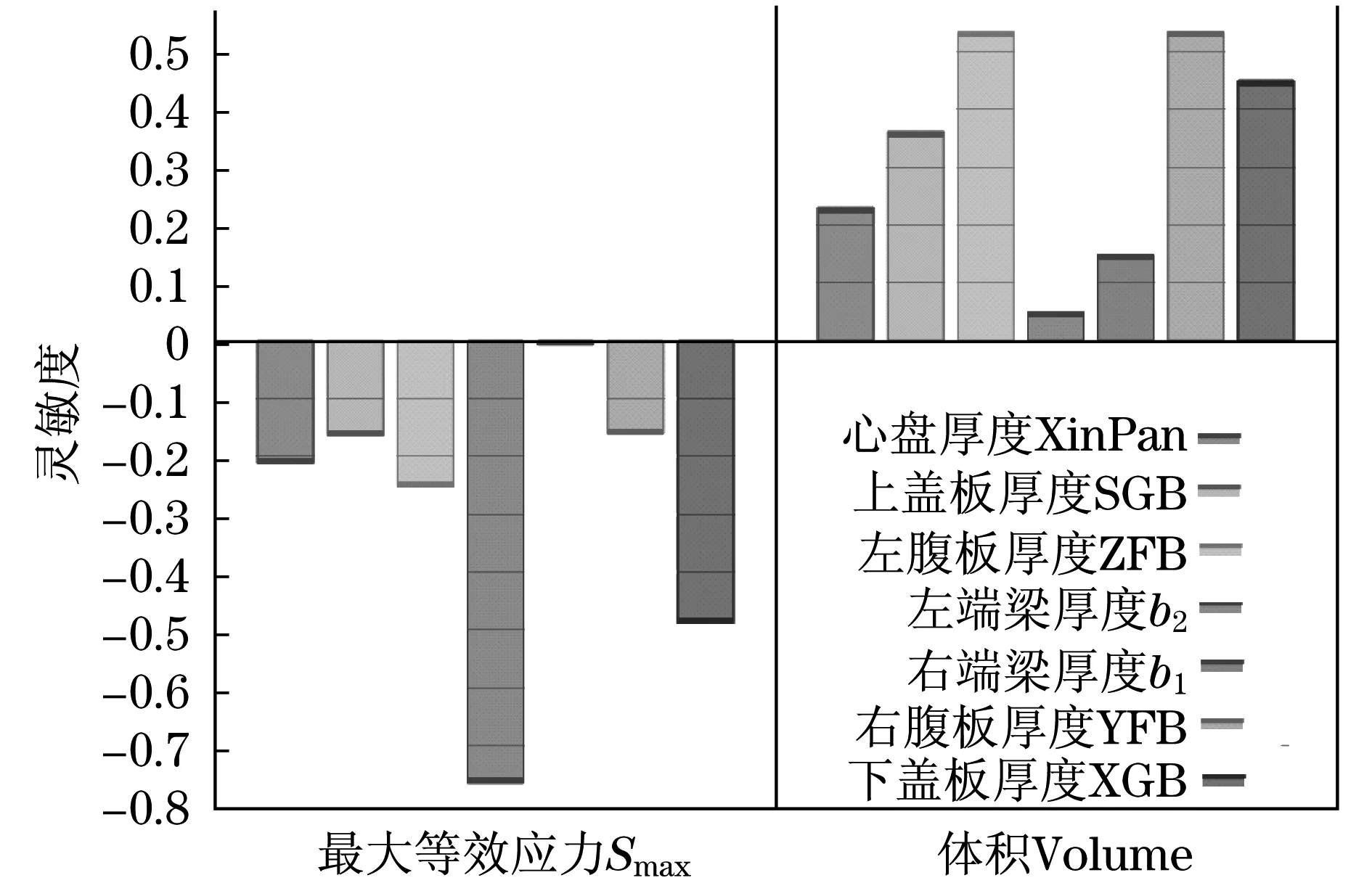
圖6 靈敏度分析Fig.6 Sensitivity analysis

3 結構優化方案設計

擬合出響應面之后,使用目標驅動優化模塊進行結構優化.進行優化前,設置各輸入變量的取值范圍(見表2),重要程度為默認值,優化目標是:在保證卸車機最大等效應力不大于318 MPa的前提下,使體積達到最小為目標.在Workbench目標驅動優化模塊中,有3種優化算法,分別是Screening(篩選)、MOGA(多目標遺傳算法)及NLPQL(二次拉格朗日非線性規劃)算法.本文利用這3種算法優化卸車機模型,以得到期望的目標值.以下是這3種方法簡介及啟用算法的相關設置.

Screening優化方法是基于采樣和排序的簡單方法,它支持多種目標和約束以及所有類型的輸入參數.因準確度與采樣數有關,設置采樣集大小為1 000.

MOGA是基于NSGA-Ⅱ(非支配排序遺傳算法Ⅱ)的一個變種.它支持多種目標和約束,在較大的設計變量空間內迅速尋優,非常適合用于計算全局最大值/最小值[13],同時可以規避局部最優的陷阱,通過快速排序找到非支配解，保留精英群體和維持種群的多樣性[14].雖然本文中的優化目標只有一個,即模型體積,但仍可以啟用MOGA算法進行優化.相關設置如下:最大迭代次數20次,初始樣本點1 000個.

NLPQL是一種基于梯度的算法,提供一個精致的優化結果.該算法的基礎是擬牛頓法,支持單目標,多約束并要求輸入輸出參數保持連續,將目標函數展開成二階Taylor級數形式,線性化約束條件,使非線性問題轉化為二次規劃問題,對二次規劃進行求解,得到所需設計點[15].迭代次數設置為20次,收斂條件設為1E-06,初始樣本點1 000個.

從Screening和MOGA方案各產生的3組候選點中選擇2組較優設計點與NLPQL方案產生的單組候選點進行對比,結果如表3所示.

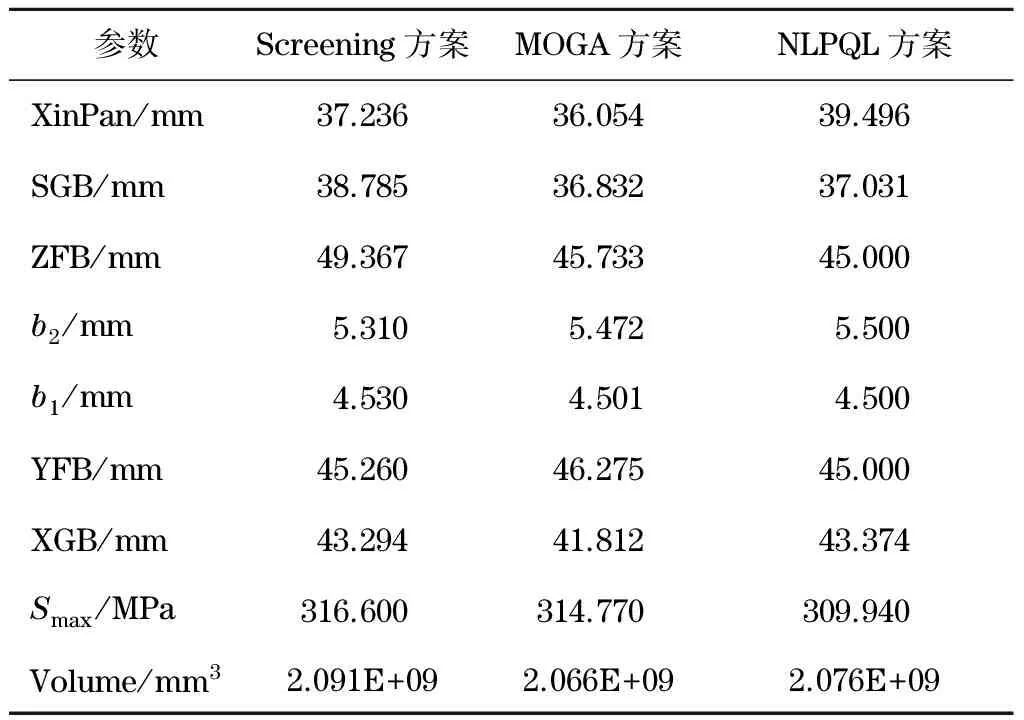
表3 設計方案Tab.3 Design schemes

對比表3列出的3種優化設計結果,得到MOGA算法使卸車機體積達到最小.將該設計方案作為當前設計重新生成幾何模型,并對新生成的模型再次進行有限元強度校核.

如圖7所示,卸車機模型重新生成后,其最大受力位置由之前的心盤部位變為主梁與左端梁的交界部位,最大等效應力為314.79 MPa,小于材料的許用應力,滿足強度要求.卸車機結構優化前后的各參數對比結果如表4所示.

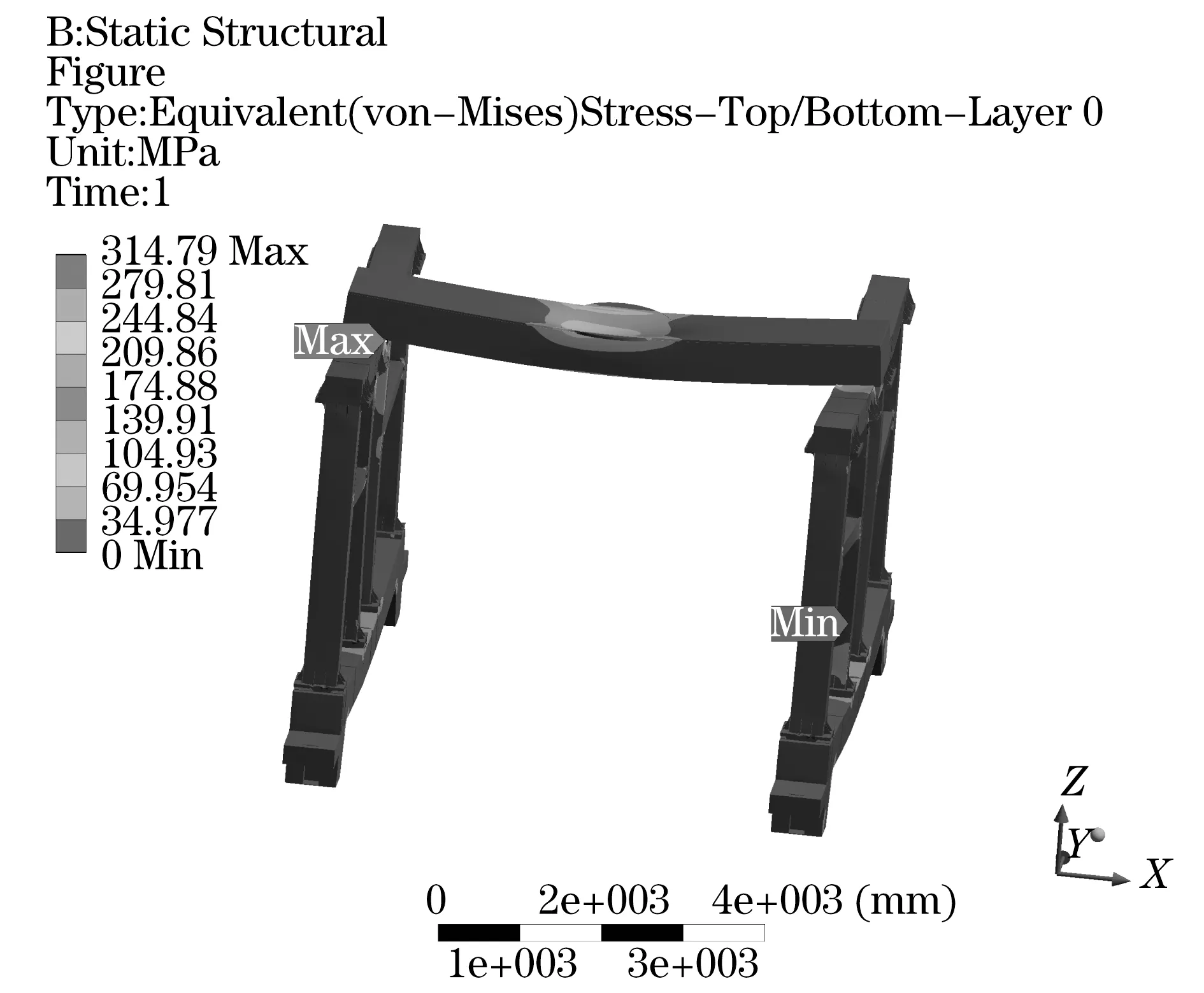
圖7 卸車機受力分布圖Fig.7 Equivalent stress nephogram of unloader

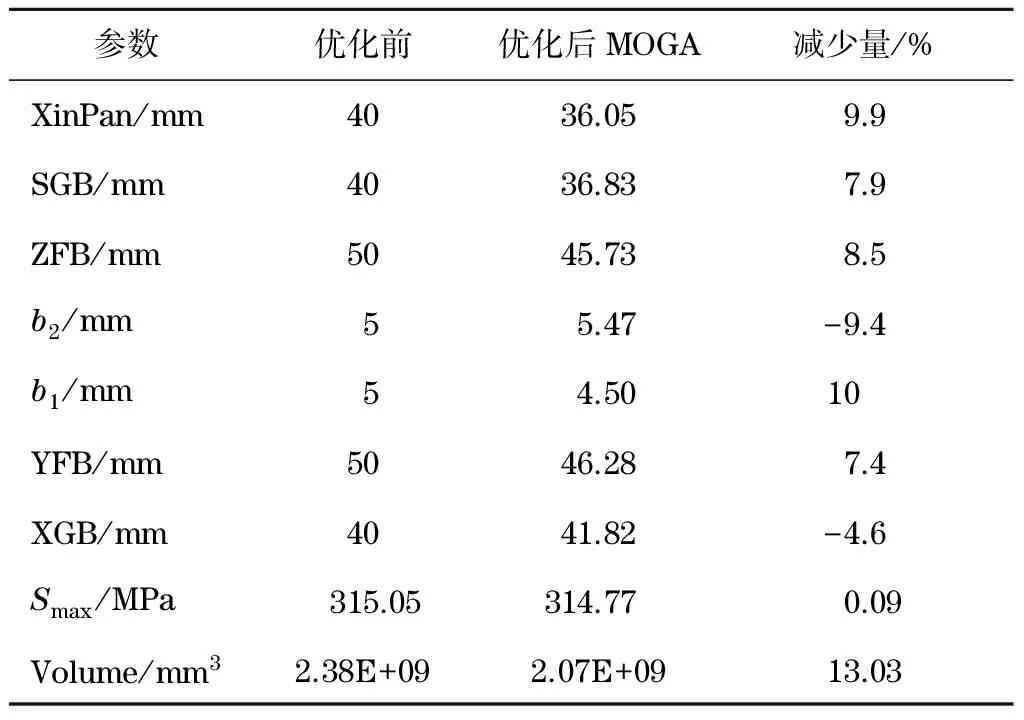
表4 優化前后參數對比Tab.4 Comparison of parameters before andafter optimization

根據表4可以得出,經過優化處理后,輸入變量中除了左端梁板厚度b2和下蓋板厚度XGB外,其余各輸入變量均有所減小,卸車機體積較優化前減小了13.03%,達到節約成本的目的.值得注意的是,雖然各參量的厚度大多減少,但最大等效應力并沒有增大,反而減小了0.09%,這是因為對其影響最大的參量左端梁板厚度b2增大了9.4%,使得在保證強度的同時,充分減小其他參量厚度值,進而減小了模型體積,也印證了對靈敏度結果的分析.

4 卸車機結構可靠性分析

首先將對結構可靠性具有影響的隨機變量設為x1,x2,…,xn,該結構功能函數為Z=g(x1,x2,…,xn).假定R為結構強度隨機變量,S為結構承受的外部應力,則結構功能函數Z可簡化為強度隨機變量R與外部應力S的差值,表達式為:Z=R-S.應力-強度干涉模型認為,當R>S時就不會發生失效,因此Z=g(x1,x2,…,xn)>0可作為可靠性評判的標準.

六西格瑪分析技術是基于6個標準誤差理論來評估產品的可靠性是否滿足六西格瑪標準.假設材料屬性、設計尺寸、邊界條件等隨機輸入變量的分布規律,分析輸入變量不確定性對產品性能的影響,評估產品性能是否達到六西格碼質量要求.本文采用ANSYS Workbench中的SSA模塊,結合響應面與拉丁超立方抽樣技術,根據結構可靠性標準:最大等效應力Smax不大于318 MPa,比較優化前和MOGA算法優化后結構的可靠性結果,設計流程如圖8所示.

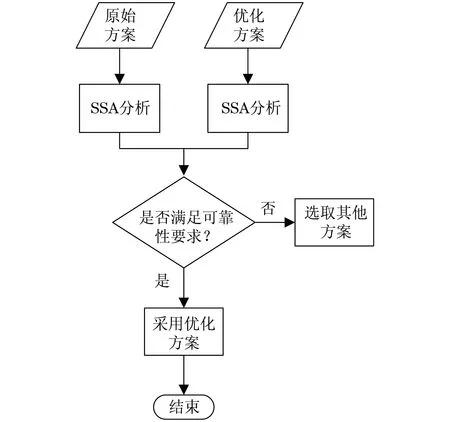
圖8 可靠性分析設計流程Fig.8 Flowchart of the reliability analysis

在制造過程中存在許多不可控因素,每個零件的尺寸會在一定范圍內波動,所以,應將尺寸作為隨機變量來處理.依據以往的實踐經驗,通常情況下可以認為尺寸服從正態分布,故選用正態分布模擬各尺寸變量的分布規律.表5為門式卸車機優化前后各參數的分布特性.

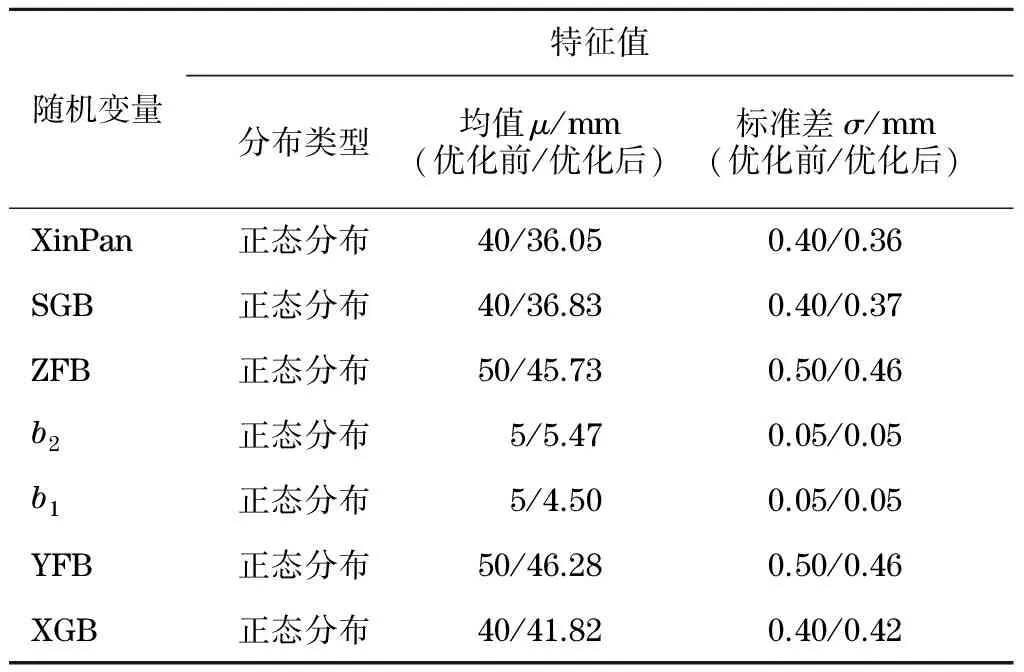
表5 各隨機變量及分布類型Tab.5 Random variables and distribution types

在SSA模塊中設置好參數后,通過中心復合設計擬合響應面,使用拉丁超立方抽樣技術抽取樣本10 000次.圖9和圖10分別是優化前和優化后的抽樣結果,這些直方圖是描述變量離散性的一種可視化方式,基本接近于正態分布曲線,分布規則且不存在較大的跳躍,說明抽樣次數足夠,滿足分析需求.

在SSA分析中,累積分布函數可以檢測零部件或產品結構是否滿足其可靠性要求,通過圖中的黑色樣本點擬合出最大等效應力的累積分布函數曲線,曲線上每一點的值表示設計變量小于該點的概率.從圖9和圖10可以看出,其許用應力318 MPa分別坐落在[60%,70%]和[70%,80%]區間范圍內,顯然,優化后的設計方案的結構可靠度有所提高.其次,利用參數概率列表可以給出更精確的可靠性數值,在參數概率列表中插入數值318,得到優化前結構可靠度為63.04%,優化后結構可靠度為76.36%.經計算,MOGA得到的最佳優化方案比原始方案的結構可靠度提高了13.32%.

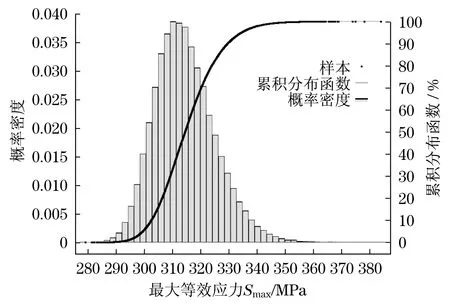
圖9 優化前最大等效應力抽樣結果Fig.9 Sampling results of maximum equivalentstress before optimization

圖10 優化后最大等效應力抽樣結果Fig.10 Sampling results of maximum equivalentstress after optimization

5 結論

(1) 在滿足結構強度的前提下,采用3種優化算法對門式卸車機進行優化,其中MOGA方案達到了最佳優化效果,使卸車機體積減小了13.03%,材料利用率得到了提高,降低生產成本,產生了一定的經濟效益.

(2) 通過六西格瑪可靠性分析知,門式卸車機經MOGA優化后比優化前的可靠性增加了13.32%,在節約成本的同時又提升了安全可靠程度,保證了該產品的質量.

(3) 將優化設計與可靠性分析技術結合應用于實際工程中,使優化后的結果更加可靠,提高了設計的合理性.

[1] 李曙光,蘇長圖,姜興軍,等.螺旋卸車機高效生產實踐[J].萊鋼科技,2009,33(1):26-28.

LI S G,SU C T,JIANG X J,et al.High-efficiency production of screw unloaders[J].Laigang Science & Technology,2009,33(1):26-28.

[2] 方鵬,李健,韋遼.基于ANSYS Workbench機床主軸有限元分析[J].裝備制造技術,2013(4):28-30.

FANG P,LI J,WEI L.Feat of machine spindle based on Ansys Workbench[J].Equipment Manufacturing Technology,2013(4):28-30.

[3] 常秋香.基于COSMOSWorks的某沖壓液壓機機身優化設計[J].熱加工工藝,2013,42(3):132-133.

CHANG Q X.Optimization design of frame of some punching hydraulic press based on COSMOSWorks[J].Hot Working Technology,2013,42(3):132-133.

[4] 張志紅,何楨,郭偉.望目特性穩健參數設計優化標準的構建[J].機械工程學報,2008,44(4):133-137. ZHANG Z H,HE Z,GUO W.Construction of optimizing standard for robust parameter design in the target being best[J].Journal of Mechanical Engineering,2008,44(4):133-137.

[5] 焦洪宇,周奇才,吳青龍,等.橋式起重機箱型主梁周期性拓撲優化設計[J].機械工程學報,2014,50(23):134-139.

JIAO H Y,ZHOU C Q,WU Q L,et al.Periodic topology optimization of the box-type girder of gridge crane[J].Journal of Mechanical Engineering,2014,50(23):134-139.

[6] 劉全興,劉蘊,殷國富.我國起重機輕量化設計研究[J].機械設計與制造工程,2016,45(5):71-73.

LIU Q X,LIU Y,YIN G F.Overview on the lightweight design of domestic cranes[J].Machine Design and Manufacturing Engineering,2016,45(5):71-73.

[7] 楊瑞剛,徐格寧,王建華,等.基于時變失效的橋式起重機結構可靠性分析[J].中國安全科學學報,2012,22(8):64-69. YANG R G,XU G N,WANG J H,et al.Analysing reliability of bridge crane steel structure based on time-varying failure theory[J].China Safety Science Journal,2012,22(8):64-69.

[8] 李金平,王建明,焦生杰,等.基于響應面法的履帶起重機桁架臂壓彎構件穩定性的可靠性分析[J].機械科學與技術,2012,31(12):1959-1962.

LI J P,WANG J M,CUI S J,et al.Reliability analysis of stability for compressive-bending member of crawler crane’s boom based on response surface method[J].Mechanical Science and Technology for Aerospace Engineering,2012,31(12):1959-1962.

[9] CAMBA J D,CONTERO M,COMPANY P.Parametric CAD modeling:an analysis of strategies for design reusability[J].Computer-Aided Design,2016,74:18-31.

[10] 國家質量監督檢驗檢疫總局.起重機設計規范:GB/T 3811—2008[S].北京:中國標準出版社,2008.

General Administration of Quality Supervision,Inspection and Quarantine of the People’s Republic of China.Design rules for cranes:GB/T 3811—2008[S].Beijing:Standards Press of China,2008.

[11] GOSWAMI S,GHOSH S,CHAKRABORTY S.Reliability analysis of structures by iterative improved response surface method[J].Structural Safety,2016,60:55-66.

[12] 劉永,李淑娟,李言,等.基于中心復合設計試驗的SiC單晶片超聲振動加工工藝參數優化[J].機械工程學報,2013,49(7):193-198.

LIU Y,LI S J,LI Y,et al.Central composite design test based process parameters optimizing for compound machining with ultrasonic vibration on SiC wafer[J].Journal of Mechanical Engineering,2013,49(7):193-198.

[13] MEZIANE-TANI I,METRIS G,LION G,et al.Optimization of small satellite constellation design for continuous mutual regional coverage with multi-objective genetic algorithm[J].International Journal of Computational Intelligence Systems,2016,9(4):627-637.

[14] 姜衡,管貽生,邱志成,等.基于響應面法的立式加工中心動靜態多目標優化[J].機械工程學報,2011,47(11):125-133.

JIANG H,GUAN Y S,QIU Z C,et al.Dynamic and static multi-objective optimization of a vertical machining center based on response surface method[J].Journal of Mechanical Engineering,2011,47(11):125-133.

[15] 肖林京,張緒帥,常龍,等.基于ANSYS和iSIGHT的磁懸浮軸承結構優化設計[J].軸承,2012(5):5-8.

XIAO L J,ZHANG X S,CHANG L,et al.Design and optimization of magnetic bearings based on ANSYS and iSIGHT[J].Bearing,2012(5):5-8.

Structuralreliabilityanalysisonportal-typeunloaderbasedonoptimizationdesign

LIYonghua1,LIANGXiaojia1,ZHOUFeng2,CHENBingzhi1
(1.School of Traffic and Transportation Engineering,Dalian Jiaotong University,Dalian 116028,Liaoning, China; 2.School of Mechanical Engineering,Dalian Jiaotong University,Dalian 116028,Liaoning, China)

The structural reliability analysis of the portal-type unloader is carried out by combining the optimization design with the reliability theory.The parametric solid model is established by ANSYS Workbench,by utilizing the central composite design to fit the response surface and parameter sensitivity analysis is performed,on the basis of this,the best design scheme is obtained by respectively using Screening,MOGA and NLPQL algorithm to optimize the parametric sizes.Under the condition that meets the requirements in strength,the volume of portal-type unloader is decreased.Then according to the results of optimization analysis,in view of the reliability evaluation criterion that the maximum equivalent stress does not exceed the allowable stress of the material,the structural reliability of the model before and after optimization is compared by using Six Sigma analysis technology and the reliability of the optimized structure is improved.In the analysis of lightweight problems of structure,while taking into account the safety and reliability requirements,a theoretical guidance is provided for the manufacturing and optimization improvement of the unloader.

portal-type unloader; parameterizing; optimization design; structural reliability

TH 24

： A

： 1672-5581(2017)03-0261-06

國家自然科學基金資助項目(11272070);遼寧省自然科學基金資助項目(2014028020);遼寧省教育廳科學研究資助項目(JDL2016001);大連市科技開發資助項目(2015A11GX026)

李永華(1971—),女,教授,博士.E-mail:yonghuali@163.com