用于冗余度機械臂避障神經網絡控制器

劉善春,李 鯉(.蘭州城市學院 培黎工程技術學院,蘭州 730070; .蘭州城市學院 培黎石油工程學院,蘭州 730070)

用于冗余度機械臂避障神經網絡控制器

劉善春1,李 鯉2
(1.蘭州城市學院 培黎工程技術學院,蘭州 730070; 2.蘭州城市學院 培黎石油工程學院,蘭州 730070)

目前,對機械臂避障控制器研究方法有多種,經分析現有的PD控制器追蹤誤差較大,效果較差.對此,提出了神經網絡控制器并對其運動過程中避障追蹤誤差進行仿真驗證.構建了機械臂轉動關節避障的動力學模型,在延伸的笛卡爾空間中定義了未知函數.使用多層感知器神經網絡逼近方法,分析了神經元自適應控制器系統的閉環穩定性,對系統的閉環穩定性進行了證明,得到了神經參數的自適應法則.結合具體實例,將機械臂避障神經網絡控制器進行仿真,結果表明,機械臂末端執行器在移動障礙物的環境下具有優良的軌跡追蹤效果.

機械臂; 神經網絡; 控制器; 避障; 自適應法則;仿真

冗余度機械臂誕生于20世紀80年代末,在90年代得到了快速發展,廣泛應用于醫療、航空、海洋等各種領域.在實際應用中,冗余度機械臂的主要優點在于它們具有靈巧性和避障能力.這主要由于它們的末端執行器的自由度數目超過了實現規定任務所需的自由度數.但是,冗余度帶來了動力學控制器合成具有復雜性.PD控制器實現比較容易,無需系統的模型,在工業應用相對廣泛,但是系統動態性相對較差.因此,高性能的機械臂控制一直是當今研究的熱點.

當前,對機械臂控制器的研究方法有多種.例如:文獻[1-3]主要研究了機械臂神經網絡控制及應用.文獻[4-6]對非完整移動機械臂考慮了一種由動力學條件耦合和輸出反饋實現的自適應運動和力控制展開研究.文獻[7-9]給出了在有不確定性和干擾存在條件下,對一個冗余驅動向移動機械手的魯棒軌跡追蹤問題.以往的研究都沒有很好地解決冗余度機械臂避障問題.對此,本文采用了神經網絡控制器對機械臂運動過程中避障進行控制.創建了冗余度機械臂避障數學模型,給出了機械臂避障的不等式.采取神經網絡逼近方法,對神經網絡控制器的穩定性進行了推導.采取3自由度機械臂避障控制器進行驗證,同時與PD控制器進行了對比.帶有神經網絡控制器的機械臂在移動障礙物的環境下追蹤誤差較小,自適應反應時間較短,效果良好.

1 機械臂避障

轉動關節自由度為n的機械臂動力模型如下:

(1)

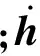
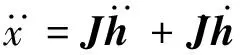
(2)

式中:J為雅可比矩陣.

如果機械臂上所有的點和一個移動障礙物間能一直保持一定間距,則機械臂在運動過程中能夠避開該障礙物[10].對障礙物,更多地采用外凸的形狀(球體、圓柱體等),特別是采用球體,因為容易計算球體和機械臂不同段之間的距離.

考慮k個障礙物被一個半徑為rj、中心分別為笛卡爾坐標xoj=(x1oj,x2oj,x3oj),j=1,2，…,k的圓柱體包圍,如圖1所示.設dj為機械臂和障礙物中心j的最小距離.為了避免機械臂和障礙物相撞,沿著軌跡分布的能足夠滿足約束條件如下:

(3)

式中:Tj為障礙物的中心與機械臂的距離平方與障礙物半徑平方之差.

2 神經網絡逼近法

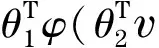
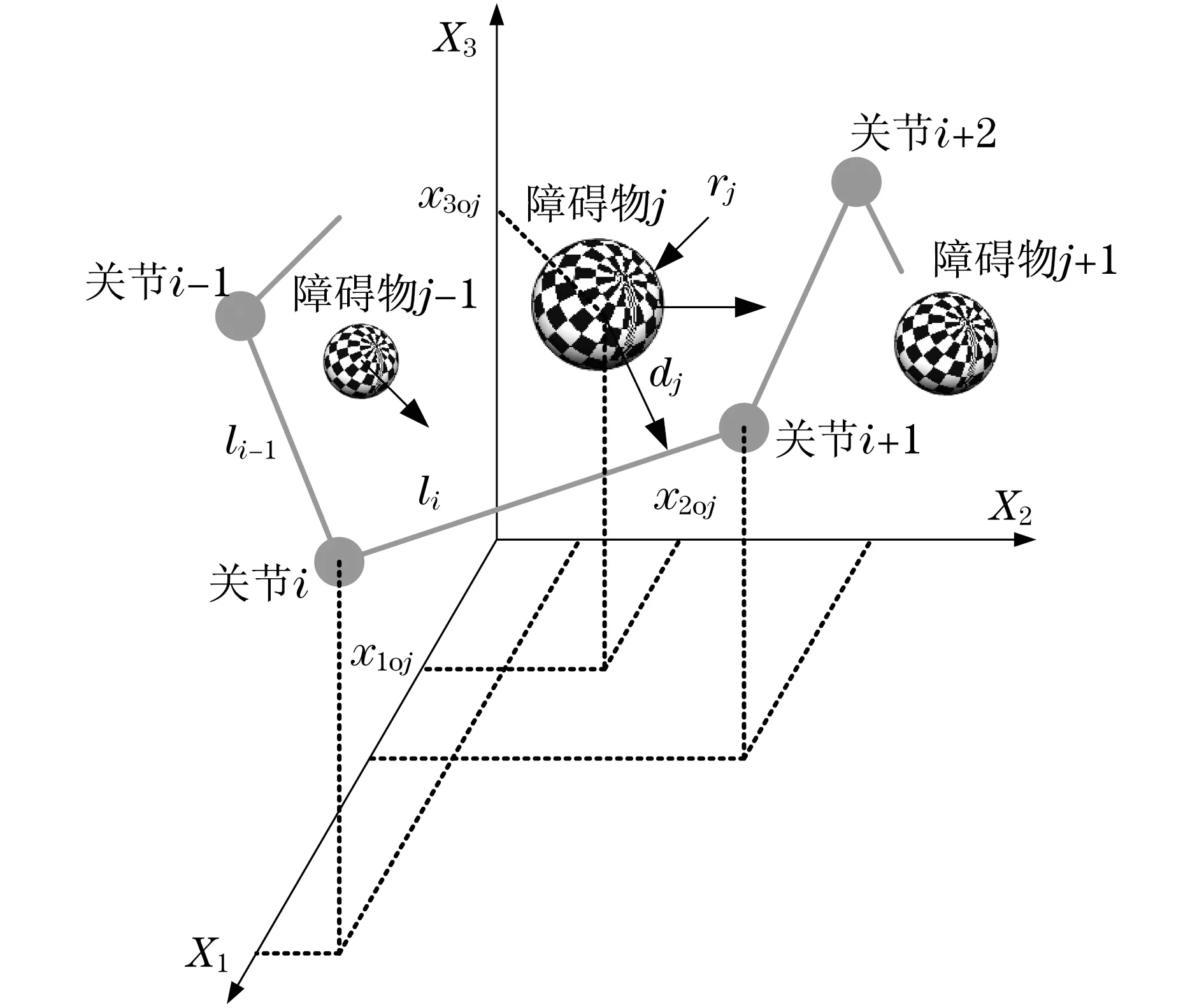
圖1 有障礙物的冗余機械臂Fig.1 A redundant manipulator with obstacles

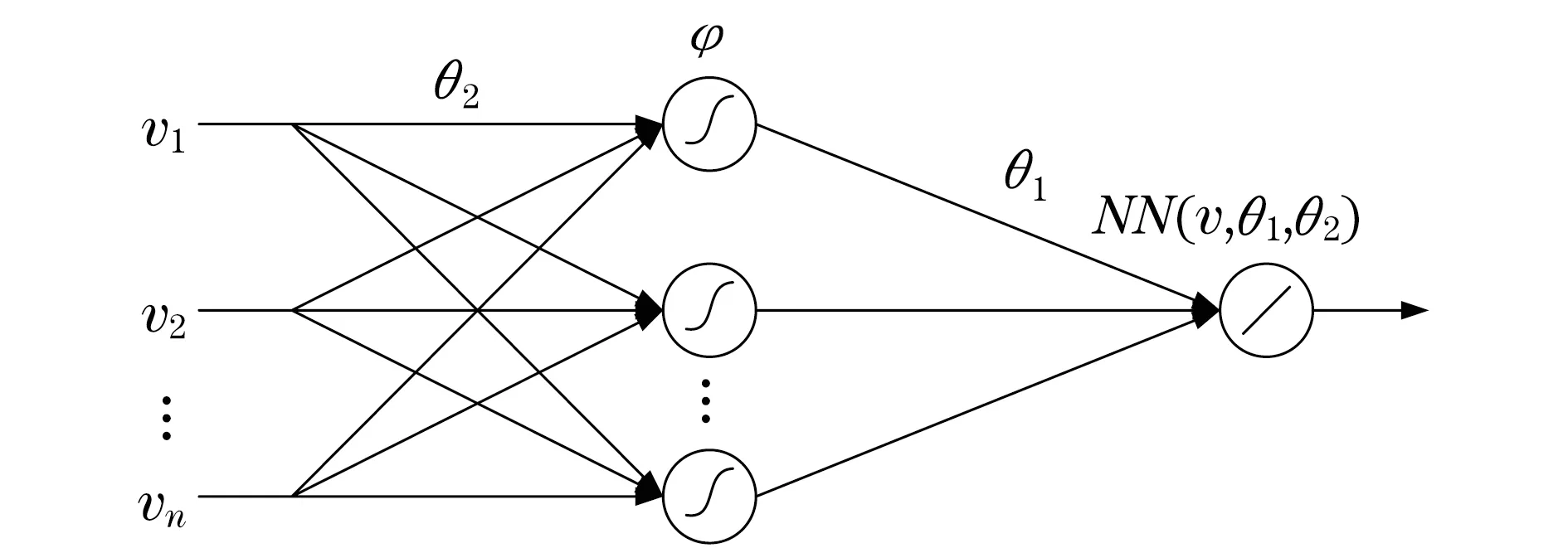
圖2 多層感知器神經網絡Fig.2 Multilayer perceptron neural network

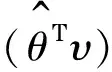
(4)

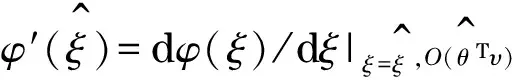
(5)

S形函數φ和它的導數φ′被劃定了界限.有了式(5),我們便可以確定具有泰勒級數的逼近誤差界限為

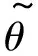
(6)

式中:c1,c2為誤差系數.

3 神經元自適應控制器

3.1控制器分析

神經元自適應控制器的目標是讓機器人末端執行器在具有移動障礙物的情況下,能夠實現軌跡追蹤.所需的軌跡便在操作增廣空間給出的維度為n的變量:

e=Xd-X

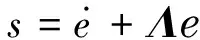
(7)

式中:e為實際運動軌跡與理論運動軌跡誤差;s和xr為機械臂誤差控制函數;Λ為一個正對角矩陣.

在增廣空間X內,所建立的控制法則為

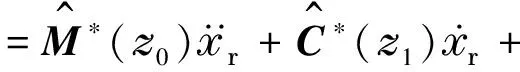
(8)

K>0是一個增益矩陣.之后定義的標志ω,被用來補償逼近誤差.神經元的自適應法則由以下的等式給出:

(9)

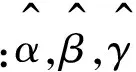
在笛卡爾空間內的控制法則為

(10)

推導得到的最終公式為

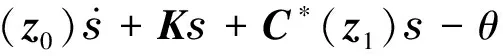
(11)

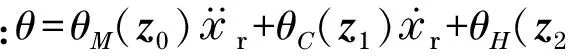
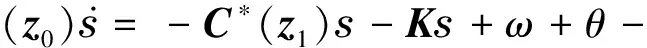
(12)

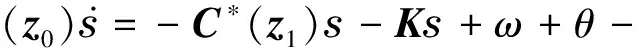
(13)

式中:向量εφ為由于在第一階逼近每一個泰勒級數時由逼近產生的干擾.

通過對矩陣使用弗羅賓尼斯范數,可以得到:

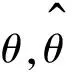
式中:Y{d,o}為兩個有界限的標志;p{1,2}為Λ的正實數函數.

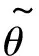
(16)

式中:a{1,2,3}為θmax，Yd，λ，φ的正實數常數函數,也具有使用過的神經網絡θ{M,C,H}的逼近特性.

對由誤差方程(12)定義的系統,有以下的補償項:

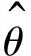
(17)

有

ρω≥a3

(18)

對補償項式(17)而言,針對‖θ‖max的評估是必須的.

3.2穩定性分析

定理1具有由式(9)給定的控制法則、神經元參數自適應法則式(10)和補償項式(17)的在閉環系統中[11]是穩定的.

證明考慮以下候選的李雅普諾夫函數:

由式(9)、式(10)、式(13),可得到該函數對時間的導數為

(19)

因為

(20)

可以寫為

(21)

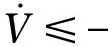
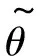
(22)

由式(17)給定的ω的表達式,可得到以下的不等式:

(23)

如果

(24)

最后一個表達式等價于:

(25)

如果滿足以下條件,則上式成立:

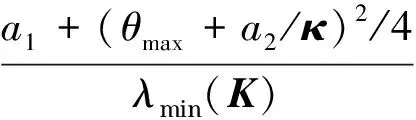
(26)

或者

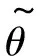
(27)

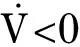
4 仿真結果與分析

用于仿真的機械臂是一個在垂直平面內進化的3自由度機械臂,如圖3所示,長度為l1,l2和l3,所以n=3,m=2.所提議的控制器用于評估在XY平面內對橢圓的輪廓跟蹤.機械臂的第一段被一個移動障礙物所約束,控制器必須能夠避免機械臂與障礙物產生任何碰撞.

障礙物被限制在一個半徑r=0.05 m、中心xo=(x1o,x2o)的圓內.在該圓內,我們可以認為有不止一個障礙物阻礙該機械臂在控制器的幫助下規避與該圓發生碰撞.障礙物的運動方程給出如下:

(28)

式中:fo=0.7 Hz.

所需的軌跡由以下的方程給出,它代表一個橢圓:

(29)

式中:fd=1 Hz.

上式給出了計算障礙物中心和機械臂第一部分l1的距離d的方法.有障礙物的機械臂在圖3中表示.

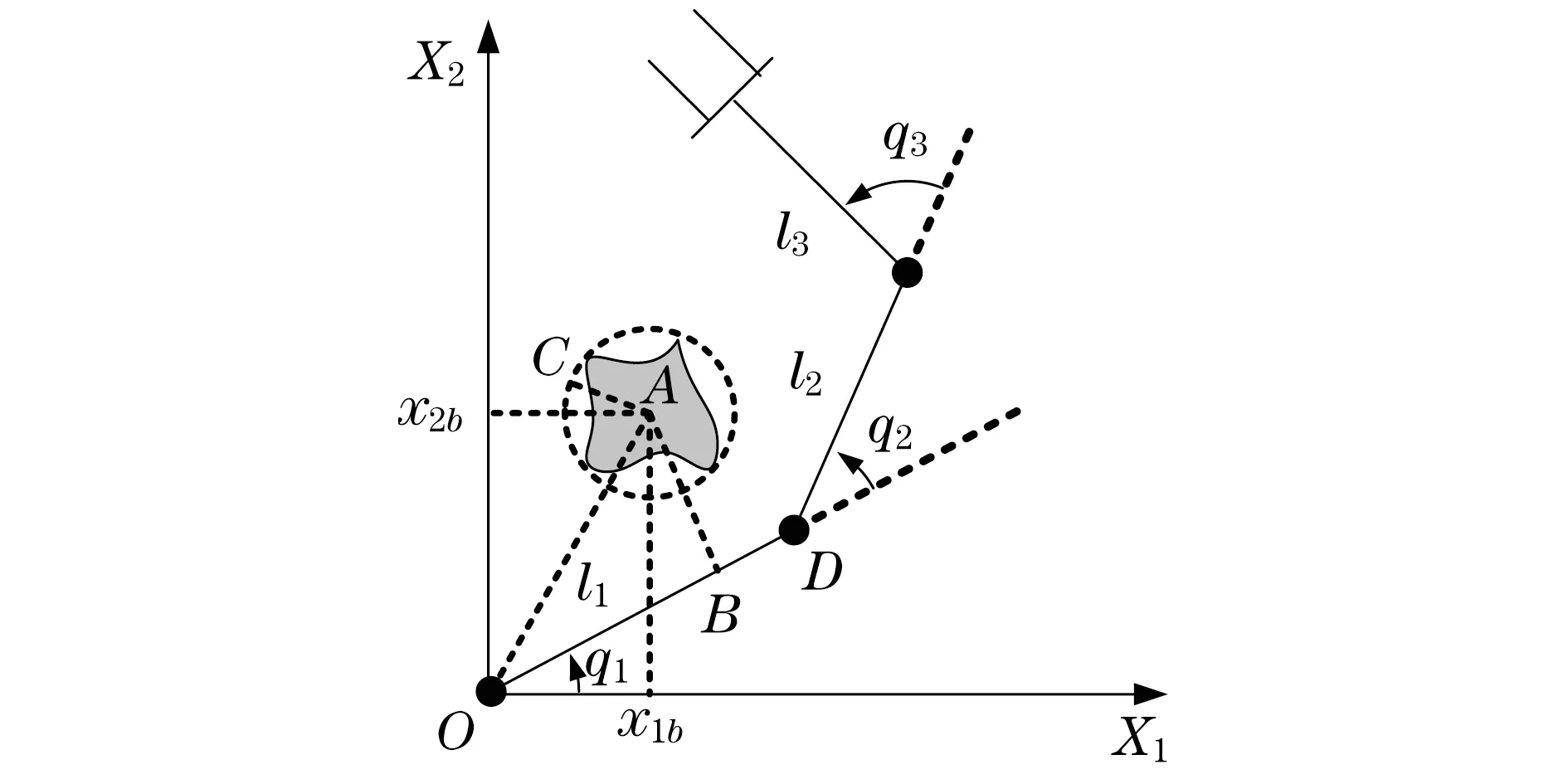
圖3 有1個障礙物的3自由度機械臂Fig.3 Three degrees of freedom manipulatorwith one obstacle

我們定義兩個向量:v1=OA和v2=OD.障礙物的半徑r由AC給出,距離d由AB給出.可以得到以下的公式:

v1·v2=v1v2cos(ψ)

(30)

從這里,可以得到:

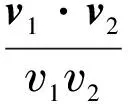
所以可以得到:

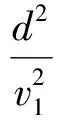
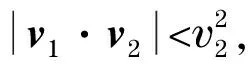
(31)

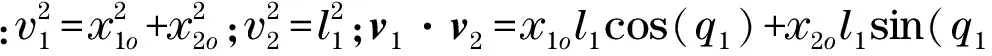
因此,如果|x1ocos(q1)+x2osin(q1)|≤l1,約束不等式為

(32)

將在有障礙物的情況下追蹤所需軌跡,同時最小化關節位移能量作為目的的要優化的判據由以下方程定義:

(33)

式中:α=0.01.

將一個隱藏層中具有5個隱藏細胞的神經網絡和雙曲正切函數用于激活函數.對控制法則參數的選擇如下:

最后采取Matlab/Simulink對機械臂神經網絡軌跡追蹤誤差進行仿真,并與PD追蹤誤差仿真結果進行了對比,仿真結果如圖4所示.

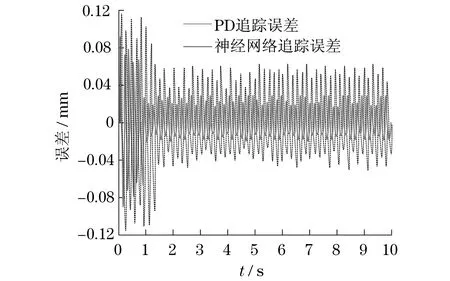
圖4 機械臂軌跡追蹤誤差Fig.4 Tracking error of mechanical arm trajectory

從仿真結果可以看出:PD追蹤誤差較大,最大誤差達到0.11 mm,追蹤誤差自適應時間較長,大約1.2 s;神經網絡追蹤誤差較小,最大誤差達到0.09 mm,追蹤誤差自適應時間較短,大約1.0 s.因此,神經網絡追蹤效果較好.

5 結語

本文介紹了機械臂的動力學,結構特點和障礙物避障,解決了神經元網絡逼近.同時,對自適應控制器的設計和穩定性進行了推導和分析.最后,對神經元網絡追蹤控制器與PD追蹤控制器所產生的誤差進行了仿真和比較.神經元網絡追蹤控制器避開障礙物效果較好,有著重要的工業應用價值,為機械臂運動過程避開障礙物的研究提供了參考.

[1] 王良勇，柴天佑，方正.考慮驅動系統動態的機械手神經網絡控制及應用[J].自動化學報，2009，35(5)：622-626.

WANG L Y,CHAI T Y,FANG Z.Neural network control and application of robotic manipulators including actuator dynamics[J].Acta Automatica Sinica,2009,35(5):622- 626.

[2] WILAMOWSKI B M,COTTON N J,KAYNAK O.Computing gradient vector and Jacobian matrix in arbitrarily connected neural networks[J].IEEE Transactions on Industrial Electronics,2012,55(10):3784-3790.

[3] KUMARA N,PANWARB V,SUKAVANAMC N,et al.Neural network-based nonlinear tracking control of kinematically redundant robot manipulators[J].Mathematical and Computer Modelling,2011,53:1889-1901.

[4] LI Z,YANG Y,LI J.Adaptive motion force control of mobile under-actuated manipulators with dynamics uncertainties by dynamic coupling and output feedback[J].IEEE Transactions on Control Systems Technology,2010,18(5):1068-1079.

[5] BOUKATTAYA M,DAMAKT,JALLOULI M.Robust adaptive control for mobile manipulators[J].International Journal of Automation and Computing,2011,8(1):8-13.

[6] 王紅旗，王慶林.移動機械手運動/力魯棒自適應軌跡跟蹤[J].控制與決策，2010，25(1)：105-109.

WANG H Q,WANG Q L.Motion/force robust and adaptive trajectory tracking of mobile manipulator[J].Control and Decision,2010,25(1):105-109.

[7] XU D,ZHAO D,YI J,et al.Trajectory tracking control of omnidirectional wheeled mobile manipulators:robust neural network-based sliding mode approach[J].IEEE Transactions on Systems,Man,and Cybernetics,2012,39(3):788-799.

[8] 董立紅.基于模糊補償的機械手魯棒自適應模糊控制研究[J].計算機工程與科學，2012，34(1)：169-172.

DONG L H.Research on the robust adaptive fuzzy control of manipulators based on fuzzy compensation[J].Computer Engineering Science,2012,34(1):169-172.

[9] ZHANG L J,LIU J K.Adaptive boundary control for flexible two-link manipulator based on partial differential equation dynamic model[J].IET Control Theory and Applications,2013,7(1):43-51.

[10] 姬偉，程風儀，趙德安.基于改進人工勢場的蘋果采摘機器人機械手避障方法[J].農業機械學報，2013，44(11)：253-258.

JI W,CHENG F Y,ZHAO D A.Obstacle avoidance method of apple harvesting robot manipulator[J].Transactions of the Chinese Society of Agricultural Machinery,2013,44(11):253-258.

[11] KUMAR N,PANWAR V,SUKAVANAM N,et al.Neural network-based nonlinear tracking control of kinematically redundant robot manipulators[J].Mathematical and Computer Modelling,2011,53(3):1890-1899.

Neuralnetworkcontrollerofredundantrobotarmobstacleavoidance

LIUShanchun1,LILi2
(1.Bailie School of Engineering & Technology,Lanzhou City University,Lanzhou 730070,China; 2.Bailie School of Petroleum Engineering,Lanzhou City University,Lanzhou 730070,China)

At present,there are many ways to study robot arm obstacle avoidance controller.Through the analysis of the existing PD controller tracking error,the error is bigger and the effect is poorer.To this,neural network controller is presented,obstacle avoidance tracking error is simulated in the process of movement.To build the dynamic model of robot arm rotating joint obstacle avoidance,in cartesian space extension defines the unknown functions.Using multilayer perceptron neural network approximation method,the closed-loop stability of the neuron adaptive controller system is analyzed.At the same time,the closed-loop stability of the system was proved,nerve parameter adaptive laws is obtained.Combined with concrete example,the robot arm obstacle avoidance neural network controller is simulated.The results show that the robot arm end executor has excellent effect of trajectory tracking under the environment of mobile obstacles.

robot arm; neural network; controller; obstacle avoidance; adaptive laws; simulation

TF 24

： A

： 1672-5581(2017)03-0267-06

甘肅省教育廳基金資助項目(GS[2013]GHB0894)

劉善春(1966—),女,副教授,碩士.E-mail:yuhl201603@sina.com