基于LE和IIN算法的正弦信號頻率估計算法

譚釧章，李宏偉,樊昌周,耿 耿

(1.空軍工程大學信息與導航學院，陜西 西安 710077；2.解放軍95999部隊，北京 100078)

基于LE和IIN算法的正弦信號頻率估計算法

譚釧章1，李宏偉1,樊昌周1,耿 耿2

(1.空軍工程大學信息與導航學院，陜西西安710077；2.解放軍95999部隊，北京100078)

針對信號頻率位于兩個相鄰離散頻率點的中心區域時，迭代插值(Iterative Interpolation Based Algorithm, IIN)算法估計誤差較大，而當信號頻率位于離散頻率點附近時，線性方程(Linear Equation, LE)算法估計誤差較大的問題，提出了一種基于LE和IIN算法的正弦信號頻率估計算法。該算法運用頻譜搬移的思想，首先利用LE算法進行頻率粗估計，然后將原信號往離散頻率點附近頻移，再利用IIN算法進行二次迭代。Monte-Carlo仿真結果表明，該算法頻率估計的均方根誤差在全頻段內逼近克拉美-羅界(Cramer-Rao Lower Bound,CRLB)，精度和穩定性皆優于R-IIN算法、M-LE算法和IIN算法，并且運算量小于IIN算法(二次迭代)和M-LE算法。

頻率估計；頻譜搬移；插值；克拉美-羅界

0 引言

低信噪比條件下正弦信號的頻率估計一直是信號處理領域的經典課題，在雷達和通信等領域有廣泛的應用。國內外許多學者對此有深入的研究。文獻[1]給出了加性復高斯白噪聲中正弦信號頻率的最大似然(Maximum Likelihood, ML)估計，該算法的估計誤差逼近克拉美-羅界(CRLB)，為最優估計，它需要在頻率域進行一維搜索，計算量太大。基于離散傅里葉變換(Discrete Fourier transform, DFT)的頻率估計方法[2]可以利用快速傅里葉變換(Fast Fourier Transform, FFT)實現，因而在工程上得到了廣泛的應用。對截斷的信號進行抽樣離散，然后作FFT變換后，會帶來頻譜泄漏與柵欄效應，通過對信號加窗可以有效減少頻譜泄漏的問題[3-6]。為減小柵欄效應所帶來的估計誤差，文獻[7]提出的Rife算法利用信號頻譜幅度最大的兩根譜線幅度的比值進行插值來估計頻率，高信噪比環境下能有效提高估計精度，在低信噪比條件下容易出現插值方向錯誤[8]。Quinn算法[9-10]利用FFT譜線的相位對相位噪聲有180°的抵抗容限，用幅值最大的三根譜線的復比值的實部進行插值，有效地避免了Rife算法插值方向錯誤的問題。但在低信噪比條件下時，對某些頻率點的估計仍然波動明顯。針對這一問題，Serge提出線性方程(LE)[11-12]算法。該方法對離散正弦信號建立了線性方程模型，較Quinn算法有更強的抗噪性能，在信號頻率位于兩個離散頻率點中心區域時精度較高，在信號頻率點位于離散頻率點附近時估計精度會下降。文獻[13]在Quinn算法的基礎上，利用LE算法來判斷插值方向，提出了基于頻移修正的線性方程頻率估計算法，即M-LE算法，相比Quinn算法在低噪比條件下的估計精度和穩定性有進一步提高。但該算法受Quinn算法在信號頻率越靠近離散頻率點時估計誤差會變大的限制，在全頻段內估計性能不穩定，出現波動。Aboutanios提出一種迭代插值(IIN)算法[14-15]，通過兩次以上的迭代使得MSE逼近CRLB。該算法在信號頻率位于量化頻率點附近時精度較高，否則要經過多次迭代來減小估計誤差，而多次迭代會產生巨大的運算量。文獻[16]結合Rife算法在信號頻率位于兩個相鄰量化頻率點的中心區域時精度較高和IIN算法在信號頻率位于量化頻率點附近時精度較高的優點，提出了R-IIN算法，在高信噪比條件下有良好的估計性能。但是Rife算法在低信噪比條件下易出現插值方向錯誤，因此R-IIN算法在低信噪比條件下估計誤差較大，在低信噪比條件下進行頻率估計時精度下降。

本文針對LE算法和IIN算法的估計誤差依信號頻率而變化且波動較大的問題，結合兩種算法的優點，提出了基于LE和IIN算法的正弦信號頻率估計算法。

1 LE算法和IIN算法原理

1.1 信號模型

加性高斯白噪聲污染的復正弦信號模型可表示為：

x(n)=Aej(2πfn+φ)+w(n),n=0,1,…,N-1

(1)

其中，A、f、φ分別為信號的振幅、歸一化頻率和初始相位，N為信號序列長度。w(n)為均值為零，方差為σ2的復高斯白噪聲序列。對x(n)作FFT，得到其傅里葉變換：

(2)

其中，W(k)為w(n)的傅里葉變換。其頻譜圖分辨率為Δf-fs/N，fs為采樣頻率。設k=k0時X(k)幅度最大，當信號頻率f正好為Δf的整數倍時，真實頻率與最大譜線位置重合，估計值不會出現偏差。在實際中出現這種情況的概率很小，更常見的是信號頻率位于最大譜線位置與次大譜線位置之間，不失一般性，信號的真實頻率可表示為:

f=(k0+δ)×Δf；δ∈[-0.5,0.5]

(3)

因此，插值類算法可以分兩步進行。第一步，粗估計：對信號序列作FFT得到最大幅度譜線對應位置k0(整數)；第二步，精估計：利用插值算法對偏差δ(分數)進行精確估計，最后根據式(3)得出頻率估計值。

1.2LE算法原理

在無噪聲污染環境下時，復正弦信號模型由式(1)可進一步表示為[11-12]：

s(n)=Aλm

(4)

其中，λ=ejω，A為信號幅度。 對s(n)作DFT得到：

(5)

式(5)中，WN=e-j2π/N，p=A(1-λN)。等式兩邊同時乘以分母，式(5)變形為：

(6)

在噪聲環境下，式(1)和式(2)可由式(4)、式(5)表示為：

x(n)=s(n)+ω(n)

(7)

X(k)=S(k)+ψ(k)

(8)

為區分W(k)與WN，將W(k)用ψ(k)代替(如式(8)中所示)。式(7)、式(8)直接代入式(6)得到：

(9)

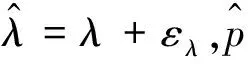
(10)

(11)

(12)

(13)

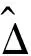
1.3IIN算法原理

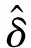
1)迭代一：

(14)

(15)

2)迭代二：

(16)

(17)

3)

(18)

IIN算法是把信號的頻譜往靠近|δ|=0的方向進行頻譜搬移，即往離散頻率點附近頻移。當信號頻率t位于離散頻率點附近時，X0.5與X-0.5的實部值大小十分接近，同時值較大，受噪聲影響較小，此時IIN算法的估計精度較高。當信號頻率f位于兩個離散頻率點的中心區域時，X0.5與X-0.5兩者之中遠離Xk0的實部值較小，受噪聲干擾較大，算法估計的精度下降，此時需要多次迭代才能逼近CRLB。

2 基于LE和IIN算法的正弦信號頻率估計算法

由以上分析可知：IIN算法在信號頻率位于離散頻率點附近時估計精度較高，位于兩離散頻率點中心區域時，受噪聲影響估計精度下降。而LE算法在低信噪比條件下具有良好的抗噪聲性能，在全頻段內性能穩定，且在兩個離散頻率點中心區域時具有較高的估計精度[11]。

因此，對原始信號進行離散化處理之后，首先用LE算法來判斷插值方向，確定插值方向的準則為：

(19)

綜上所述，基于LE和IIN算法的正弦信號頻率估計算法實現步驟如下：

1)對信號作FFT，得到最大譜線位置；

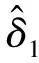
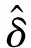
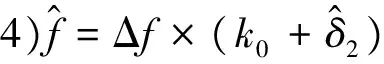
3 實驗仿真和計算量分析

為了驗證基于LE和IIN算法的正弦信號頻率估計算法的穩定性與估計精度，利用Monte-Carlo模擬實驗的方法對算法進行仿真，并與M-LE算法[13]、IIN算法[14]和 R-IIN算法[16]進行對比。仿真實驗分為兩個部分：第一部分是各算法在信號頻率位于兩個離散頻率點之間不同位置時的估計誤差的對比，實驗結果采用均方誤差(Mean Square Error, MSE)與克拉美-羅界的比值，即MSE/CRLB來度量；第二部分分析了各算法在不同信噪比條件下的估計誤差，實驗結果為MSE。定義信噪比SNR=A2/σ2，在正弦信號的幅度和初始相位都未知的情況下，頻率估計的CRLB為[1]：

(22)

3.1 實驗仿真與結果分析

仿真條件1): 采樣頻率fs=1 MHz，采樣點數N=256，信號頻率f=Δf(20+δ)，其中δ∈[-0.5,0.5]，區間間隔為0.05。分別在SNR為10 dB、和-6 dB的條件下，對每個頻點處做1 000次Monte-Carlo仿真，得到其性能曲線分別如下圖 1 (a)和圖1 (b)所示。

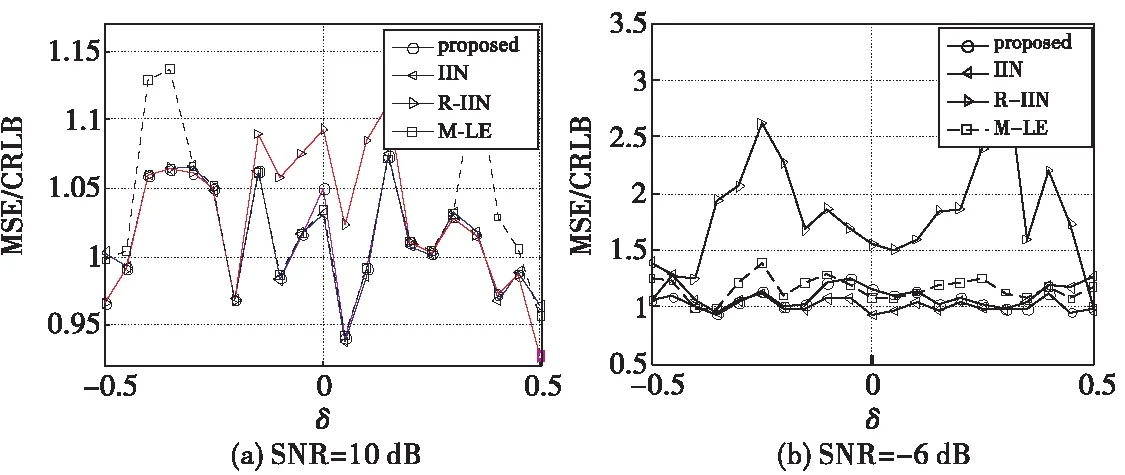
圖1 不同信號頻率處各算法MSE/CRLB值Fig.1 MSE/CRLBof each algorithm

由圖1仿真結果可知，在信噪比較高(SNR=10 dB)的情況下，由于R-IIN和M-LE分別是在Rife算法和Quinn算法的基礎之上的改進，受到Rife算法和Quinn算法在全頻段內不穩定的限制，部分頻率點的誤差較大，基于LE和IIN算法的正弦信號頻率估計算法的性能曲線幾乎與IIN算法的性能曲線重合，算法在全頻段內的穩定性和整體的估計精度都明顯優于R-IIN和M-LE算法；在信噪比較低(SNR=-6 dB)的情況下，R-IIN算法的估計誤差變得比較大，達到了2.5倍以上CRLB。M-LE算法的估計誤差波動明顯，MSE整體在1.4倍CRLB以下，IIN算法在|δ|→0時MSE逐步變大，整體在1.4倍CRLB以下。而基于LE和IIN算法的正弦信號頻率估計算法在全頻段內性能都比較穩定，均方誤差(MSE)在1.2倍CRLB以下，優于R-IIN算法、M-LE算法和IIN算法。

仿真條件2): 采樣頻率fs=1 MHz，采樣點數N=256，SNR∈[-8,2]，區間間隔為0.5，分別在信號頻率f=Δf(20+0.05)和f=Δf(20+0.45)時，在每個信噪比條件下做1 000次Monte-Carlo仿真實驗，得出MSE性能曲線如下圖2(a)和圖2 (b)所示。

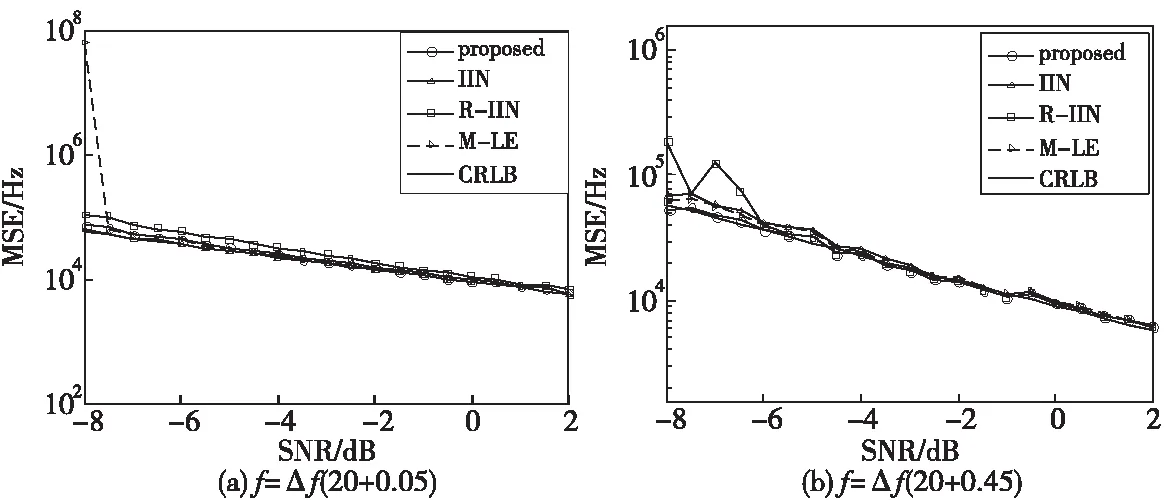
圖2 不同信噪比條件下各算法估計性能Fig.2 The comparison of MSE in different SNR

由圖2仿真結果可知M-LE算法在f=Δf(20+0.05)頻點處信噪比門限高于另外三種算法，信噪比達到-7 dB以下時，算法失效。R-IIN算法的MSE明顯高于另外三種算法。當f=Δf(20+0.45)時,在信噪比達到-6 dB的條件下，R-IIN算法波動較大,估計精度下降。而基于LE和IIN算法的正弦信號頻率估計算法性能始終表現穩定。當|δ|→0時，其MSE大小與IIN算法相當 ，當|δ|→0.5時，其MSE小于IIN算法，更加逼近CRLB。

3.2 計算量分析

作一次N點的FFT需要(N/2)log2N次復數乘法和Nlog2N次復數加法。此外，基于LE和IIN算法的正弦信號頻率估計算法在判斷插值方向時要增加兩次復數乘法和兩次復數加法。進行二次迭代計算X±0.5時增加2N次復數乘法2(N-1)次復數加法。各算法運算量比較如表1所示。

表1 各算法運算量分析

由表1分析可知，基于LE和IIN算法的正弦信號頻率估計算法的運算量小于M-LE算法和IIN算法(二次迭代)，比R-IIN算法只多兩次復數乘法和兩次復數加法。因此，基于LE和IIN算法的正弦信號頻率估計算法在不顯著增加運算量的情況下，提高了估計精度和穩定性，整體計算量較小，便于硬件實現。

4 結論

本文分析了LE算法和IIN算法的特點，并結合兩種算法提出了基于LE和IIN算法的正弦信號頻率估計算法。該算法既利用了LE算法在信號頻率位于兩離散頻率點中心區域時精度較高和抗噪性能良好的優點，避免了插值方向錯誤的問題，又發揮了IIN算法在信號頻率位于離散頻率點附近時精度較高的優點。實驗仿真結果表明，基于LE和IIN算法的正弦信號頻率估計算法在全頻段內性能的穩定性和精度整體優于R-IIN算法、M-LE算法和IIN算法，在保證運算量較小的同時有效地提高了估計精度和穩定性，適用于信號頻率的實時估計且精度要求較高的場合。

[1]Rife D C, Boorstyn R R. Single-tone parameter estimation from discrete-time observations[J]. IEEE Transactions on Information Theory, 1974, 20(5):591-598.

[2]Palmer L C. Coarse frequency estimation using the discrete fourier transform[J]. IEEE Transactions on Information Theory, 1974, IT-20(1):104-109.

[3]Duda K. DFT interpolation algorithm for Kaiser-Bessel and Dolph-Chebyshev windows[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(3): 784-790.

[4]Belega D, Petri D. Frequency estimation by two-or three-point interpolated Fourier algorithms based on cosine windows[J]. Signal Processing, 2015, 117: 115-125.

[5]Candan ?. Fine resolution frequency estimation from three DFT samples: Case of windowed data[J]. Signal Processing, 2015, 114: 245-250.

[6]Werner K J, Germain F G. Sinusoidal parameter estimation using quadratic interpolation around power-scaled magnitude spectrum peaks[J]. Applied Sciences, 2016, 6(10): 306.

[7]Rife D C, Vincent G A. Use of the discrete fourier transform in the measurement of frequencies and levels of tones[J]. Bell Labs Technical Journal, 1970, 49(2):197-228.

[8]齊國清. 幾種基于FFT的頻率估計方法精度分析[J]. 振動工程學報, 2006, 19(1):86-92.

[9]Quinn B G. Estimating frequency by interpolation using Fourier coefficients[J]. Signal Processing IEEE Transactions on, 1994, 42(5):1264-1268.

[10]Quinn B G. Estimation of frequency, amplitude, and phase from the DFT of a time series[J]. IEEE Transactions on Signal Processing, 1997, 45(3):814-817.

[11]Provencher S. Estimation of complex single-tone parameters in the DFT domain[J]. IEEE Transactions on Signal Processing, 2010, 58(7):3879-3883.

[12]Provencher S. Parameters estimation of complex multitone signal in the DFT domain[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3001-3012.

[13]李夏, 郭英, 張坤峰,等. 基于頻移修正的線性方程頻率估計算法[J]. 探測與控制學報, 2015,37(4):66-71.

[14]Aboutanios E, Mulgrew B. Iterative frequency estimation by interpolation on Fourier coefficients[J]. IEEE Transactions on Signal Processing, 2005, 53(4):1237-1242.

[15]Aboutanios E. Estimating the parameters of sinusoids and decaying sinusoids in noise[J]. IEEE Instrumentation & Measurement Magazine, 2011, 2(14): 8-14.

[16]周龍健, 羅景青, 房明星. 基于IIN算法和Rife算法的正弦波頻率估計算法[J]. 數據采集與處理, 2013, 28(6):839-842.

FrequencyEstimatorofSinusoidSignalBasedonLEandIINAlgorithm

TAN Chuanzhang1, LI Hongwei1，FAN Changzhou1,GENG Geng2

(1. Information and Navigation College, Air Force Engineering University, Xi’an 710077, China; 2. Unit 95999 of PLA, Beijing 100078, China)

Aiming at the problem that when the frequency locates in the central region of two adjacent discrete frequency points, the variance of iterative interpolation (IIN) based estimator becomes larger and the estimation precision of linear equation (LE) algorithm decrease when the frequency is near to the discrete frequency points, a new algorithm which based on LE and IIN algorithm was proposed in this paper. Firstly, a coarse frequency was estimated by the LE algorithm. Then move the original signal to the discrete frequency point via frequency shift modification. Finally, the second iteration of IIN algorithm was used to get a fine signal frequency estimate. Monte-Carlo simulation showed that the root mean square error (RMSE) approached to Cramer-Rao lower bound(CRLB) throughout whole frequency range. The performance of the proposed algorithm was better than R-IIN algorithm, M-LE algorithm and IIN algorithm both in accuracy and stability, and the computation was smaller than IIN algorithm(two iterations) and M-LE algorithm.

frequency estimation; frequency shift modification; interpolation; Cramer-Rao lower bound

2017-01-12

:國家自然科學基金項目資助(61571457)

:譚釧章(1993—)，男，湖南湘潭人，碩士研究生，研究方向：雷達信號處理。E-mail:jzscion@163.com。

TN911.6

：A

：1008-1194(2017)04-0119-05